基于灰色理论预测模型的商业综合体项目基坑形变监测研究

摘要

由于基坑形变成因过多，导致安全监测难度增加，因此提出了一种基于灰色理论预测模型的基坑形变监测方法。首先建立灰色理论预测模型和一阶线性动态微分方程，并利用样本数据和基坑形变参数的时间和状态序列计算响应函数，将函数值转换为测试点形式，求解每个点的向量和权重参数，将其作为模型的初始参照。其次建立监测模型的初始序列，采用最小二乘积算法生成监测均值方程，计算背景值、灰度值以及邻近系数，比较三者的线性关系给出监测点的残差条件序列，并求得监测模型可实施条件，完成基坑形变的有效监测。以远洋新光商业综合体项目为例进行了实验验证，结果表明，灰色理论预测模型的监测精准度较高，误差较小，实用性强。

关键词

灰色理论预测模型;基坑形变;响应函数;状态序列;监测均值方程

中图分类号：TP183；TU433"" 文献标志码：A"" 文章编号：1004-0366（2024）06-0025-06

近年来，随着社会的不断进步与发展，城市基础设施建设越来越完善，同时人们对空间的需求也逐渐扩增。为满足人们日益增长的建设需求，建筑领域的重点已开始转向地下建筑。然而，基坑工程的周围环境和地质条件通常相对复杂，存在较多的不确定性因素，导致施工难度与施工复杂性大幅度增加。因此，在开展基坑工作时，需要对地下环境和基坑形变进行监测。在工程的前期阶段，通过监测可得到实时施工数据，按照数据可制定开坑工作计划。通过这种方式可及时对后期施工方案进行调整优化，并对可能发生的危险进行预判，大幅度提升了工程的质量和安全性。

在基坑形变监测研究中，文献［1］中提出了一种基于Kalman滤波的神经网络预测模型，并在深基坑沉降监测中应用。由于预测环境中存在许多因素的影响，不可避免地会出现预测残差问题。为解决这个问题，研究者将Kalman滤波与预测模型相结合，在对数据进行去噪处理后重新建立残差模型，然后将现场参数代入残差模型，并在模型中查找符合基坑形变的监测点，以此完成形变监测，但该方法在实际应用中的可行性不强，无法有效地融合去噪和预测这两个步骤，导致监测误差较大。文献［2］中采用了一种基于差异时距非齐次灰色模型的基坑沉降变形预测方法，建立了差异时距非齐次模型，将采集到的基坑不同时间段的具体数据代入模型，求解参数的线性变化趋势，与实时监测数据作对比，但该方法监测精度较低。文献［3］中采用优化灰色GOM（1，1）模型与BP神经网络组合预测，GOM（1，1）模型是在GM（1，1）模型原理上对其参数进行优化，使拟合值接近观测值，BP神经网络具有较强的非线性数据处理能力，优化组合模型结合二者优点应用于基坑沉降监测，但该方法所需的运算量较大，实际应用效果不强。

综合上述问题，本次研究提出了灰色理论预测模型，并将其应用在远洋新光商业综合体项目基坑形变监测中。灰色理论预测模型以远洋新光商业综合体项目的历年真实数据为基础，明确预测基坑形变随时间变化的响应函数，求解函数得到响应程度最高的参数值，并将其作为后续监测点的残差参照数据，从而实现高精准对比。将预测模型合理应用在监测算法中，采集基坑形变现场参数，针对不同位置设置监测点，监测点的距离间隔需与预测函数序列相对应，实现一一对比分析。通过这种方式提升了监测结果的精准度并尽可能减小监测误差。最终通过灰度概念来划分监测点的残差等级，并对误差较大的点进行合理约束。灰色理论预测模型监测方法适用于多种环境，受背景值影响较小，适应能力较强，具有较好的应用价值。

1 灰色理论预测模型建立

通常情况下，预测模型在监测过程中起到一定的参照作用。预先对远洋新光商业综合体项目基坑形变的监测点的数据序列进行预测，可提前获取预测结果，并根据结果设定合理的监测指标，可大幅降低误差值并提高精准度。建立灰色理论预测模型［3］GM（1，1），当预测模型中N=1时（N为时间序列值），代表测试预测结果属于一阶线性动态微分方程。

设定样本数据序列为

X（0）=（x（0）（1），x（0）（2），∧，x（0）（n））， （1）

其中：x（0）为初始样本状态数值;n为样本数量。

推导得出上一时间点的基坑形变的样本数据序列为

X（-1）=（x（-1）（1），x（-1）（2），∧，x（-1）（n）），（2）

其中：x（-1）为上一时间点的样本状态数值，令Z（i）i（k）=0.5×（x（i）i（k），x（i）i（k-1），k=2，3，∧，n），得到在预测模型GM（1，1）下，数据样本状态和时间序列参数值之间的对应关系，其表达式为

x（i）i（k）+az（i）i=b， （3）

其中：a、b分别为响应系数;k为预测次数;z（i）i为在i时间点的数据响应参数［4］。通过上述分析得到预测模型中第2、3、4、5时间点下的预测矩阵为

Y=x（0）i（2）x（0）i（3）x（0）i（4）x（0）i（5）， B=-z（1）i（2），1-z（1）i（3），1-z（1）i（4），1-z（1）i（5），1，ai=（ai，bi）T，（4）

则有

ai=（BTB）-1BY， （5）

其中：ai、bi分别为预测事件i（基坑形变）的响应函数;T为预测周期;B、Y分别为预测样本状态矩阵和响应参数矩阵。当事件响应序列与预测序列相等时，代表此时预测点的数值与实际数值之间贴近程度最高。基坑形变事件响应序列函数为

x″（i）i（t）=x（1）i（1）-biaie-α+biai， （6）

其中：e-α为约束事件响应的时间参数;t为序列值。由此推导得到与其相对应的预测函数表达［6］：

x（1）i（t+1）=x（1）i（t+1）-x（1）i（t）=（1-e-α）·

x（0）i-biaie-α+biai， t=1，2，…，5（7）

通过上述公式得到基坑形变数据序列的最终预测结果，并将预测值作为后续基坑形变监测的参照，同时采用预测函数对每个监测点进行概念分类［7］，以最大程度提高监测精准度。灰色预测模型的概念分类如表1所列。

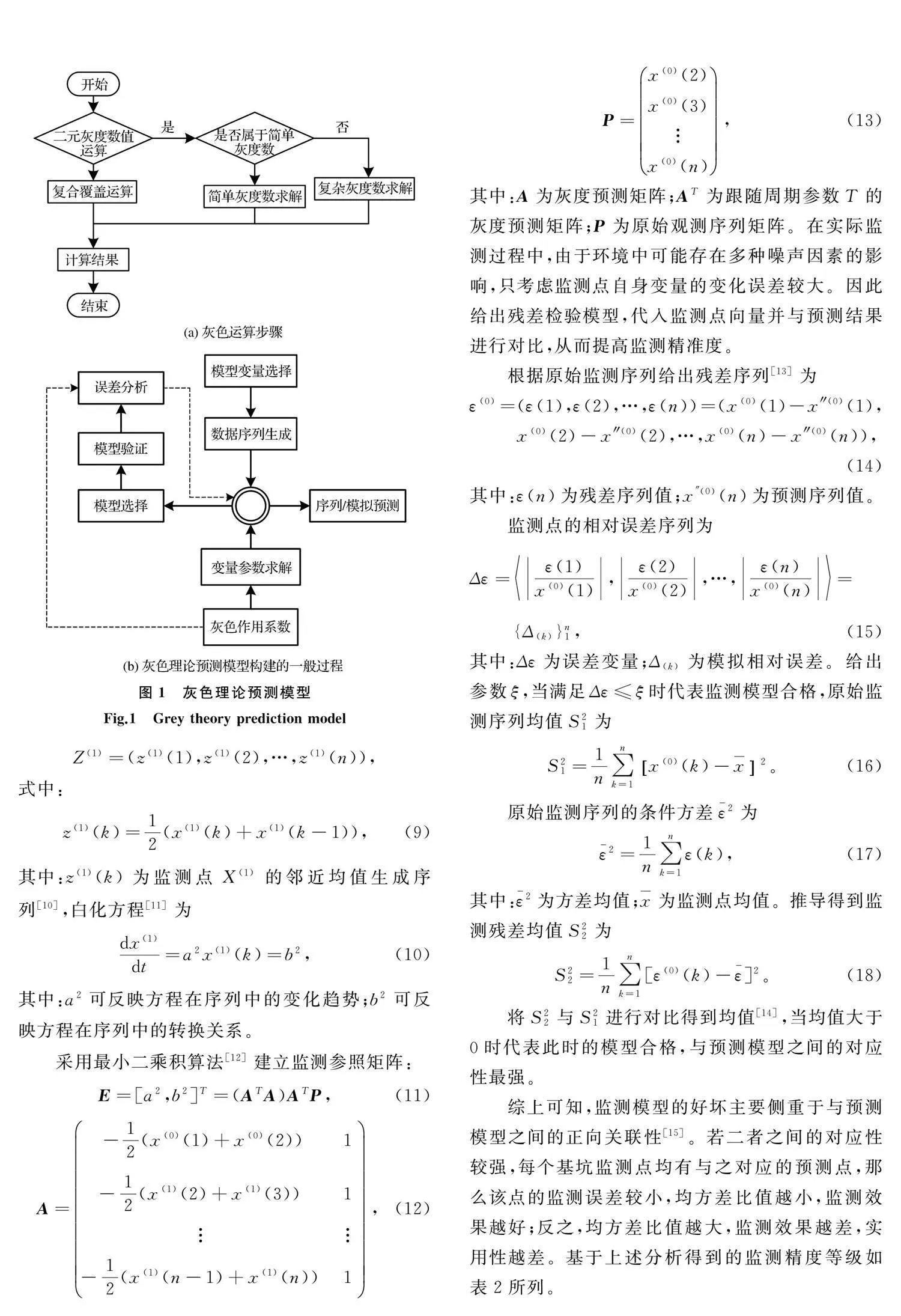
表1中显示“灰色”的概念主要处于黑色和白色之间，其代表一种模糊不定［8］的概念形式。灰色预测模型可针对不确定点进行有效预测，降低监测误差，预测模型示意图如图1所示。

2 灰色理论预测模型在基坑形变监测中的应用

以上述过程建立的灰色理论预测模型为基础，定义监测点原始观测序列，将远洋新光商业综合体项目基坑参数代入，求解基坑形变事件的预测结果。假设在基坑形变监测中，某一监测点存在n个非负的原始观测序列X（0）=（x（0）（1），x（0）（2），…，x（0）（n）），即预测序列［9］。设该序列值的原始形态为

x（0）（k）+ax（0）（k）=b， （8）

设X（0），X（1）满足

Z（1）=（z（1）（1），z（1）（2），…，z（1）（n）），

式中：

z（1）（k）=12（x（1）（k）+x（1）（k-1））， （9）

其中：z（1）（k）为监测点X（1）的邻近均值生成序列［10］，白化方程［11］为

dx（1）dt=a2x（1）（k）=b2， （10）

其中：a2可反映方程在序列中的变化趋势;b2可反映方程在序列中的转换关系。

采用最小二乘积算法［12］建立监测参照矩阵：

E=［a2，b2］T=（ATA）ATP， （11）

A=-12（x（0）（1）+x（0）（2））1

-12（x（1）（2）+x（1）（3））1

-12（x（1）（n-1）+x（1）（n））1，（12）

P=x（0）（2）x（0）（3）x（0）（n）， （13）

其中：A为灰度预测矩阵;AT为跟随周期参数T的灰度预测矩阵;P为原始观测序列矩阵。在实际监测过程中，由于环境中可能存在多种噪声因素的影响，只考虑监测点自身变量的变化误差较大。因此给出残差检验模型，代入监测点向量并与预测结果进行对比，从而提高监测精准度。

根据原始监测序列给出残差序列［13］为

ε（0）=（ε（1），ε（2），…，ε（n））=（x（0）（1）-x″（0）（1），x（0）（2）-x″（0）（2），…，x（0）（n）-x″（0）（n）），（14）

其中：ε（n）为残差序列值;x″（0）（n）为预测序列值。

监测点的相对误差序列为

Δε=〈ε（1）x（0）（1），ε（2）x（0）（2），…，ε（n）x（0）（n）〉={Δ（k）}n1，（15）

其中：Δε为误差变量;Δ（k）为模拟相对误差。给出参数ξ，当满足Δε≤ξ时代表监测模型合格，原始监测序列均值S21为

S21=1n∑nk=1x（0）（k）-2。 （16）

原始监测序列的条件方差2为

2=1n∑nk=1ε（k）， （17）

其中：2为方差均值;为监测点均值。推导得到监测残差均值S22为

S22=1n∑nk=1［ε（0）（k）-］2。 （18）

将S22与S21进行对比得到均值［14］，当均值大于0时代表此时的模型合格，与预测模型之间的对应性最强。

综上可知，监测模型的好坏主要侧重于与预测模型之间的正向关联性［15］。若二者之间的对应性较强，每个基坑监测点均有与之对应的预测点，那么该点的监测误差较小，均方差比值越小，监测效果越好;反之，均方差比值越大，监测效果越差，实用性越差。基于上述分析得到的监测精度等级如表2所列。

采用灰色理论预测模型能够对基坑形变进行准确的监测和预测，具有较高的监测精度和较小的误差。基坑形变受多个因素影响，而该方法能够综合考虑样本数据和基坑形变参数的时间和状态序列，将多个因素纳入模型中进行监测。同时该方法建立了监测模型的初始序列，并通过最小二乘积算法生成监测均值方程，可根据实际情况灵活调整和优化模型参数以提高实用性。传统的形变监测方法多采用数学统计方法，而该方法创新性地引入了灰色理论预测模型和一阶线性动态微分方程，使得监测方法更加科学和准确。该方法通过计算响应函数、转化为测试点形式和求解向量和权重参数等步骤，建立了完善的监测流程，并对监测模型的可实施条件进行研究，保证了基坑形变监测的可行性和有效性。综上所述，基于灰色理论预测模型的远洋新光商业综合体项目基坑形变监测方法具有高精度、多因素考虑、灵活性和实用性强等优势和特点，并通过引入灰色理论预测模型和一阶线性动态微分方程来进行监测，提高了监测方法的科学性和准确性。

3 性能测试

3.1 测试环境

为验证本次研究提出的灰色理论预测模型在远洋新光商业综合体项目基坑形变监测中的应用效果，选择近期远洋综合体项目内的一项工程进行实验。该工程是对某车站的地下深基坑进行形变监测。基坑形变的成因较多，如长期损耗、自然因素以及人为因素等。为了能更好地验证灰色理论预测模型在监测中应用的有效性，需要动态序列、残差值以及背景值3个指标验证。

在观测序列中选择12期数据进行监测，并将监测值与实测值进行对比。动态序列、残差值以及背景值的指标概念为：动态序列采用远洋新光商业综合体项目基坑形变的实时监测数据序列，将监测结果与实测序列中的数值进行对比;残差值是在相同条件下，算法监测之间的残差对比;背景值是指除基坑形变的相关参数外，其余背景数值。

3.2 基坑形变监测的应用结果

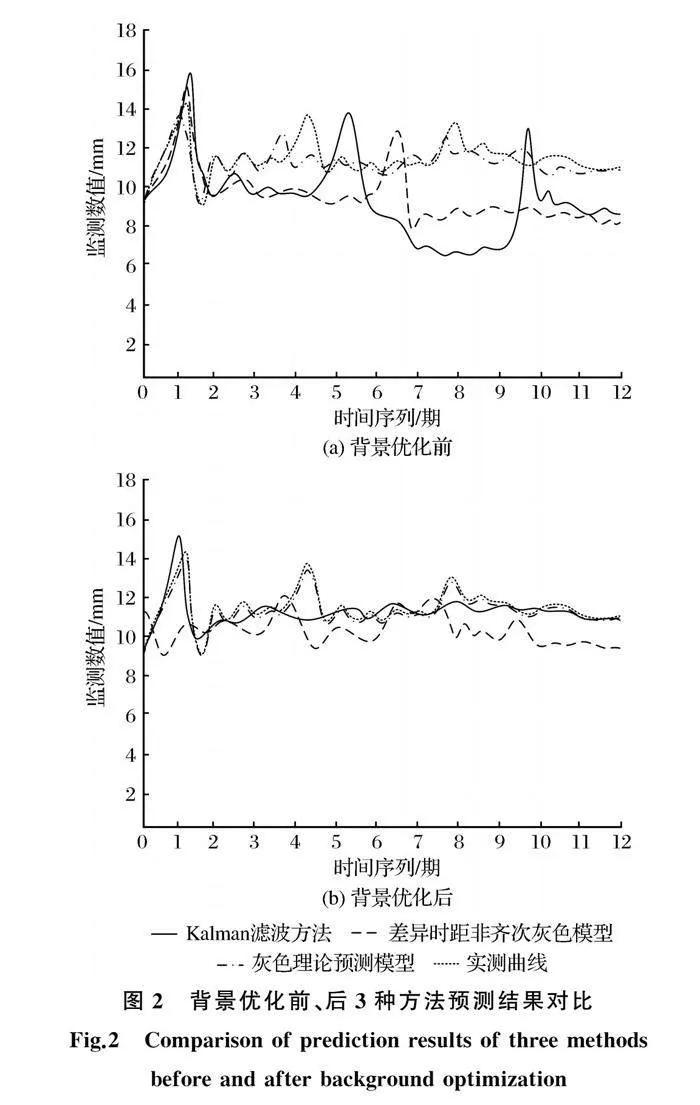
为进一步提高结果的可信性，将基于Kalman滤波的神经网络模型在深基坑沉降监测中的应用和差异时距非齐次灰色模型的基坑沉降变形预测进行对照。背景优化是指去除环境中的背景噪声值，只考虑基坑自然形变参数，给出背景优化前、后的测试条件，实验结果如图2所示。

由图2对比可知，背景优化前、后的灰色理论预测模型监测结果都是最准确的，与实测值之间差距较小，即使在背景值较为杂乱，存在噪声的情况下也能保证精度，说明灰色理论预测模型监测准确性高。然而，另外两种方法的监测值与实测值差距较大，说明监测算法误差较大，实用效果较差。该现象的主要原因是预测模型存在一定的计算误差，导致监测结果受到影响，其算法适应能力和鲁棒性较差。

3.3 基于残差值比对的实验结果

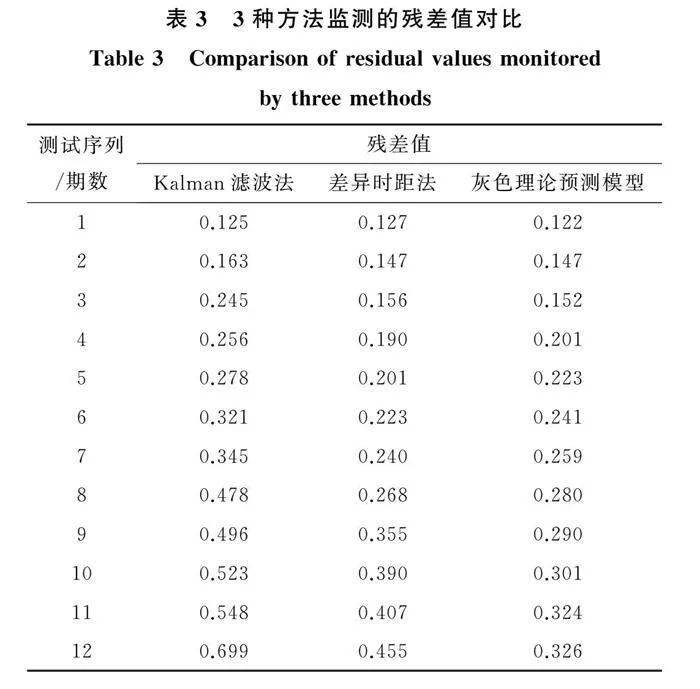
结合图2中的监测结果计算残差值，实验结果如表3所列。

表3中显示的灰色理论预测模型的残差值最小，数值变化最为稳定，说明灰色理论预测模型监测精准度较高，可实现基坑形变高效监测。

4 结论

针对基建工程的高质量和高安全需求，本次研究提出了一种基于灰色理论预测模型的远洋新光商业综合体项目基坑形变监测方法。由于预测模型与监测模型之间存在一定关联，因此预先建立预测模型，并采用动态线性序列分析法来计算基坑形变事件的响应序列函数，按照响应值来进行预测并求得预测结果，然后将该值作为后续监测函数的初始参照值，从而大幅提高了监测的精准度。监测模型以预测结果为基础，计算在不同时间和位置基坑形变的残差数值，并将残差值与预测值进行对比，降低监测误差。实验结果表明，灰色理论预测模型监测精准度较高，实用效果好。

参考文献：

［1］ 牛全福，李月锋，张曼，等.基于Kalman滤波的ARIMA-NAR神经网络模型在深基坑沉降监测中的应用［J］.兰州理工大学学报，2022，48（2）：131-135.

［2］ 邓林义.差异时距非齐次灰色模型的建立及基坑沉降变形预测应用［J］.四川建筑科学研究，2022，48（3）：79-85.

［3］ 李明，孙欣，赵伟，等.优化灰色BP神经网络组合模型在基坑沉降监测中的应用［J］.吉林建筑大学学报，2023，40（5）：25-30.

［4］ 田雪，吴文青，马新.双曲正弦驱动项的新型灰色预测模型及其在能源消费中的应用［J］.数学的实践与认识，2021，51（24）：117-125.

［5］ 袁志明，李沛鸿，刘小生.顾及邻近点的改进PSO-SVM模型在基坑沉降预测的应用研究［J］.大地测量与地球动力学，2021，41（3）：313-318.

［6］ 包龙生，冯元东，包宇扬，等.GM-BP组合预测模型在桥梁施工监控中的应用［J］.沈阳建筑大学学报（自然科学版），2022，38（2）：296-305.

［7］ 徐士祺，殷彦龙，杜胤，等.改进灰色模型在含蜡原油管道蜡沉积厚度预测中的应用研究［J］.安全与环境学报，2022，22（6）：3041-3049.

［8］ 洪宇超，钱建固，叶源新，等.基于时空关联特征的CNN-LSTM模型在基坑工程变形预测中的应用［J］.岩土工程学报，2021，43（增刊2）：108-111.

［9］ 刘思峰.灰色系统理论的发展及其在自然科学和工程技术领域的广泛应用［J］.南京航空航天大学学报，2022，54（5）：851-866.

［10］ 唐林俊，宁晓骏，李杨，等.基于灰色理论与BP神经网络的隧道围岩变形预测［J］.工业安全与环保，2021，47（10）：88-93.

［11］ 杨景尧，刘美红，宋晓磊.基于灰色系统理论的刷式密封磨损量的预测方法［J］.宇航材料工艺，2022，52（6）：83-86.

［12］ 叶笛，刘明艳，俞绍林，等.基于综合加权-灰色关联模型的基坑开挖临空面稳定性分析［J］.建筑结构，2022，52（增刊1）：2497-2503.

［13］ 蒋玉婷，程世娟，殷泽凯.基于灰色预测理论的加速试验数据可靠性评估模型［J］.机械强度，2021，43（1）：159-162.

［14］ 王皓晨，李飒，林澜，等.基于BP模型的基坑开挖引起邻近隧道变形预测［J］.地下空间与工程学报，2021，17（增刊2）：832-839，847.

［15］ 阳建中，陈慧蓉，刘志先，等.信息熵和多因素灰色系统模型在碳排放的分析与预测［J］.中南民族大学学报（自然科学版），2022，41（1）：123-128.

Research on deformation monitoring of foundation pit in commercial

complex projects based on grey theory prediction model

Lu Guo，WANG Bo，LI Jiang

（Construction Comprehensive Survey and Design Institute Company Limited，Beijing 100000，China）

Abstract

Due to the excessive formation of foundation pits， the difficulty of safety monitoring has increased. A deformation monitoring method for foundation pits based on grey theory

prediction model is proposed in this research. Firstly， a grey theory prediction model and a first-order linear dynamic differential equation are established， and the response function is calculated using sample data and the time and state sequences of excavation deformation parameters. The function values are transformed into test point forms， and the vector and weight parameters of each point are solved as the initial reference for the model. Secondly， the initial sequence of the monitoring model is established， and the least squares integration method is used to generate the monitoring mean equation， then the background value， grayscale value， and proximity coefficient are calculated.Finally，the linear relationship is compared to provide the residual condition sequence of the monitoring points， and to obtain the implementable conditions of the monitoring model to effectively monitor the deformation of the foundation pit. The experimental verification was carried out using the Ocean New Light Commercial Complex project as an example， and the results showed that the grey theory prediction model has high monitoring accuracy， small errors， and strong practicality.

Key words

Grey theory prediction model;Foundation pit deformation;Response function;State sequence;Monitoring mean equation

（本文责编：冯 婷）