基于改进麻雀算法优化LSSVM的建筑沉降预测

摘 要：为了提高建筑沉降预测精度，本文提出了一种基于改进麻雀算法（Improved Sparrow Search Algorithm，ISSA）优化最小二乘支持向量机（Least Squares Support Vector Machine，LSSVM）的建筑沉降预测方法。利用圆混沌映射和莱维飞行策略对麻雀算法进行改进，提升了ISSA算法的寻优性能，采用ISSA算法确定LSSVM最优参数，构建基于ISSA-LSSVM的建筑沉降预测模型。算例分析结果表明，ISSA-LSSVM模型建筑沉降量预测结果的平均相对误差和均方根误差分别为3.114%和0.889mm，预测精度和误差波动性均优于其他方法，验证了本文所提建筑沉降预测方法的可行性与优越性。

关键词：建筑沉降；最小二乘支持向量机；改进麻雀算法

中图分类号：U 41 " 文献标志码：A

基坑开挖会对周围土体产生影响，破坏土层完整性，轻则造成地表开裂、建筑物倾斜，影响居民的正常生活，重则造成建筑物坍塌，构成安全事故[1-2]。为了防止安全事故发生，对基坑开挖后引起的建筑沉降预测进行研究是非常有必要的，建筑沉降精准预测能够对基础开挖的风险进行初步判断，并提前采取预控措施[3-4]。

为了对建筑沉降进行精准预测，专家们对此进行了大量研究。邵珠山等[5]将BP神经网络模型和GM（1，1）模型相结合，并深入挖掘建筑沉降样本数据之间的内部信息，提出了一种基于GM-BP的建筑沉降组合预测方法，通过算例仿真验证了该方法具有较高的预测精度。周渊[6]针对BP神经网络训练效果不佳的问题，采用非线性收敛因子和比例权重两种策略对灰狼算法进行改进，通过实际算例验证了该方法的有效性。现有建筑沉降预测方法虽然能够实现建筑沉降预测，但普遍存在预测结果稳定性较差和适应性不佳等问题，高精度建筑沉降预测方法有待进一步研究。

1 改进麻雀搜索算法

1.1 麻雀搜索算法

麻雀搜索算法（Sparrow Search Algorithm，SSA）是通过模仿麻雀种群觅食和反抓捕行为提出的一种寻优算法[7]。在麻雀种群中，将所有个体分为领导者、觅食者和警戒者。在麻雀种群觅食过程中，领导者采用公式（1）更新自身位置。

（1）

式中：j=1，2，…，d，其中，d为搜索空间的维度；h为当前进化次数；Xh+1 i，j为第i只麻雀在第j维空间上下一次进化后的位置；Xh i，j为第i只麻雀在第j维搜索空间的当前位置；θ为随机数，取值为[0，1]；hmax为最大进化次数；I为单位矩阵；ST为安全边界值；R2为警戒边界值；Q 为满足正态分布的随机数。

在公式（1）中，警戒边界值R2和安全边界值ST表示搜索区域是否安全，当前者大于后者时，表示搜索区域是安全的，该区域不存在天敌偷袭。反之，表示搜索区域不安全，该区域存在天敌，麻雀种群需要紧急撤离。

觅食者位置如公式（2）所示。

（2）

式中：B为个体总数；Xh worst 为当前最差位置；当满足条件时，表示觅食者位置不理想，无法找到食物；Xh+1 p "为下一次进化后的最优位置；A为行矩阵，矩阵中的元素为1或-1，且有A+=AT（A+AT）-1。

警戒者的位置如公式（3）所示。

（3）

式中：ς为步长修正系数；r为随机数，取值为（0，1）；Xh best为当前最好位置；fw为最佳位置适应度值；fi为第i只麻雀位置适应度值；fg为最差位置适应度值，当figt;fg时，表示麻雀位置离食物位置较远，当fi=fg时，表明麻雀位置很差，种群须及时更新位置。

1.2 SSA算法改进

SSA算法操作简单，容易实现，在2020年后广泛应用于各个领域。但当优化多维函数时，SSA算法容易向原点收敛，从而陷入局部最优。为了解决这个问题，本文采用下列策略对SSA算法进行改进，获得寻优精度更高的改进麻雀算法（Improved Sparrow Search Algorithm，SSA）。

1.2.1 圆混沌映射

原始麻雀种群在搜索空间中是随机产生的，这种方式容易造成个体分布不均匀，影响算法搜索性能。圆混沌映射是一种典型的混沌映射，可以产生分布均匀的随机序列，映射过程如公式（4）所示。

（4）

式中：zk+1为圆混沌映射位置序列；zk为初始位置序列；a、b为混沌映射系数。

1.2.2 莱维飞行

SSA算法在迭代后期易陷入局部最优，因此，本文在追随者位置更新公式中引入满足莱维飞行策略的自适应权重，以提高SSA算法跳出局部最优的能力。其飞行步长的数学模型如公式（5）所示。

（5）

式中：Levy（β）为服从的莱维飞行轨迹，β∈（0，2）； v、μ分别服从N（0，1）和N（0，σ2）分布，其中，采用公式（3）计算σ，计算过程如公式（6）所示。

（6）

式中：Γ（）为伽马函数。

每个麻雀个体位置Xi+1基于上一个个体位置进行莱维飞行后可得公式（7）。

Xi+1=Xi+φ∙Levy（β） " （7）

式中：Xi+1为莱维飞行变换后的位置；φ为步长调节系数；Xi为当前位置。

2 最小二乘支持向量机

1995年，研究人员在（Support Vector Machine，SVM）的基础上进行改进，并提出了最小二乘支持向量机（Least Squares Support Vector Machine，LSSVM）算法。与SVM的区别为LSSVM损失函数采用的是最小二乘线性系统，约束条件采用等式约束。通过上述改进，LSSVM将凸二次规划问题的求解转化为线性问题，不仅减少了计算量，也提升了计算精度[8]。

LSSVM进行回归拟合时的优化目标如公式（8）所示。

（8）

式中：ξi为误差；C为惩罚系数；w为权值；b为阈值；l为样本容量。

在公式（5）中引入拉格朗日函数，经过偏导计算，最终可以得到LSSVM回归函数，如公式（9）所示。

（9）

式中：K（x，xi）为径向基核函数。其计算过程如公式（10）所示。

（10）

式中：σ为核函数系数。

LSSVM的预测效果受其惩罚系数与核函数系数影响很大，因此为了提高LSSVM的性能，需要对二者进行优化。

3 构建ISSA-LSSVM建筑沉降预测模型

研究表明，建筑沉降主要受基坑开挖深度、土体重度、邻近建筑层数、支护结构插入比等因素的影响，且建筑沉降大小与各影响因素存在一定的非线性关系，因此本文以上述影响因素为支持向量，建筑沉降量为输出量，采用ISSA算法对惩罚系数与核函数系数进行优化，构建基于ISSA-LSSVM的建筑沉降预测模型，该模型的主要构建步骤如下。获取由4种影响因素和建筑沉降量组成的样本数据，并进行归一化处理。初始化LSSVM，设置ISSA算法相关参数，将LSSVM参数作为ISSA算法的寻优目标。利用圆混沌映射产生初始麻雀种群，利用公式（11）计算个体初始适应度值。

（11）

式中：N为样本容量；yi、yi*分别为建筑沉降量的实际值和预测值。执行迭代计算，分别更新领导者、觅食者和警戒者的位置。利用公式（11）重新计算麻雀个体适应度值并排序，更新当前最优解。判断迭代计算是否需要终止，当达到目标精度或迭代次数上限时，终止迭代，否则返回迭代计算。利用ISSA-LSSVM模型进行建筑沉降量预测。

4 算例分析

采用西南地区某建筑设计院的建筑沉降样本数据进行算例分析，样本数据共计58组，选取其中50组数据作为训练集，用于ISSA-LSSVM模型训练，将其余8组数据作为测试集，用于检验ISSA-LSSVM模型预测效果，测试集中的样本数据见表1。

改进麻雀算法参数设置[9]：麻雀总数为20，领导者、觅食者和警戒者占比依次为0.1、0.2和0.7，算法迭代次数上限值为200，混沌映射系数分别为0.3和1.3。

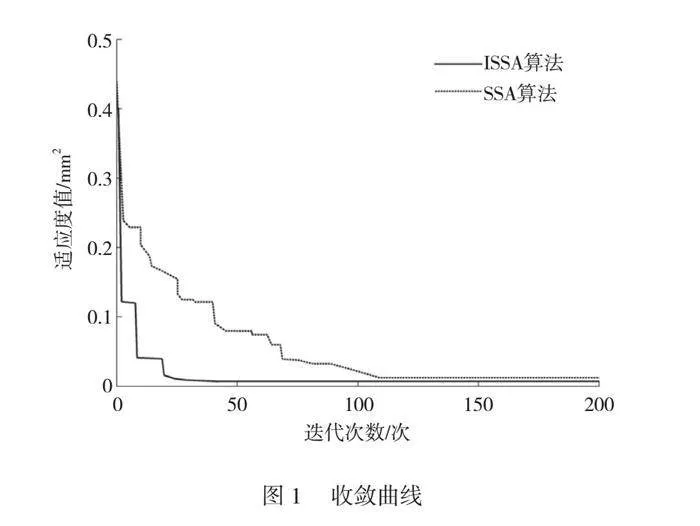
在Matlab2019b软件中编写计算程序，利用50组训练集样本进行训练，将基坑开挖深度、土体重度、邻近建筑层数、支护结构插入比作为输入量，将建筑沉降量作为输出量，分别利用ISSA算法和SSA算法对LSSVM进行参数优化，验证所提SSA算法改进策略的有效性。ISSA算法和SSA算法在优化过程中的收敛曲线如图1所示，可以看出，当适应度值趋于稳定时，ISSA算法比SSA算法迭代计算的次数更少，最终ISSA算法收敛时对应的适应度值更小，说明与SSA算法相比，ISSA算法的计算精度更高，验证了本文采用圆混沌映射和莱维飞行策略对麻雀算法改进的有效性。

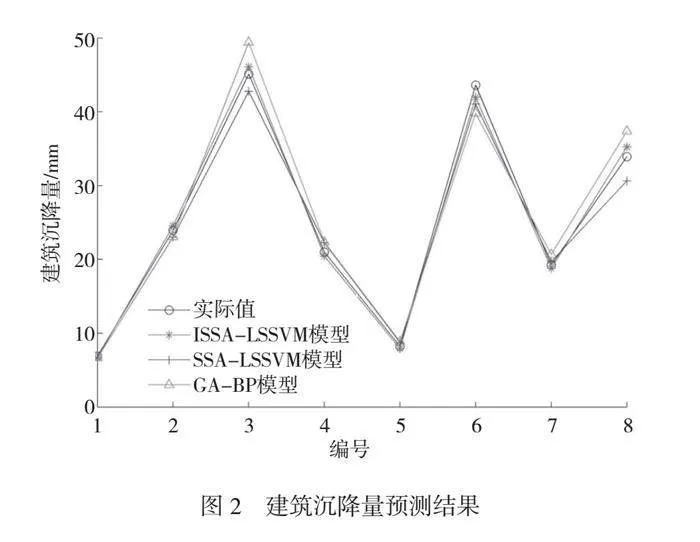
将ISSA算法和SSA算法的优化结果分别赋给LSSVM，建立ISSA-LSSVM模型和SSA-LSSVM模型，两种模型对测试集样本建筑沉降量预测结果如图2所示，为了对比分析，图2还给出了GA-BP模型的建筑沉降量预测结果。从建筑沉降量预测结果可以看出，ISSA-LSSVM模型的建筑沉降量预测结果比SSA-LSSVM模型和GA-BP模型更接近真实值。

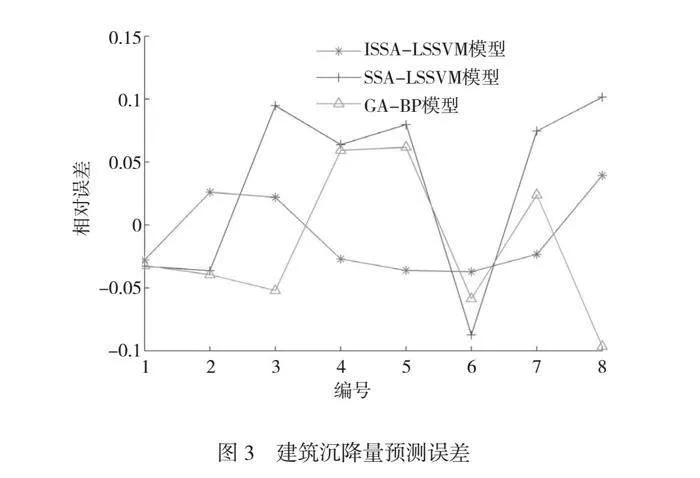
图3为ISSA-LSSVM模型、SSA-LSSVM模型和GA-BP模型建筑沉降量预测结果的相对误差，由图3可以看出，ISSA-LSSVM模型预测误差为[-0.0372，0.0393]，SSA-LSSVM模型预测误差为[-0.0965，0.0617]，GA-BP模型预测误差为[-0.0874，0.1015]，由此可见，ISSA-LSSVM模型建筑沉降量预测结果的误差波动更小。

为了进一步分析上述3种建筑沉降量预测模型的预测效果，采用公式（12）和公式（13）计算建筑沉降量预测结果的平均相对误差和均方根误差。

（12）

（13）

式中：εMAPE为平均相对误差；εRMSE为均方根误差。

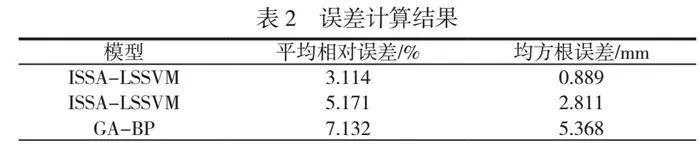
计算ISSA-LSSVM模型、SSA-LSSVM模型和GA-BP模型建筑沉降量预测结果的平均相对误差和均方根误差，见表2，由表2可知，ISSA-LSSVM模型建筑沉降量预测结果的平均相对误差和均方根误差分别为3.114%和0.889mm，两项误差均比SSA-LSSVM模型和GA-BP模型更小，可见ISSA-LSSVM模型不仅能够提高建筑沉降量预测精度，还能降低预测过程的波动性，验证了本文所提建筑沉降预测方法的可行性与优越性。

5 结论

本文以基坑开挖深度、土体重度、邻近建筑层数、支护结构插入比为支持向量，建筑沉降量为输出量，利用ISSA算法对LSSVM进行参数优化，构建了基于ISSA-LSSVM的建筑沉降预测模型。采用建筑沉降样本数据进行算例分析，并将ISSA-LSSVM模型的建筑沉降量预测结果与SSA-LSSVM模型和GA-BP模型进行对比，结果表明，ISSA-LSSVM模型不仅能提高建筑沉降量预测精度，还能降低预测过程的波动性。

参考文献

[1]滕雷，魏长寿，王俊杰，等. 基于动态Verhulst模型对高层建筑沉降预测的应用研究 [J]. 测绘技术装备， 2022， 24 （1）： 41-44.

[2]付伟，白洪伟，董杰，等. 灰色-小波神经网络在高层建筑物沉降预测中的应用 [J]. 皖西学院学报， 2022， 38 （5）： 105-109.

[3]张明智，张明栋. 基于灰色荷载预测的多元线性模型预测高层建筑沉降 [J]. 测绘与空间地理信息， 2024， 47 （5）： 195-197，201.

[4]王景环，汪亚民，郑松岗，等. 基于TCN与SVM组合模型的建筑沉降预测 [J]. 工程勘察， 2024， 52 （2）： 64-67，72.

[5]邵珠山，徐腾，张宇鹏. 改进GM-BP神经网络模型的高层建筑沉降预测 [J]. 建设科技， 2021（16）： 84-88.

[6]周渊. 基于I-GWO-BP模型的临近建筑沉降预测 [J]. 安徽建筑， 2024， 31 （4）：130-132.

[7]侯克鹏，包广拓，孙华芬. SSA-MLP模型在岩质边坡稳定性预测中的应用 [J]. 安全与环境学报， 2024， 24 （5）： 1795-1803.

[8]张志浩，熊文洁，钟文，等. 基于改进PSO-DE融合算法优化LSSVM的短期风功率预测 [J]. 山东电力技术， 2022， 49 （10）： 9-15.

[9]丁苗，陈琨，刘炬，等. 基于改进麻雀搜索算法的配电网分布式电源优化配置 [J]. 安徽电气工程职业技术学院学报， 2023， 28 （3）： 12-19.