电厂源-荷-储协调电力系统优化调度探究

摘 要：在电源、负荷、储能设备所构成的电力系统中，为了适应新能源占比不断提高的背景，研究过程将新能源发电形式设定为风力发电，建立了源-荷-储协调电力系统深度调峰优化调度模型。该模型引入2个控制目标，分别为系统总成本最低和弃风率最低，求解时需要满足一系列约束条件。在完成建模后，利用电力仿真软件建立1个有30个节点的电力系统模型，涵盖传统火电机组、风电场、储能设备以及负荷，用于验证优化调度模型的应用效果。根据研究内容得出以下结论：对比其他4种调度模式，本文建立的优化调度模型实现了总成本和弃风率最低的目标；提高风机装机容量会导致弃风率增加，总成本随之下降，因此需要结合实际情况选择合理的装机容量，以平衡弃风率和总成本之间的矛盾。

关键词：源-荷-储协调；电力系统深度调峰；优化调度模型

中图分类号：TM 73" 文献标志码：A

在国内的电力系统中，火力发电和风力发电均属于重要的电源形式，随着风电占比不断提高，对电力系统的调峰调度能力提出更高的要求，设计重点为保证电力调度的灵活性和总体的经济效益。为了满足以上发展需求，在此次研究中，创新性地提出源-荷-储协调电力系统深度调峰优化调度模型，实现了风电弃风率最低和系统总成本最低的控制目标，为优化调度模式、降低运营成本、提高电能质量创造了新的技术发展方向。

1 源-荷-储协调电力系统深度调峰优化调度方法

1.1 源-荷-储协调电力系统深度调峰优化调度模型

1.1.1 确定控制目标

源-荷-储协调要求电力系统的电源端、负荷端和储能设备端实现协调运行，其主要目的为提高电力系统的经济性。新能源的并网发电量持续增加，对电力系统的调峰能力提出了较高的要求。在电力系统深度调峰的背景下，如果将经济效益最高作为目标，那么主要的调峰对象为新能源发电，进而抑制新能源发电量[1]。如果将新能源发电消纳量最高作为目标，就会影响传统火力发电的经济性。因此，以上2种控制目标均存在一定的局限性。

在此次研究中，新能源发电形式为风电，针对源-荷-储协调电力系统深度调峰优化调度模型设置2个控制目标，分别为提高电网经济性和风电消纳量[2]。其中，风电消纳量可通过电网弃风率进行评价，弃风率越小，代表风电消纳量越高。

1.1.2 建立目标函数

优化调度模型具有2个目标参数，并且2个目标参数的量纲不同。当构建目标函数时，先通过标幺化处理消除量纲的影响，再利用线性权重变换为2个目标分配权重[3]。目标函数如公式（1）所示。

（1）

式中：F为目标函数；ω1为源-荷-储电力系统经济性权重系数；ω2为源-荷-储电力系统弃风率重系数；f1为源-荷-储电力系统运行成本；f2为源-荷-储电力系统弃风率；C0为经济性最优对应的模型优化结果；ρ0为弃风率最低对应的模型弃风率优化结果。

其中，权重系数ω1+ω2=1。

在目标函数中，参数f1、f2、C0如公式（2）所示。

（2）

式中：Cgi，t为火电机组调峰运行的费用；CW为弃风惩罚成本；CB为电力系统的备用成本；Ccha为储能设施的运行费用；Pf，t为风电的预测值；PW，t为风电的并网功率；Δt为风电并网发电的时长；C1为机组的煤成本；C2为风电设备的运行成本。

1.2 优化调度模型约束条件

1.2.1 火电功率约束

火电功率约束分为2种情况，其一为常规调峰时段的出力约束，其二为深度调峰时段的出力约束。在常规调峰阶段，约束条件为Pgi，min≤Pgi，t≤Pgi，max[4]。其中，将火电机组技术出力最小值记为Pgi，min，最大值记为Pgi，max，Pgi，t为火电机组在时间t时对应的实际出力。在深度调峰阶段，约束条件为Pgi，b≤

Pgi，t≤Pgi，max（Pgi，b为调峰机组的投油出力下限）。

1.2.2 风电功率约束

风电功率约束条件较简单，即风电的实际并网功率不超过风电预测值。因此，在模型计算阶段，必须确保预测值的误差控制效果。

1.2.3 线路传输容量约束

电力导线的传输容量具有一定的限制，当电流超过导线的传输容量时，可导致线路过热，严重时可引起线路损毁。针对线路传输容量的约束条件为-Pij，max≤Bij（θi，t-θj，t）≤Pij，max（Pij，max为线路节点i和j之间的传输容量最大值；Bij为i、j 2个线路节点之间的导纳；θi，t、θj，t分别为节点i、j在时间t时对应的电压相角[5]）。

1.2.4 需求响应约束条件

在同一个电力调度阶段，需求响应前后的电力负荷为恒定值。优化调度模型改变了用电方式，进而决定了用户的购电成本。因此，在深度调峰调度优化模型中，需要考虑用户满意度问题，将其作为必要的约束条件。用户满意度实际上分为2个维度，包括用电方式满意度和电费满意度。以电费满意度为例，其约束条件如公式（3）所示。

（3）

式中：PL1，t为原始负荷值；p1，t为对应的电价；PL2，t为计及需求响应之后的负荷值；p2，t为对应的电价；SP min为电费满意度上限；T为电力调度的总时长；t为电力调度期间的任意时间点。

1.2.5 火电主动性约束条件

在源-荷-储协调电力系统中，储能设施对调峰过程具有重要的影响。一方面，储能设施可增强调峰过程的灵活性，为电力系统获得调峰补偿创造有利的条件。另一方面，储能设施在充放电过程中会产生一定的附加成本。

在深度调峰阶段，将对应的火电利润记为Ug，t，风电利润记为UW，t。当UW，tlt;0并且Ug，tgt;0时，风电场不能通过参与深度调峰获得经济利益，因而会退出调峰；当UW，tgt;0，并且Ug，tlt;0时，火电厂不能通过参与深度调峰获得经济效益，因而退出调峰活动[6]。

1.3 优化调度模型求解流程

根据以上目标函数和约束条件，源-荷-储协调电力系统深度调峰优化调度模型的求解流程如下。1）将系统运行成本最低作为目标，利用负荷需求响应优化负荷曲线，判断是否满足负荷需求响应以及各种约束条件。2）当满足上一步的判断条件时，以系统运行成本最低为目标，允许系统中的火电机组进行深度调峰。根据优化后的负荷曲线安排火电机组的常规出力，同时进行深度调峰操作，判断是否满足相应的约束条件。3）将以上优化结果对应的运行成本和弃风率作为基准值，输入目标函数。按照弃风率和运行成本最低进行系统优化。4）根据优化后的负荷曲线安排机组出力、设备容量、储能设备的放电功率、调峰结果的利益分配，同时判断优化成果是否满足各类约束条件[7]。

2 基于优化调度模型的算例分析

2.1 算例模型及相关参数

2.1.1 算例模型选取

在算例分析阶段，采用图1所示的30节点电力系统。该模型中设置了1个风电场、6个火电机组以及若干储能设备，G1～G6为传统火电机组。黑色粗实线代表母线，黑色箭头代表负荷。

2.1.2 模型参数设置

2.1.2.1 火电机组参数设置

火电机组的参数包括出力上限、出力下限、燃料成本相关的系数以及机组爬坡率。在仿真模拟中，按照表1设置火电机组的参数，将机组燃煤成本记为C1，t，成本和燃料成本系数之间的关系如公式（4）所示。

C1，t=aiP2gi，t+biPgi，t+ci （4）

式中：ai、bi、ci为燃料成本系数。

2.1.2.2 储能设备参数设置

储能充电功率最大值设置为8MW，最小值设置为2MW；不考虑损耗，将储能设备的最大、最小放电功率分别设置为8MW、2MW；储能设备的初始荷电状态设置为6MW；储能设备的充、放电效率均按照95%进行取值；储能容量设置为20MW。

2.2 调度模式设置

在仿真过程中，设置5种互为对照的调度模式，各种模式的具体情况如下。1）模式1。以系统运行成本最低为目标，由火电机组参与常规调峰。2）模式2。以系统运行成本最低为目标，在考虑负荷需求响应的情况下，由火电机组参与常规调峰。3）模式3。以系统运行成本最低为目标，在考虑负荷需求响应的情况下，由G1机组参与深度调峰。4）模式4。以系统运行成本和弃风率最低为目标，在考虑负荷需求响应的情况下由G1机组参与深度调峰。5）模式5。以系统运行成本和弃风率最低为目标，配置储能设施，在考虑负荷需求响应的情况下，由G1机组参与深度调峰。

2.3 仿真数据分析

2.3.1 风机装机容量对优化调度的影响

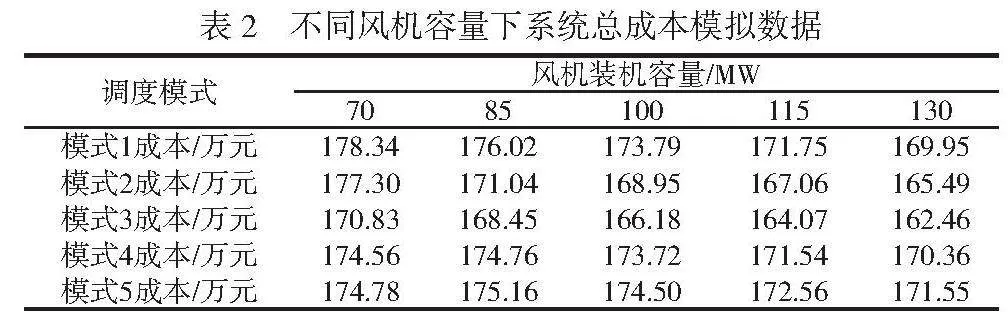
仿真过程将风机总装机容量分别设置为70MW、85MW、100MW、115MW、130MW。在以上5种调度模式下模拟装机容量对系统总成本和弃风率2个控制目标的影响，结果如下。

2.3.1.1 风机装机容量对系统总成本的影响

在5种调度模式下，不同风机装机容量对应的系统总成本模拟结果见表2。由仿真数据可知，在同一种调度模式下，随着风机容量增加，系统的总成本呈下降的趋势。当风机容量保持不变时，调度模式3的总成本最低，其次为调度模式2，其他3种调度模式差异较小。

表2 不同风机容量下系统总成本模拟数据

调度模式 风机装机容量/MW

70 85 100 115 130

模式1成本/万元 178.34 176.02 173.79 171.75 169.95

模式2成本/万元 177.30 171.04 168.95 167.06 165.49

模式3成本/万元 170.83 168.45 166.18 164.07 162.46

模式4成本/万元 174.56 174.76 173.72 171.54 170.36

模式5成本/万元 174.78 175.16 174.50 172.56 171.55

2.3.1.2 风机装机容量对弃风率的影响

在5种风机装机容量下，模拟5种调度模式对应的弃风率，结果如图2所示。

从图2中各个曲线的斜率变化趋势可知，随着风机装机容量提高，弃风率呈上升的趋势，弃风率的排序结果为模式5lt;模式4lt;模式3lt;模式2lt;模式1。

源-荷-储协调电力系统深度调峰优化调度模型（对应调度模式5）设计有2个控制目标，其一为系统总成本，其二为弃风率。从弃风率排序可知，此次建立的优化调度模型弃风率最低。

2.3.2 源-荷-储协调深度调峰优化调度模型综合效果

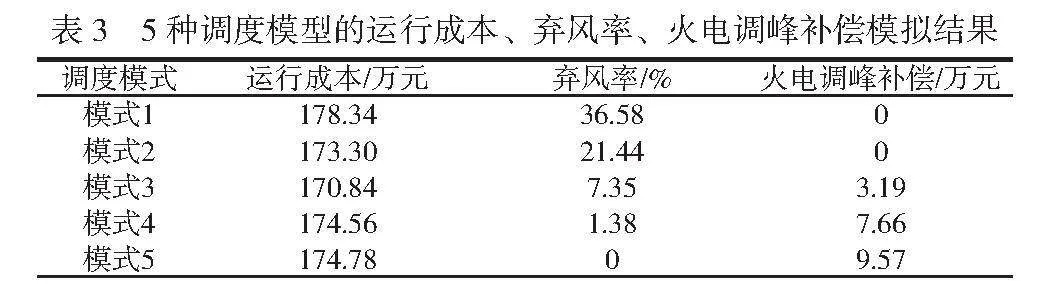
将目标函数中的ω1和ω2，均设置为0.5，以仿真模型为基础，利用5种调度模式开展电力系统调峰，模拟系统在调峰阶段的总成本、弃风率和火电调峰补偿。5种模型的风机总装机容量均为70MW，前4种调度模式不接入储能设备，第五种调度模式接入储能设备，调度模式5代表源-荷-储协调深度调峰优化调度模型。根据以上条件，仿真模拟结果见表3。

2.3.2.1 弃风率控制效果评价

优化调度模型的目标为总成本最低和弃风率最低。对比5种调度模式的弃风率，模式5最低，并且弃风率为0。显然，源-荷-储协调深度调峰优化调度模型的弃风率最低，明显优于其他调度模式。

2.3.2.2 系统总成本控制效果评价

系统总成本=运行成本-火电调峰补偿，按照该方法计算5种调度模式的总成本，模式1～模式5的总成本分别为178.34万元、173.30万元、167.65万元、166.90万元、165.21万元。可见，5种调度模式的总成本依次降低，模式5总成本最小。说明采用源-荷-储协调深度调峰优化调度模型能够有效降低深度调峰的总成本。综合弃风率指标，该模型达到了弃风率、总成本最低的目标。

表3 5种调度模型的运行成本、弃风率、火电调峰补偿模拟结果

调度模式 运行成本/万元 弃风率/% 火电调峰补偿/万元

模式1 178.34 36.58 0

模式2 173.30 21.44 0

模式3 170.84 7.35 3.19

模式4 174.56 1.38 7.66

模式5 174.78 0 9.57

3 结语

在新能源发电占比不断提高的背景下，为了强化电力系统的调峰能力，以适应新能源发电方式的特点。本文建立了源-荷-储协调电力系统深度调峰优化调度模型，主要实现火电、风电、储能设备和电力负荷的协调控制，得出以下基本结论。1）源-荷-储协调电力系统深度调峰优化调度模型的目标函数提出2个控制目标，其一为系统总成本最低，其二为风电弃风率最低。2）在2.3.1小节的仿真中，设置5种风机装机容量，对比不同调度模式下的弃风率和系统总成本。根据模拟数据可知，在提高风机装机容量的情况下，弃风率呈上升的趋势，总成本则不断下降。因此，2个控制目标存在矛盾，需要根据实际情况合理设计风机装机容量，实现2个目标的最优解。3）在2.3.2小节的仿真中，对比5种调度模式的弃风率和总成本，源-荷-储协调电力系统深度调峰优化调度模型（模式5）的弃风率和总成本均最低，达到了预期目标。

参考文献

[1]宋彦斌，汪莞乔，张慧，等.分布式“源荷储”资源协同互动异构组网方法与仿真实现[J].电子技术应用，2024，50（3）：73-79.

[2]曾梦迪，胡康涛，朱欣悦，等.新型混合储能运行模式分析与源荷储协调控制[J].电力电子技术，2024，58（2）：79-83.

[3]何玉灵，解奎，孙凯，等.基于改进布谷鸟算法的微电网源-荷-储功率优化调度[J].电力科学与工程，2023，39（10）：14-25.

[4]杨延栋，舒斐，马金晨，等.基于特征融合的配电网源-荷-储完全分布式协调控制方法[J].电气自动化，2023，45（4）：30-32，36.

[5]杨锡勇，张仰飞，林纲，等.考虑需求响应的源-荷-储多时间尺度协同优化调度策略[J].发电技术，2023，44（2）：253-260.

[6]郇政林，刘杰，徐沈智，等.面向高比例新能源接入的源-荷-储灵活性资源协调规划[J].电网与清洁能源，2022，38（7）：107-117.

[7]杨洪明，尹邦哲，孟科，等.考虑源荷功率矩不确定性的新型互联电力系统省内-省间分布鲁棒协调优化调度[J].电力建设，2023，44（7）：98-110.