基于插值修正的上证50ETF期权隐含高阶矩研究

摘要：期权隐含高阶矩是衡量金融资产波动性和非对称性的关键指标。然而，真实市场中期权的执行价格具有离散性和有界性，直接应用理论方法基于市场离散期权数据计算的隐含高阶矩存在近似误差，影响指标可靠性。本文利用上证50ETF期权数据，采用无模型方法计算隐含波动率和隐含偏度指标，并通过“内插-外推”方法进行修正。研究结果表明：①未修正的隐含高阶矩通常被高估；②隐含波动率指数与上证50ETF收益之间存在显著的负相关性，这支持了市场存在杠杆效应和波动率反馈效应的理论；③隐含偏度指数与上证50ETF收益之间存在显著的正相关性，这可以理解为投资者更偏好右偏资产，而右偏资产价值倾向于被高估，从而导致负的收益；④在大多数时期，已实现波动率比隐含波动率低，这表明大多数投资者大部分时间倾向于规避风险，并且愿意为对冲风险支付费用。

关键词：期权隐含高阶矩；上证50ETF；已实现高阶矩；风险溢价

一、引言

长期以来，期权价格中蕴含的信息一直是学术界和业界关注的焦点。早期研究表明，通过Black-Scholes（BS）公式可以获得隐含波动率（Black和Scholes，1973）。随着期权定价模型与技术手段的不断发展，研究者发现期权面板数据中还包含了更为复杂的信息，如隐含偏度。这些期权隐含信息被广泛认为是对真实测度下历史信息的重要补充，因为期权价格反映了标的资产在风险中性测度下的预期走势。本文主要探讨期权的隐含信息，包括隐含波动率和隐含偏度。这两者分别代表了风险中性测度下标的资产收益率的预期波动性和偏度。

提取期权价格中的隐含信息对学术界和业界都具有重要意义。在实际应用中，隐含信息可作为市场信号使用。例如，芝加哥期权交易所（CBOE）的市场波动率指数（VIX），通常被称为“恐慌指数”，用于预测未来市场波动率；中国波动率指数（iVIX）用于预警市场潜在风险，并作为投资者调整仓位的重要信号。隐含偏度可以反映股票的预期未来走势，隐含偏度值越小预示着未来资产收益分布越左偏，即资产收益出现下跌的概率会增加。除此之外，这些信息可以与真实测度下的信息结合，用于构建风险溢价指标，以反映市场预期和实际情况的偏差，从而为研究市场收益提供支持。因此，充分利用期权价格中的隐含信息可以为风险管理和金融资产定价提供有效指导。

一些重要文献研究了期权隐含高阶矩。例如，Christoffersen等（2013）总结了期权隐含信息的相关研究，介绍了两种构建期权隐含高阶矩的方法：参数方法（Heston，1993；Christoffersen等，2009）和无模型方法（Carr和Madan，1998）。相比之下，无模型方法无须依赖特定的模型设定，因此被认为更具灵活性。在实际市场中，芝加哥期权交易所就是采用无模型方法来计算VIX指数。

目前，关于期权隐含信息的研究已经取得了诸多成果。Jiang和Tian（2005）发现，无模型方法计算的隐含波动率可以更有效地预测未来实际波动率。郑振龙等（2016）利用S&P500指数期权的方差和偏度对股票横截面序列进行了回归分析。丛明舒（2018）发现，中国市场和美国市场的期权隐含信息对股票收益率的影响存在显著差异。

尽管无模型方法具有多种优势，但仍存在一些局限性，如它依赖期权执行价格连续性的假设。然而，在实际市场中，我们只能观察到离散的期权执行价格，因此这一假设并不成立。此外，期权执行价格的范围是有界的，这与计算公式中的无界假设不符。为了尽可能解决这些局限性，本文在无模型方法的基础上引入了“内插-外推”方法，以修正隐含高阶矩的估算值，并将修正后的隐含高阶矩信息应用于中国市场，进一步研究修正后的隐含高阶矩对50ETF收益率的影响，以及隐含高阶矩与已实现高阶矩之间的关系。此外，本文基于风险中性测度和真实测度构建了方差风险溢价指标，并研究了该指标对50ETF收益率的影响。

本文剩余的结构安排如下：第二部分详细介绍了隐含高阶矩指标的构建方法。第三部分分析了计算隐含高阶矩时近似误差的来源。第四部分提出了近似误差的修正方法。第五部分进行实证分析。第六部分总结本文的研究结论，并讨论其在实践中的潜在应用和意义。

二、隐含高阶矩构建

从期权面板数据中计算隐含高阶矩的方法主要分为有模型和无模型两种。由于前者容易受模型不确定性的影响，故本文主要借鉴Bakshi等（2003）关于无模型方法的思想来推导期权隐含高阶矩。设定R（t，τ）=lnS（t+τ）-lnS（t）为t时刻τ期的收益率，S（t）为t时刻资产的价格，则在t时刻τ期的风险中性收益率的隐含波动率和隐含偏度可以分别定义为：

Vol（t，τ）={Et［R（t，τ）-Et（R（t，τ））］2}1/2（1）

Skew（t，τ）=Et［R（t，τ）-Et（R（t，τ））］3{Et［R（t，τ）-Et（R（t，τ））］2}3/2（2）

这里，Et（·）为风险中性下的条件期望，即Et（·）=E（·|S（t））。

根据CBOE白皮书、Bakshi等（2003）以及Bali和Murray（2013）的研究，可以通过虚值期权数据推导出对应资产的隐含高阶矩：

Vol（t，τ）=（erτV（t，τ）-μ（t，τ）2）1/2（3）

Skew（t，τ）=erτW（t，τ）-3μ（t，τ）erτV（t，τ）+2μ（t，τ）3［erτV（t，τ）-μ（t，τ）2］3/2（4）

其中，μ（t，τ）=erτ-1-erτ2V（t，τ）-erτ6W（t，τ）-erτ24X（t，τ），r为无风险利率，τ为期权到期期限。隐含高阶矩中对应的函数V、W和X的具体形式如下：

V（t，τ）=∫∞S（t）21-lnKS（t）K2C（t，τ;K）dK+∫S（t）021+lnS（t）KK2P（t，τ;K）dK（5）

W（t，τ）=∫∞S（t）6lnKS（t）-3lnKS（t）2K2C（t，τ;K）dK-∫S（t）06lnS（t）K+3lnS（t）K2K2P（t，τ;K）dK（6）

X（t，τ）=∫∞S（t）12lnKS（t）2+4lnKS（t）3K2

C（t，τ;K）dK+∫S（t）012lnS（t）K2+4lnS（t）K3K2P（t，τ;K）dK（7）

其中，C（t，τ;K）和P（t，τ;K）分别是t时刻开始t+τ时刻到期且执行价格为K的看涨和看跌期权价格。

为了计算V、W和X，需要使用连续执行价格下的看涨和看跌期权的价格。然而，由于期权面板数据是离散的，只能利用离散的期权数据计算V、W和X。

V︿（t，τ）=∑nci=121-lnKciS（t）*Kci2C（t，τ;Kci）△Kci+∑npi=121+lnS（t）*KpiKpi2P（t，τ;Kpi）△Kpi（8）

W︿（t，τ）=∑nci=16lnKciS（t）*-3lnKciS（t）*2Kci2C（t，τ;Kci）△Kci-∑npi=16lnS（t）*Kpi+3lnS（t）*Kpi2Kpi2P（t，τ;Kpi）△Kpi（9）

X︿（t，τ）=∑nci=112lnKciS（t）*2+4lnKciS（t）*3Kci2C（t，τ;Kci）△Kci+∑npi=112lnS（t）*Kpi2+4lnS（t）*Kpi3Kpi2P（t，τ;Kpi）△Kpi（10）

这里，S（t）*=S（t）-PVDivs为除息后的股价，PVDivs为股息现值，Kci和Kpi分别为第i个虚值看涨期权和看跌期权的行权价，C（t，τ;Kci）和P（t，τ;Kpi）分别为第i个看涨和看跌期权的价格，nc和np分别为看涨和看跌期权的数量，对于2≤i≤nc，△Kci=Kci-1-Kci，△Kc1=S*t-Kc1，对于2≤i≤np，△Kpi=Kpi-1-Kpi，△Kp1=S*t-Kp1。这样通过离散方法可以计算出隐含波动率和隐含偏度。

为了估计无模型隐含高阶矩，式（8）～式（10）中给出的离散近似V︿、W︿和X︿会产生多种近似误差，如截断误差和离散化误差。这些误差可能对估计隐含高阶矩产生重要影响。接下来，将详细介绍每种近似误差。

三、近似误差来源

在本节中，笔者将探讨在利用离散期权数据计算隐含高阶矩时产生的两种近似误差，即截断误差和离散化误差。

（一）截断误差

截断误差是由于执行价格K范围有界导致的。正如V、W和X的定义所示，无模型隐含高阶矩的计算需要0到无穷的执行价格，然而，当使用离散化的数据进行计算时，只能利用有限范围的执行价格数据。记KL和KU分别是给定期限的最低和最高执行价格。由于无限范围的执行价格被有限范围的执行价格［KL，KU］所取代，因此可以得到以下近似式（先不考虑给定范围内的离散情况）：

V（t，τ）≈∫KUS（t）21-lnKS（t）K2C（t，τ;K）dK+∫S（t）KL21+lnS（t）KK2P（t，τ;K）dK（11）

W（t，τ）≈∫KUS（t）6lnKS（t）-3lnKS（t）2K2C（t，τ;K）dK-∫S（t）KL6lnS（t）K+3lnS（t）K2K2P（t，τ;K）dK（12）

X（t，τ）≈∫KUS（t）12lnKS（t）2+4lnKS（t）3K2C（t，τ;K）dK+∫S（t）KL12lnS（t）K2+4lnS（t）K3K2

P（t，τ;K）dK（13）

因此，V、W和X的截断误差由以下表达式给出：

Vtrunc=-∫∞KU21-lnKS（t）K2C（t，τ;K）dK+∫KL021+lnS（t）KK2P（t，τ;K）dK（14）

Wtrunc=-∫∞KU6lnKS（t）-3lnKS（t）2K2C（t，τ;K）dK-∫KL06lnS（t）K+3lnS（t）K2K2

P（t，τ;K）dK（15）

Xtrunc=-∫∞KU12lnKS（t）2+4lnKS（t）3K2

C（t，τ;K）dK+∫KL012lnS（t）K（t）2+4lnS（t）K3K2

P（t，τ;K）dK（16）

负号表明截断误差会导致计算的高阶矩产生负的偏差。

（二）离散化误差

离散化误差是由于数值积分导致的，因为CBOE在计算中采用式（8）、式（9）、式（10）。尽管从理论上看，数值积分误差可以通过使用足够精细的执行价格网络来最小化，但实际期权面板数据中可获取的离散数据始终是有限的，且行权价之间的离散程度往往很大，因此会产生较为明显的离散化误差。离散化误差可以表示为：

Vdisc=V︿（t，τ）-∫KUS（t）21-lnKS（t）K2C（t，τ;K）dK+∫S（t）KL21+lnS（t）KK2P（t，τ;K）dK（17）

Wdisc=W︿（t，τ）-∫KUS（t）6lnKS（t）-3lnKS（t）2K2C（t，τ;K）dK-∫S（t）KL6lnS（t）K+3lnS（t）K2K2

P（t，τ;K）dK（18）

Xdisc=X︿（t，τ）-∫KUS（t）12lnKS（t）2+4lnKS（t）3K2C（t，τ;K）dK+∫S（t）KL12lnS（t）K2+4lnS（t）K3K2

P（t，τ;K）dK（19）

四、近似误差的处理

近似误差主要由于期权数据在不同执行价格下的稀疏性引起。为了减少这种误差，需要获取更多执行价格对应的期权价格数据。解决这一问题的一种方法是通过“平滑”技术填补稀疏的期权数据。通常而言，“平滑”技术应用于期权合约的波动率，而非直接应用于期权价格。具体步骤如下：首先，利用BS公式计算已有期权价格对应的波动率；其次，使用“平滑”技术构建期权合约对应的波动率曲线，以获取所需执行价格对应的波动率；最后，再次利用BS公式计算相应执行价格的看涨和看跌期权价格。本文采用了一种有效的平滑方法来提取无模型波动率，即采用“内插-外推”方法构建波动率曲面。

（一）已有执行价格间的内插法

假定对于给定的到期日T有N个执行价格，分别为Ki，i=1，2，…，N，其对应的看涨看跌期权的市场价格分别是CM（Ki，T）和PM（Ki，T）。不失一般性，有0<KL=K1<K2<…<KN=KU<∞。这里仅使用OTM期权来建立波动率函数。通过BS模型，结合N个执行价格以及对应的期权价格，可以反推出这N个执行价格对应的波动率（σ（Ki，T），i=1，2，…，N）。

构建执行价格区间［KL，KU］上的波动率函数是关键。已有研究中，参数法和非参数法都被广泛应用（Bahra，2007；Bliss和Panigirtzoglou，2002；Anagnou等，2002）。然而，参数方法对模型形式的限制，无法灵活适应观测数据。因此，本文采用非参数方法来构建波动率函数，以便更好地处理和利用不同执行价格下的期权价格数据。

采用“内插法”在N个执行价格之间建立光滑函数，可以很好地拟合这N个已知的波动率。笔者希望在执行价格区间［KL，KU］找到一个可微函数f（K），有

f（Ki）=σ（Ki，T），i=1，2，…，N（20）

这里参考Jiang和Tian（2005），使用三次样条来拟合已知的波动率。为了使拟合结果更好，从K2到KN-1所有的内部执行价格均被用作节点来拟合三次样条。接着，对于新的内插点便可以通过f（K）获得其对应合约的波动率。

（二）已有执行价格外的外推法

由于在已列出的执行价格区间之外，没有已知的期权价格，而范围更广的执行价格对于计算隐含高阶矩有较大的好处，因此需要根据已构建的波动率函数对区间外的波动率进行外推。具体来说，考虑两种外推方法。

1平推法

平推法是指对于执行价格区间外的波动率，用最接近的已知波动率值来代替，即对于区间（0，KL］的波动率都用σ（KL）来代替，对于区间［KU，∞）的波动率都用σ（KU）来代替，其核心思想如图1上图所示，该方法常被用于波动率估计的修正。然而，“平推法”存在两个缺点：一是为了满足无套利条件，波动率函数需要保持连续性，但是“平推法”可能导致波动率函数在KL和KU处出现拐点，从而使风险中性概率密度函数变为负数；二是根据波动率“微笑”或者波动率“偏斜”的观察，随着执行价格远离当前股价，波动率往往会上升。因此，对于执行价格区间外的波动率使用常数波动率代替，可能会导致波动率被低估。

2线性外推法

线性外推法指的是在最低KL和最高KU的执行价格点上施加平滑条件，并保持一个线性的外推结构。具体来说，通过调整处于执行价格两边的线性外推斜率，使其与最低KL或最高KU执行价格内部端的斜率一致，如图1下图所示。这种方法确保了在整个执行价格范围内都有平滑的波动率曲线，并且能够很好地拟合已知的波动率数据。“线性外推法”构建的波动率曲线更符合通常观察到的波动率“微笑”或者波动率“偏斜”。

由此可见，一旦构建好波动率函数，适当范围内任意执行价格处的期权价格都可以通过使用BS模型根据相应拟合的波动率计算得到。这样一来，可以利用更多的期权数据对数值积分V、W和X进行离散化计算。

五、实证分析

（一）数据描述

本文选取2021年1月4日至2021年12月31日每天9：30到11：30以及13：00到15：00的50ETF指数和50ETF期权的1分钟级数据，共计243天（交易日），每天包含241个1分钟数据。剔除所有不满足无套利条件的期权样本，选择期权到期期限为10～60天，并且每天至少存在两支认购和认沽期权的样本。当数据处理完后，可以使用前面章节的方法计算出风险中性高阶矩，这里所计算的均为期限τ为30天的风险中性矩。

（二）修正方案间的比较分析

采用CBOE的指标构建方法，分别构建波动率指数和偏度指数：

iVIXt，τ=100*Volt，τ（21）

iSKEWt，τ=100-10*Skewt，τ（22）

本节对比分析了不同的“内插-外推”方法对50ETF波动率指数（iVIX）和偏度指数（iSKEW）的影响。鉴于截断误差和离散化误差，对不同方法进行比较分析，以评估其对iVIX和iSKEW的影响。对“内插-外推”方法进行两种不同的内插点数选择，分别为在已有执行价格区间内选择100个和500个等间距内插点。在内插计算完成后，还采用了线性外推和平值外推两种方法。对于线性外推，当内插点数为100时，考虑2个、10个和20个等间距外推点；当内插点数为500时，则考虑10个、50个和100个等间距外推点，以确保外推的区间长度一致。对于平值外推，外推点个数的选择与线性外推方法一致。

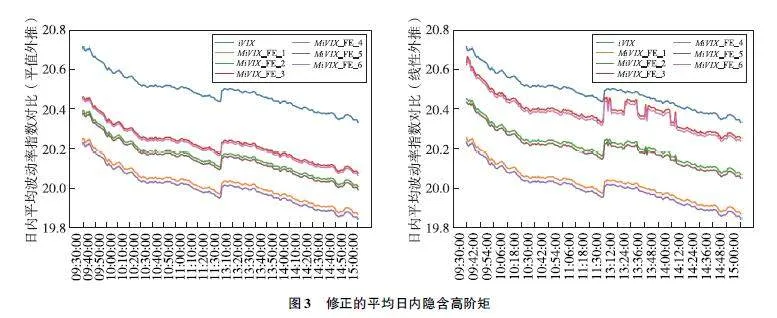
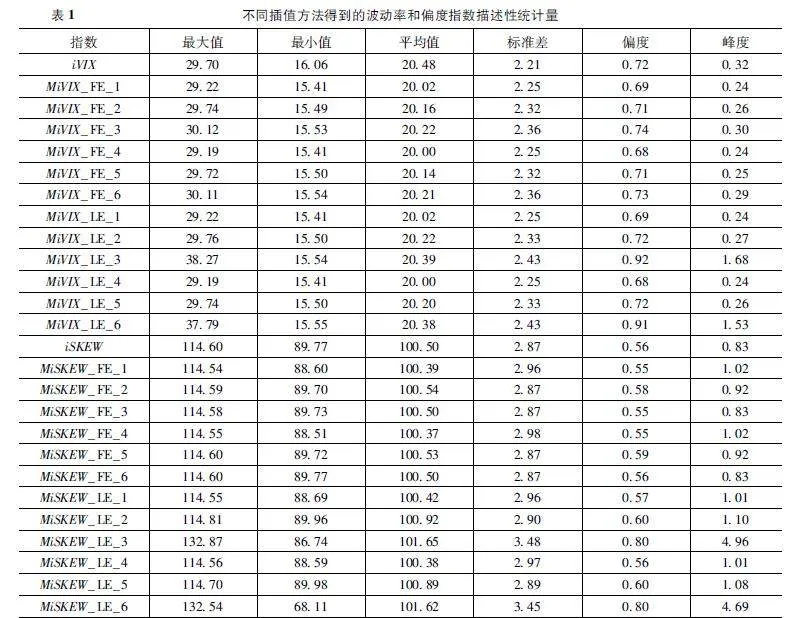
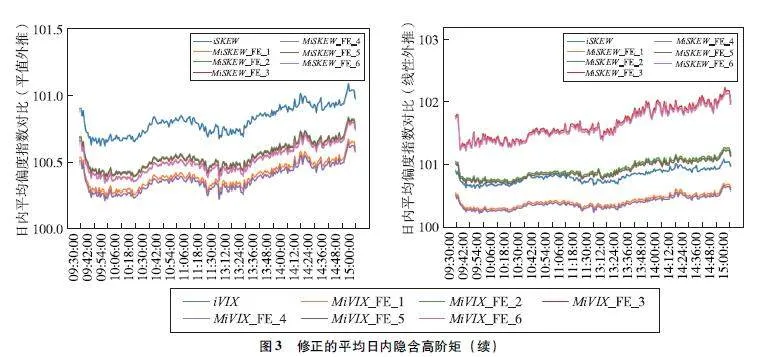
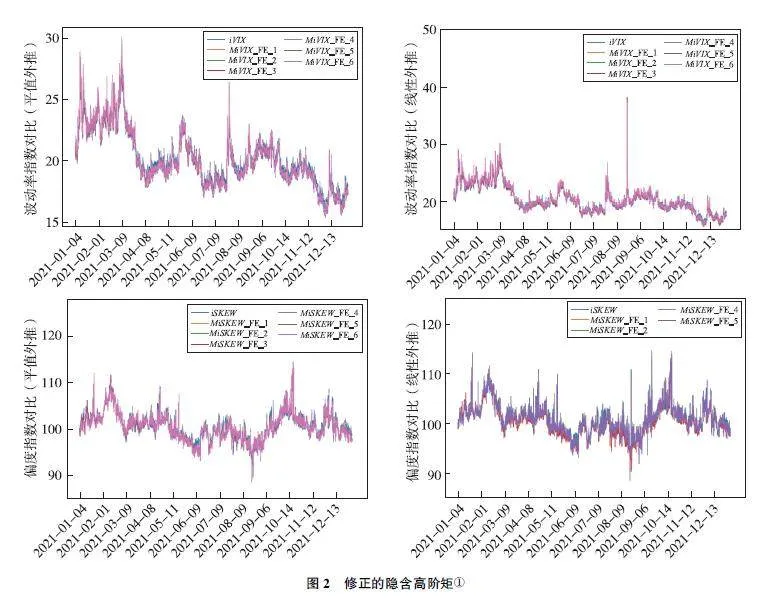
表1展示了不同插值方法计算的波动率指数和偏度指数的描述性统计。笔者观察到修正后的iVIX指数相对于未修正的iVIX指数，在均值和最小值上几乎都显示出下降趋势。具体而言，平值外推方法得到的iVIX指数相对于线性外推方法更小，且内插点数为500时的iVIX指数比内插点数为100时的iVIX指数要小。对于iSKEW的计算，平值外推对其影响不大。然而，当线性外推点数过多时会导致iSKEW值显著增加。

图2呈现了不同插值方法修正后的iVIX和iSKEW指数的时间序列。可以发现，未插值情况下的波动率和偏度指数一般位于所有插值计算结果之上，显示出插值后的指数普遍偏低。此外，线性外推点数过多可能会产生异常值。为了更好地显示不同方法之间的差异，图3展示了不同插值方法修正后的iVIX和iSKEW指数的平均日内走势。可以发现，对于平均日内iVIX指数，经过平值外推和线性外推修正后的波动率指数均低于未插值计算结果，且内插点数对其影响较小，而外推点数对其影响较大。对于平均日内iSKEW指数，平值外推修正的iSKEW指数低于未插值的计算结果。然而，线性外推修正的iSKEW指数在外推点数过多时会显著高于未插值的计算结果。因此，不建议使用过多的线性外推点数。

综上所述，未插值的隐含高阶矩往往存在高估的情况，这可能导致市场投资者在期权交易、金融资产定价、资产收益分析以及金融风险传染度量等方面做出错误的决策。并且内插点数越多，适度的线性外推结果越稳健。由于理论上采用插值计算的隐含高阶矩更为准确，且实证结果显示插值和不插值结果差异比较大。基于这些考量，选择了内插点数为500、外推点数为50的方案进行后续数据分析和实证研究。

（三）变量的描述性统计

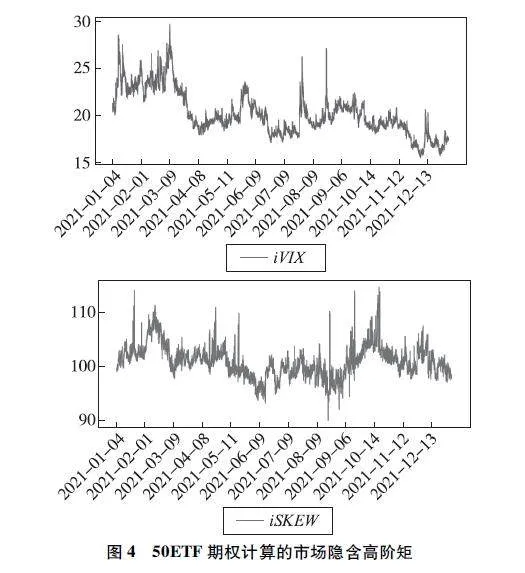
图4分别展示了修正后的iVIX指数和iSKEW指数的时间序列。以下是对图4结果的分析：①从iSKEW指数图中可以观察到，2021年中国市场的iSKEW指数有部分数值小于100，处于90～100，显示出市场预期收益率出现右偏的现象。这与Chang等（2013）在美国市场计算的隐含偏度指数始终

大于100有所不同。②iSKEW指数通常在达到115之后会下跌，而不是持续上升，这是因为市场上存在套利机会的投资者，他们的介入会使iSKEW指数回归其均值附近，从而避免持续的左偏现象。这些分析结果揭示了市场波动率和偏度指数在不同时间段的动态变化，对理解市场行为和制定投资策略具有重要意义。

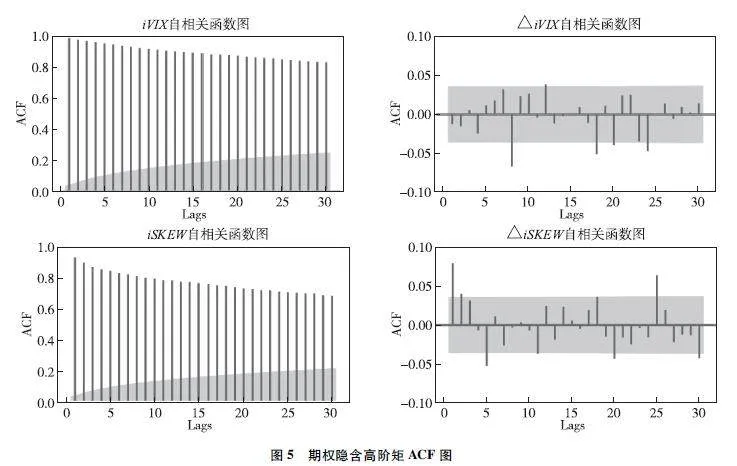
图5显示了以下内容：左侧为iVIX指数和iSKEW指数本身的自相关图；右侧则展示了对iVIX指数和iSKEW指数进行差分后的自相关图。在自相关图中，阴影部分表示95%的置信区间。观察图可知，iVIX指数和iSKEW指数本身具有显著的自相关性，然而，经过一阶差分处理后，大部分iVIX指数和iSKEW指数的自相关系数均落在95%的置信区间内。这表明对隐含高阶矩进行差分处理后的时间序列更加平稳。

（四）回归分析

1收益率回归分析

Jondeau等（2019）在其研究中使用美国数据发现，偏度可以影响个股的收益率。Harvey和Siddique（2000，2000）的研究结果显示，偏度不仅影响个股的收益率，还对整个股票市场的收益率产生影响。那么，在中国市场，隐含高阶矩是否会对50ETF的收益率产生影响呢？

为了研究隐含高阶矩对上证50ETF指数收益的影响，本节使用了差分后的iVIX指数、iSKEW指数及其组合对上证50ETF指数的收益率进行回归分析。研究数据覆盖了2021年1月4日至2021年12月31日的243个交易日的50ETF和期权数据。我们建立了以下三个模型：

Model1：Rt=α+β1△iVIXt+t（23）

Model2：Rt=α+β2△iSKEWt+t（24）

Model3：Rt=α+β1△iVIXt+β2△iSKEWt+t（25）

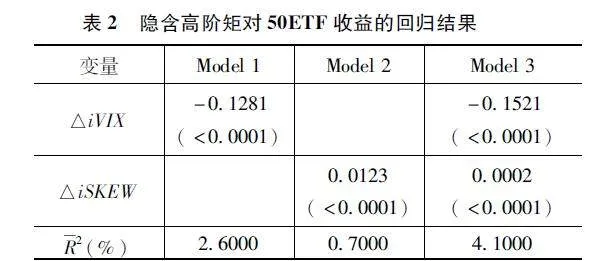
这里的Rt是第t个时刻50ETF的对数价格收益率，△iVIXt=iVIXt-iVIXt-1，△iSKEWt=iSKEWt-iSKEWt-1。表2展示了隐含高阶矩与市场收益率回归的结果。

从表2的回归结果可以得出：①收益率与△iVIX之间表现出显著的负相关性，这种关系主要是由于杠杆效应和波动率反馈效应所导致的。②△iSKEW对收益率具有显著的预测能力，这可以理解为投资者更偏好右偏的资产，而右偏的资产往往被高估，从而导致负的收益。此外，当iSKEW>100时，表明资产收益存在左偏的可能性，进一步指示资产收益下跌的风险增加。由于风险厌恶的投资者会寻求更多的风险补偿来规避尾部风险的影响，因此更高的△iSKEW通常伴随着更高的资产收益。③当△iVIX和△iSKEW同时加入收益率的回归模型后，它们对收益率的影响依然显著。这表明，从期权数据中提取的隐含高阶矩均包含了影响50ETF收益率的重要信息。

2已实现高阶矩之间的回归分析

通过期权数据计算的隐含波动率指数和隐含偏度指数间接反映了投资者对市场风险的度量，而已实现波动率（RV）和已实现偏度（RSkew）是直接通过50ETF收益率数据计算的，能够直接反映资产的收益情况，因此它们之间存在一定的关联。在本节中，建立已实现高阶矩与隐含高阶矩之间的回归模型，并分析它们之间的关系。首先，根据Andersen和Bollerslev（1998）及后续文献提出的方法，构建已实现高阶矩：

RVt=∑N～i=0R2t-i（26）

RSkewt=N～∑N～i=1R3t-i（RVt）3/2（27）

RSKEWt=100-10×RSkewt（28）

这里，Rt-i表示第t-i时刻的对数收益率。使用滑动步长为1分钟，窗宽大小N～为240分钟的数据集来计算高频RV和RSkewt。接下来，建立已实现高阶矩与隐含高阶矩之间的回归关系模型：

RV2t=α+βiVIX2t+t（29）

RSKEWt=α+βiSKEWt+t（30）

使用修正后的隐含波动率指数和隐含偏度指数，得到的回归结果如下：

RV2t=-00294+15606iVIX2t（-969840）（2187779）（31）

RSKEWt=1570276-05636iSKEWt

（595898）（-215865）（32）

其中括号内为各个系数的t-统计量。从隐含高阶矩对已实现高阶矩的回归结果可以看出：①已实现波动率和iVIX指数之间存在显著的正相关关系；②已实现偏度指数与iSKEW指数之间存在显著的负相关关系。由此可以说明50ETF期权隐含信息对50ETF收益率的方差和偏度具有一定的解释作用。

3方差风险溢价回归分析

已实现波动率反映了投资者对市场真实风险的度量，而隐含波动率则反映了对未来波动率风险的预期。因此，方差风险溢价（VRP）可以定义为在风险中性测度下的方差减去真实测度下的已实现方差，即VRPt=iVIX2t-RV2t。VRP在一定程度上反映了投资者的风险规避程度。图6展示了高频已实现波动率（RV）和隐含波动率（iVIX）的时间序列，可以观察到在许多时段，iVIX比RV要大。

图7呈现了方差风险溢价。可以看出，VRP大多时候都是大于0的，这说明中国投资者更倾向于规避风险。当未来市场走向不确定增加时，投资者规避风险的意愿会增强，导致VRP处于一个较高的水平。然而，当市场出现高波动（如2021年2月以及2021年7月）时，VRP会出现很大的负值。这表明在这些时期，市场相对较为动荡，导致真实市场中由50ETF价格直接计算的已实现波动率要高于投资者的预期波动率。

Bollerslev等（2009）使用美国数据发现VRP在对季度收益率的预测上表现最为强烈；Qiao等（2024）则利用9个新兴市场的指数构建VRP，发现VRP可以预测股指收益、货币收益以及资本流动，并且在短期内预测效果尤其显著。本节利用插值的隐含波动率指数计算VRP，并研究其对上证50ETF收益率的影响。建立以下回归模型：

Rt=α+βVRPt+t（33）

其中，Rt表示第t个时刻50ETF的对数价格收益率，VRPt表示第t个时刻的方差风险溢价。得到的回归结果如下：

Rt=-00744+57866VRPt

（-03819）（05615）（34）

括号内为参数估计的t-统计量。回归结果显示，截距项和斜率项在95%置信水平下均不显著，表明VRP对上证50ETF的收益率没有显著的影响，这与田凤平和杨科（2021）的研究结果一致。

六、结论

本文利用上证50ETF及其期权数据，采用“内插-外推”方法，计算了50ETF指数的风险中性隐含高阶矩，并将其与基于CBOE白皮书未插值计算的隐含高阶矩进行了比较。结果显示，未插值处理的隐含波动率指数和隐含偏度指数都存在一定程度的被高估。隐含波动率的被高估通常意味着期权价格可能也被高估，这可能误导依赖隐含波动率指数进行期权交易的投资者，从而导致损失。鉴于国内期权市场近年来的快速发展，精确构建隐含波动率和偏度指标对维护投资者信心和衍生品市场的稳定发展至关重要。因此，本文建议采用基于“内插-外推”方法修正的隐含波动率和隐含偏度作为新的研究指标。

同时，本文还研究了插值后的隐含高阶矩信息对50ETF收益率以及已实现高阶矩的影响，并进一步基于隐含高阶矩构建了方差风险溢价，分析其对50ETF收益率的影响。研究发现，隐含高阶矩与50ETF收益率之间存在显著的相关性。一方面，隐含波动率指数和收益率之间的负相关性为中国市场可能存在杠杆效应和波动率反馈效应提供了一定的实证依据。另一方面，隐含偏度指数与收益率之间的正相关性在一定程度上说明了当市场投资者更偏好右偏资产时，由于这类资产被高估，可能导致负收益。此外，本文还发现已实现高阶矩与隐含高阶矩之间存在显著的相关性，这表明50ETF期权隐含信息对50ETF收益率的方差和偏度具有一定的解释作用。对于方差风险溢价，笔者发现市场平静期间，隐含波动率通常高于已实现波动率，表明中国投资者大部分时间在规避风险，并且愿意为对冲风险支付费用。同时，研究发现中国市场的方差风险溢价对收益率的影响并不显著。

07d8b73b6b3a126084e933814ebd3169

综上所述，投资者在制定投资策略时应充分考虑期权隐含的高阶矩风险信息，并合理配置资产。同时，监管部门也应关注期权隐含的高阶矩风险，以便更好地管理衍生品市场的风险。

参考文献

［1］ANAGNOUI，BEDENDOM，HODGESSD，etalTherelationbetweenimpliedandrealisedprobabilitydensityfunctions［J］SSRNElectronicJournal，2002

［2］ANDERSENTG，BOLLERSLEVTAnsweringtheskeptics：Yes，standardvolatilitymodelsdoprovideaccurateforecasts［J］InternationalEconomicReview，1998，39（4）：885-905

［3］BAHRABImpliedrisk-neutralprobabilitydensityfunctionsfromoptionprices：Acentralbankperspective［J］ForecastingVolatilityintheFinancialMarkets（ThirdEdition），2007：201-226

［4］BAKSHIG，KAPADIAN，MADANDStockreturncharacteristics，skewlaws，andthedifferentialpricingofindividualequityoptions［J］TheReviewofFinancialStudies，2003，16（1）：101-143

［5］BALITG，MURRAYSDoesrisk-neutralskewnesspredictthecross-sectionofequityoptionportfolioreturns？［J］JournalofFinancialandQuantitativeAnalysis，2013，48（4）：1145-1171

［6］BLISSRR，PANIGIRTZOGLOUNTestingthestabilityofimpliedprobabilitydensityfunctions［J］JournalofBankingandFinance，2002，26（2-3）：381-422

［7］BLACKF，SCHOLESMThepricingofoptionsandcorporateliabilities［J］JournalofPoliticalEconomy，1973，81（3）：637-654

［8］BOLLERSLEVT，TAUCHENG，ZHOUHExpectedstockreturnsandvarianceriskpremia［J］TheReviewofFinancialStudies，2009，22（11）：4463-4492

［9］CHANGBY，CHRISTOFFERSENP，JACOBSKMarketskewnessriskandthecrosssectionofstockreturns［J］JournalofFinancialEconomics，2013，107（1）：46-68

［10］HARVEYCR，SIDDIQUEAConditionalskewnessinassetpricingtests［J］TheJournalofFinance，2000，55（3）：1263-1295

［11］HARVEYCR，SIDDIQUEATime-varyingconditionalskewnessandthemarketriskpremium［J］ResearchinBankingandFinance，2000，1（1）：27-60

［12］JIANGGJ，TIANYSExtractingmodel-freevolatilityfromoptionprices：AnexaminationoftheVIXindex［J］TheJournalofDerivatives，2007，14（3）：35-60

［13］JIANGGJ，TIANYSThemodel-freeimpliedvolatilityanditsinformationcontent［J］TheReviewofFinancialStudies，2005，18（4）：1305-1342

［14］JONDEAUE，ZHANGQ，ZHUXAverageskewnessmatters［J］JournalofFinancialEconomics，2019，134（1）：29-47

［15］CARRP，MADANDTowardsatheoryofvolatilitytrading［J］Volatility：Newestimationtechniquesforpricingderivatives，1998（29）：417-427

［16］CARRP，WULVarianceriskpremiums［J］TheReviewofFinancialStudies，2009，22（3）：1311-1341

［17］CHRISTOFFERSENP，JACOBSK，CHANGBYForecastingwithoptionimpliedinformation［J］HandbookofEconomicForecasting，2013，2（A）：581-656

［18］CHRISTOFFERSENP，HESTONS，JACOBSKTheshapeandtermstructureoftheindexoptionsmirk：Whymultifactorstochasticvolatilitymodelsworksowell［J］ManagementScience，2009，55（12）：1914-1932

［19］QIAOF，XUL，ZHANGX，etalVarianceriskpremiumsinemergingmarkets［J］JournalofBanking&Finance，2024（167）：107259

［20］HESTONSLAclosed-formsolutionforoptionswithstochasticvolatilitywithapplicationstobondandcurrencyoptions［J］TheReviewofFinancialStudies，1993，6（2）：327-343.

［21］丛明舒中国场内期权市场研究——基于中美关于期权隐含方差的差异［J］金融研究，2018（12）：189-206

［22］李志勇，余湄，汪寿阳方差风险溢价和收益率预测：来自上证50ETF期权市场的证据［J］系统工程理论与实践，2022，42（2）：306-319

［23］田凤平，杨科我国商品期货的无模型隐含方差与方差风险溢价研究基于豆粕和白糖的分析［J］系统工程理论与实践，2021，41（8）：2015-2029

［24］王琳玉，倪中新，郭婧上证50ETF隐含高阶矩风险对股票收益的预测研究［J］统计研究，2020，37（12）：75-90

［25］郑振龙，孙清泉，吴强方差和偏度的风险价格［J］管理科学报，2016，19（12）：110-123