巧妙追问促进小学生数学深度学习的实践与认识

［摘 要］ 研究者以“容积最大是多少”问题的探究为例，具体阐述了追问在常规课堂中的实践。教师要通过巧妙追问，让学生的深度学习自然发生，培育学生数学理性精神。

［关键词］ 追问；深度学习；容积

近年来，数学教师对深度学习的教学研究愈发关注，问题引导交流对话是教学中常见的组织形式，以追问为手段促进小学生数学深度学习已成为数学教师十分关注的研究之一。

一、科学理解深度学习与追问的内涵与价值

数学学习中学生“肤浅”学习的情况时有发生，最常见的表现就是死记硬背知识和缺乏应用知识的能力。这种现象与长期课堂内的“师讲生听”的被动教学模式有很大关系，存在教学效率低的问题，应及时纠正。

1. 追问的内涵与价值

追问是针对某个内容或问题，为了使学生理解或掌握得更清楚、更透彻、更深入，教师在一次提问后再次提问，且不断发问，直至问题得到解决。这样“穷追不舍”的追问可以让学生主动思考、深入探索、深度探讨，从而在深度学习中发展思维，最终实现对数学知识本质的深度理解与感悟。

2. 深度学习的内涵与价值

深度学习是基于理解性学习的批判性学习，将新知自然融入学生已有认知结构去解决问题。事实上，深度学习是相对于被动的浅层学习而言，是在浅层学习之上的学习方式的转变、思维水平的进阶及知识结构的延伸，最终使学生实现在已有知识经验基础上的自主建构，促进完整知识体系的形成。

学生的思维水平与数学素养可以通过训练得以提高，从对追问与深度学习的内涵与价值分析不难看出，巧妙追问可以改变被动的浅层学习模式，引导学生拾级而上地思考、探索，最终在深度学习中发展思维，提升素养。当然，不是任何情况下任何形式的追问都能促进学生深度学习。

二、追问在常规课堂中的实践

笔者以“容积最大是多少”这一问题的探究为例，具体阐述如何让有效追问促进学生深度学习，促使学生更加深入地思考、建构。

1. 课前慎思

本题是“整理与复习”单元中“应用广角”的一道具有探究性的习题，如果教师不对题目进行延展，仅是解题了事，那么学生很难真正意义上达成“在动手实践中深度探索与交流”这一目标。教师该如何设计才能水到渠成地达成发展学生数学思维的目标呢？（问题如图1）

在设计教学的过程中，教师要以“动手做纸盒”的活动为主线，以巧妙且适时的追问为载体，引导学生深入思考、深度探究和深入探讨，充分发挥问题的教学价值，使“容积最大是什么”得到解决，让学生切实感悟不完全归纳的推理方法，从而在深度思考中实现低阶思维朝着高阶思维的自然转变。

2. 教学过程

（1）首次追问，营造逐步思考的氛围

师：如图1，这个长方体纸盒的长是多少厘米？宽呢？高呢？（学生取出早已准备好的长方形纸片，开始动手实践）

生1：长为26-4-4=18（厘米），宽为18-4-4=10（厘米），高4厘米。

师：容积呢？

生2：18×10×4=720（立方厘米）。

师：非常好！现在我们来变一变，把这张纸边长改成“9厘米的正方形纸”，其余条件不变，你们会不会？

生3：不就是换一张纸折吗？折法还是一样的。

师：那剪去一个边长是x厘米的小正方形，该如何表示这个长方体的长、宽、高呢？

生4：长和宽一样，都是（9-2x）厘米，高x厘米。

师：假如剪去的小正方形边长是2厘米呢？又该如何计算容积呢？

生5：折出的长方体纸盒长与宽均为5厘米，高2厘米，容积为50立方厘米。

师：是不是可以这样说“折出的无盖长方体纸盒的最大容积是50立方厘米”？（学生陷入思考）

生6：不一定吧！如果剪去的小正方形的边长不是2厘米的话，容积也会随之变化，超过50立方厘米也是可能的。

评析：强调实践操作既是强化实践能力的策略，又是发展学生思维的方法。学生通过动手操作解决问题之后，教师适时变化原题，并以追问的形式引导学生进入思考状态，并得出“剪去的小正方形边长可变且不确定”的结论，为后续的深入探索做足准备。

（2）梯度追问，促成渐次深入的探索

师：如果从边长为9厘米的正方形纸片四个角各剪去一个小正方形（边长为整厘米数），那剪去小正方形的边长可能是多少厘米？折出的无盖长方体的容积呢？

生7：当小正方形的边长为5厘米时，两边就需要10厘米了，肯定不够。因此，边长有可能是1厘米、2厘米、3厘米或4厘米。

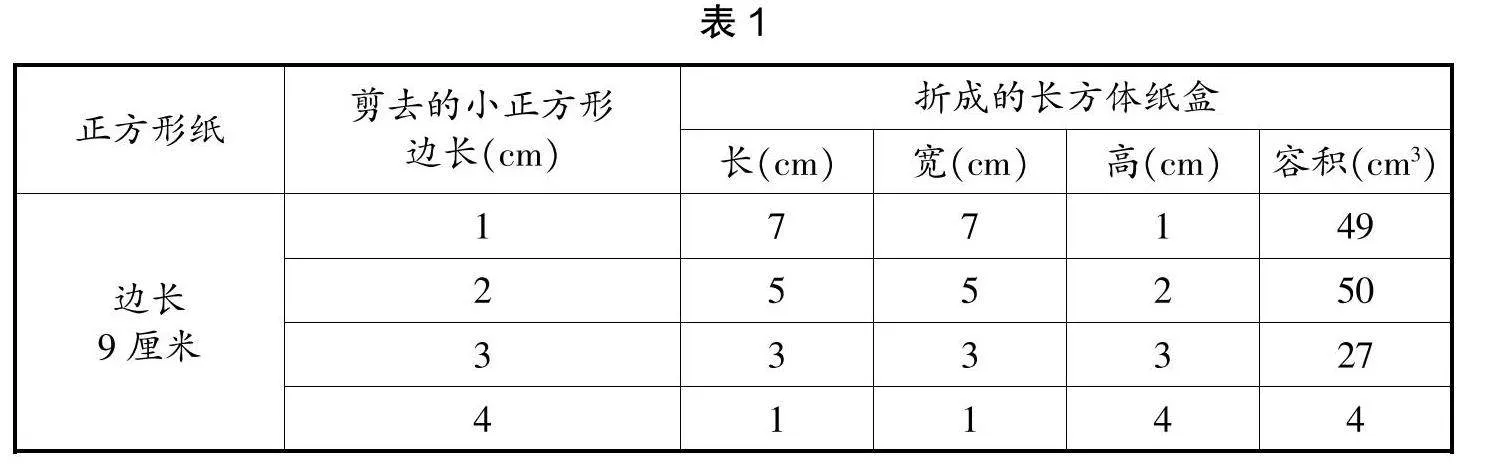
师：组内四人一组，各选择其中一种情况去制作无盖长方体纸盒，并计算容积。（学生投入活动，在合作交流后生成表1）

师：观察表1，容积最大只能是50立方厘米，对吗？

生8：是的，这就是最大的。

生9：不一定！小正方形的边长可以是小数。

生10：我也赞同生9的说法，边长的情况太多了。

师：根据以表1的数据无法确定折出的长方体纸盒容积最大是多少。

评析：教师通过创意变化习题，让学生去分析探索，最终在合作学习中获取数据，验证猜想。这样的追问过程不仅可以磨砺学生的实践能力，还能为学生后续深入探究积累足够的经验。

（3）深入追问，促成更加完善的思路

师：如果在一个边长为9厘米的正方形纸片上的四个角各剪去一个正方形，然后折出的长方体容积是多少？你们觉得这个问题有何注意点？

生11：可以发现“边长是整厘米数”这个条件没有了。

师：如果小正方形边长为0.5厘米，容积是多少？（学生在探究后很快得出答案）

师：继续探索会怎样？有没有困难？

生12：会看到“无数个小数”，我该如何选择？

师：是啊！显然猜测与尝试并不是毫无章法。（学生思考后很快发现，50立方厘米是一个界限，因此得出“可以选择2点几这个小数”的想法）

师：真是有意义的发现，那就顺势摸索吧！（学生边探索边交流，得出最大容积的小正方体边长为1厘米到2厘米之间，从而又一次开展合作学习，生成了表2所示的结论）

师：你们能发现什么？

生13：数值“1.5”可能是容积最大的时候。

师：还有其他观点吗？

生14：表2中都是一位小数，也有可能是两位小数或三位小数。

生15：因为1.4到1.5是上升，而1.5到1.6是下降，因此我认为可以选择1.4到1.6之间的两、三位小数继续研究。（在教师默认后，学生进行分工合作，并得出结论“当剪去小正方形边长为1.5厘米时折成的无盖长方体纸盒容积最大”。接着教师呈现图2所示的关系图，学生畅所欲言，一一阐述图中各个量及关系）

师：我们不妨再深入想一想，若小正方形的边长为1.5厘米，它与大正方形的边长有何关系？

生16：。

师：不错，若剪去小正方形边长为大正方形的，则可折出一个容积最大的无盖长方体纸盒。在以后高中阶段的学习中我们就可以证明该结论是正确的。

师：回顾前面的探索过程，你们有什么想法或体会吗？

生17：我觉得尝试计算探索答案的过程十分有趣。（学生七嘴八舌地阐述自己的心得体会）

师：很好，当我们面对数学问题时，需要……

评析：探究性学习离不开猜测、验证和归纳，以上环节中，教师以追问的方式为学生指明探索的方向，让学生亲历探索过程，最终自主归纳出结论，切实感受数形结合思想，使数学视野更宽广。

（4）自主追问，让思维朝着最深处延伸

师：一直是老师在追问，现在换成你们追问，如何？（学生思考）

生18：利用边长是9厘米的正方形纸制作出的无盖长方形纸盒的最大容积一定是54立方厘米吗？（教室里瞬间爆发出大笑声）

师：你们觉得生18在明知故问，所以有了这样的反应，对吗？下面我们一起来看这样一个问题。（课件呈现问题，即生18抛出的问题，学生开始仔细研究）

生19：这个问题比之前的少了一个条件，即“剪去四个角”。

师：不错，在不浪费纸张的情况下，制作的无盖长方体纸盒的容积是多少？这个问题就留到课后大家继续探索。

评析：问题解决后学生的思维处于十分活跃的状态，此时教师通过追问引导学生自主追问，可以引发更具思维含量的好问题、真问题。当生18抛出问题后，不少学生认为是明知故问，事实上却是从前面探索衍生出来的深度思维的问题。从课后学生的状态不难发现，正是学生自主追问，才引发了后续问题，将课堂延伸到了课后，并生成了新的、高质量的数学问题，让学生的深度学习延展开去。

3. 课后反思

（1）追问要做到“胸中有丘壑”

数学课堂是动态生成的，追问的过程更是如此，巧妙追问可以让数学课堂“动且不乱”“动却有序”。为了让有效追问促进学生深度学习，教师需要明确教学目标，切实把握一节课的重点和难点，以达到“问即有效”的效果。本课中，如此流畅的教学设计源于教师对教材、教学内容尤其是具体学情的充分把握，这样才能从设问处展开层层追问，让学生跟着问题的引导逐步走向探索的高潮，这才是真探索、高质量的数学课堂。

（2）追问要做到“万紫又千红”

追问的形式并非一成不变，很多时候应是“万紫又千红”。在课堂中，如果教师采用单一追问的形式，势必导致学生兴趣逐渐减弱、启而不发等现象。教师要从一节课的目标与性质出发，根据教学环节的实际需求灵活追问，从而打开学生的思维之门，促进学生在深度学习中进行自身认知的再创造，完善认知结构，发展理性精神。本课中，教师在教学的各个环节采用不同的追问方式，或激发思考，或引发探索，或促成思路，或引导自主追问，让学生在角色体验中收获丰富的、有意义的学习体验，最终使深度学习水到渠成。

总之，巧妙而恰当的追问是教师教学机智的体现。在教学中教师要不断完善追问艺术，让学生的深度学习自然发生，让数学课堂生机盎然，进而培育学生数学理性精神。