基于PLAXIS的注浆体与锚板协同锚固模型分析

摘 要：【目的】对协同锚固条件下注浆锚板拉拔模型进行有限元模拟，研究注浆体与锚板协同锚固控制前后锚板周围土体的变形、破裂面的变化以及锚固力的增长规律。【方法】采用PLAXIS有限元软件，并基于Tresca屈服准则的硬化土（HS）模型，建立不同试验条件下的锚板拉拔有限元分析模型，并对计算得到的位移云图、塑性点分布图及锚固力增长曲线等进行对比分析。【结果】对比锚板与注浆体协同锚固前后的位移云图可知，协同锚固后的锚板在拉拔过程中对土体的影响范围明显扩大；对比不同注浆体直径的试验发现随着注浆体直径的增加，锚板上方土体减少，锚固影响区域的形态逐渐由三角形发展为梯形；对比协同锚固前后的锚固力增长数据与位移云图可知，锚固力增加的同时，塑性区范围也出现扩大情况。【结论】研究结果表明，运用浆锚协同位移控制方法可提升锚板的锚固性能，为浆-锚协同锚固位移控制方法的推广应用提供了试验依据。

关键词：锚板；PLAXIS；注浆体；浆-锚协同；拉拔试验

中图分类号：U416.1 文献标志码：A 文章编号：1003-5168（2024）21-0067-06

DOI：10.19968/j.cnki.hnkj.1003-5168.2024.21.014

Analysis of Synergistic Anchoring Model of Grouting and Anchor Plate Based on PLAXIS

HE Yilin GAO Wenda

（Changjiang River Scientific Research Institute， Wuhan 430014， China）

Abstract： [Purposes] Finite element simulation of the grouted anchor plate pullout model under cooperative anchoring conditions is carried out to study the deformation of the soil around the anchor plate before and after the control of cooperative anchorage between the grouting and the anchor plate， the change of the rupture surface as well as the growth law of the anchoring force. [Methods] Using PLAXIS finite element software and hardened soil （HS） model based on Tresca yield criterion， the finite element analysis model of anchor plate pullout under different test conditions was established， and comparative analyses were carried out based on the computed displacement cloud， plasticity point distribution map and anchoring force growth curve. [Findings] Comparing the displacement cloud diagrams before and after the cooperative anchoring of the anchor plate and the grouting， it can be seen that the scope of influence on the soil body of the anchor plate after cooperative anchoring in the pulling process is obviously enlarged; comparing the tests with different diameters of the grouting， it is found that with the increase of the diameter of the grouting， the soil above the anchor plate decreases， and the morphology of the area of influence of the anchoring gradually develops from a triangular shape to a trapezoidal shape; comparing the data of the growth of the anchoring force before and after the cooperative anchoring with the displacement cloud diagrams， the increase in the anchor force is accompanied by an expansion of the range of the plastic zone; comparing the anchoring force growth data and displacement cloud diagrams before and after synergistic anchoring， the anchoring force increases while the plastic zone range also appears to be enlarged.[Conclusions] The research results show that the use of slurry-anchor cooperative displacement control method can improve the anchoring performance of the anchor plate， which provides a test basis for the popularization and application of the slurry-anchor cooperative anchoring displacement control method.

Keywords： anchor plate; PLAXIS; grouting body; pulp-anchor synergy; pull-out test

0 引言

预应力伞型锚的锚固力由初始较小增长到峰值会经历较长的位移过程，而注浆体与周围土体的剪应力在伞型锚抗拔力达到峰值前即会失效，要实现浆-锚协同，必须在准确掌握浆体和伞型锚单独抗拔规律的基础上，通过提前张拉伞型锚，预留与注浆体发挥最大抗拔力相适应的位移，以及注浆对锚固效应的叠加效应，并将临时性快速抢险措施和永久性修复相结合。

锚杆（索）、注浆体以及拟加固岩土体的界面力学特性一直是锚固技术研究的热点。近年来，黄明华［1］、应志民［2］等结合模型试验和理论推导认为协同受力作用下的界面阻力可用指数形式表达；张季如等［3］提出了锚固单元体侧阻力双曲线模型表达形式；张培胜等［4］则做了进一步归纳，提出了复合指数−双曲线模型，并进行了锚固段界面应力的解析解推导；郭锐剑等［5］进一步从界面的本构模型入手，认为其可描述为黏结−软化−滑动；Ren 等［6］根据试验成果拟合认为锚固界面剪应力和位移可用三线性拟合；尤春安［7］、蒋忠信［8］也运用相关理论各自建立了锚固体的全过程剪应力表述模型。

后注浆是桩基工程中的热点问题，对浆-锚协同研究有一定的借鉴意义。张晓华等［9］通过后注浆载荷试验，研究在后注浆过程中注浆压力、注浆量、桩顶位移的实时响应规律，探究桩底复合式后注浆对桩承载特性的影响；赵春风等［10］通过开展单桩抗压室内试验，研究桩侧后注浆量对单桩抗压承载性能的影响。在注浆体的材料方面，张乐文等［11］研究发现常规的水泥砂浆凝结时间较长，强度发挥较慢，不能很好适应岩土工程复杂多变的现场条件等；石明生等［12］以高聚物注浆锚杆为对象，对高聚物锚固体与粉土间的黏结性能进行了大量试验，详细研究了锚固体直径、密度、长度对黏结强度的影响。

土体工程锚固结构中，在注浆体填充锚杆与土体间空隙、并与锚杆融为一体之前的较长时间段，锚固效果无法体现，且在发挥效用后，锚固力取决于锚杆、注浆体和土体三者中的最薄弱面，即便新材料的应用，也不存在锚固力叠加效应问题。伞型锚作为一种新型锚固结构，施加预应力端部锚板张开后，可即刻产生锚固力，达到快速抢险的目的；后注浆可增加锚固结构和土体的接触面积，与锚固预应力呈叠加关系，两者先后发挥效应，并在融为一体后协同受力且变形协调，在土体工程永久性修复中共同发挥作用，但现有研究在解释该协同受力机制和变形协调方面存在理论缺失，需开展进一步研究。

PLAXIS软件是20世纪70年代由荷兰代尔夫特工业大学研发的，最初用于计算荷兰的软土地基上的河堤问题，后来经过不断地发展，PLAXIS广泛应用于各种岩土工程项目，并成为重要的数值分析工具［13］。刘红军等［14］利用PLAXIS对某基坑工程进行数值计算，计算的地表水平位移结果与实测值吻合较好。田利勇等［15］使用PLAXIS对4种不同的板桩结构进行数值模拟，得到了各种板桩结构的位移变形与桩侧土压力分布情况。朱彦鹏等［16］使用PLAXIS软件，对比分析了锚托板的计算方法，分析了边坡的位移、框架立柱的内力，并采用实测数据对比，证明了模拟结果的合理性。

综上所述，通过循环张拉进行位移控制可实现锚板与注浆体的锚固力高效叠加，且叠加后锚固力大于注浆体与锚板的锚固力之和，其与浆锚协同后的拉拔影响区域明显相关。故本研究采用PLAXIS有限元软件，进一步对锚板拉拔模型试验进行深入模拟，分析浆锚协同条件下的锚板周围土体变形、锚板上拔影响范围变化以及破裂面形态变化等情况。

1 注浆体与锚板协同锚固有限元模型参数选取

为了减少计算量，节约时间，利用模型的对称性，模仿室内试验取该锚板的一半进行建模分析，取锚板长度为20 cm，宽度为10 cm，厚度为2 cm。室内试验的位移加载方式通过软件内的“添加位移”功能为锚板添加z轴正方向的位移实现，土体表面的荷载可使用“添加面荷载”的功能在土体上表面添加z轴负方向的均布荷载实现。PLAXIS软件采用10节点四面体单元划分网格，并对锚板附近网格进行优化，网格划分如图1所示。锚板与锚杆连接处设置为刚性连接。PLAXIS中可采用界面单元模拟锚板与土之间的接触面，由于物理模型中锚板下表面在上拔位移施加以后，锚板与土将迅速分离，据此设置底面接触界面，界面设置采用折减法，折减系数根据经验选取[Rinter=0.667]，土体模型底面边界设置为全自由度约束完全固定边界，模型上边界设置为自由边界，左右两侧界为法向约束边界。在计算前的“分阶段施工”步骤，锚杆拉拔之前应设置一初始阶段，并生成土体初始地应力。

上述试验在有限元软件PLAXIS 中计算时，采用基于Tresca屈服准则的硬化土（HS）模型。HS模型是Schanz等［17］在邓肯-张模型基础上提出的双曲线弹塑性模型，该模型考虑了土体剪切硬化和压缩硬化，可以反映土体刚度的应力相关性，适用于描述多种土类的变形破坏特征。

土体硬化模型包含11个参数，其中刚度参数有标准三轴排水试验割线刚度[Eref50]、侧限压缩试验切线刚度[Erefoed]、卸载/重加载刚度[Erefur]、刚度的应力相关幂指数[m]、卸载-重加载泊松比[vur]、刚度参考应力[Pref]、正常固结侧压力系数[Knc0]；强度参数为有效黏聚力cref、有效摩擦角φ、剪胀角[ϕ]及破坏比[Rf]。

其中HS模型参数的取值，土体强度参数按照土的物理力学参数确定即可。刚度参数则依据Plaxis手册［18］，刚度参考应力[Pref]建议值为100 kPa；同时[Eref50=Erefoed、Erefur=3～5Eref50、Es1−2=Erefoed]，其中[Es1−2]为土体压缩模量。对于正常固结侧压力系数可参照[Knc0=1−sinφ∙]计算取值；对于黏土，剪胀角[ϕ]可取值为0。

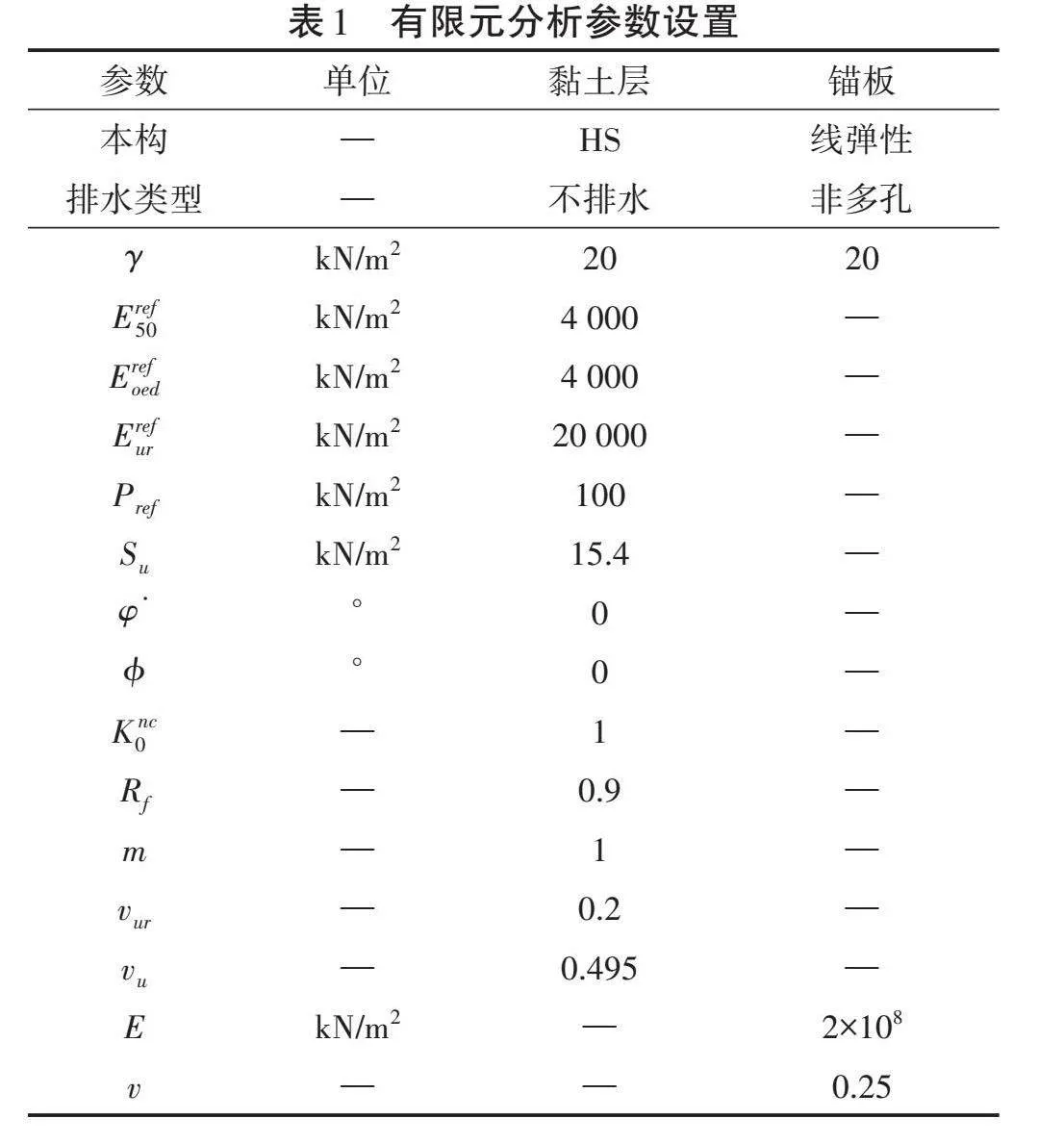
综上所述，HS模型参数取值见表1，表1中[vu]为土体不排水泊松比，[v]为锚板泊松比。

2 浆-锚协同锚固效果数值分析

2.1 数值计算方案

为了探明浆-锚协同锚固位移控制方法作用前后，锚板周围土体变形、锚板上拔影响范围变化以及破裂面形态变化等情况，基于室内模型试验结果，建立锚板拉拔有限元分析模型，模型条件见表2。

其中，锚板与注浆体协同锚固方法具体为：首先，通过试验得到注浆体的拉拔荷载—位移曲线，并获取注浆体达到极限锚固力时对应的张拉位移；然后，按极限锚固力对锚板进行循环张拉，直至张拉位移小于注浆体的极限锚固力对应的张拉位移。

经过浆-锚协同控制后的锚板与注浆体接触时，锚板已经具有一定的锚固力，注浆体也在此时发挥锚固作用，在注浆体锚固力达到极限时，锚板的锚固力也达到极限，从而使得注浆体和锚板能够协同提供锚固力。

下文中有限元模型通过预先为锚板设置指定位移来模拟协同锚固位移控制方法的实施。其中，指定位移根据试验得到的注浆体拉拔荷载—位移曲线上极限锚固力对应的极限位移取值。

2.2 协同锚固对拉拔力的影响规律

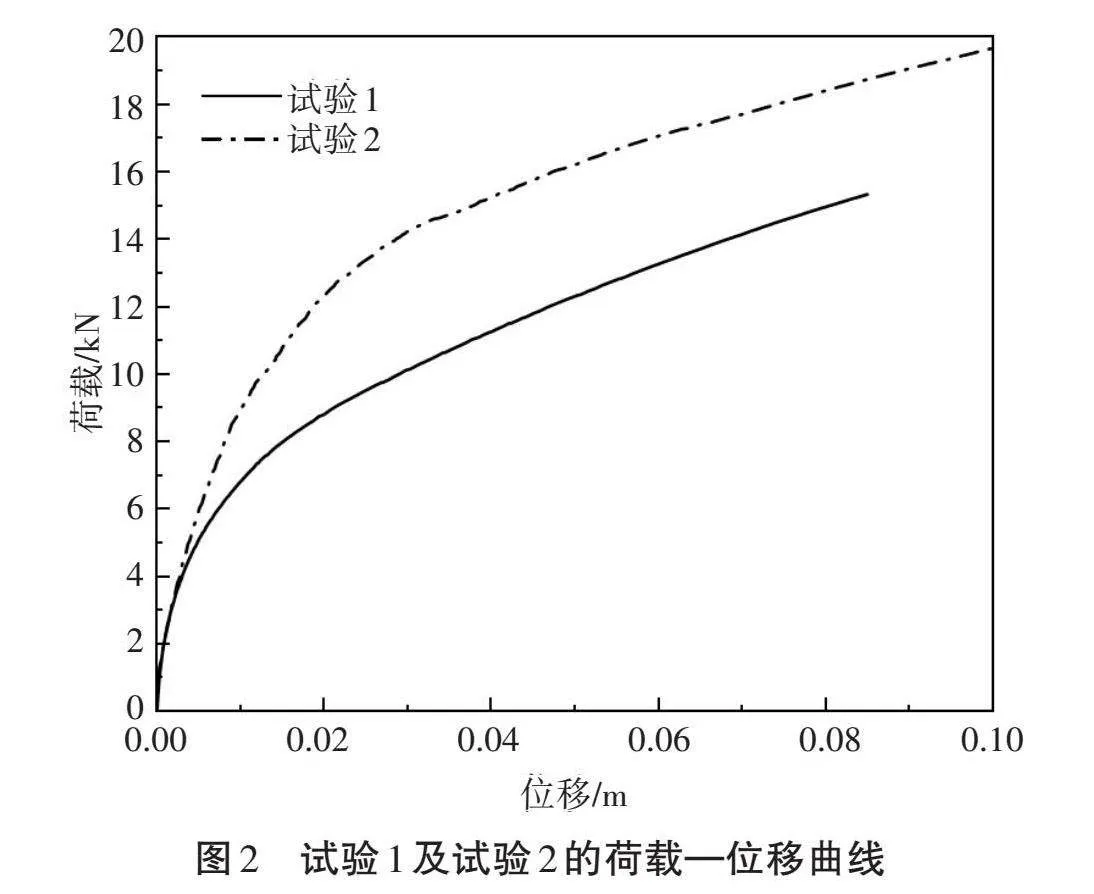
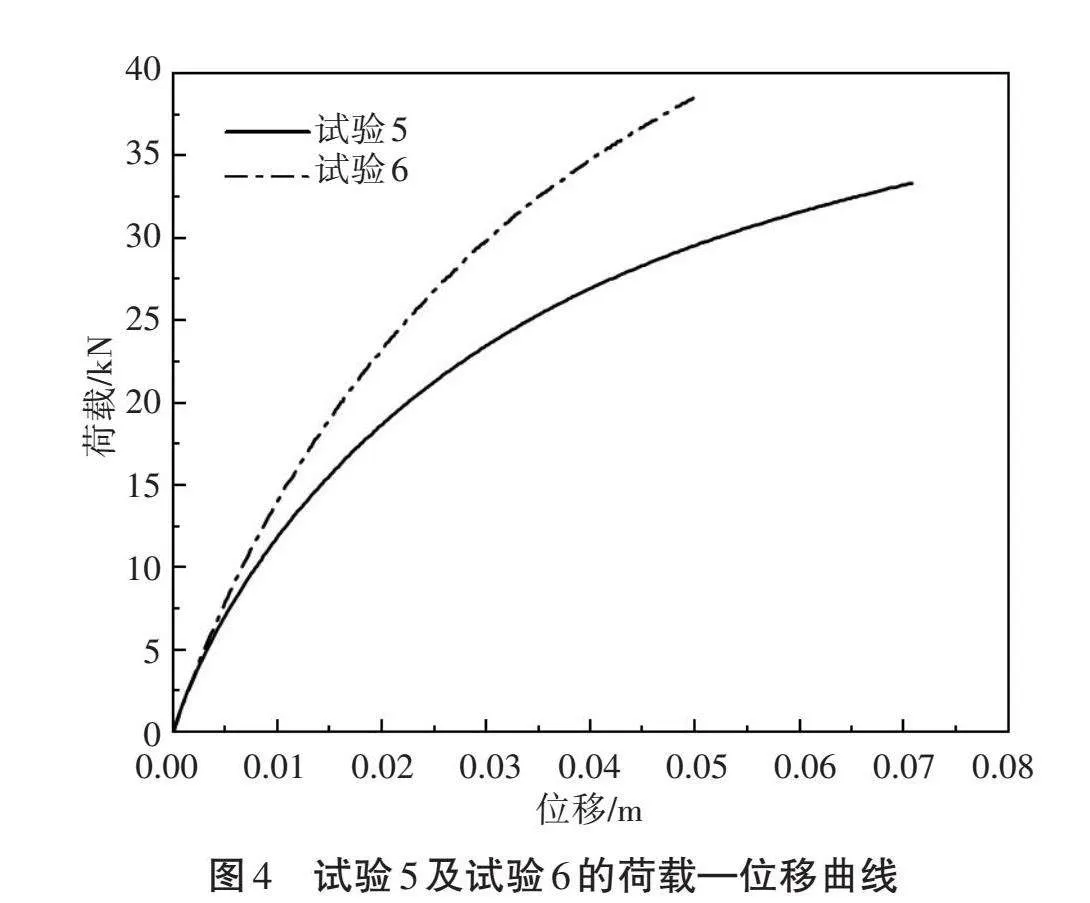
整理后处理阶段的输出数据并绘制注浆锚板在预张拉前后的拉拔荷载—位移曲线，包括注浆体直径50 mm的试验1、试验2，注浆体直径100 mm的试验3、试验4，注浆体直径150 mm的试验5及试验6，各试验曲线如图2、图3和图4所示。

由图2知，试验2在经过协同锚固位移控制的注浆锚板抗拔力快速增长阶段更长，直到位移加载至30 mm时，注浆锚板锚固力达到14 kN，并且经过抗拔力缓慢增长阶段，最终注浆锚板的最大抗拔力

达到19.17 kN；未经过协同锚固位移控制的注浆锚板试验1，抗拔力快速增长阶段出现在1～20 mm位移之间，并在该阶段锚板锚固力达到8 kN，并经过缓慢增长阶段，锚板的最大锚固力达到15.34 kN。对比两条曲线的锚板锚固力发展阶段以及最大锚固力，可知经过协同锚固位移控制处理的锚板能够发挥更大的锚固力。

由图3可知，在位移加载初期锚固力快速增长时期，试验3及试验4二者荷载—位移曲线很接近，在位移加载至20 mm时，经浆-锚协同锚固位移控制的注浆锚板锚固力相较于未经过位移控制的注浆锚板锚固力高出约2.5 kN，继续加载位移，二者均进入到锚固力缓慢增长阶段，并且两条曲线的锚固力差值逐渐增大，在位移加载至60 mm时，二者的差值增加至5 kN，根据上述压力型注浆锚杆试验中所得直径100 mm注浆体极限锚固力为1.5 kN，可见试验4中经过协同锚固位移控制后，锚板锚固力出现小幅增长。

由图4可知，位移加载初期试验5及试验6中的锚板锚固力发展阶段存在差异。其中试验5在0～25 mm的位移区间内为锚固力快速增长阶段，并在位移加载至25 mm时锚板锚固力达到20 kN，然后锚板锚固力进入缓慢增长阶段；试验6在位移加载初期锚固力已经开始快速增长，并且在位移达到50 mm时，锚固力达到38.58 kN，而同一位移对应的试验5中的锚板锚固力为29 kN，差值接近10 kN。

2.3 锚周土体变形与破坏特征

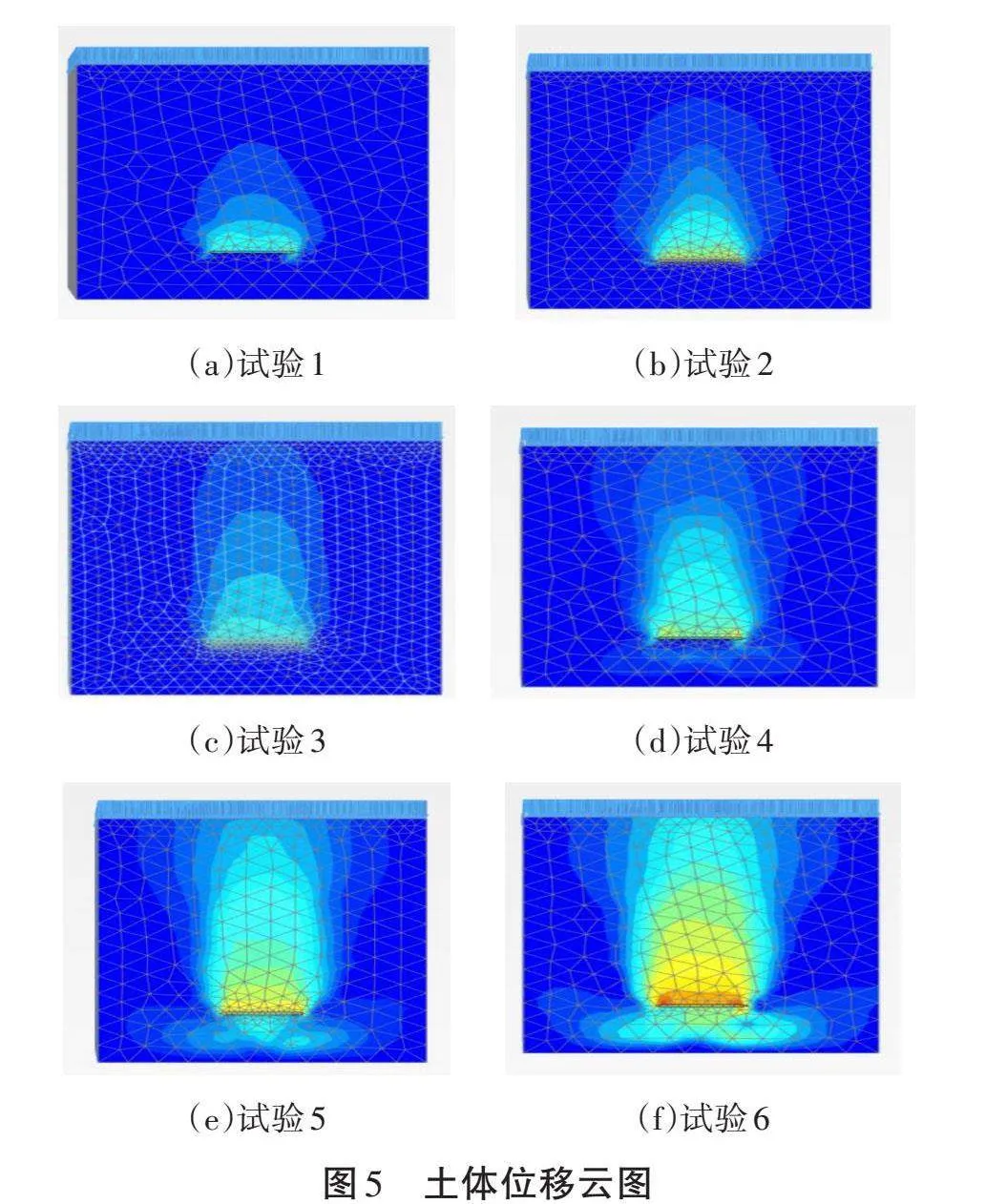
按上述有限元试验方案建立模型，并定义施工阶段，注浆锚板在上拔过程中的位移云图、塑性点图分别如图5和图6所示。

其中图5（a）、5（c）、5（e）分别为注浆体直径50 、100、150 mm的未经过预张拉的注浆锚板位移云图，图5（b）、5（d）、5（f）分别为注浆体直径50、100、150 mm的经过预张拉的注浆锚板位移云图。

从图5可以看出，锚板在上拔过程中，其边缘处及锚板上部均出现了土体位移，其中图5（a）、5（b）中注浆体直径为50 mm，而锚板的长边尺寸为200 mm，注浆体截面直径占锚板长边的1/4，锚板上方存在一近似三角形的压密区，在持续的上拔过程中锚板在土中的影响范围逐渐增大，位移由锚板边缘向外延伸，最终形成一封闭曲面。图5（c）、5（d）中注浆体直径为100 mm，可见该试验条件下锚板位移分布范围更广，位移面由锚板两侧向上延伸，且最外侧位移面与锚板所在平面夹角近似π/4+φ/2，延伸至一定范围后开始向上延伸，直到土体顶部，图5（e）、5（f）中注浆体直径为150 mm，该组试验中土体位移分布更加广泛，且靠近锚板一定范围内的土体在受到挤压后，开始沿锚板边缘向锚板底部流动，从位移云图上来看，更大的注浆体直径试验，锚板在拉拔过程中能调动更多的土体共同承受上拔力。

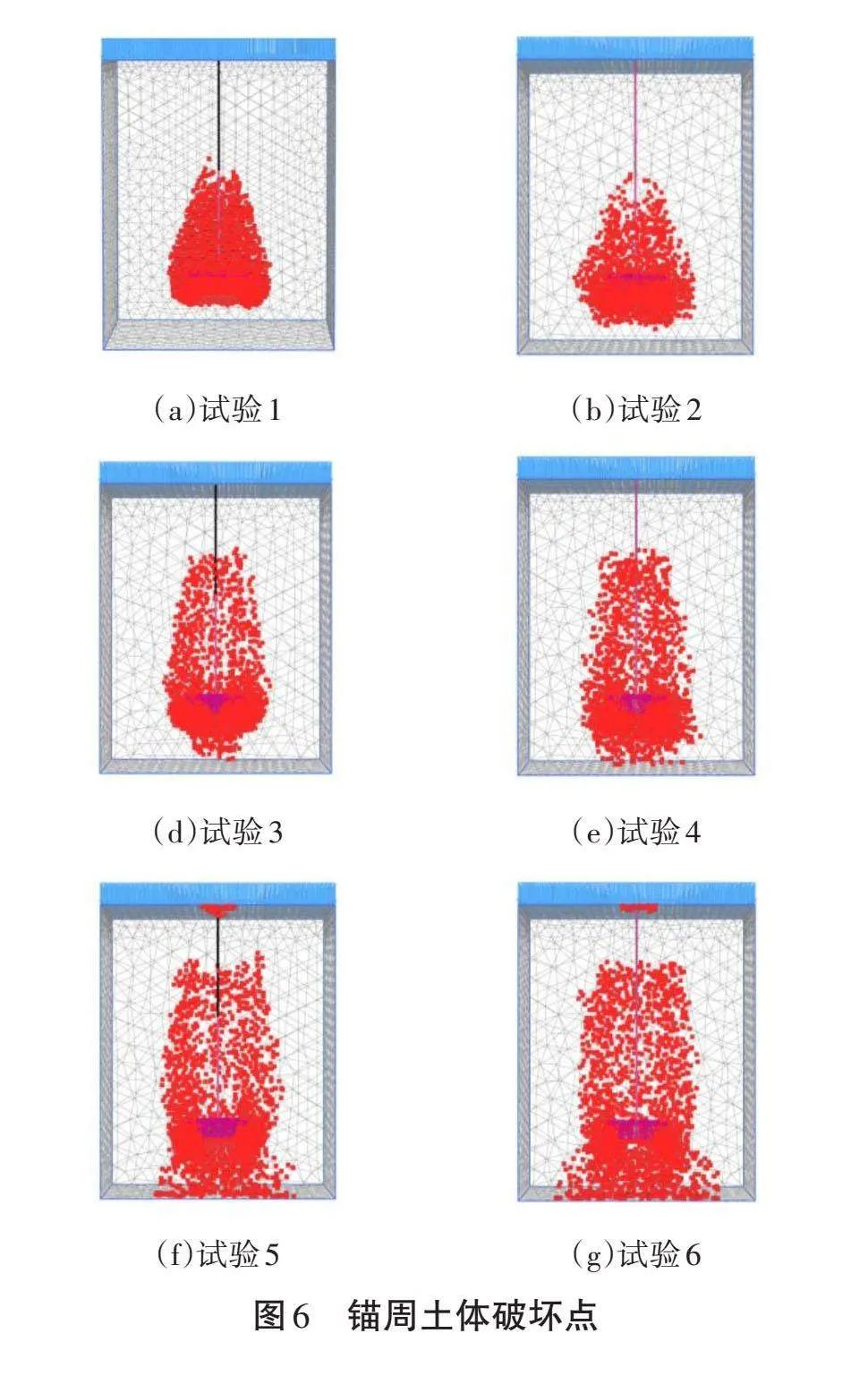
PLAXIS软件可以根据预先设置的本构模型，判定岩土体中各种塑性点的分布，其中破坏点（Failure points）可以直观显示基础上拔承载时岩土体内发生塑性破坏区域的点，其中，破坏点是指位于本构模型破坏包络面上的点，即违背摩尔-库仑屈服准则的点。

经过协同锚固位移控制的注浆锚板试验和未经过协同锚固位移控制的注浆锚板试验破坏点分布如图6所示。在拉拔过程开始阶段，锚板上部靠近锚板的区域以及锚板边缘产生塑性区域，并沿π/4+φ/2的角度，约57°倾斜角的方向向侧方发展，在延伸一定距离后继续向上发展，并逐步向注浆体靠拢，最终形成如图6所示的破裂面形态。

结合图4、图3及图2中的协同锚固前后的注浆锚板拉拔荷载—位移曲线以及图6中的协同锚固前后注浆锚板的破坏点分布，可以看出锚固力大小与塑性区范围呈正相关，锚固力较大的工况对应的塑性区范围更大。

3 结论

本研究采用有限元软件PLAXIS对锚板拉拔模型试验进行模拟，分析了浆-锚协同条件下的锚板周围土体的破坏特征、锚板上拔影响范围变化以及破裂面形态变化等情况，得出以下结论。

①对比锚板与注浆体未协同锚固的情况，浆锚协同锚固后的锚板在拉拔过程中对土体的影响范围明显扩大。

②随着注浆体直径的增加，锚板上方土体减少，锚固影响区域的形态逐渐由三角形发展为梯形。

③对比协同锚固前后的锚固力增长数据与位移云图，锚固力增加的同时，塑性区范围也出现扩大情况。

参考文献：

［1］黄明华，周智，欧进萍.拉力型锚杆锚固段拉拔受力的非线性全历程分析［J］.岩石力学与工程学报， 2014， 33（11）： 2190-2199.

［2］应志民，张洁，尚岳全.锚杆荷载−位移曲线的指数函数模型研究［J］.岩土力学，2005，26（8）： 1331-1334.

［3］张季如，唐保付.锚杆荷载传递机理分析的双曲函数模型［J］.岩土工程学报，2002，24（2）： 183-192.

［4］张培胜，阴可.拉力型锚杆锚固段传力机理的全过程分析方法［J］.地下空间与工程学报，2009，5（4）：716-723.

［5］郭锐剑，谌文武，段建，等.考虑界面软化特性的土层锚杆拉拔受力分析［J］.中南大学学报（自然科学版），2012， 43（10）： 4003-4009.

［6］REN F F， YANG Z J， CHEN J F， et al. An analytical analysis of the full-range behaviour of grouted rockbolts based on a tri-linear bond-slip model［J］.Construction and Building Materials，2009， 24（3）： 361-370.

［7］尤春安，战玉宝.预应力锚索锚固段的应力分布规律及分析［J］.岩石力学与工程学报，2005，24（6）： 925-928.

［8］蒋忠信.拉力型锚索锚固段剪应力分布的高斯曲线模式［J］.岩土工程学报，2001，23（6）： 696-699.

［9］张晓华，王旭，周亚龙，等.桩底复合式后注浆灌注桩的竖向承载特性研究［J］.建筑科学与工程学报，2023，40（5）：206-215.

［10］赵春风，刘鹏伟，赵程，等.黏性土中桩侧后注浆单桩抗压承载性能室内模型试验研究［J］.土木与环境工程学报（中英文），2024，46（4）：23-28.

［11］张乐文，刘传波.新型锚杆及岩土锚固新技术［J］.公路交通科技，2004，21（7）：26-29.

［12］石明生，夏威夷，王复明，等.高聚物锚固体与粉土间黏结性能试验研究［J］.岩土工程学报，2020， 41（10）：724-730.

［13］李秀钦.基于PLAXIS的地铁深基坑变形与支护结构优化研究［D］.大连：大连交通大学，2023.

［14］刘红军，于雅琼，王秀海.土岩组合地层旋喷桩止水桩锚支护基坑变形与受力数值分析［J］.岩土工程学报，2012，34（S1）：297-302.

［15］田利勇，于文华，卢育芳.Plaxis在板桩结构分析中的应用［J］.水运工程，2015（4）：194-200.

［16］朱彦鹏，陶钧，杨校辉，等.框架预应力锚托板结构加固高填方边坡设计与数值分析［J］.岩土力学，2020，41（2）：612-623.

［17］SCHANZ T， VERMEER P A， BONNIER P G. The Hardening Soil model： formulation and verification［C］// Beyond 2000 in Computational Geotechnics—10 ears of PLAXIS. Amsterdam 1999： 281-296.

［18］BRINKGREVE R B J， BROERE W. Plaxis Material Models Manual［M］. Delft， 2006.