硅片表面线痕测试方法的研究与实现

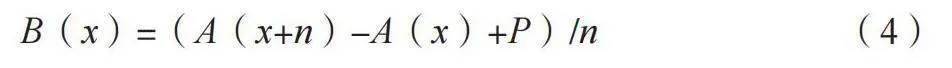
摘 要：通过搭建测试系统，‌对硅片线痕进行测试，‌分别采用移动平均法和高斯分布平均法进行处理，‌对比分析2种方法的效果。‌试验结果显示，与移动平均法相比，‌高斯分布平均法噪声消除以及平滑能力提高，具有明显优势。‌高斯分布平均法更适合用于硅片线痕测试，其能有效提高测试结果的准确性和平滑性。‌该研究为硅片线痕测试提供了一种更优的方法选择，‌有助于提高测试效率和准确性，‌对硅片制造和质量控制具有重要意义。

关键词：移动平均法；高斯分布平均法；线痕

中图分类号：TN 305 文献标志码：A

目前，光伏能源行业硅片切割的主要设备为多线切割机，多线切割机切割硅片的厚度与切割线的直径及布线间距有关，常规切割成厚度为180μm的硅片。但是因为切割线的磨损程度、砂浆颗粒大小、砂浆黏度、切割线的张力等原因，切割后的硅片存在厚度不均、翘曲、线痕等影响硅片质量的问题[1]。线痕是影响硅片质量的一个非常重要的因素，线痕会影响制绒过程的腐蚀的各向异性，从而对绒面造成影响，进而导致电池片效率降低，线痕还会增加印刷时表面的栅线虚印或者断栅等情况，同时会导致印刷时传送系统的卡片、碎片的上升。还可能导致碎片和电力衰减，‌进而影响电池片的制造和转换效率‌。当有线痕的电池片做成组件时，层压容易碎片，制成组件后，存在色差等问题，因此通过线痕检测对切割完的硅片进行挑选，可以避免后续工艺存在问题，在光伏行业原料紧张的情况下，‌减少线痕意味降低研磨损失和成本‌[2-3]。

1 系统设计

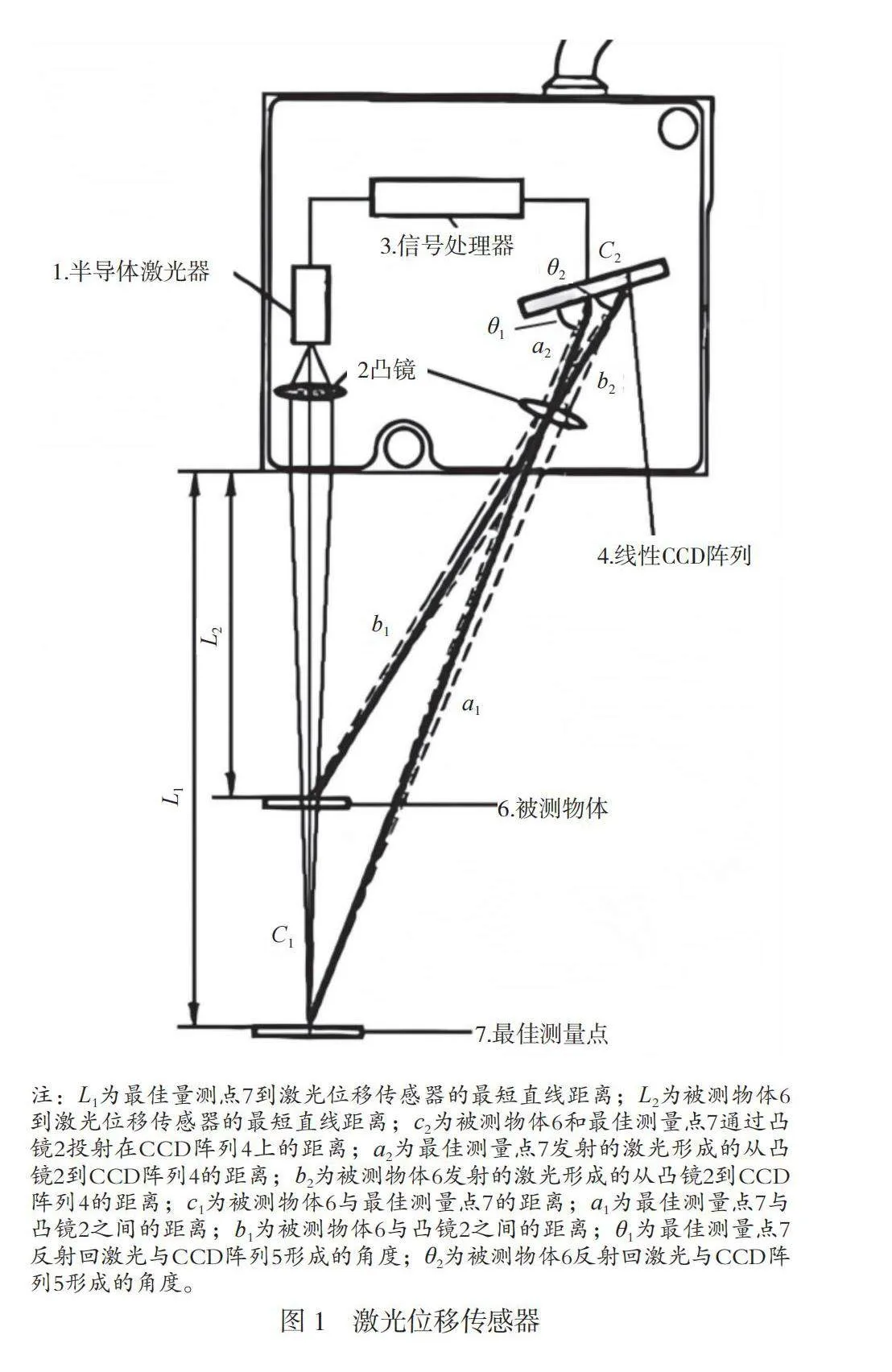
激光位移传感器的工作原理如图1所示，激光位移传感器由半导体激光器1通过凸镜2发射一束稳定、‌高精度、‌单色、‌相干的激光束，‌该激光束照射到被测物体6表面。‌被测物体6表面反射部分激光，‌这些反射光通过凸镜2被线性CCD阵列4接收，经过信号处理器3计算被测物体的位移量。同样的原理通过最佳测量点7反射光的路径和相位差异，‌传感器计算被测物体的位移量，‌并将结果实时显示、‌存储和查看。‌最佳量程点7是凸镜2的焦点位置，它发射到线性CCD阵列4上所形成的角度为θ1，被测物体6发射到线性CCD阵列4上所形成的角度为θ2。激光位移传感器设计线性CCD阵列4的安装角，使a1、b1以及c1所形成的三角形与a2、b2以及c2所形成的三角形为相似三角形。其中，L1、a1、a2以及θ1为已知值，C2和θ2可以经过信号处理器采集到。

其中，c1、L2分别如公式（1）、公式（2）所示。

（1）

L2=L1-c1 （2）

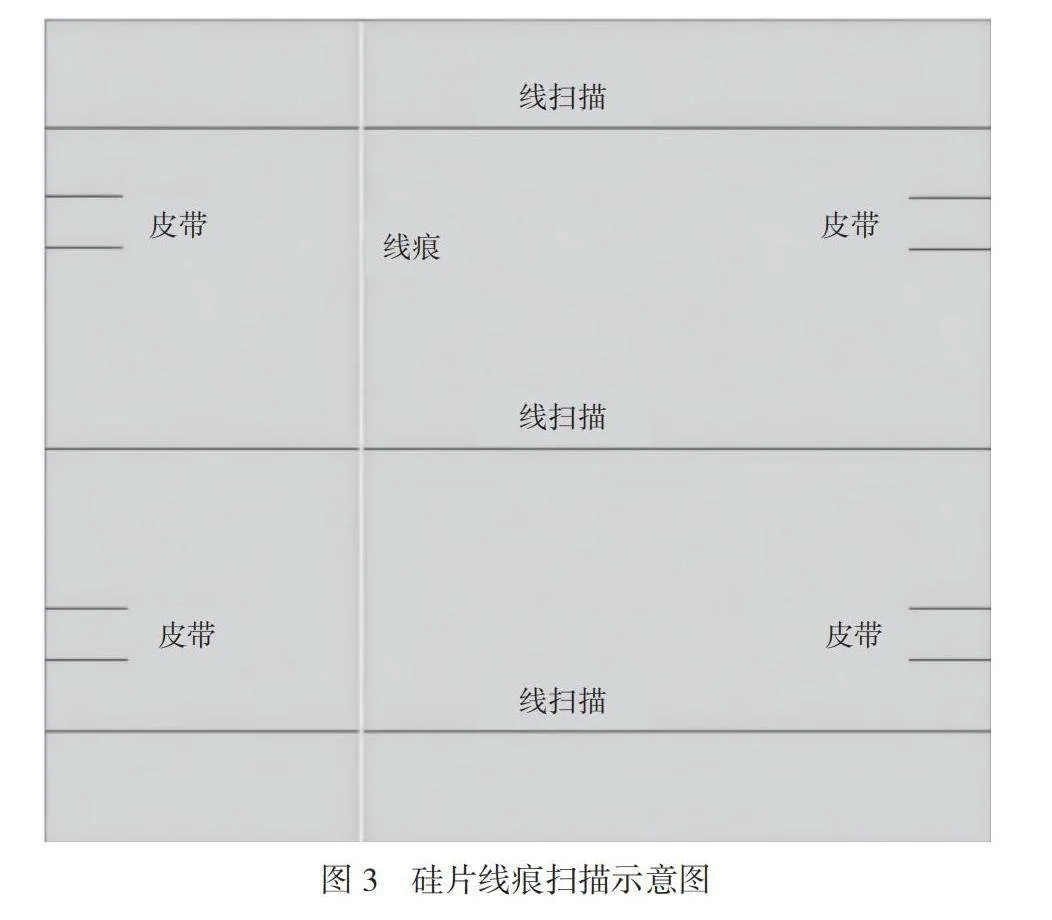
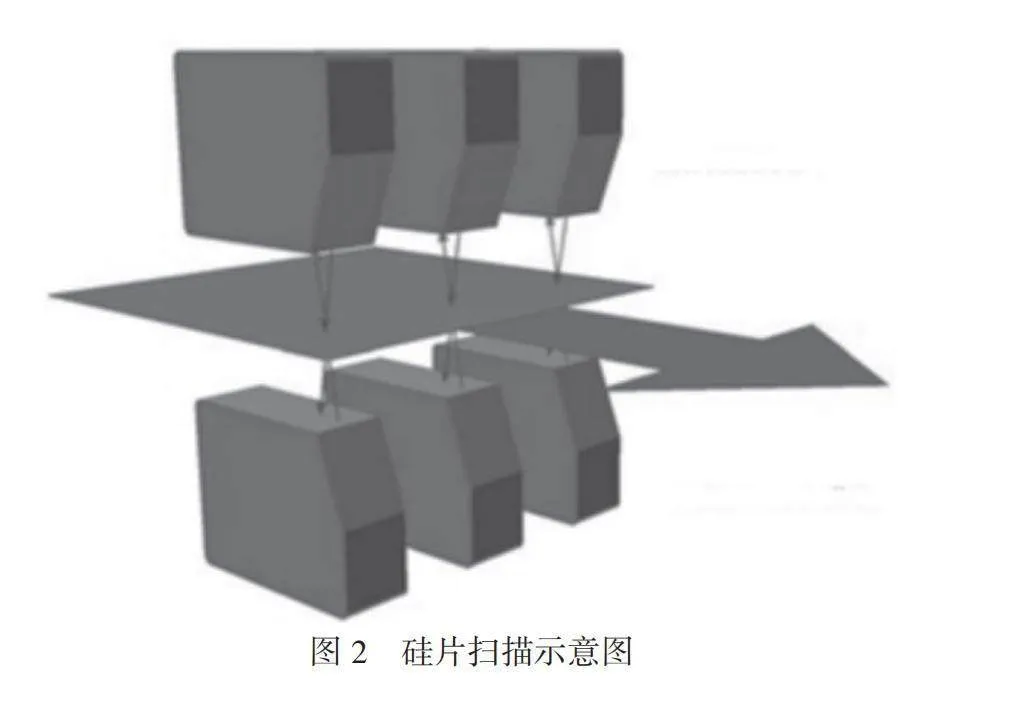
如图2和图3所示，硅片在传输皮带上进行移动，通过6个激光三角传感器线扫描正、反2个面，每个面扫描左中右3条线，采集6条线的数据（公式（1）中），然后对数据进行光滑处理，生成表面轮廓（要求硅片线痕方向与运动方向垂直）。取最大值作为线痕值。本次研究在运行速度为250mm/s的前提下进行，采用158的硅片进行试验样，样本硅片厚度为180μm～200μm，硅片从花篮中自动流到皮带进行传送。

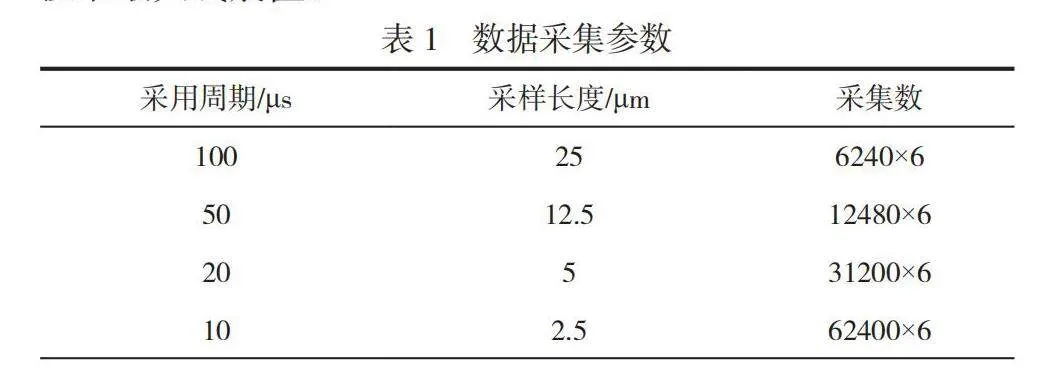
数据采用周期与硅片表面采样长度的关系见表1。根据数据统计显示，存在的线痕宽度一般大于27.5μm而采用周期为25μm时，与线痕宽度接近，属于临界值，容易漏掉线痕值。当采用周期小于50μm时，采集数据过于庞大，系统容易出现因数据处理速度过慢而导致漏检的情况。因此本文研究的对象采取每50μm采用1个点的采用周期。

采集的数据可以生成硅片的轮廓，但是需要计算硅片的线痕，本文介绍一种使用高斯分布函数进行光滑处理，使数据成光滑平整的没有线痕的在基准线上的值，再使用原始数据一一对应地减去光滑处理后的数据，生成线痕轮廓，再分段取最大线痕值。

2 线痕计算过程

本文研究的线痕计算方法有2种，即移动平均法、高斯分布平均法。

2.1 移动平均法

移动平均法是一种常用的数据降噪处理方法，‌它通过计算数据的移动平均值来平滑数据并降低噪声的影响。‌该方法使用一个滑动窗口，‌在窗口内取数据的平均值作为当前数据点的估计值。如图4所示，移动平均法的每次样本范围为2mm，结合表1的数据采集参数设置，2mm的距离对应158个采样点。采用移动平均法进行平滑处理，如公式（3）所示，将x的前n-1个厚度求和，然后将当前点往后移n的厚度与当前点厚度的差值与之前的和相加，取平均值，如公式（4）所示（n=158，x=[1-（12480-158）]）。如公式（5）所示，使用原始数据减去平滑处理后的数据，得到线痕数据。如公式（6）所示，根据需要将线痕数据分段，然后取最大值作为当前段的最大线痕值，最后在最大线痕值中取最大值作为线痕结果。

P=∑xlt;zlt;x+nA（z） （3）

式中：A为原始的厚度值；P为n长度范围内的求和。

B（x）=（A（x+n）-A（x）+P）/n （4）

式中：B为当前点与n点的厚度的差值进行移动平滑值。

y（x）=A（x）-B（x） （5）

式中：y为x的线痕值。

（6）

式中：max是求数组的最大值的函数；c为最终的线痕值。

2.2 高斯分布平均法

高斯函数也称为正态分布，因其平滑且逐渐衰减至0的特性而被广泛应用于降噪和模糊处理。基于高斯分布来计算权值，‌对信号进行加权平均，以消除噪声。‌其特点是越接近中心点的权值越大，‌越远离中心点的权值越小。采取高斯函数计算方法对数据进行平滑处理，计算过程如公式（7）所示（高斯分布函数），然后采取高斯函数计算常量Z，计算n高斯的积分，如公式（8）所示。对原始的数据进行积分后取平均（如公式（9）所示），积分中只取整数进行计算，积分计算中A（x）的x的权重为1，前后n/2的值的权重都小于当前x的权重，从而保证最大不失真。公式（5）中A（x）是采集原始数据，将n个数的线痕值按照高斯分布后进行离散积分，然后除以Z值，以取均值，生成滤掉线痕后的数据。如公式（6）所示，根据需要将线痕数据分段，然后取最大值作为当前段的最大线痕值，最后在最大线痕值中取最大值作为线痕结果。

g（x）=c‧ex2/b （7）

（8）

（9）

式中：B为当前点与前后n/2点的厚度的差值进行移动平滑值。

3 测试过程

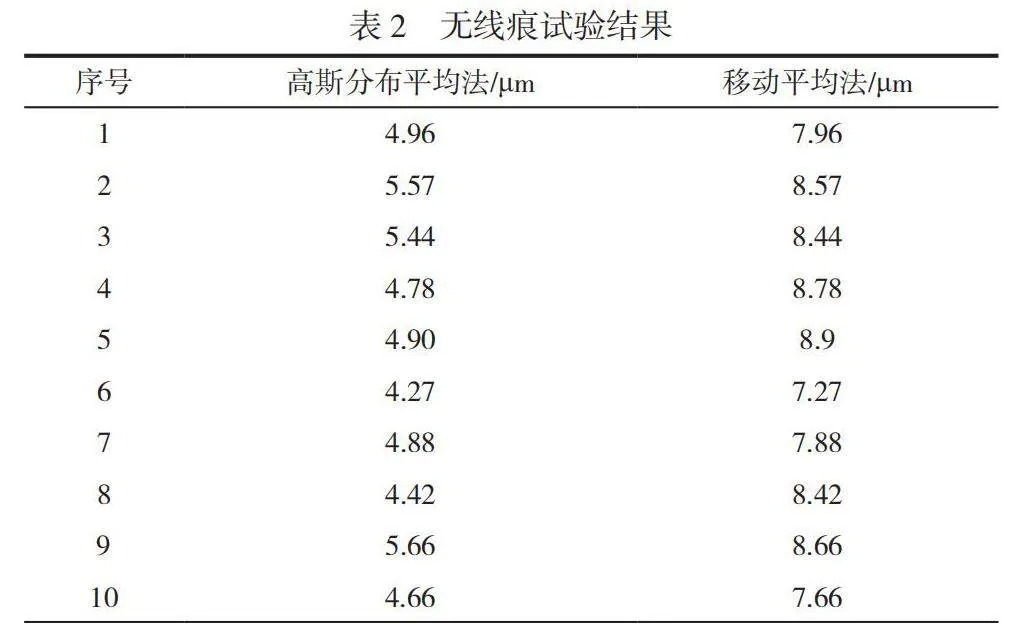
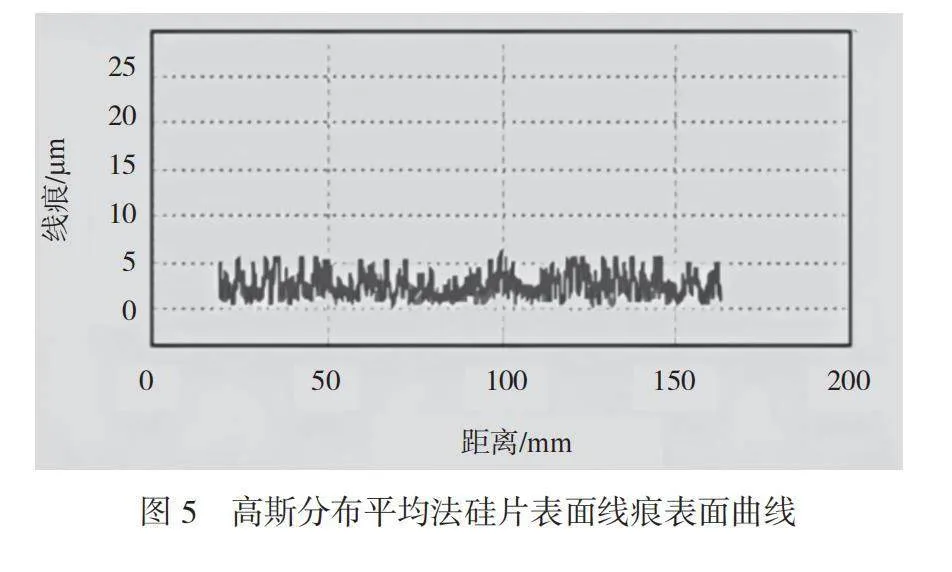
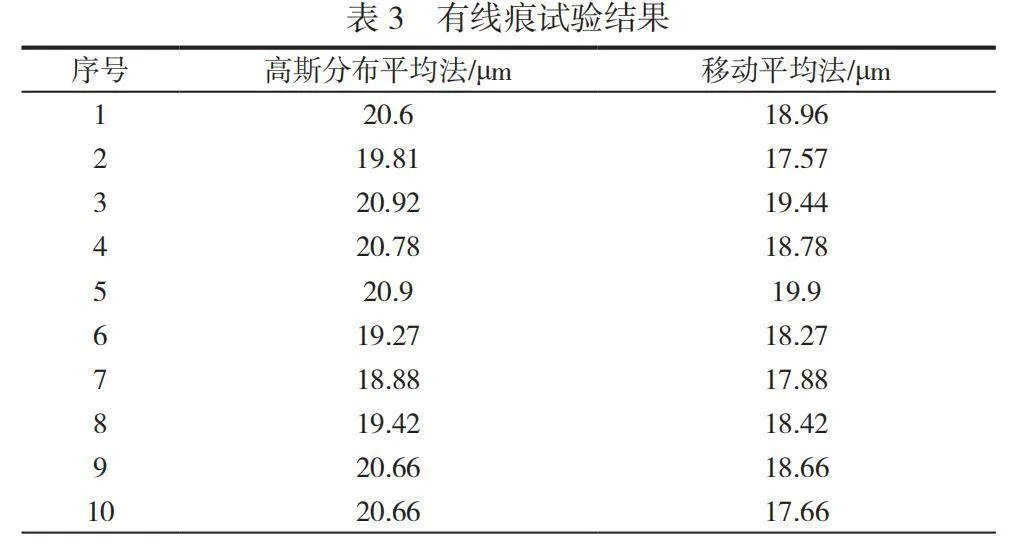
准备1片无线痕的硅片和有线痕的硅片。分别在软件中设置高斯分布平均法和移动平均法各测试10次，共计40次，数据记录见表2和表3，硅片表面轮廓如图5、图6所示。

由表2和图5可知，对应的是同一组探头上、下表面的线扫表面轮廓曲线图，其中深色表示上表面的线扫描轮廓图，浅色表示下表面的线扫描轮廓图。将同一个没有线痕的硅片在移动平均法和高斯分布平均法下分别测试10次，测试结果见表2，试验表明在高斯分布法测试线痕值的结果小于移动平均法。由表2可知，高斯分布平均法的平均值为4.954μm，均方差约等于0.3076，而移动平均法平均值为8.154μm，均方差约等于0.3517。无线痕的硅片测量值越小，产生误判的概率越低。高斯分布平均法的消噪能力比移动平均法高。

选取1片有线痕的硅片，使用粗糙仪测试线痕值为21.2μm。经过高斯分布法和移动平均法分别测试10次，测试结果见表3。高斯分布平均法的平均值为20.15μm，均方差约等于0.6195，而移动平均法平均值为18.55μm，均方差约等于0.7157，数据表明高斯分布法计算的平均值20.15μm与粗糙仪测试线痕值21.2μm更接近，偏差为4.9%，移动平均法与粗糙仪测试线痕值的偏差为12.5%。对平均值的偏差、均方差值进行比较，高斯分布法平滑能力和噪声处理能力比移动平均法高。由于移动平均法使用相同的权重，‌它可能在平滑数据的同时，‌也保留了较多的噪声或不必要的细节。‌高斯分布法通过权重分配，‌能够更有效地平滑数据，‌同时保留重要的特征。‌高斯函数的形状使它在平滑数据时更自然和流畅，‌通过对比试验验证了这一理论。

4 结语

本文对2种线痕测试方法进行研究，其核心是使用移动平均法和高斯分布平均法对原始数据进行平滑处理，然后计算线痕值。基于高斯分布来计算权值，‌对信号进行加权平均，以消除噪声。‌其特点是越接近中心点的权值越大，‌越远离中心点的权值越小，‌从而能够在去除噪声的同时，‌更好地保留信号的主要特征。移动平均法虽然简单易懂，‌计算速度快，也能去除噪声，‌但它在处理过程中可能会平滑掉图像的细节，‌导致图像质量下降。测试试验证明，高斯分布平均法消除噪声的能力、平滑能力都比移动平均法高。

参考文献

[1]郑博文，周波.一种非接触式硅片厚度及翘曲度自动检测系统.计量与测试技术，2016（6）：43-45.

[2]高茜，张占，任军海.浅析多品硅片线痕对电池的影响[J].轻工标准与质量，2013（2）：25-26.

[3]郑晓峰 ，郑博文 ，蒋立正.硅片总厚度偏差及翘曲度检测装置研制与测试 [J].仪表技术与传感器，2017（11）：113-115.