基于结构检测的既有建筑安全性分析

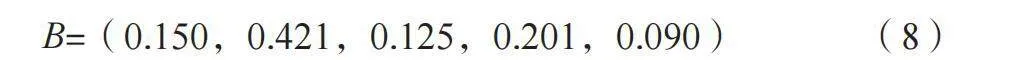
摘 要：本文结合实际工程，在对既有建筑结构安全性鉴定检测的基础上，引入数学模型，建立既有建筑安全性分析模型，并对研究背景进行深入分析。首先，根据相关规范和工程实践经验建立既有建筑安全性分级方法并给出了采用该方法分级后各级相应的加固建立方案。其次，基于层次分析法和模糊综合评价方法建立既有建筑安全性评价模型，重点论述该计算模型核心思路。最后，对研究背景中的既有建筑结构安全性进行分析，分析结果表明，该建筑处于二级，可继续使用，但应对局部构件进行补强。本文研究内容对合理利用老旧建筑物、延长建筑使用寿命具有现实意义。

关键词：既有建筑；安全性分析；模糊综合评价；混凝土强度；碳化深度

中图分类号：TU 746；TU 93" 文献标志码：A

20世纪80年代我国建筑行业发展迅速，建设了大量的民用、工业建筑，存在建筑标准较低、建筑施工技术相对落后、建设年代久远、建筑材料老化、腐蚀等问题，使大多年代久远的既有建筑存在不同程度的损伤[1-2]。如果继续使用，就可能会影响人民群众生命财产安全，而拆除重建又会对居民正常生活、资源环境以及生态环境等产生不利影响[3]。因此如何科学、合理修缮现状老旧建筑、尽量恢复其正常使用功能延长其使用寿命是现阶段建筑行业一个重要的研究方向[4]。在前人的研究中，针对既有建筑多采用强度、耐久性以及外观等方式分别对建筑钢筋混凝土结构安全性进行分析，各参数自成系统，缺乏整体性评价理念。基于此，本文引入数学模型建立既有建筑整体性评价模型，对既有建筑安全性进行评价。

1 研究背景及结构检测结果

1.1 研究背景

某地下商场始建于20世纪90年代，结构类型为框架结构，该建筑物主要作为地下商城使用至今，该建筑设防烈度为7度，结构安全性等级为1级。该建筑物为地下一层钢筋混凝土楼盖结构，局部为框架结构，采光采用钢网架结构，该商场有9处出入口，建设时主要将其作为地下人防设施，后因时代发展以及经营需求更改为地下商城。该工程由钢筋混凝土建设而成，因此其安全性分析主要是针对钢筋混凝土现状条件进行检测和分析，为确保建筑物使用安全，对该建筑钢筋混凝土工程外观、强度以及耐久性等进行检测。

1.2 外观检查

由于建设年代久远，经现场查看，未发现该建筑工程钢筋混凝土结构发生明显的变形、倾斜等现象，墙体结构也未发现明显酥松，不存在因地基不均匀沉降而导致钢筋混凝土结构裂缝的现象，基本确定该商城不存在严重静载缺陷，但使用年代较长，混凝土结构存在不同程度的损伤，主要损伤情况如下。1）柱23/D、33/J、33/A等存在受压贯穿裂缝、混凝土结构出现开裂、钢筋锈蚀。2）柱12E、36G等位置发现竖向受压裂缝和混凝土开裂。3）柱28/F在使用过程中出现局部破损、钢筋外露。4）板12-16/C-E、1-3/D-E底部存在露筋、裂缝等。5）变形缝存在漏水现象。6）梁4-6/A、14/G侧面存在裂缝。7）梁26-28/D存在破损、钢筋外露。

1.3 结构强度抽检

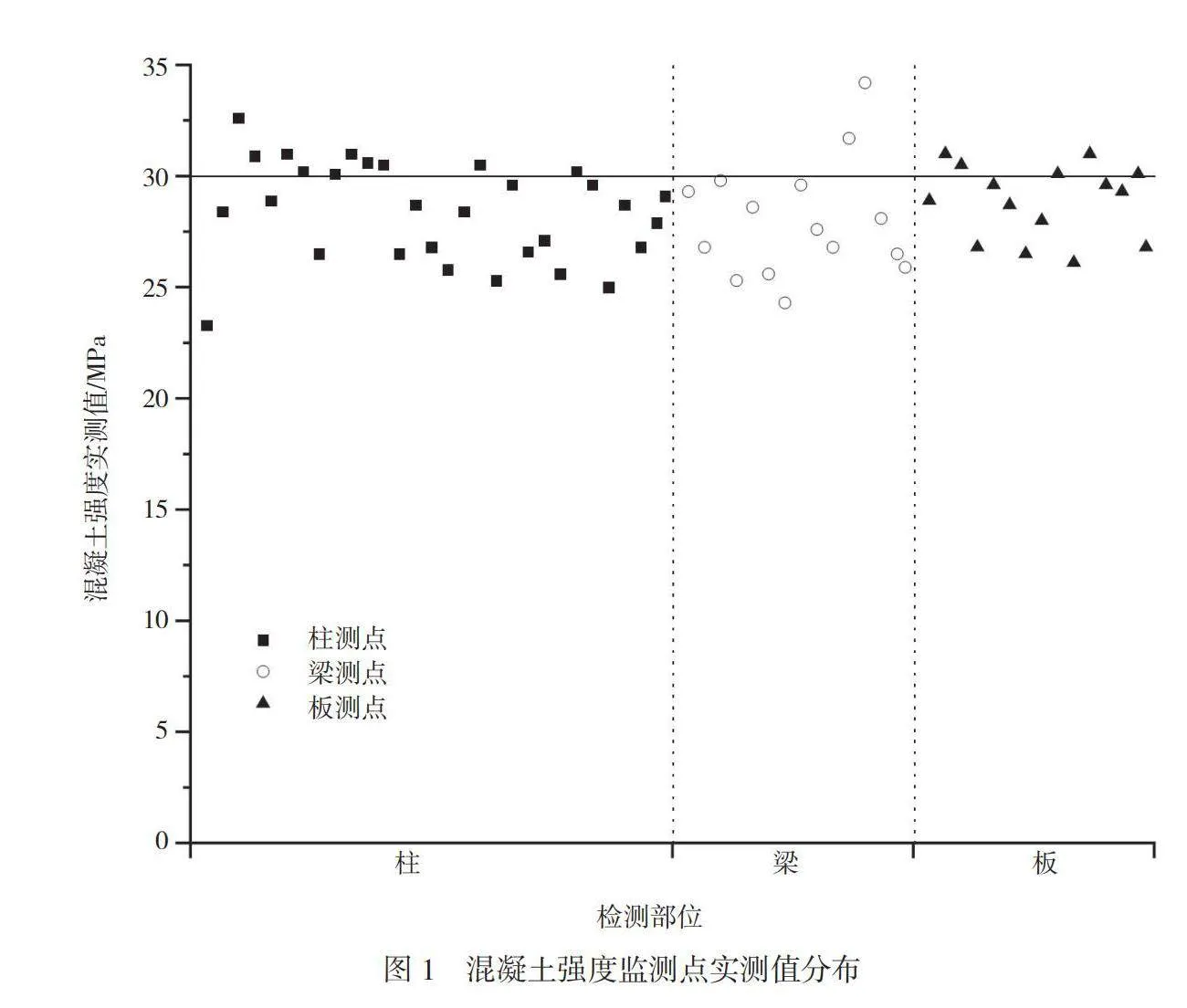
检测过程中采用取芯室内试验和现场回弹法对现状钢筋混凝土强度进行综合评定，部分评定结果见表1，所有测点所得修正后混凝土强度值分布如图1所示。本工程中钢筋混凝土强度检测多集中在30MPa左右，大部分测点实际强度大于24MPa，仅有一处修正后强度值为23.3MPa（小于24MPa），结合混凝土外观检测结果可知，在钢筋混凝土结构强度方面，本工程并未存在明显缺陷和问题。

1.4 耐久性检测

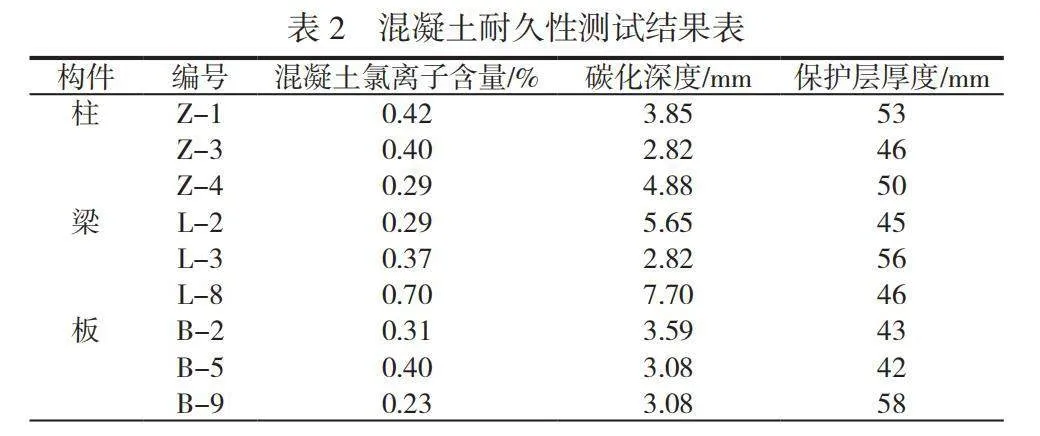
本工程针对梁板柱不同位置进行耐久性测试，部分成果见表2。在3种构件中，氯离子含量均小于0.7%，且大部分集中在0.4%以下。同时，比较保护层厚度与碳化深度的测试值可知，总体碳化深度较低。

2 建筑安全性评价结果

2.1 单一因素评估

对既有建筑的钢筋混凝土结构进行安全性评价的过程存在大量的不确定性因素，无法准确、定量地对建筑钢筋混凝土结构安全性进行评定，而模糊数学作为一门研究和处理具有模糊性现象的数学方法，能够精准地对模糊先行进行数学描述[5-6]。因此，本研究引入模糊数学理论，对建筑钢筋混凝土结构单一安全鉴定结果进行评定并形成矩阵，以便对建筑钢筋混凝土结构进行综合评定。

针对影响建筑钢筋混凝土的单一耐久性指标，首先应确定耐久性评价等级，本研究根据相关规范要求并结合工程实际，建立钢筋混凝土构件安全性等级分级，见表3。

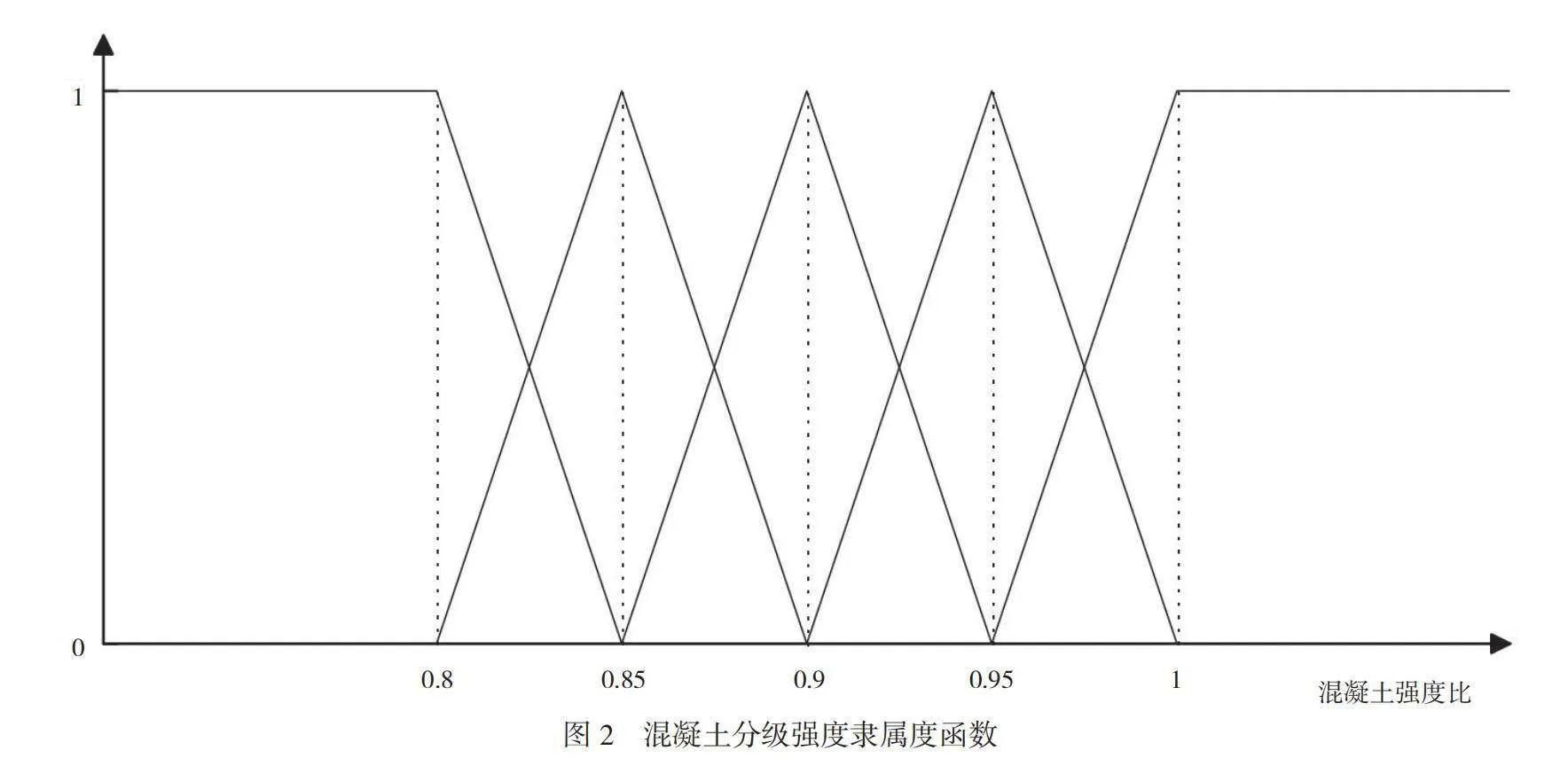
其次，根据不同指标检测值与结构安全性之间的关系，采用分级隶属度函数，确定评价矩阵，以混凝土强度为例，将混凝土强度检测值f1与混凝土强度设计值f2的比值P作为评价指标，并根据混凝土强度比数值结合混凝土强度分级隶属度函数（如图2所示）建立单一因素评估结果。

根据上述隶属度函数原理，分别对检测获取的各单一因素与钢筋混凝土强度之间建立关系，见表4。并采用隶属度函数建立各因素的评估结果。

2.2 建立评价体系

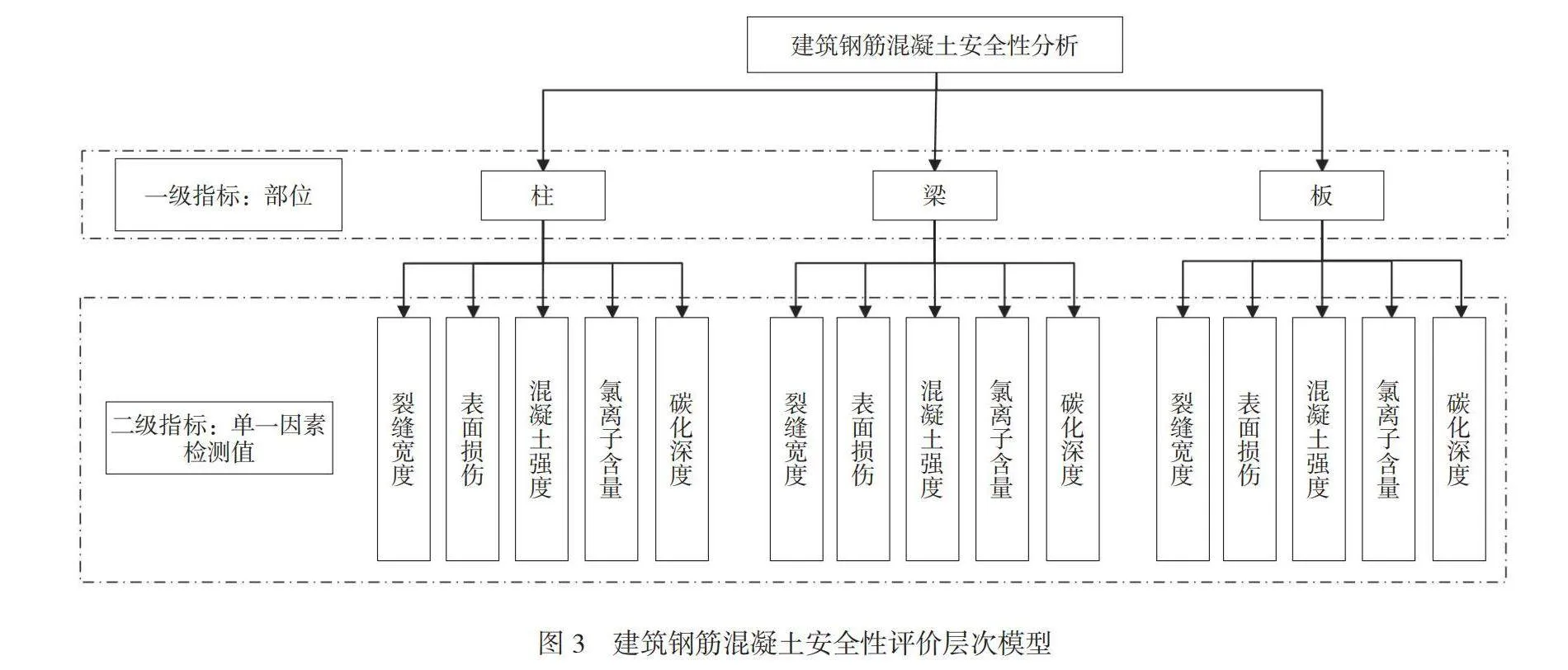
多级模糊综合评定方法是模糊关系合成原理，对多个因素对主体的隶属度等级进行综合性评价的一种方法，能够对不确定信息进行量化，并得到评价对象的评价结果。结合本研究内容建立的二级模糊综合评价层次模型如图3所示。本文建立的二级模糊综合评价模型中一级指标为钢筋混凝土结构构件的部位或属性，如此划分的原因在于不同地区、不同建筑类型、不同使用过程所造成的现状建筑混凝土结构受损情况不一致，导致不同构件之间不具备可比性。而对相同构件来说，根据结构安全性检测结果并结合上文所述单一因素评价方法建立评价矩阵，以此实现模糊问题数值化，以便后续分析。

根据上述计算原则，首先将安全性分析分为若干个不相交的子集，在本文建立的多级模糊综合评定方法中，先将安全性分析分为若干个不相交的子集，该因素集为一级指标，随后根据上述计算原则，结合上文所述单一因素评价方法，将单个因素转换为二级指标，如公式（1）所示。

U={ui1，ui2，...，uij} （1）

式中：uij为第i个因素子集中的第j个二级指标。

针对同级因素的重要性程度，可采用层次分析法，以数字标度法建立评价矩阵，并计算得到同级因素之间的重要性程度矩阵，如公式（2）所示。

A={a1，a2，...，am} （2）

式中：A为评价等级权重。

公式（2）是以权重形式表示的评价矩阵，该矩阵在建立过程中具有一定的主观性，因此需要对上述矩阵进行归一性和非负性检验，检测方法可参照层次分析法对权重矩阵的检测方法，如果所构建的评价矩阵不能够满足相关要求，就需要进一步修改直至满足要求。

随后从影响评价对象的单个因素出发，建立评价对象对因素集元素的隶属程度，如公式（3）所示。

（3）

式中：rij为因素集中第j各因素的隶属度。

将相同指标下的单个因素所建立的隶属程度建立为该指标下的模糊评价关系矩阵，如公式（4）所示。

R={rij} （4）

分别对单个因素的模糊评判结果建立集合为R，评估的计算过程如公式（5）所示。

B=A·R （5）

综上所述，矩阵B为最终的模糊综合评判结果。

2.3 研究背景安全性评价结果

根据上文所述评价方法，结合层次分析法，计算所得研究背景中建筑安全性对于一级指标的权重如公式（6）所示。

A1=（0.59，0.23，0.18）

A21=（0.35，0.23，0.14，0.12，0.16）

A22=（0.30，0.37，0.09，0.10，0.14） （6）

A23=（0.42，0.25，0.12，0.12，0.09）

以柱为例，所建立的模糊评价关系B2如公式（7）所示。

（7）

B2=（0.335，0.200，0.074，0.242，0.120）。

上述结果即为柱构件的模糊评价关系，按照上述计算方法分别计算梁、板的模糊评价关系，并将其作为R1，随后计算研究背景的模糊评价关系，如公式（8）所示。

B=（0.150，0.421，0.125，0.201，0.090） （8）

根据上述计算结果，结合最大隶属度原则，认为研究背景的建筑钢筋混凝土结构安全性等级为二级，即结构安全性较好，该建筑物可继续使用，但需要对具体病害位置进行处理。

3 结语

本文以实际工程为研究背景，在结构检测结果的基础上，系统综合地对既有建筑安全性进行分析评价，所得结论如下。1）针对建筑钢筋混凝土结构检测所得各类参数，引入数学方法，建立安全性评价模型，该模型能够将模糊问题数值化、分散参数系统化，实现了整体、系统、准确地对既有建筑安全性进行分析的功能。2）采用所研究的既有建筑安全性评价模型对研究背景进行评价，评价结果显示，该建筑物混凝土结构安全性等级为二级，须对病害位置进行修补处理。

参考文献

[1]齐尚榕，杨黎黎.既有地下人防商场建筑结构检测鉴定与加固设计研究[J].江西建材，2023（1）：78-79.

[2]廖晓星.某办公楼建筑结构检测及对应加固施工技术应用[J].广州建筑，2016，44（4）：41-44.

[3]张鑫，李安起，赵考重.建筑结构鉴定与加固改造技术的进展[J].工程力学，2011，28（1）：1-11，25.

[4]邹勇，张京街，曹淑上，等.既有办公建筑改造为医院建筑前检测与鉴定[J].重庆建筑，2019，18（5）：57-61.

[5]何炜.改变使用功能的既有建筑结构检测与鉴定实例分析[J].建材与装饰，2018（20）：48-49.

[6]许本东.既有建筑结构的检测、鉴定及加固探讨[J].四川建筑科学研究，2007（3）：86-88.