基于孪生网络的货车滚动轴承异常检测

摘 要：轴承是铁路列车走行部中的关键组成部分，其工作环境复杂，容易发生故障，不能保障列车运行安全。根据经验对运营条件下的货车故障轴承进行识别，缺乏智能检测技术。本文基于孪生网络（Siamese）和局部离群因子（Local outliers factor， LOF）算法实现了复杂轴承特征的异常检测。在真实运营条件下验证了方法的有效性。结果显示，利用傅里叶变换的频域信号识别效果比时域信号更显著；与传统方法相比，孪生网络和分类算法结合的方法对故障和正常轴承特征的分类效果更好；LOF和一类支持向量机（One Class SVM，OCSVM）作为分类器均能实现4.4%和5.6%提升，而LOF算法分类效果比OCSVM更好。

关键词：货运列车；滚动轴承；故障诊断；神经网络；振动分析

中图分类号：TP 311" " " " " " " 文献标志码：A

现阶段基于振动信号的滚动轴承故障诊断方法研究已经比较深入，其应用也取得了阶段性进展。基于信号处理的故障诊断技术比较成熟，诊断效果较好，对数据量要求不高且计算快速，其多应用于在线监测应用场景。基于数据驱动的智能诊断技术主要用于离线分析应用场景。随着传感技术发展以及历史监测数据不断积累[1]，建立智能诊断模型，与基于信号处理的故障诊断技术相比，其诊断精度更高。随着人工智能识别方法体系的快速发展，其研究成果广泛应用于滚动轴承的故障诊断[2]。目前，研究对象主要是普通轴。此外，基于数据驱动的智能诊断技术须保证数据分布相同，当对列车轴承故障进行诊断时不能充分利用实验室中的滚动轴承数据[3]。本文采用时频分析方法对在实际运行条件下的故障和正常轴承数据进行分析。在该基础上提出一种基于轴承特征相似性的异常识别算法，准确诊断铁路货车轮轴承早期故障，防止故障进一步恶化，避免过度耗损轴承服役性能。

1 异常检测模型

1.1 Siamese特征提取模型

本文建立孪生网络（Siamese）特征提取模型，基于计算原理利用一维卷积神经网络（Convolutional Neural Networks， CNN）的特征提取功能[4]。基于卷积运算提取输入数据的局部特征，输入层至隐藏层映射为一个特征提取层。考虑输入数据之间的相似性。由于轴承振动数据的故障与正常特征在不同频带中的反映比较明显，因此以数据对的形式建立初始样本集，利用正常（故障）数据建立2个初始数据对，将其转化为输入向量，分别输入2个特征提取网络，提取独立的特征向量。利用曼哈顿距离定义输入向量之间相似距离尺度L，将其作为损失函数来进行网络训练。损失函数计算过程如公式（1）所示。

L=yD2+（1-y）max（a-D2，0） （1）

式中：L为损失函数，为输入向量间相似距离尺度；D为样本特征间的欧氏距离；y为当样本匹配时的标签；a为设定的阈值。当距离超过a时，损失为0；当输入向量一和输入向量二都为正常（或异常）时损失函数更小；当输入向量一和输入向量二不均为正常（或异常）时损失函数更大。在该过程中，2个网络结构相同且参数共享。将训练后得到的特征结果以二维数组形式映射至二维平面中，即适用于轴承分类的特征。

1.2 特征分类模型

对提取后的样本特征进行特征分类和故障样本诊断。本文采用基于相似性特点的局部异常因子算法来进行分类。采用LOF算法计算每个点o与其邻域点的局部可达密度比来反映样本的异常程度。设第k距离dk以及第k可达距离rk（p，o），dk为目标点P至其第k个最近邻点的距离。

任意点p的局部可达密度如公式（2）所示。

（2）

式中：lrdk（p）为点p的第k邻域内点至p的平均可达距离的倒数；rk（p，o）为点o至点p的第k可达距离rk（p，o）=max{dk（o）d（p，o）}；rk（p，o）=max{dk（o）d（p，o）}；Nk（p）为点p的第k距离以内的所有点的集合。

任一点p的局部离群因子LOFk（p）如公式（3）所示。

（3）

式中：LOFk（p）为局部离群因子；lrdk（o）为点o的第k邻域内至o的平均可达距离的倒数；点p的邻域点Npk的局部可达密度与点p的局部可达密度之比的平均数越接近1，p的邻域点密度越接近，越可能与邻域点输入同一簇；平均数越﹥1，p的异常分数越高，其是异常点的可能性越大。

1.3 混淆矩阵

模型训练完成后，需要采用科学的评价方法对其效果进行评估。混淆矩阵是预测和评价神经网络结果的重要工具。矩阵的每一行为真实归属类别，每一列为预测类别，如公式（4）所示。

（4）

式中：TP为模型预测为正类的正样本；TN为模型预测为负类的负样本；FP为模型预测为正类的负样本；FN为模型预测为负类的正样本。公式（4）的4个指标为由混淆矩阵衍生的适用于分类算法的通用评价指标，用于量化评价模型分类效果。Precision（精准率）为在预测为正的样本集合中预测正确的样本的比例；Recall（召回率）为实际为正的样本中预测正确的样本的比例；Accuracy为预测正确的样本数占总样本的个数；F1-score为统计学中用来衡量二分类精度的指标。

2 试验设计与数据处理

2.1 试验测台设计

改造后的双轮对滚动实验平台（测试台架如图1（a）所示）可同时进行双轴测试。在测台与轴承间存在相对位移，因此采集数据为包括轴承振动和测台振动的复合数据。因此，其分析频率范围与传统意义的轴承故障范围有所差别，需要采用高频采样的方式对其特征范围进行覆盖识别。

在卡钳平台布置与轴承竖向一致的传感器，收集轮对的传递振动加速度信号。传感器类型为灵敏度为10 g的三轴50G加速度传感器。振动采集过程也是轴承的磨合过程，在该过程中红外测温探针会周期性伸缩，实时探测轴承温度。在温度稳定后，进行振动数据采集（如图1（b）所示）。车轮型号为RE2B，直径为840 mm，采样频率为10 240 Hz，转速为300 r/min，列车时速约35 km/h，试验在无负荷状态下运行。

2.2 数据处理

利用试验测台完成数据采集后对原始振动信号进行处理。本文的数据处理流程共分为以下3步。

2.2.1 数据预处理

在测试过程中，由于测温探针会周期性伸缩，导致出现周期性异常值，该值对模型训练不利，因此需要进行剔除。原始数据采样时间长，轴承振动信号具有一定的周期性，根据试验中的采样频率以及车轮转速，以2转为1个样本将原样本进行分割。例如，在试验中振动传感器采样频率f为10 240 Hz，车轮转速n为300 r/min，根据数据长度计算L如公式（5）所示。

（5）

经过计算，L=4 096，计算后可以使用移动窗口分割方法（窗口内4 096点）对原始数据进行分割。

2.2.2 数据集建立

将从实验平台收集的所有类型的数据按2∶1的比例分为训练集和测试集，这是一种常见的数据划分方法，可以保证样本训练的均衡性。

2.2.3 信号时频域转换

对原始的高频采样信号来说，其时域信号特征冗杂，区分度较低，其频域信号以特征频率的形式表示数据，区分度更高。为了比较使用时域信号和频域信号作为模型输入对分类结果的影响，利用快速傅里叶变换将重新采样的片段转换为相应的频域信号。快速傅里叶变换是对离散傅立叶变换快速求解的一种算法，计算过程如公式（6）所示。

X（u）=Xeven（u）+Xodd（u）Wu 2K " （6）

式中：X（u）为结果序列中的第u个元素，对应频域中的第u个频率分量；Xeven（u）为对输入序列偶数索引部分经过子序列计算后的第u个频率分量；Xodd（u）为对输入序列奇数索引部分经过子序列计算后的第u个频率分量；Wu 2K为旋转因子，即在变换的区间内等间隔采样序列的频谱函数。

3 实例分析

首先，本节对高频采样的轴承振动数据时频域特征进行分析。其次，对比了时频域样本输入特征提取后的效果，对提取层的有效性和准确性进行验证。最后，基于不同的分类模型验证了本文所提方法效果很好。

3.1 数据特征分析

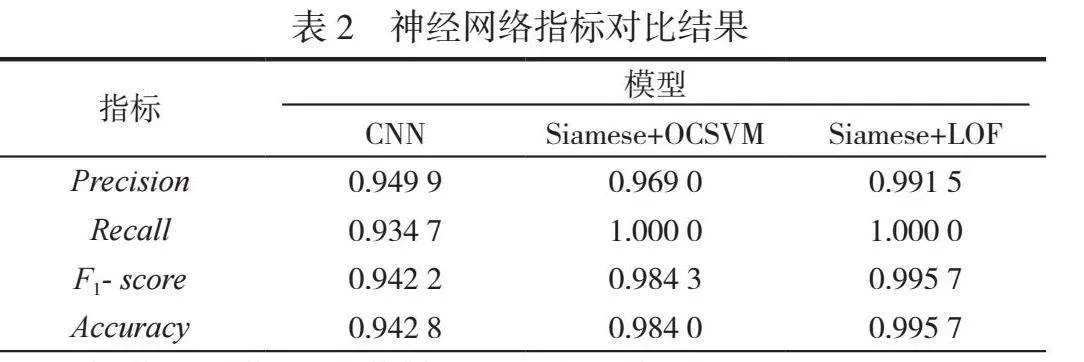
对高频采样的振动数据来说，采用传统的分析方法对其数据主要特征进行初步分析。从数据集中随机选取2个划分后的正常和故障样本，进行最值、标准差和极差等传统时域指标计算，计算结果见表1。由表1可知，对有某些故障特征的样本来说，其故障特征整体指标值大于正常样本，为区分提供了可能性。基于表2结果，使用传统数据降维方式提取其特征和主要成分进行分析，发现时域下的正常与故障数据样本之间存在一定区分度，但是其特征还存在较大重合，不利于设定区分界限。

3.2 时、频域特征提取效果对比

使用传统数据降维方式进行特征提取，难以有效区分特征。本节展示卷积神经网络对正常和故障轴承数据的特征提取效果。其中，原始时域数据集每批次样本长度为4 096，转换后的频域数据集样本长度为2 048。由于存在模糊界限，因此时域样本在识别正常样本的过程中容易误判，无法同时对正常和故障轴承进行准确预测。频域样本分类准确度较高，分类效果更显著，频域数据更能反应特征，在正常轴、故障轴分类神经网络模型中，先将时域样本转化为频域样本，再进行训练。

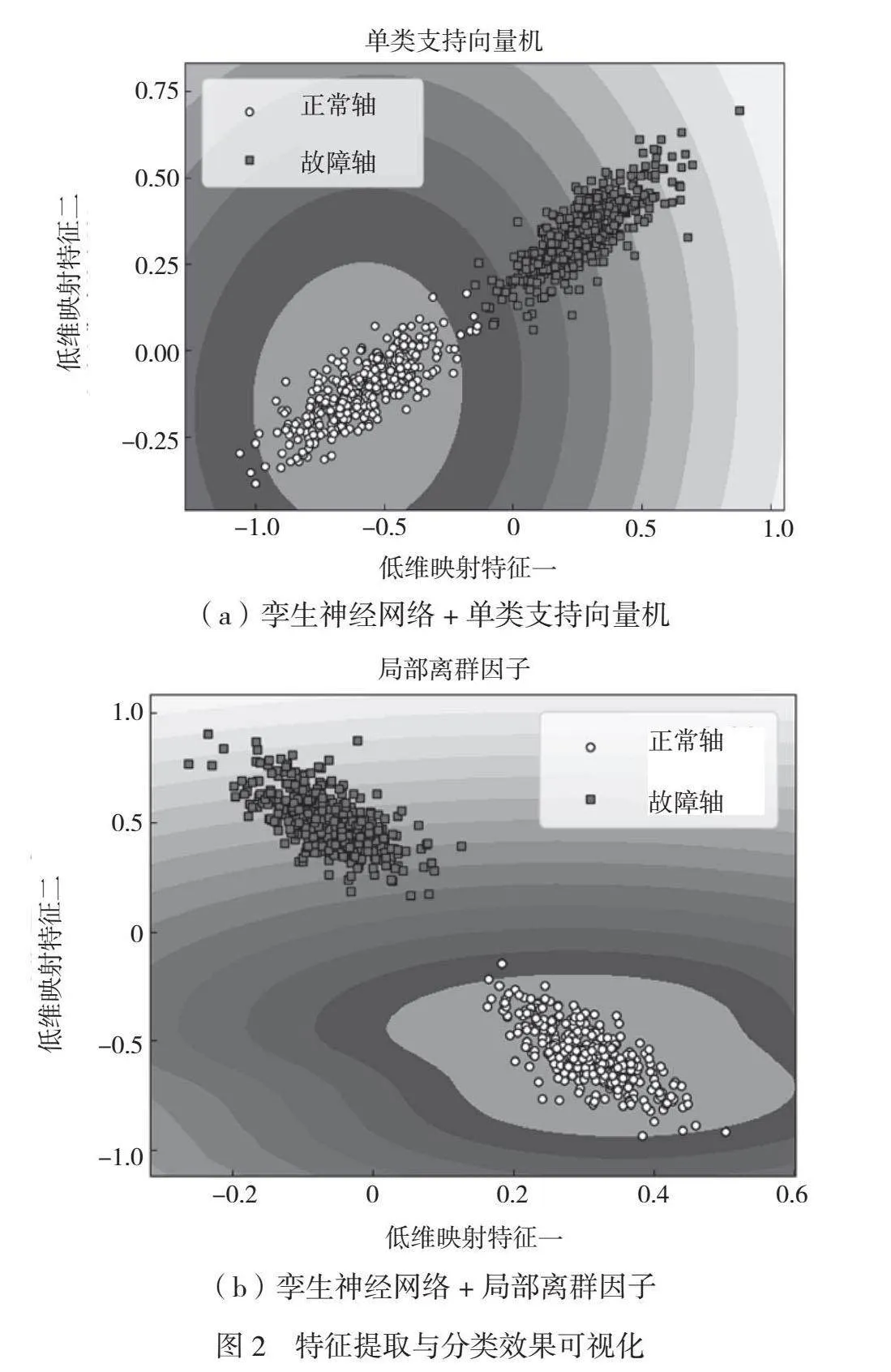
将原始时域数据以及变换后的频域数据输入Siamese进行特征提取，由于在输入和迭代过程中均对样本向量间的相似性特征进行了提取，因此其得到的分类特征在卷积分类的基础上增添了相似性信息，进一步区分了正常和故障边界。将频域数据输入Siamese进行特征提取后，再输入OCSVM和LOF分类器进行分类工作训练。得到无量纲低维映射特征。特征提取与分类效果可视化如图2所示。图2中内环区域为分类器按照提取特征收敛得到的决策边界。判定测试样本边界外为异常，边界内为正常。

从图2可以看出，Siamese提取的特征分布范围更小，样本点更密集。这说明考虑相似性特点后，提取特征间的波动性更小，收敛的边界适用性更强。虽然OCSVM分类器收敛的边界能有效涵盖大多数正常样本点，但是其边界会造成较多点的误判。LOF分类器收敛的边界更灵活，可以涵盖的数据点更多。

与传统CNN网络相比，本文模型初始损失比CNN初始损失少，收敛速度更快。使用OCSVM或者LOF分类器对Siamese进行结合，其分类效果比传统CNN好，可优先考虑。

为了量化对比模型差异，采用Precision、Recall、F1-score和Accuracy 4种指标，对3种模型的测试集分类结果进行对比，对比结果见表2。

由表2可知，与传统CNN方法相比，Siamese + OCSVM与Siamese + LOF方法的各项指标均有提高，分类效果更显著，准确度分别提升4.4%、5.6%，LOF分类器性能比OCSVM分类器更好，可优先考虑。

4 结论

本文设计了双轮对轴承实验平台，在工程条件下采集故障与正常轴承的加速度数据。在该基础上提出一种基于孪生网络和局部离群因子算法的货车滚动轴承异常检测模型。模型测试结果显示其可以有效提升识别准确度。

本文提出的数据采集和异常检测模型在一定程度上还原了真实条件下异常轴承的特征识别过程和数据采集结果，考虑相似性的特征提取和分类算法可以降低在工程条件下的数据波动造成的影响。以后将进一步提高特征提取过程的准确性，并尝试解决在工程条件下数据采集的波动性问题。

参考文献

[1]杨宇，于德介，程军圣.基于EMD与神经网络的滚动轴承故障诊断方法[J].振动与冲击，2005，24（1）：85-88.

[2]刘韬，陈进，董广明.KPCA 和耦合隐马尔科夫模型在轴承故障诊断中的应用[J].振动与冲击，2014，33（21）：85-89.

[3]肖雄，王健翔，张勇军，等.一种用于轴承故障诊断的二维卷积神经网络优化方法[J].中国电机工程学报，2019，39（15）：4558-4568.