混合候鸟优化算法求解柔性作业车间调度问题

摘 要：针对最大完工时间最小化的柔性作业车间调度问题，提出一种混合候鸟优化算法。结合轮盘赌策略生成初始种群，提高初始种群的质量。在传统候鸟优化算法的基础上对鸟类进化阶段进行改进，将共享邻域解替换为共享基因片段，避免算法陷入局部最优，设计了一种基于路径的重连的邻域结构来引导跟飞鸟进化。对进化后的个体采用随机爬山算法进行局部搜索，对关键路径上的关键工序的加工机器进行替换，扩大搜索范围，从而获得最优解。设置正交试验确定算法的重要参数组合，通过基准算例的仿真试验，使用相对百分比偏差与弗里德曼非参数配对检验来比较所提算法的有效性以及可行性。试验结果表明，在10个算例中，所提算法在多个算例上均能获得最优值，平均RPD值最小，且与其他对比算法具有显著性差异。

关键词：柔性作业车间调度；最大完工时间；候鸟优化算法；随机重启爬山算法

中图分类号：TP 165" " 文献标志码：A

作业车间调度优化一直是生产管理与组合优化等领域的热门研究话题。柔性作业车间调度问题（Flexible Job Shop Scheduling Problem， FJSP）是JSP的延伸和扩展，是一类复杂的NP-hard问题[1]。

计算机技术以及仿真技术的发展为FJSP问题的研究开辟了新的思路。智能优化算法在调度问题上得到了广泛应用。其中，候鸟优化算法[2]由于参数少、局部搜索能力强等优点，常被用于处理车间调度问题。WEI L等[3]提出了一种基于博弈论的动态多目标候鸟优化算法，将博弈论引入算法中。ZHANG B等[4]提出一种改进的离散迁鸟优化（IDMBO）算法，以解决无等待流水线车间调度问题（NWFSSP）。

随机重启爬山算法（Randomly restart the hill climbing algorithm）可以在给定步骤数后从比原始跨度差的解决方案重新开始搜索，以逃避局部最小值。结合上述研究，将随机重启爬山算法与候鸟优化算法进行结合，提出一种混合候鸟优化算法，以求解柔性作业车间调度问题。在传统MBO的基础上，对算法进行改进，引入随机重启爬山算法对进化后的个体进行局部搜索，扩大搜索范围。对标准测试案例进行仿真试验，成功证实了本文所提算法的效率和实用性。

1 问题描述与模型的建立

1.1 问题描述

FJSP可以这样描述：n个工件在m台不同机器上加工，每个工件可能需要经过一道或多道工序才能完成。因为每台机器的技术参数和型号都各不相同，所以同一个工件在不同机器上的加工时间也会有所不同。

1.2 模型建立

本文以最大完工时间最小化为优化指标，建立柔性作业车间调度模型。最大完工时间表示工件的最后一道工序完成加工所需的总时间。

FJSP的优化目标函数如公式（1）所示。

（1）

式中：j为工件序号；n为工件数目；Cj为第j个工件的完工时间。

2 混合算法设计

2.1 轮盘赌初始化

初始解的优劣对算法的收敛速度和求解质量有关键的影响。为了保证初始种群的质量以及多样性，通过更少的迭代次数得到问题的最优解，针对本文的优化目标，采用随机初始化的方式生成工序序列，针对机器分配采用考虑机器加工时间的轮盘赌初始化策略。

2.2 双层编码与最优插入解码

FJSP的编解码针对工序排序和机器分配这2个子问题展开，采用融合工序与设备的并行双链式编码。这种编码方法能确保染色体编码含有充分的基因信息，避免发生死锁。

解码是将解空间转化为问题空间。本文采用一种最优插入法[5]对后续满足条件的工序执行“优先处理”操作。在对应机器上寻找满足加工的加工间隙，将工序插入与工序的加工时间接近的间隙中。这种策略为后续工序的插入提供了更多的选择，从而有机会得到更优解。

2.3 邻域结构的设计

MBO算法是一种依赖邻域搜索的元启发式方法，单一的邻域结构容易使算法陷入局部最优，不利于种群的多样性。由于领飞鸟与跟飞鸟之间的质量存在显著差异，因此，对领飞鸟和跟飞鸟执行不同的邻域结构。领飞鸟的邻域解通过随机从基于工序编码的互换变异和基于工序编码的前插变异中选择一种来生成，以保证种群的多样性

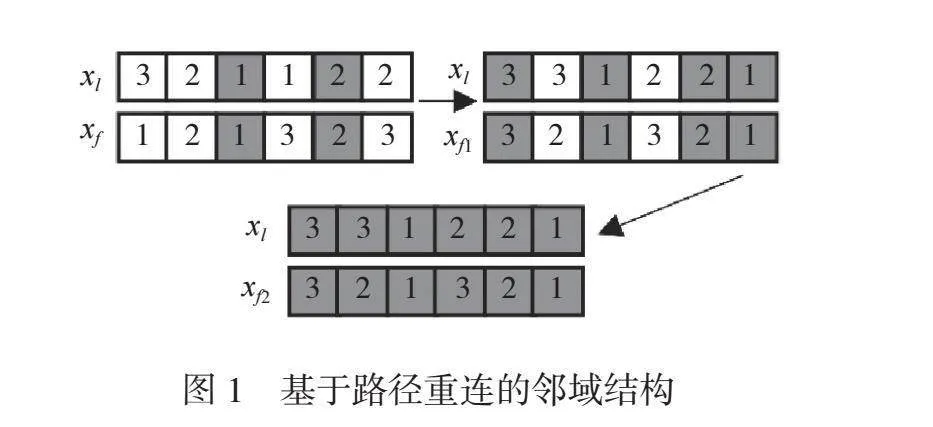
针对跟飞鸟设计一种基于路径重链接的邻域结构。通过连接领飞鸟与跟飞鸟之间的搜索空间中的假设路径来探索邻域解决方案，融合初始解和引导解之间的一些特征来找到更好的解。如图1所示，将xl跟飞鸟作为初始解，xf领飞鸟为引导解，逐渐检查跟飞鸟与领飞鸟之间的对应元素，逐渐对不同的元素进行替换，跟飞鸟慢慢向领飞鸟靠拢，在此过程中产生规定数量的邻域解xf1、xf2。

2.5 共享基因片段

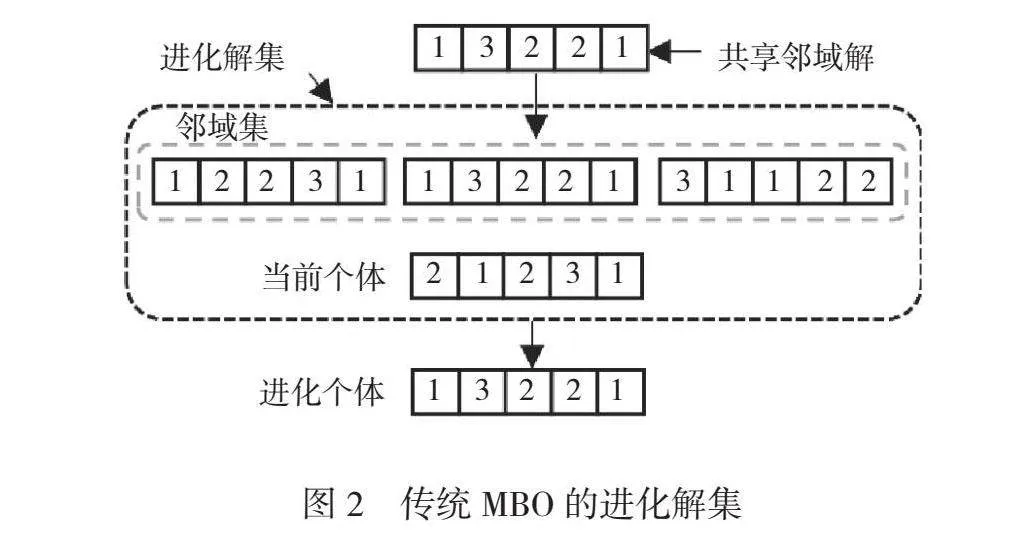
在跟飞鸟的进化阶段，鸟类通过其共享机制与其跟随鸟共享一些未使用的邻域解，如图2所示。如果后一只鸟的解决方案被前一只鸟的共享邻域解替换，那么这只鸟包括的全部信息将会完全被丢弃。这种机制使鸟群朝一个方向进化，导致种群过早收敛。

为了保留个体的优秀基因片段，提出一种改进的共享机制。如图3所示，用共享基因片段来代替共享邻域解，其中每个个体的进化解集中的非当前个体解是通过当前个体的邻域解与上一个相邻个体的邻域解进行交叉产生的，交叉后产生的个体即包括上一个个体的基因片段，又包括当前个体的基因片段，这样能够避免由个体被替换而导致优秀基因丧失的情况，保证种群的多样性。

2.8 RRHC局部搜索

为了增强种群寻优能力、扩大搜索范围在，跟飞鸟进化结束后，对种群中的个体执行局部搜索，保证种群有更大概率找到最优解。

RRHC是一种贪婪搜索算法，它可以从比原始的解决方案差的邻域解开始，重新搜索，以逃避局部最小解。因此引入RRHC对进化后的个体执行局部搜索。其中，关键路径[6]是甘特图中无空闲时间的最长路径，与调度方案的最大完工时间紧密相关。RRHC算法通过替换关键路径上的关键工序的加工机器，以尽可能地缩短最大完成时间。

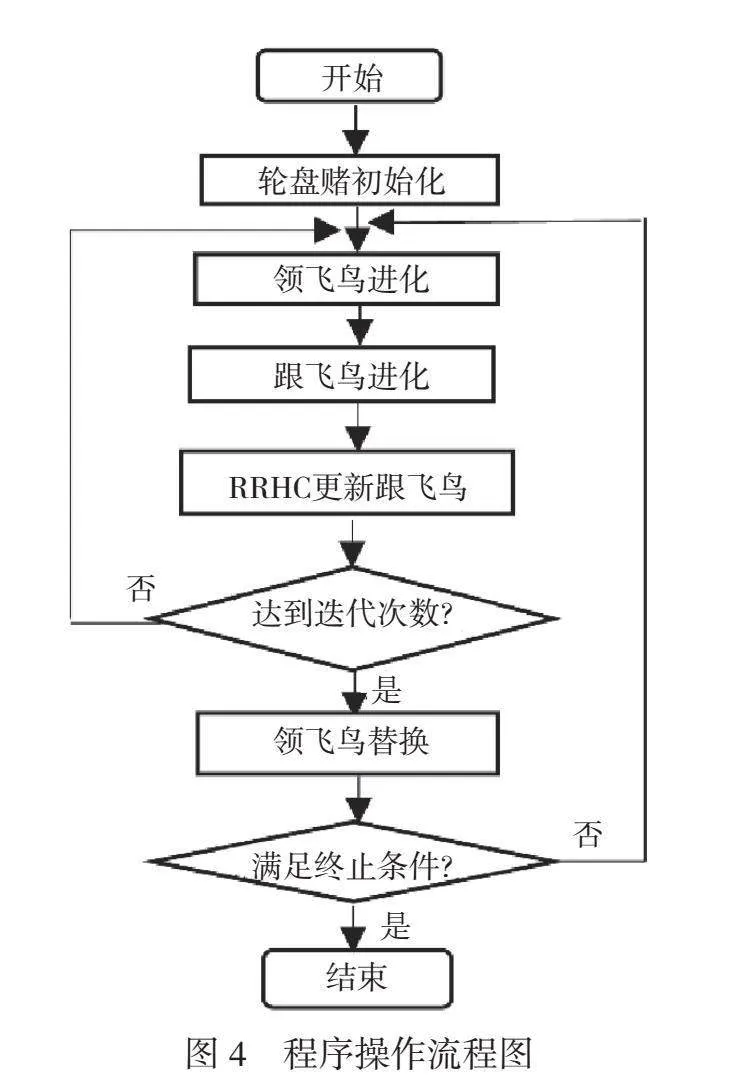
2.9 算法流程

本文算法提出的IMBO-RRHC框架流程图如图4所示。

3 仿真试验

3.1 参数设置

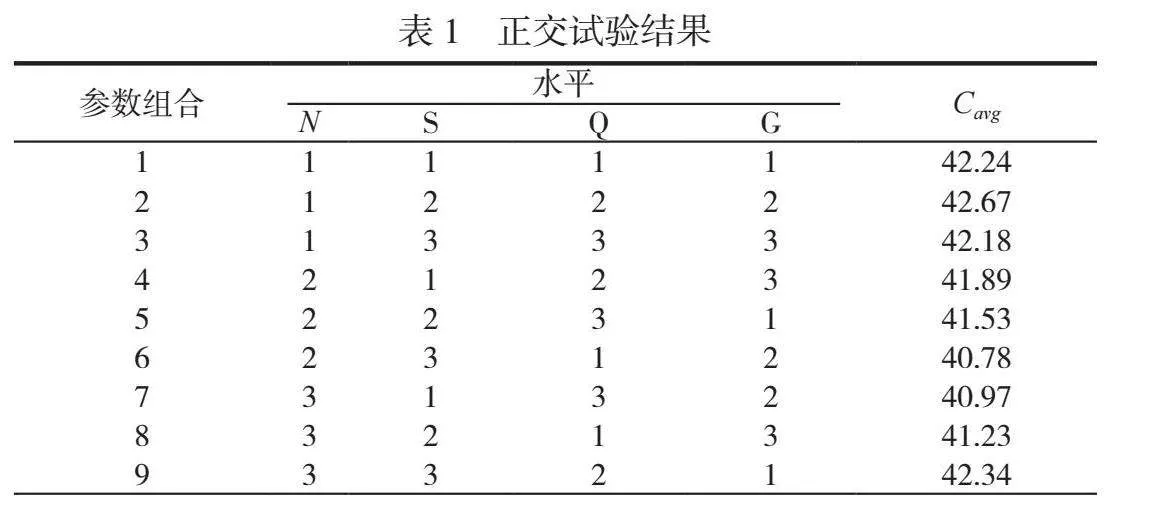
在改进算法中，RRHC的参数设置参考文献[7]，IMBO算法的主要参数如下：初始规模N（51，101，151），邻域解数量k，共享邻域解数量x，巡回次数G（3，5，10），解龄阈值limit（5，10，15），总迭代次数T （100，140，200）。其中，由于k、x这2个参数之间相互约束，不适用于正交，将k设定为3，x设定为1。针对另外2个参数，根据其参数水平，通过正交试验选出最佳的参数组合。

基于MK01算例进行试验，取目标函数的平均值作为响应变量，表1总结了所选的正交数组和相应的AVG值。由表1可知，第6组参数组合下算法能够得到更优的解决方案，因此以下试验均采用此参数设置。

3.2 改进算法可行性分析

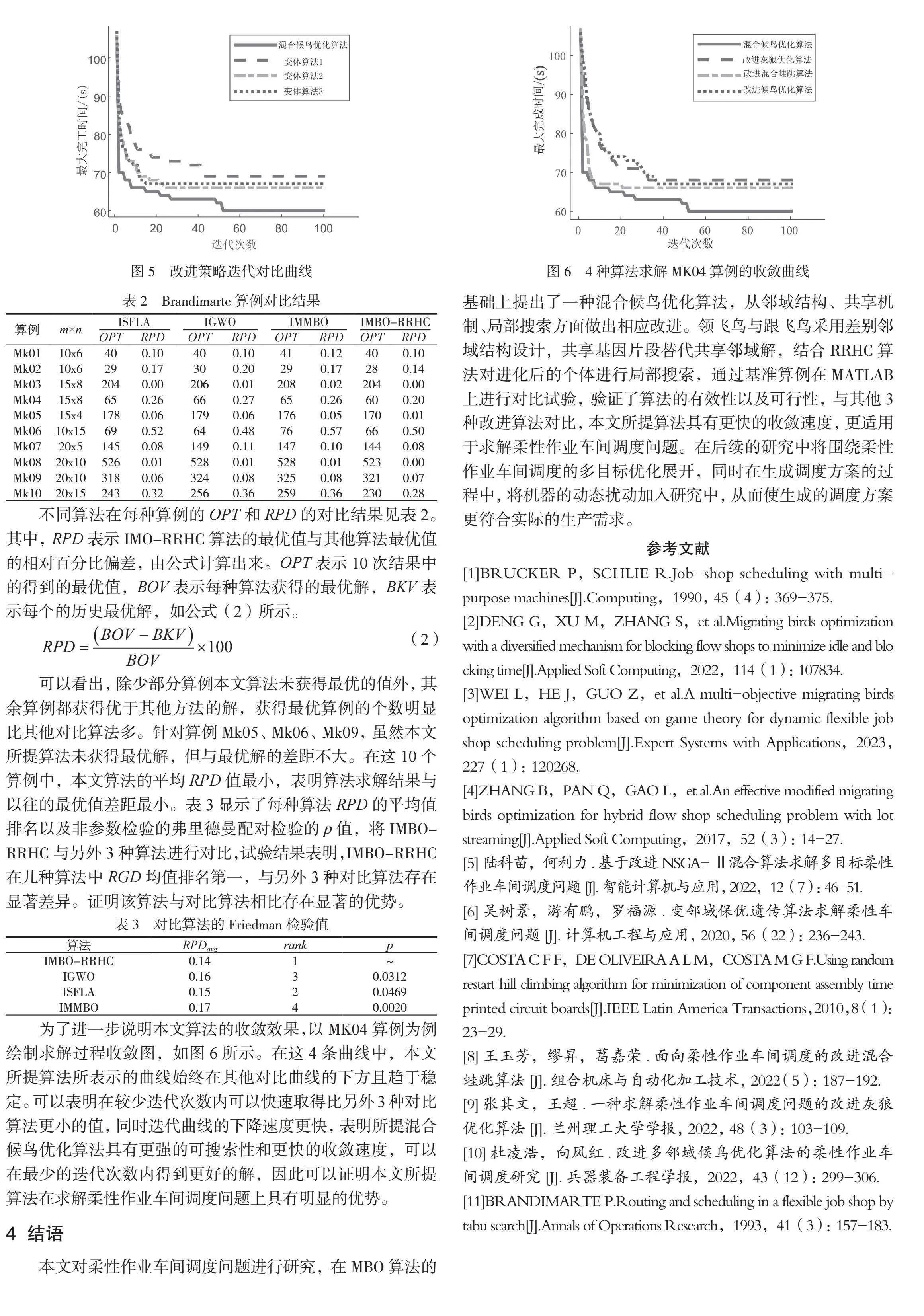
为验证改进算法的有效性，将3种主要的改进策略依次从算法中单独拿出，构造了3种不同的变体算法。在相同条件下，在MK04算例上运行本文所提算法以及这3种变体算法，得到迭代进化曲线图，如图5所示。

由图5可知，在收敛速度以及算法取得的最优值来看，IMBO-RRHC明显优于其他3种变体算法，证明了改进策略的有效性。

3.3 与元启发式算法对比

为验证本文所提算法的优越性，将本文算法与文献[8]、文献 [9]、文献 [10]所提算法进行对比（基于Brandimarte[11]算例设置试验）。

种群规模与迭代次数保持一致，采用Brandimarte的10个算例（MK01～Mk10）设置对比试验。在相同条件下，在每个算例的基础上运行10次，取相对百分比偏差（RPD）和Frideman的非参数检验进行比较。在每种情况下，获得的最优值加粗表示。

不同算法在每种算例的OPT和RPD的对比结果见表2。其中，RPD表示IMO-RRHC算法的最优值与其他算法最优值的相对百分比偏差，由公式计算出来。OPT表示10次结果中的得到的最优值，BOV表示每种算法获得的最优解，BKV表示每个的历史最优解，如公式（2）所示。

（2）

可以看出，除少部分算例本文算法未获得最优的值外，其余算例都获得优于其他方法的解，获得最优算例的个数明显比其他对比算法多。针对算例Mk05、Mk06、Mk09，虽然本文所提算法未获得最优解，但与最优解的差距不大。在这10个算例中，本文算法的平均RPD值最小，表明算法求解结果与以往的最优值差距最小。表3显示了每种算法RPD的平均值排名以及非参数检验的弗里德曼配对检验的p值，将IMBO-RRHC与另外3种算法进行对比，试验结果表明，IMBO-RRHC在几种算法中RGD均值排名第一，与另外3种对比算法存在显著差异。证明该算法与对比算法相比存在显著的优势。

为了进一步说明本文算法的收敛效果，以MK04算例为例绘制求解过程收敛图，如图6所示。在这4条曲线中，本文所提算法所表示的曲线始终在其他对比曲线的下方且趋于稳定。可以表明在较少迭代次数内可以快速取得比另外3种对比算法更小的值，同时迭代曲线的下降速度更快，表明所提混合候鸟优化算法具有更强的可搜索性和更快的收敛速度，可以在最少的迭代次数内得到更好的解，因此可以证明本文所提算法在求解柔性作业车间调度问题上具有明显的优势。

4 结语

本文对柔性作业车间调度问题进行研究，在MBO算法的基础上提出了一种混合候鸟优化算法，从邻域结构、共享机制、局部搜索方面做出相应改进。领飞鸟与跟飞鸟采用差别邻域结构设计，共享基因片段替代共享邻域解，结合RRHC算法对进化后的个体进行局部搜索，通过基准算例在MATLAB上进行对比试验，验证了算法的有效性以及可行性，与其他3种改进算法对比，本文所提算法具有更快的收敛速度，更适用于求解柔性作业车间调度问题。在后续的研究中将围绕柔性作业车间调度的多目标优化展开，同时在生成调度方案的过程中，将机器的动态扰动加入研究中，从而使生成的调度方案更符合实际的生产需求。

参考文献

[1]BRUCKER P，SCHLIE R.Job-shop scheduling with multi-purpose machines[J].Computing，1990， 45（4）： 369-375.

[2]DENG G，XU M，ZHANG S，et al.Migrating birds optimization with a diversified mechanism for blocking flow shops to minimize idle and blocking time[J].Applied Soft Computing，2022，114（1）： 107834.

[3]WEI L，HE J，GUO Z，et al.A multi-objective migrating birds optimization algorithm based on game theory for dynamic flexible job shop scheduling problem[J].Expert Systems with Applications，2023， 227（1）： 120268.

[4]ZHANG B，PAN Q，GAO L，et al.An effective modified migrating

birds optimization for hybrid flow shop scheduling problem with lot

streaming[J].Applied Soft Computing，2017，52（3）： 14-27.

[5]陆科苗，何利力.基于改进NSGA-Ⅱ混合算法求解多目标柔性作业车间调度问题[J].智能计算机与应用， 2022，12（7）： 46-51.

[6]吴树景，游有鹏，罗福源.变邻域保优遗传算法求解柔性车间调度问题[J].计算机工程与应用， 2020， 56（22）： 236-243.

[7]COSTA C F F，DE OLIVEIRA A L M，COSTA M G F.Using random

restart hill climbing algorithm for minimization of component assembly time

printed circuit boards[J].IEEE Latin America Transactions，2010，8（1）： 23-29.

[8]王玉芳，缪昇，葛嘉荣.面向柔性作业车间调度的改进混合蛙跳算法[J].组合机床与自动化加工技术， 2022 （5）： 187-192.

[9]张其文，王超.一种求解柔性作业车间调度问题的改进灰狼优化算法[J].兰州理工大学学报， 2022， 48（3）： 103-109.

[10]杜凌浩，向凤红.改进多邻域候鸟优化算法的柔性作业车间调度研究[J].兵器装备工程学报，2022，43（12）： 299-306.

[11]BRANDIMARTE P.Routing and scheduling in a flexible job shop by tabu search[J].Annals of Operations Research，1993，41（3）：157-183.