基于动态时间弯曲距离接地故障区段定位研究

摘 要：为了探究动态时间弯曲距离算法在配电网单相接地故障选线与定位中的应用方法，本文分析了该算法的实现原理。针对无分支故障线路和有分支故障线路，分别建立可量化的故障判据，通过采集零序暂态电流，计算不同区段前、后端测点的动态时间弯曲距离，并根据判据确定相应的故障区段。再利用电磁暂态仿真软件构建配电网模型，检验定位技术的实际效果。结果显示，本文建立的算法模型能够有效定位故障区段。

关键词：配电网；接地故障；区段定位技术；动态时间弯曲距离

中图分类号：TM 862" " " " " " 文献标志码：A

配电网的结构较复杂，当线路发生单相接地故障时，通常可利用电流互感器采集数据，并判断发生故障的线路区段，但是该方法的可靠性和精确性相对较低，有可能出现互感器极性反接的问题，进而影响采样精度。动态时间弯曲距离能够体现出不同测点电流波形的相似程度，为配电网线路故障区段定位提供量化依据。

1 人工接地前后零序电流特征分析

1.1 配电网接地故障模型

本文采用的配电网模型如图1所示。电压等级为10kV，L1～L3为3条线路，L1线路无故障，L3为A相接地故障线路，L2线路为L3线路的分支。在交流电路中，电容对电流的阻碍作用明显大于电阻对电流的阻碍作用，因此在配电网故障模型中仅保留线路的对地电容。将3条线路划分为5段，C01～C05为各段线路的对地等效电容。

1.2 人工接地前零序电流分析

当线路发生单相接地故障后，并假设未接入人工接地消弧装置，对于故障点的上游区段，电流从线路流向母线端；对于故障点的下游区段，电流从母线端流向线路[1]。将单相接地故障点的等效电压记为U0，该电压的表达如公式（1）所示。

（1）

式中：EA为A相电源的电动势；j为复数单位；ω为角频率；jω为线路电抗；Rd为过渡电阻的阻值；C0Σ为系统对地等效电容之和。

测点1和测点3的电流分别记为I01、I03，根据电流回路的特点，I01=-I03，相应的电流计算方法如公式（2）所示。

（2）

式中：C01为测点1对应线路的对地等效电容。

测点4的电流为I04，计算方法如公式（3）所示。

（3）

式中：C02、C03分别为测点2、3对应线路的对地等效电容。

测点2和测点5的电流的计算方法如公式（4）所示。

（4）

式中：C0i为第i个测点的对地等效电容，其中i的取值为2或者5。

1.3 人工接地后零序电流分析

在图1所示模型中接入人工接地消弧装置后，单相接地故障消失。在这一情况下，系统接地仅为变电站的金属性接地，电压源转移至母线端，因此电流从母线端流向线路。此时，将零序电压记为U'0=-EA。测点1、2、5的电流计算方法为I'0i=-jωC0iEA；测点3的电流计算方法为I'03=-jω（C02+C03+C04+C05）EA；测点4的零序电流计算方法为I'04=-jω（C04+C05）EA。

2 动态时间弯曲距离算法应用原理

动态时间弯曲（Dynamic Time Warping，DTW）是一种基于时间序列度量的算法，可用于构建最优路径，其应用原理如下：假设D和E为2个不同的时间序列，D中的元素为d1、d2、...、dm，E中的元素为e1、e2、...、en，其中m为时间序列D的长度，n为时间序列E的长度[2]。在以上2个序列中，元素可进行一一配对。DTW算法通过时间弯曲获得最优路径，降低了2个序列的总距离度量值，使其达到最小化程度。

2.1 约束条件

在寻找最优路径的过程中，需要设定约束条件，以确定边界、连续性和单调性，具体约束条件如下：最优路径的起点和终点分别为（d1，e1）、（dm，en）；规划路径时，要求其保持连续性，并且单调不减；路径可弯曲。

2.2 路径规划方法

将约束条件下得到的最优路径时间序列记为P，则有P={p1，p2，...，ps，...，pk}，k为最优路径中元素的总数量。规划路径时，任意元素ps的坐标记为（i，j），其中i为序列D中的di，j为序列E中的ej，2个元素为配对关系。选定元素ps后，其对应的下一个元素为ps+1，根据约束条件，元素ps+1仅能出现在元素ps的右侧、上方或者右上方[3]。在2个时间序列中，元素间的关系为“多对一”或者“一对多”，因此可形成不止一条路径，所有符合要求的路径记为集合Q。

规划路径时，要求2个序列的总距离最小，因此需要计算元素对间的距离。路径P中元素ps对应的距离度量值为d（ps）=（di-ej）2。最优路径的总距离计算方法如公式（5）所示。

（5）

另外，在规划路径的过程中，可通过弯曲代价累计矩阵T确定最优路径，弯曲代价为di和ej间的距离。矩阵T的数学描述方法（此处应描述为T（i，j））如公式（6）所示。

（6）

式中：参数i的取值范围为1，2，…，m；参数j的取值范围为1，2，…，n。

当i和j均为0时，矩阵T的计算结果为0。矩阵T（m，n）的计算结果即为时间序列D、E的最小距离值[4]。

3 基于动态时间弯曲距离的故障区段定位和仿真

3.1 故障区段定位方法

3.1.1 定位故障区段的判据

正常情况下，相邻测点的DTW距离计算结果较小，如果计算结果偏大，说明零序电流互感器的极性存在反接问题。采取人工接地措施前，非故障区段和故障区段的DTW距离差异明显，前者计算值较小，后者计算值较大[5]。故障定位判据的数学表示方法为DTW（D，E）Kgt;" DTW（D，E）a≠K。其中，符号“" ”表示“任意”；a为故障线路中各个区段的编号；K为故障区段。从故障判据的建立过程可知，计算DTW距离时，需要采集某区段两端的零序电流数据，但配电网靠近用户侧的线路未设置测点，无法获取故障时的零序电流，因此不能计算DTW距离。此时可设置一个动态时间弯曲距离阈值，记为Dset，当DTW（D，E）K＞Dset时，可判定为故障区段，反之则为非故障区段[6]。

3.1.2 针对故障区段的搜索方法

配电线路错综复杂，虽然故障判据能够区分正常区段和故障区段，但是当线路存在分支时，仅根据上述判据难以精确定位出发生故障的区段，因此应该建立可行的故障搜索方法。

3.1.2.1 无分支线路的故障搜索策略

无分支故障线路和有分支故障线路示意图如图2所示。图2（a）表示无分支配电网模型，f1和f2为故障点。对故障点f1来说，其上、下游的测点分别为D1和D2，接入人工接地前、后，D1测点的电流幅值变化显著，而D2测点的电流幅值变化较小，因此根据D1、D2计算的DTW距离较大。对故障点f2来说，测点D1、D2均在其上游，暂态零序电流在人工接地装置动作前、后的幅值高度接近，并且流向相同，计算出的动态时间弯曲距离较小。可见，在无分支的情况下，可逐一计算各个线路区段的DTW距离，并比较阈值Dset，当某个区段的DTW距离大于阈值时，则定位出故障区段[7]。

3.1.2.2 有分支线路的故障搜索策略

图2（b）表示有分支配电网模型，f3、f4为故障点。对故障点f3来说，测点D3测得的电流为本线路电容电流+非故障线路电容电流，而测点D4、D5的电流均为本线路电容电流，因此测点D3的电流幅值明显大于测点D4和测点D5的电流幅值。则有DTW3-4gt;Dset和DTW3-5gt;Dset。对故障点f4来说，人工接地动作前、后，流经测点D3、D4的电流为本线路电容电流和非故障线路的馈线电容电流，因此D3和D4的电流差异较小。通过测点D5的电流仅为故障区段下游的电容电流，D3、D4的电流与D5的电流差异显著，此时有Dsetlt;DTW3-5，同时Dsetgt;DTW3-4，据此可判断故障点的位置。

3.1.3 故障区段定位的通用流程

上文讨论了2种线路模型下的故障区段定位方法，当使用DTW算法进行故障线路定位时，通用流程如下所示。1）利用同步相量测量装置检测故障馈线的数据，并且将数据上传至系统主站。当线路发生单相接地故障后，采集1/4个工频周期的暂态零序电流。在人工接地动作后，再检测1/4个工频周期的暂态零序电流[8]。2）采集人工接地动作后测点的暂态零序电流数据，并计算出配电网不同区段的DTW距离，判断零序电流互感器是否存在反接，如果存在，应校正其极性。3）当配电网出现故障接地后，采集相邻测点的零序电流数据。当线路不存在分支时，从首端开始依次计算DTW距离，当满足DTWKgt;Dset时，说明区段K为出现故障的线路；当配电线路存在分支时，假设测点u在主干线路上，测点v和w在分支线路上，如果同时满足Dsetlt;DTWu-w、Dsetgt;DTWu-v，故障就出现在测点v所在的分支线路上；如果同时满足Dsetgt;DTWu-w、Dsetlt;DTWu-v，故障就出现在测点w所在的分支线路上。

3.2 故障区段定位方法仿真分析

3.2.1 仿真模型构建

本文利用PSCAD（一种电磁暂态仿真软件）构建配电网模型，系统中设计有电源G、主变压器T、馈线L1～L4，配电网模型的设计参数见表1。仿真模型的有功功率、无功功率分别为0.38MW、0.285Mvar，功率因素的取值为0.8。在线路L1上设置D1～D4共4个测点；在线路L2上设置D5～D8共4个测点；在线路L3上设置D9～D12共4个测点；在线路L4上设置D13和D14共2个测点。

3.2.2 故障定位分析

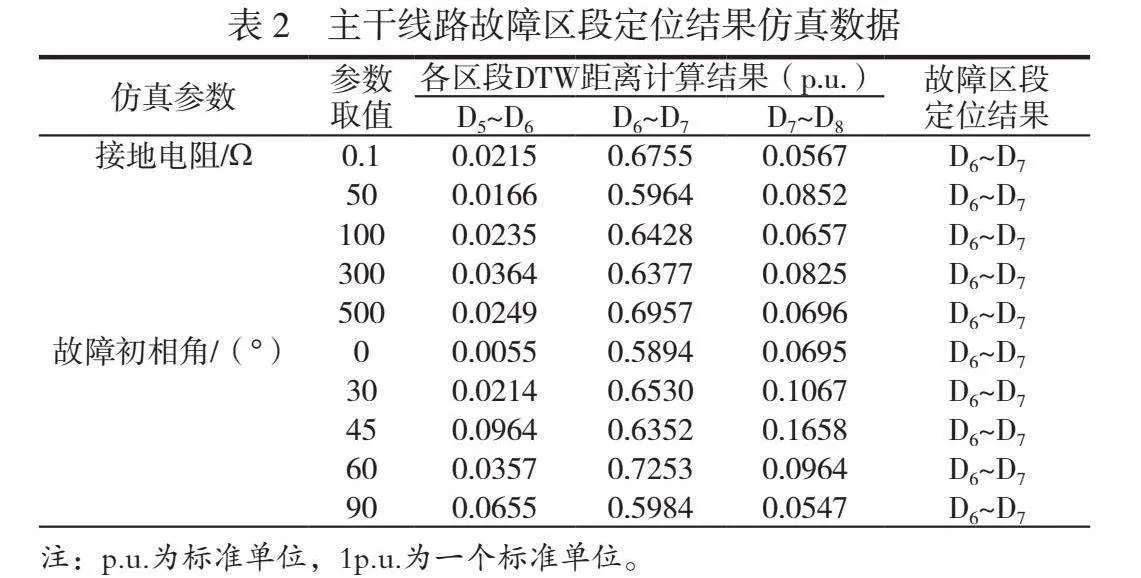
3.2.2.1 主干线路故障定位

线路L2上设置有4个测点，可形成4个区段，分别为D5～D6、D6～D7、D7～D8以及D8～末端。在仿真模拟开始后0.1s，单相接地故障点f1在区段D6～D7，又经过25ms，人工接地装置动作。零序电流数据按照10kHz的频率进行采样。在仿真软件中编写DTW算法，根据上文建立的故障搜索策略定位发生故障的区段。设置不同的故障初相角和接地电阻，定位结果见表2。

3.2.2.2 分支线路故障定位

在仿真模型中，L3为1条主干线路，L4为L3的分支线路。f2为分支线路上的单相接地故障点，位于测点D13和D14间。将不同的接地电阻和故障初相角作为仿真条件，利用软件工具计算出DTW距离，同时根据定位流程和策略明确故障区段，相应的结果见表3。

3.3 研究结果

根据以上研究过程可得以下3个结论。1）动态时间弯曲距离算法可用于计算线路上不同测点零序电流间的DTW距离，并比较不同区段的DTW距离结果，以确定可能的故障区段。无分支线路和有分支线路的故障区段判据有所不同。2）表2显示，在无分支线路故障定位模拟中，D6～D7区段的DTW计算结果明显高于其他区段，根据判据，单相接地故障发生在D6～D7。软件仿真结果与设定故障点一致，证明无分支线路故障判断方法可行。3）表3展示了有分支线路故障定位模拟结果，分支线路接入点在D10和D11间，首个零序暂态电流测点为D13。D10和D11间的DTW距离大于D10和D13间，并且Dsetlt;D10～D11、Dsetgt;D10～D13，因此故障发生在D13测点所在分支。该方法能准确定位有分支线路的故障区段。

4 结语

在配电网单相接地故障区段定位中，通过在线路上布置测点检测暂态电流，并运用动态时间弯曲距离算法计算相邻测点电流DTW距离。本文针对无分支和有分支线路，建立不同故障判据。使用PSCAD软件构建仿真模型验证算法和流程。结果显示，算法能准确定位无分支和有分支线路上的单相接地故障区段。

参考文献

[1]李卫国，许文文，王旭光，等.基于DTW距离搜索的配电网故障区段定位方法[J].电力系统及其自动化学报，2020，32（6）：80-87.

[2]庄胜斌，缪希仁，江灏，等.基于改进欧氏-动态时间弯曲距离的谐振接地配电网单相高阻接地故障选线方法[J].电网技术，2020，44（1）：273-281.

[3]艾青伟.配电网自动化系统中的小电流接地故障区段定位方法设计与实现[J].电子技术，2023，52（12）：118-120.

[4]吴泽文，伊国强，匡扶正.小电阻接地系统单相接地故障的处理与区段定位[J].电力学报，2023，38（1）：28-37.

[5]陈新岗，刘新宇，马志鹏，等.基于近似熵的小电流接地系统故障区段定位[J].计算机仿真，2023，40（1）：112-117，409.

[6]廖芳群，李海锋，陈嘉权，等.小电阻接地系统高灵敏性接地故障区段定位方法[J].电力系统保护与控制，2021，49（21）：150-158.

[7]刘红文，曾祥君，柴晨超，等.配电网柔性接地装置注入非工频小信号的接地故障检测与区段定位方法[J].南方电网技术，2022，16（6）：44-53.

[8]夏旺.配网自动化系统中接地故障区段定位方法研究[J].技术与市场，2022，29（1）：96-97.