基于优化动态窗口算法的智能机器人路径规划设计

摘 要：针对普通动态窗口算法进行动态避障后规划路径长度增加、在复杂环境中无法进行规划的问题，本文研究一种优化智能机器人路径规划算法。本文采取设置动态函数、调整运动机制和规定运动航向等策略，保证算法可规划最短路径；利用轨迹评价函数构建最佳路径的目标函数，提升机器人的避障性能，安全到达终点。使用蜂鸟云验证，结果表明，与传统哈里斯鹰算法相比，本文算法在复杂环境中规划路径更短，路径质量更佳，运动时间更少，证明算法在路径规划中适用性较好。

关键词：优化动态窗口算法；智能机器人；路径规划；传统哈里斯鹰算法

中图分类号：TP 242" " " " " " " " " " 文献标志码：A

路径规划的目的是使机器人利用行进准则搜索最佳的无碰撞路径，根据环境掌握程度，机器人路径规划可分为全局规划与局部规划。全局规划是了解环境后求解静态环境中的最短路径，局部规划一般用于解决动态环境中的避障问题[1]。路径规划算法包括普通算法与优化算法，普通算法须提前载入信息，优化算法在既定环境中全局性较好。对路径规划优化算法研究较多，杨帆等[2]引入距离信息，在优化函数后得到最优路径；黄勇强等[3]提出融合优化A*算法和动态窗口算法的路径规划算法，完成了全局修正；常新中等[4]将动态权重引入混合金豺优化算法，增强全局探索能力。

虽然上述研究提升了算法效率，但是存在依赖参数设定、在复杂地形中无法规划等问题。优化动态窗口算法具有参数少、寻优速度快等优势，因此选取该算法进行路径规划。在静态全局规划的基础上进行实时动态规划，使算法能够有效应用于动态环境中，提升智能机器人规划路径的顺滑度。

1 普通动态窗口算法

当应用于路径规划时，动态窗口算法起到有效避障的作用。在计算过程中，机器人速度约束条件如公式（1）所示。

（1）

式中：xt为机器人处于t时刻的线速度；yt为机器人处于t时刻的角速度；ymax为角速度最大值；xt+1为机器人处于t+1时刻的线速度；yt+1为机器人处于t+1时刻的角速度；mxmax为线加速度最大值；mymax为角加速度最大值；λt为时间步长。对速度空间进行采样，获得速度集合，在该过程中生成预测轨迹，使用评估函数评分后发现最佳运动轨迹与相应速度集合。评估函数g如公式（2）所示。

（2）

式中：x为机器人的线速度；y为机器人的角速度；k1、k2和k3为评估函数权重；r为归一化过程；difference函数用于计算预测轨迹终端方位角与目标方位角的差值，差值越大，函数值越小；minimum函数用于计算预测轨迹所有坐标到障碍物的最佳距离，其评估预测轨迹与障碍物的距离，函数值越大，距离越远；speed函数用于评估线速度与角速度，线速度越大，评分越高，角速度越慢。

如果需要算法全局搜索能力更强，则可增加k1数值；如果需要机器人避障能力更强，则可增加k2数值；如果需要机器人运动更顺滑，则可增加k3数值。在实践中，算法有2个需要调整的问题。1）避障后规划路径长度偶尔会增加。2）当靠近障碍物时，k2数值增加，搜索性能显著降低。如果降低k2数值，就会触碰障碍物，还会出现无法规划路径的问题。因此，本文提出优化动态窗口算法解决上述问题。

2 优化动态窗口算法

2.1 设置动态函数

在了解全局信息的情况下，优化动态窗口算法计算静态最佳路径，在沿该路径运动的过程中，机器人不断扫描环境，当发现动态障碍物时会主动避障，调整路径。可能出现规划路径距离最佳路径较远的问题，为了使路径更短，可在优化过程中添加dynamic动态函数，将其评估函数权重标记为k4。动态函数能够使算法更快发现最短路径，优化后的评估函数g如公式（3）、公式（4）所示。

（3）

式中：dynamic（x，y）为动态函数。

（4）

式中：l1、l2、l3、l4和l5为预估轨迹中5个均分点至坐标（a，b）

的最佳距离；ω为这5个点至最佳距离的平均加权数。当ω为最小值时，预估路径最接近最佳距离，算法会优先选择该路径，因此算法规划的路径更接近最佳距离。

2.2 调整运动机制

当规避障碍物时，算法需要有较强的搜索能力和避障能力，当进行规划时，普通动态窗口算法易出现权重系数不变的问题。如果动态障碍物速度较快，就会导致避障迟滞。因此，引入动态调整机制，当机器人靠近障碍物时，动态调整数值k2开始增加，避障能力显著提升。计算机器人位置与障碍物的最佳距离，如公式（5）～公式（7）所示。

（5）

（6）

（7）

式中：wdo为机器人与障碍物之间的距离；（a1，b1）为机器人此时的坐标；（a2，b2）为障碍物此时的坐标；wdl为起点与终点之间的距离；（a3，b3）为起点坐标；（a4，b4）为终点坐标；xt为机器人处于t时刻的线速度；yt为机器人处于t时刻的角速度。k2数值与角速度成正比，与wdo成反比，距障碍物越近，k2数值越大，避障能力越好。

2.3 设定动态航向

在运动过程中，如果机器人与目标栅格存在角度差，则可能会绕行，因此本文提出以起点与首个目标点的连线水平夹角来设定动态航向。为避免错误选择子目标点导致角度差，应在筛选周围节点后根据距离设置评估函数。设（a3，b3）为起点坐标，（a5，b5）为无障碍物可行节点坐标，（a6，b6）为目标节点坐标。如果起点附近没有障碍物，那么均为可通过区域，h为下一个可通过节点，根据可通过节点距离来计算函数u的具体数值，如公式（8）所示。

（8）

式中：n1为可通过节点距目标节点与当前节点之和的最佳路径；n2为可通过节点距目标节点与当前节点之和的最长路径。h越接近目标点，函数u越大；h越接近终点，函数u越小。算法优化后机器人会直接移动至下一个可通过节点，来避免路径冗余。

3 算法路径规划过程

在既定环境中，优化动态窗口算法负责全局规划，提取关键点作为局部目标点，当出现新增障碍物时进行局部规划，保证全局路径最佳。算法路径规划过程包括以下5个步骤。1）采用栅格法在蜂鸟云创建模拟地图，对各个栅格进行编号，区分障碍物栅格与自由栅格，设置机器人的运动起止点。2）初始化处理算法参数，设时间步长λt、动态因子β、最大迭代次数Nmax、最大线速度xmax、最大角速度ymax、最大线加速度axmax和最大角加速度aymax等。3）令最大迭代次数Nmax=200，开始迭代，如果迭代次数达到最多，就可得到全局最佳路径。4）提取局部子目标点，使用算法完成采样，使用线速度与角速度（x，y）预测运动轨迹，根据结果选出最佳组合规划局部路径。5）判定局部子目标点，如果是全局目标点，则说明已到达终点，在输出最佳路径后结束运算。

4 仿真试验与分析

为验证算法有效性，采用不同算法进行仿真试验。仿真平台选用蜂鸟云，操作系统为Windows 11。采用栅格法对环境进行建模，将优化动态窗口算法与传统哈里斯鹰算法进行比较，再将优化动态窗口算法放置在新增障碍物的模拟环境中进行试验。

4.1 环境建模

采用栅格法构建节点能够精确表现墙体、路面以及障碍物的位置，虽然存在部分倾斜与重影，但是不会对后续规划产生影响。将机器人处理为小质点来忽略体积，降低误差。栅格地图环境大小为20 m×20 m，白色区域为自由区域，黑色栅格为障碍物，相邻栅格距离为1 m。坐标（0，0）为原点，从左上至右下依次计数，坐标（1，19）为起点，坐标（19，1）为终点。

4.2 设置参数

传统哈里斯鹰算法参数设置如下。粒子总数为50，动态因子β1=β2=2，最大迭代次数Nmax=200；优化动态窗口算法的参数设置如下。线加速度最大值axmax=0.2 m/s2，角加速度最大值aymax=20 rad/s，膨胀半径Robstacle=0.2 m，评价函数权重系数分别为γ1=0.05，γ2=0.2，γ3=0.2，根据参数观察轨迹。

4.3 静态路径规划试验

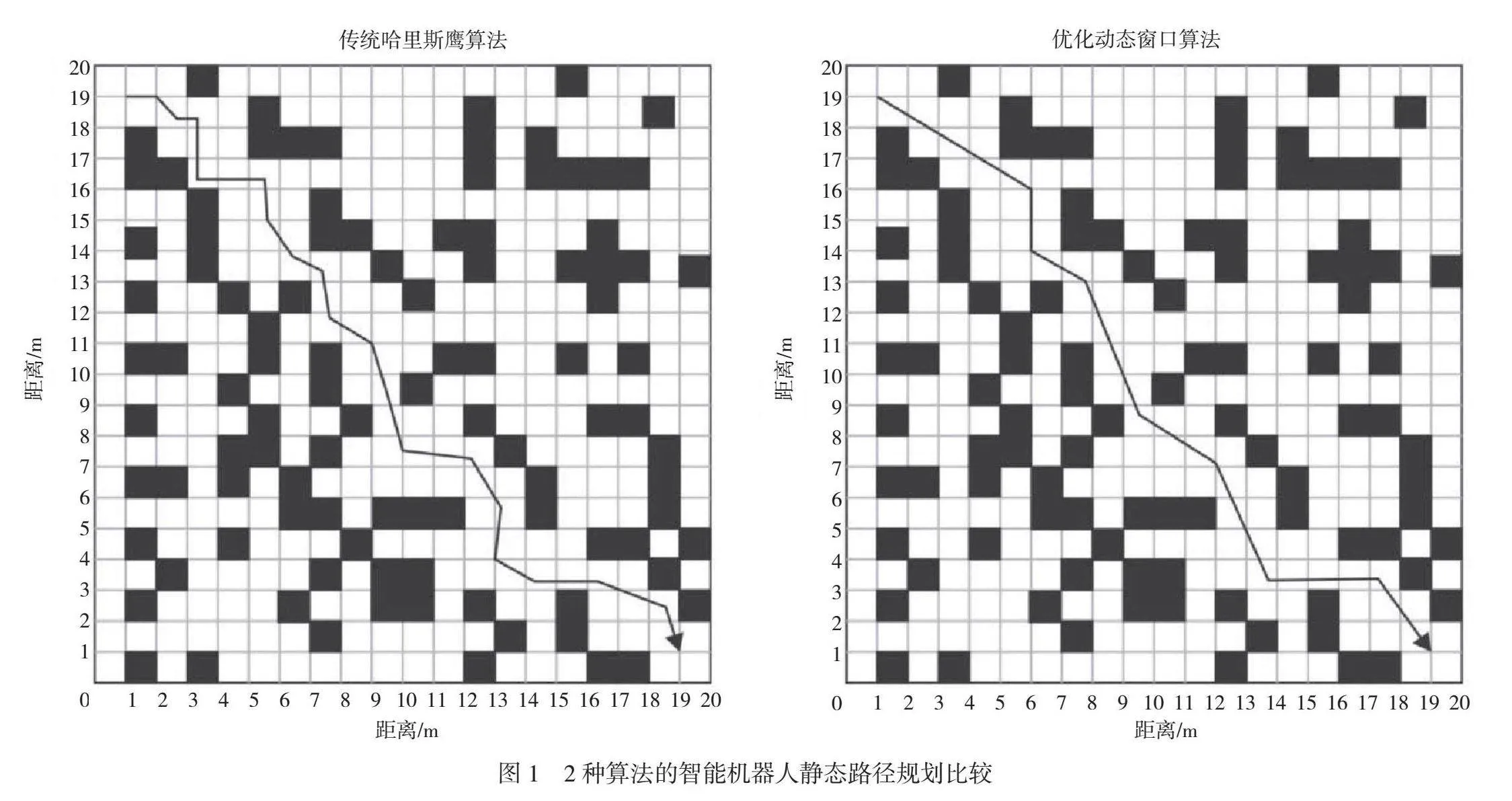
为检验在静态布局地图中路径规划算法的有效性，对2种算法在同一张地图上进行试验，智能机器人静态路径规划比较如图1所示，黑色实线为2种不同算法计算得到的运动轨迹，统计搜索节点数量、路径长度、转折次数、路径节点数量以及时间，2种算法性能比较见表1。由表1可知，传统哈里斯鹰算法规划的路径冗余点与转折次数较多，当运动时会搜索许多节点，导致运行效率显著降低；优化动态窗口算法规划的路径冗余点与转折次数较少，与传统哈里斯鹰算法相比，其运行效率具有一定优势。

虽然2种算法目标点相同，但是优化动态窗口算法参与搜索的节点数量减少了18个，时间也缩短了1.33 s；对关键节点进行深度筛选后，路径节点数量减少了11个，转折次数减少了10次。优化动态窗口算法能够减少转折次数和搜索节点数量，节约计算时间。

4.4 动态路径规划试验

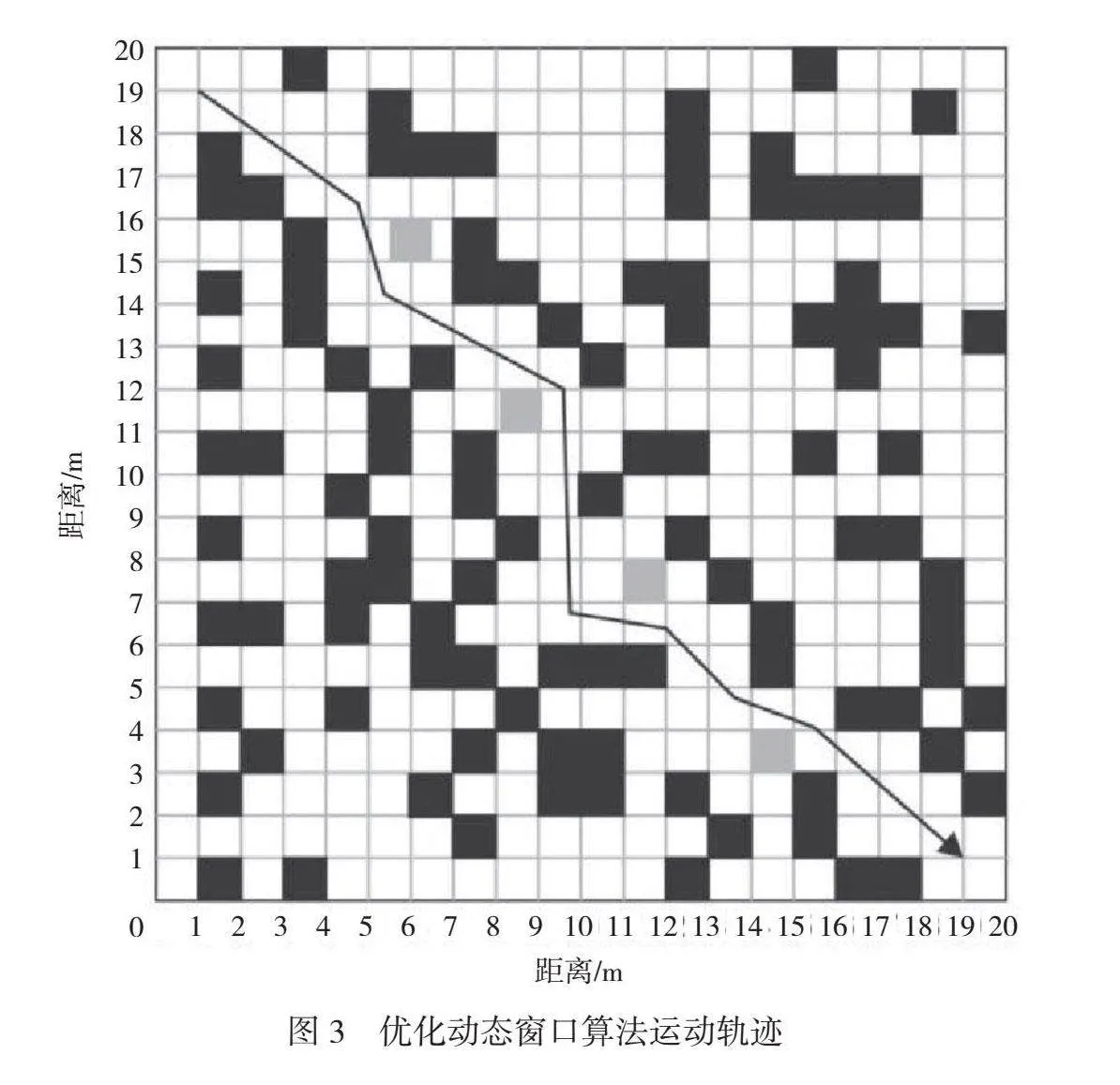
在栅格地图的优化动态窗口算法的运动轨迹上放置灰色模块作为新增障碍物（如图2所示），并将2种算法进行对比试验，由此验证优化动态窗口算法的避障能力，优化动态窗口算法运动轨迹如图3所示。

由图3可知，如果新增障碍物处于全局最佳路径，那么传统哈里斯鹰算法不能有效避障，动态性能欠佳；优化动态窗口算法所得路径在规避了所有新增障碍的基础上更顺滑，符合双轮差速机械结构的运动特点，获得了优质运动轨迹，证明了算法的有效性。

5 结语

综上所述，当优化动态窗口算法应用于动态环境时，可显著减少节点数量，提高运行效率，对关键节点进行深度筛选后能够减少转折次数，解决了当运动时无法躲避新增障碍物的问题，提升了轨迹顺滑度，保证在最佳全局路径上，机器人可实时避障。本研究仅在新增障碍物的环境下进行仿真试验，未过多关注移动障碍物，在后续研究中可将其作为参照，提升应用效果。

参考文献

[1]黄敬尧，刘洪宇，武慧慧，等.基于改进的五行环算法的移动机器人路径规划[J].传感器与微系统，2023，42（10）：143-146.

[2]杨帆，李玮，严天宏.基于梯度优化的移动机器人路径规划算法[J].现代电子技术，2023，46（21）：99-104.

[3]黄勇强，刘砚菊，宋建辉，等.基于改进A*算法与优化DWA的差速移动机器人路径规划[J]. 沈阳理工大学学报，2023，42（6）：25-33.

[4]常新中，岳哲鹏，郜海超，等.基于改进粒子群的混合金豺优化算法的移动机器人路径规划[J].中原工学院学报，2023，34（4）：24-29.