市政排水管道局部淤堵水力特性研究

摘 要：市政排水系统的有效运行对城市的生态环境、居民生活质量以及基础设施的可持续发展至关重要。本文通过数值模拟方法建立排水管道数值模型，探究了干管工况下淤堵物上、下游截面所受冲击力的变化、不同坡度对冲击力的影响以及湿管条件下积水和淹没工况淤堵物所受冲击力和切应力的变化。结果表明，干管工况下，水流流量和坡度越大，淤堵物所受冲击力越大；湿管工况下，淤堵物所受冲击力小于干管工况，冲击力大小与淤堵物露出水面的高度存在显著的线性关系。

关键词：市政工程；排水管道；局部淤堵；水力特性

中图分类号：TU 992" " " 文献标志码：A

在长期运行过程中和多种因素的共同作用下，市政排水管道会出现局部淤堵现象，导致排水能力下降、水流阻滞以及环境污染等。局部淤堵是指排水管道内部的某些区域由杂物、沉积物、污泥等积聚造成的管道截面流通面积变小，水无法顺畅流动[1]。局部淤堵不仅会影响正常的排水功能，还会加剧污水倒灌、管道腐蚀和排水设施损坏等问题，进一步危害城市环境和居民的健康[2-3]。因此，本文依托某市排水管道局部淤堵情况，探究了不同工况下淤堵物的受力变化，研究成果将为城市排水管道规划、建设和管理提供科学依据，促进城市排水系统的可持续发展。

1 工程概况

本文以某市排水系统中的一段排水管道为研究对象，该排水管道直径为200mm，选取段长10m。通气管直径60mm，长度为500mm，设置在距离管道上游入口1m处，淤堵物设置在距离上游入口5m处，其长度为120mm，淤堵物高度根据工况设置。

2 相关理论及数值模型

2.1 控制方程及湍流模型

VOF多相流模型是用于描述流体界面行为的计算流体力学模型。在多相流中，液体、气体和固体颗粒等可以共存并在空间中交互作用。在VOF模型中，流体的体积分数表示每个空间单元内各相占据的比例，即一个空间单元内占据该单元的液体或气体的比例。通过追踪不同相的体积分数分布，可以模拟流体界面的运动、扩散、合并以及分离等现象，体积分数的输运方程如公式（1）所示。

（1）

式中：t表示时间；a为体积分数；ui和xi分别表示不同方向上的流速和笛卡尔坐标系下的坐标。

雷诺平均模型是计算流体力学中常用的一种湍流模型，用于模拟湍流流动中的平均流场，通过将流场中的各物理量分解为时间平均值和湍流分量，将原始的非稳定方程分解为平均方程和湍流应力项，如公式（2）所示。

（2）

式中：μ和μT分别表示动力黏度和涡黏性系数；p为压强；ρ为流体密度。

2.2 数值模型与工况设置

根据实际工程排水管道物理模型建立数值模型。对模型进行网格划分时选取六面体结构化网格，对近壁边界层采用蜂窝状网格进行划分，以更好地捕捉边界层效应。在淤堵物部位增加网格密度，以提升计算结果的精度。排水管道局部数值模型图如图1所示。划分网格后，需要对其进行网格独立性分析，验证网格分辨率对模拟结果的影响。网格数量增长倍数为1.3，模型划分网格后的网格数量分别是221万、260万和311万，计算时间步长分别为0.0003s、0.0006s和0.0009s。比较试验数据与数值模拟结果可知，网格数量与时间步长对模拟结果精度的影响较小，可以忽略不计。结合计算时长，最终选取网格数量为260万、时间步长为0.0009s进行模拟。分别在淤堵物和排水管道内壁布置5个测点和2个测试截面，其中侧点1位于淤堵物上游、测点2、3、4位于淤堵物部位，测点5位于淤堵物下游。

工况设置见表1，分为A、B、C共3组工况，将A组和B组边界条件设置为恒定流量入口，C组边界条件设置为非恒定流量入口。A组初始水位为0mm，即模拟干管条件下，恒定水流对淤堵物的冲击作用；B组初始水位为0mm～40mm，以探究恒定水流对淤堵物的影响；C组管道具有基础流量，其数值为1L·s-1～15L·s-1不等，模拟非恒定水流对淤堵物的影响。此外，设置基础流量为30L·s-1，以探究满管工况下非恒定水流对淤堵物的水力作用。

3 计算结果分析

3.1 干管条件下水流冲击障碍物分析

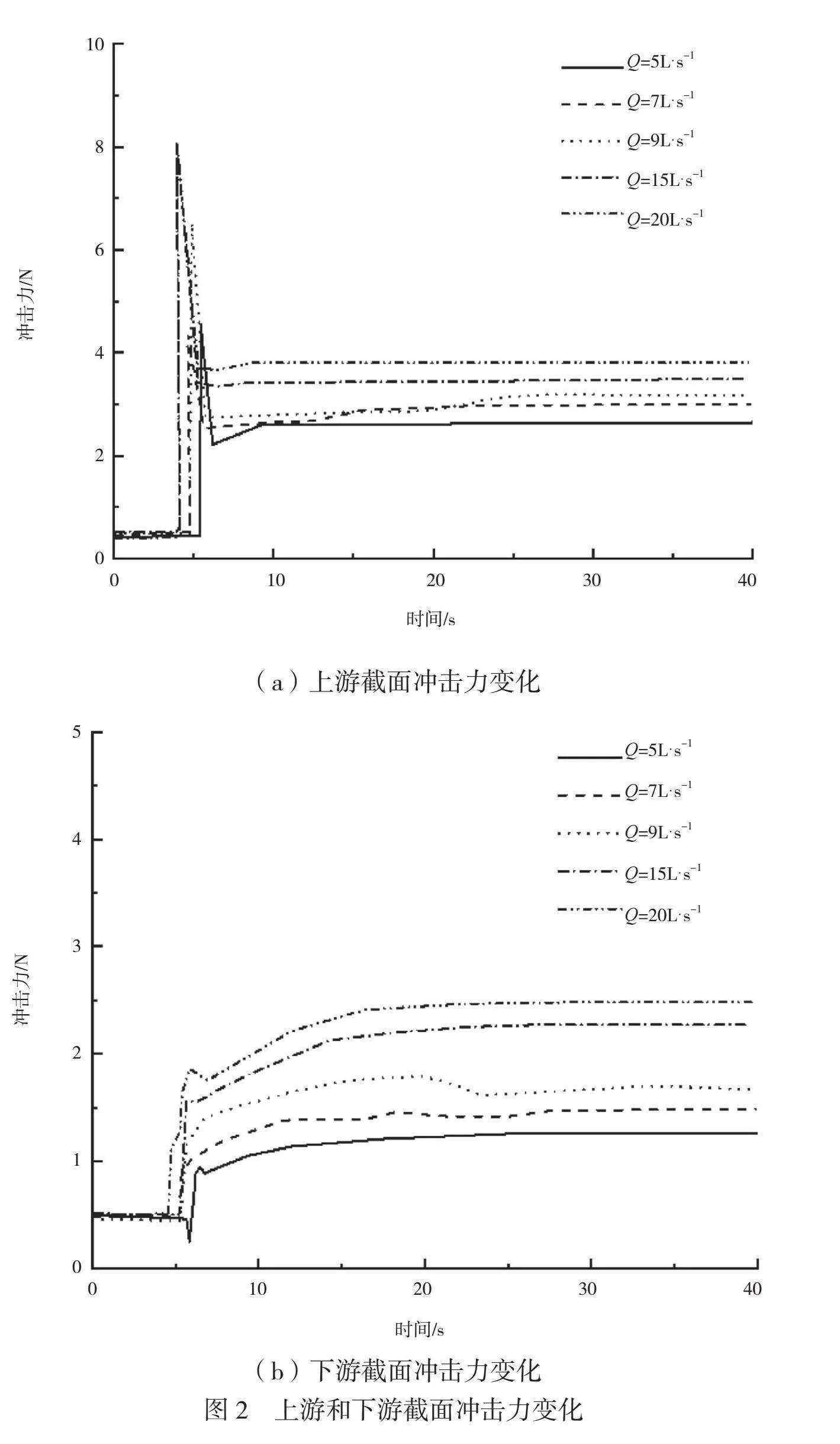
淤堵物上游和下游截面冲击力随时间和水流流量的变化如图2所示。观察图2（a）可知，在淤堵物受到水流冲击的瞬间，其所受冲击力瞬间增加，然后迅速回落，随着时间的推移逐渐趋于稳定。此外，根据不同水流流量下的冲击力变化可知，水流流量越大，对淤堵物的冲击力越大。由图2（b）可知，淤堵物下游截面受水流冲击时，其冲击力瞬间增加，然后缓慢增加并逐渐趋于稳定，不同水流流量下的冲击力变化规律与上游截面一致，水流流量越大，冲击力越大。根据水流流量为9L·s-1时的淤堵物压强分布可知，淤堵物中部和底部压强较大，而两侧边缘部位压强相对较小。原因是流体以不同速度在某区域内流动时，流体的动能和压强处于平衡状态。在水流中，流速较大的地方压强较低，流速较小的地方压强较高，当水流冲击淤堵物时，两侧流速会增加，导致压强降低，而在淤堵物的中部和底部，水流速度较小，从而压强相对较高。

在不同水流流量下，水流与淤堵物相互作用的过程可看作射流冲击过程，因此可根据公式（3）计算水流的最大冲击力。

F=KρAv2 （3）

式中：v表示水流流速；A为受力面积；K为修正系数；F为冲击力。

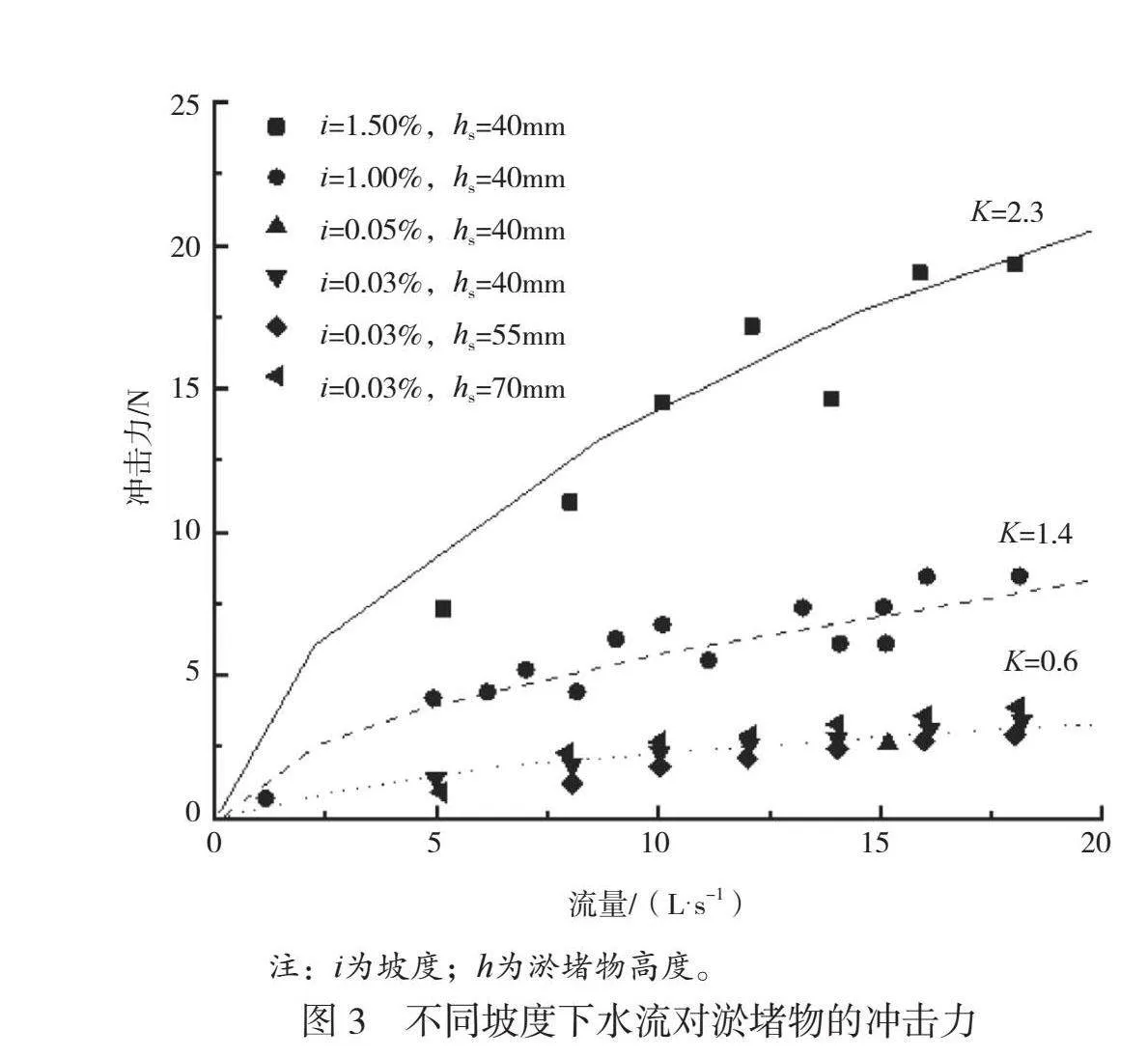
在实际情况中，流体的行为受许多因素影响，如淤堵物的几何形状、表面粗糙度、流体的黏性以及流速分布等。考虑这些因素对计算结果的影响，本文引入了修正系数K，使其更适用于特定情况。当水流流量为一定大小时，淤堵物的受力面积接近自身的截面面积，不再发生变化，此时水流的冲击力主要受流速的影响。当管道直径、水流流量、管道材质和粗糙度等因素相同时，水流流速主要取决于坡度的大小。不同坡度下水流对淤堵物的冲击力如图3所示。从图3可以看出，当淤堵物高度一定时，坡度越大水流对淤堵物的冲击力越大，此外，不同坡度计算结果的修正系数不同，当坡度为1.5%、1%、0.05%和0.03%时，修正系数分别取2.3、1.4和0.6，理论计算值与数值模拟值吻合度较高，因此坡度越大，修正系数K的值越大。当坡度、水流流速和流量一定时，不同高度淤堵物所受水流冲击力相差不大。

3.2 湿管条件下水流冲击障碍物分析

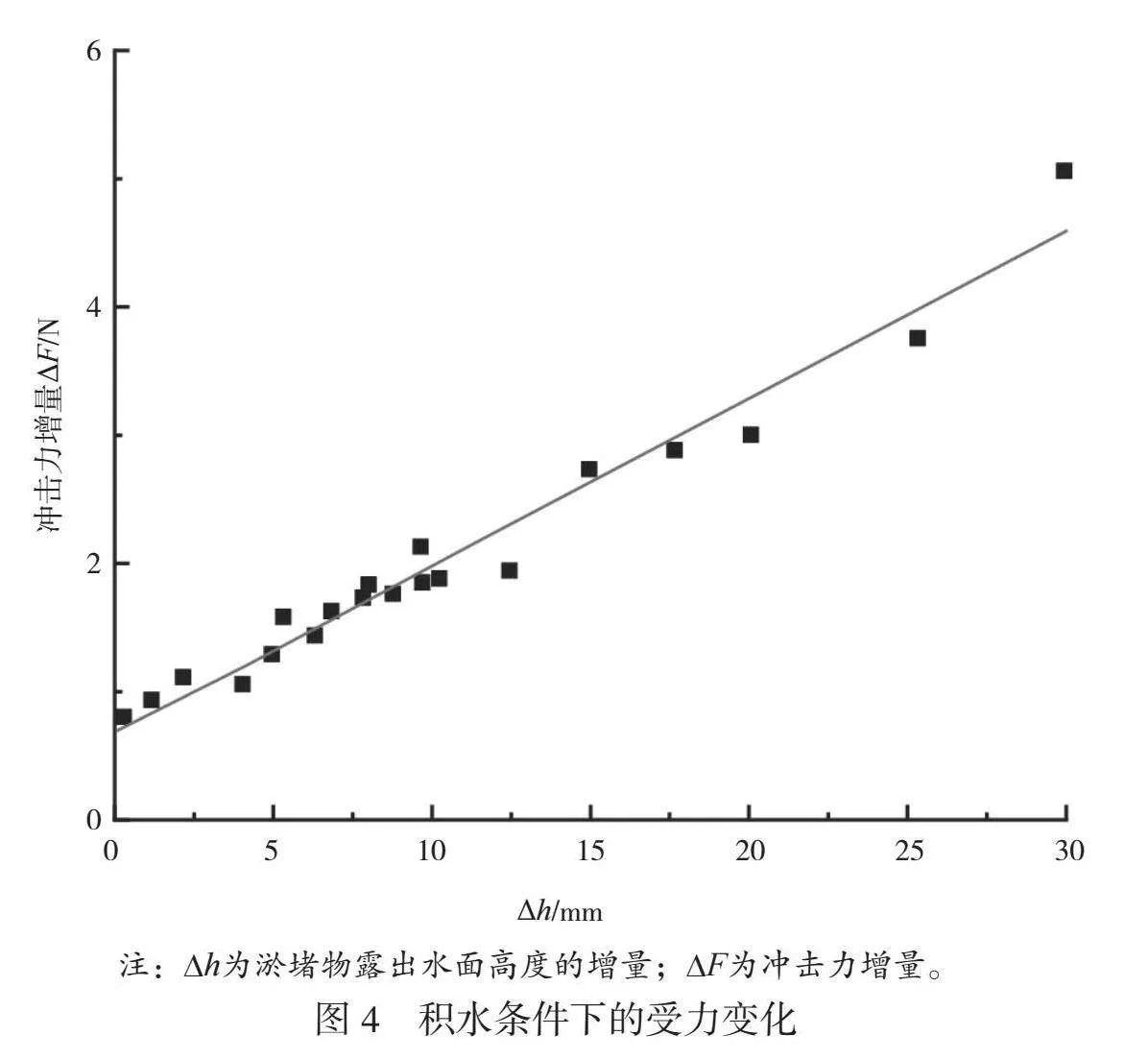
管道内积水情况下淤堵物冲击力变化如图4所示。由图4可知，随着淤堵物露出水面高度的增加，其所受水流冲击力不断增大，淤堵物露出水面高度与水流冲击力间存在显著的线性关系。原因是淤堵物裸露高度越大，与水流间的相互作用越强烈，更多的水流动能转化为冲击力，从而使其所受冲击力增加。因此，当管道内水位流量一定时，可以通过淤堵物露出水面的高度预测其水流冲击力，通过对计算结果进行线性拟合可以得出两者近似满足公式（4）。

ΔF=12.76Δh+0.69 （4）

淤堵物完全淹没情况下的受力情况如图5所示。随着基础流量的增加，淤堵物所受冲击力增大，但增加幅度较小。由基础流量变化导致的冲击力变化显著小于干管情况下的冲击力，当基础流量近似等于17L·s-1时，干管工况下的冲击力约为湿管的7倍。原因是在湿管工况下，基础流量使管道内的水流相对平稳，流速较低。相比下，干管工况下的水流更趋于湍流，增加了动能传递，进而增加了冲击力。

4 结论

为探究不同工况下水流冲击对淤堵物受力特性的影响，本文采用数值模拟方法对干管和湿管条件下水流冲击淤堵物的受力特性进行了分析，所得结论如下。1）干管条件下，淤堵物上游截面所受冲击力随时间变化呈先瞬间增加、后迅速变小、再趋于稳定的趋势；下游截面所受冲击力先瞬间增加，然后缓慢增加并逐渐趋于稳定；水流流量越大，淤堵物截面所受冲击力越大。2）干管工况下，淤堵物中部和底部压强较大，而两侧边缘部位压强相对较小。当淤堵物高度一定时，坡度越大，水流对淤堵物的冲击力越大。不同坡度冲击力计算结果的修正系数不同，坡度越大，修正系数值越大。3）湿管条件下，淤堵物露出水面高度越大，所受水流冲击力越大。由基础流量变化导致的冲击力变化显著小于干管条件下的冲击力。

参考文献

[1]桑浪涛，石烜，张彤，等.城市污水管网中污染物冲刷与沉积规律[J].环境科学，2017，38（5）：1965-1971.

[2]张健，方杰，范波芹.VOF方法理论与应用综述[J].水利水电科技进展，2005（2）：67-70.

[3]董淑芳，何同溪.曼宁公式在管道水头损失计算中适用性的讨论[J].山东建筑工程学院学报，1998（1）：104-107.