发动机总装车间中转库房布局优化

摘 要：本文针对发动机总装车间的中转库房的布局和约束条件，采用自适应变异粒子群算法进行求解，得出中转库房的更优布局。考虑工位物料消耗时间将总装线有效工位进行分组，根据分组对中转库房进行分区，抽出合理的数学模型，通过比较可知，优化后的搬运时间明显降低，提高了中转库房的运作能力。通过实际数据的应用验证了模型和算法的有效性，中转库房的分区思想有明确的改善效果，可以作为实际车间布局的参考。

关键词：车间优化布局；粒子群算法；仓库规划

中图分类号：TH 181" " " " " " 文献标志码：A

库房布局优化是现代制造企业面临的重要且复杂的问题之一，合理的总装车间中转库房布局能够提高生产效率并降低制造成本[1]。实际汽车制造企业对中转库房内的物料摆放不够重视，造成配送过程中的物流浪费。因此，很多企业开始重视对中转库房布局的研究。

很多学者对车间中转库房布局优化进行相应的研究。董舒豪等[2]用传统的系统布置分析法（Systematic Layout Planning）对不同区域间的物流量关系强度进行分析，从而对传统车间布局不足的问题进行优化，并用仿真分析的方法进行弥补；Wang等[3]利用遗传算法来解决以总成本最小为目标函数的布局规划模型；卢义桢等[4]用自适应遗传模拟退火算法对车间设施布局问题进行求解，给出了公司的车间设施布局优化案例。

本文以实践应用为视角，分析发动机总装车间中转库房布局现有存在的问题，根据约束条件结合实际情况抽出合理的数学模型。以最短配送时间为目标函数，采用适用模型的自适应粒子群算法使求解过程更精准，得出的优化结果验证了方法的有效性。本文结论对加快物料流通，对实际总装车间中转库房的布局优化问题有指导意义。

1 中转库房布局规划

1.1 现有库房布局问题现状

由于总装车间物料繁多，现有发动机总装车间中转库房原有物料布局是随意的，主要通过员工经验等主观因素进行摆放。当物料配送时需要小车在整个中转库房大范围拣货，再根据地面物流通道按固定的顺序到相应的各工位运送一圈回到库房，影响配送效率和时间。需要对中转库房布局进行规划。

1.2 以工位组合的布局分区思路

以工位为中心进行整合的分区思路是库房内物料依据生产计划确定的每个工位的物料需求量和操作时间进行分组。分区内将工位组合所需全部物料按照工序成套安放，配送小车在分区内装货配送到总装配线上，中转库房内的物料以箱为单位进行假设。假设1和7工序的工位操作时间耗时相同，就可以将1和7组合成一个组，将物料放到同一个分区内。中转库房分区内直接对应相同节拍工位的物料配送，减少小车在中转库房的作业时间，可以明显提高效率。

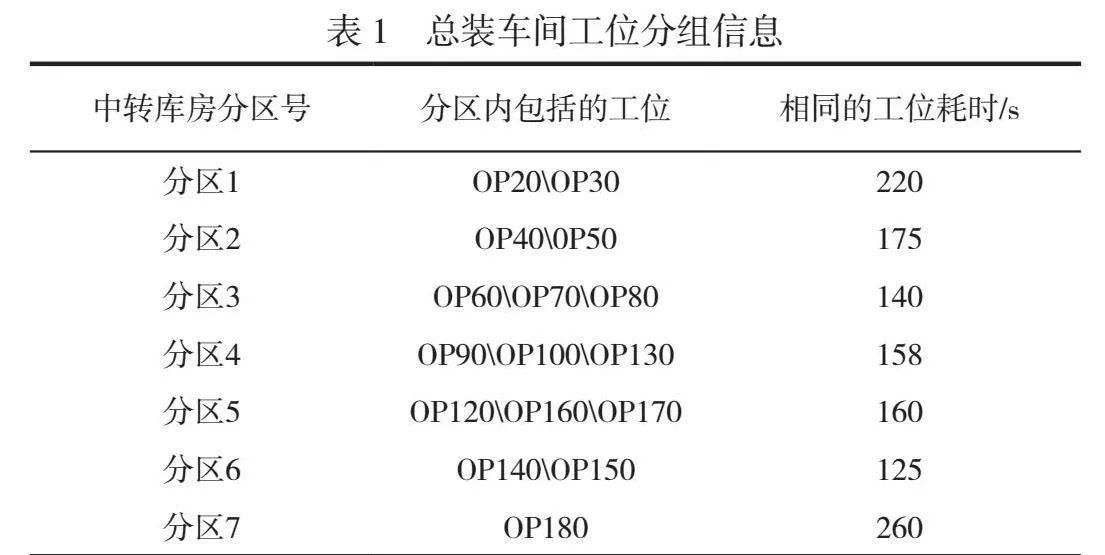
文中以总装线的工位消耗时间作为主要分区依据。根据实际情况，总装线共设有22个装配工位，总成装配线呈环形布置。由于气缸线上线、外观检查、气密性测试、安装变速器总成、发动机总成下线以及小车送回6个工位没有物料运输需求的环节，因此缩减记成16个工位，并将16个工位根据生产计划内容进行整合。总装车间中转库房被规划整合为7个分区，分区内包括的工位见表1，耗时相同的工位所需的物料全部存放在同一个分区内。

1.3 存储区布局规划的数学建模

1.3.1 模型假设

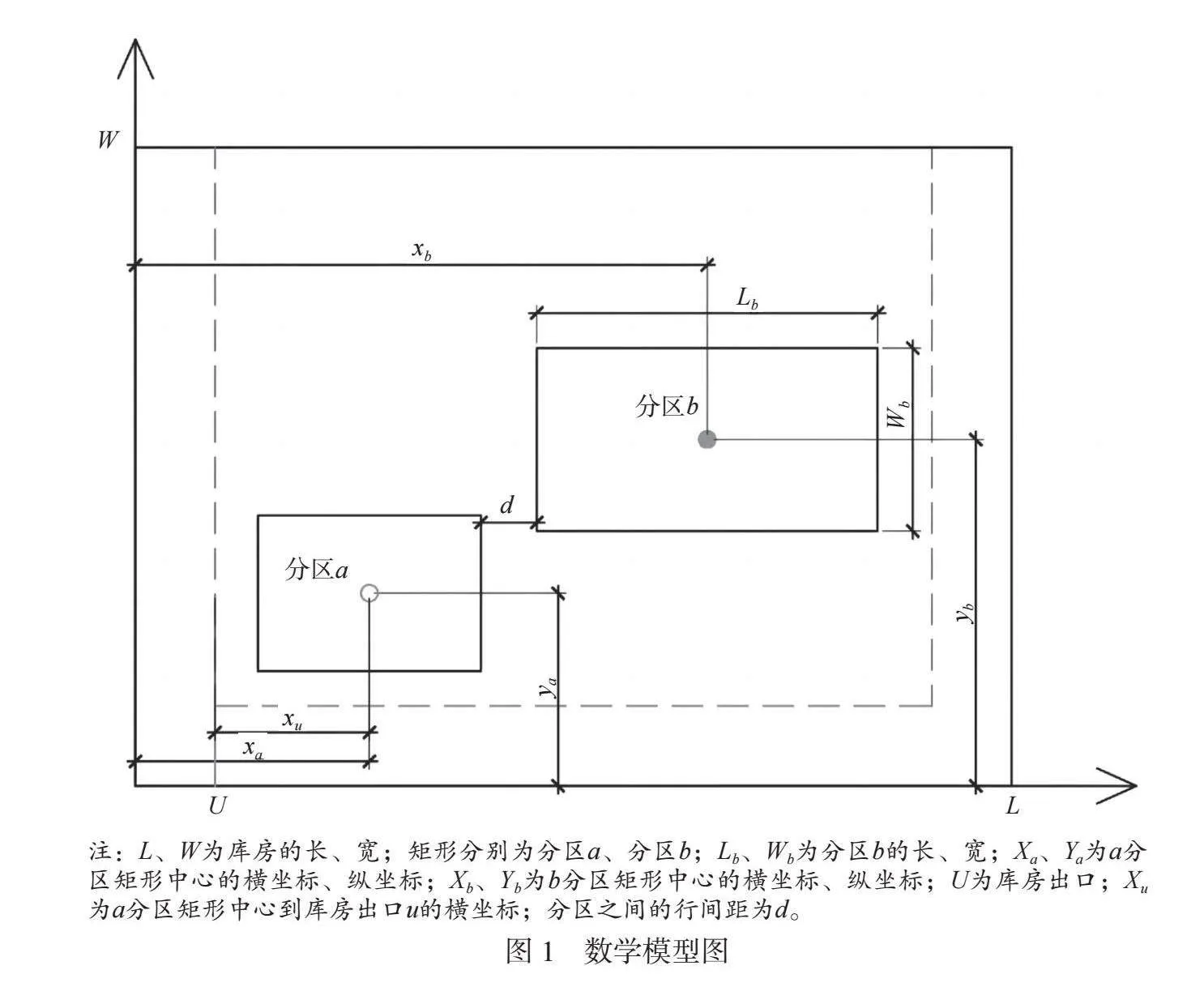
为了研究多行设备布局问题，本文对实际的车间库房布局进行了简化，模型假设如下。1）假设库房分区后的各分区形状均为长和宽均已知的标准矩形。在X轴上横向平行，在Y轴上纵向平行。2）考虑到库房内四周需要预留物流通道，假定各分区都在一个虚拟的矩形空间固定矩形空间，空间与库房四周墙壁的左下距离为固定值。3） 矩形空间按布局需要，以宽度不等，分成若干行。4）分区矩形之间的距离受空间约束是固定值，取决于边缘最近的2个分区矩形的距离。5）假设小车搬运物料的路径与车间边界相互平行。搬运小车一次只服务1组工位，从分区内取出对应的组合所需的全部物料。建立数学模型如图1所示。

1.3.2 模型构建

数学模型的目标函数及约束条件如公式（1）～公式（9）所示。

（1）

[Qau]=M·K （2）

（3）

（4）

（5）

（6）

（7）

（8）

xa、ya≥0，a=1...n" " " （9）

式中：n为分区的个数；u为库房出口、M为小车固定物料量；m为总装线数量；[Qau]为分区a到库房出口u的物流量；Dau为分区矩形中心坐标a到库房出口u的直角距离和；Vij为人工推车运行速度（按平均速度取值）；Diu为库房出口至总装线的物流通道总长度；K为中转库房分区的搬运频次；xa和xb为a、b分区矩形中心的横坐标[5]；Posxa和Posya分别为中转库房分区矩形中心a的横坐标矩阵和纵坐标矩阵；k为空间内行数，zak为决策变量。

式（1）表示总配送时间最短的数学模型的优化目标；式（2）表示各中转库房分区矩形到中转库房出口的物流量；式（3）表示各中转库房分区矩形到库房出口的直角距离，即两点间的直角距离等于纵坐标差的绝对值加上横坐标差的绝对值之和；式（4）表示分区矩形横坐标的约束条件，以防分区矩形在水平方向重合；式（5）为分区矩形纵坐标的约束条件，不同行的分区矩形在竖直方向保持距离[5]；式（6）和式（7）将中转库房分区矩形限制在布局场所内；式（8）和式（9）表示每个作业单位只出现一次。由于限制了总装车间中转库房的大小，因此将长设为L、宽设为W。

1.4 粒子群算法及改进

粒子群算法[6]（Particle Swarm Optimization， PSO）是Eberhart博士提出的一种模拟鸟群飞行觅食的具有启发式特征的随机搜索算法。在D维的搜索空间中，总粒子数为n，每个粒子和每个粒子对应的速度分别表示为xi和vi，第i个粒子在迭代过程中追随自身的个体最优值Pbest表示为Pi，粒子群截至目前搜索到的全局最优位置为Pj，称为群体全局最优值Gbest。式（10）为第i个粒子[7]在D维中经历k次迭代的粒子速度和位置的更新公式，如公式（10）所示。

vidk+1=wvidk+c1r1（Pi-xidk）+c2r2（Pj-xidk）

vidk+1=xidk+vidk+1 （10）

式中：w为惯性权重；c1为个体加速因子，c2为群体加速因子；适当的加速因子可以防止陷入局部最优的状态；r1 和 r2为[0，1]相互独立的随机数。

1.4.1 自适应变异粒子群算法

由于自适应变异粒子群优化算法结合了粒子群算法和变异操作，对解空间进行全面探索以及具有更好的收敛性能，能够更快地找到全局最优解或接近最优解，从而找到更优的布局结果，因此本文在考虑布局优化问题上引用自适应变异粒子群算法更合适。大部分粒子追随可行空间的最优粒子而运动，容易陷入过早收敛，将自适应变异机制引入粒子群算法中，防止出现过早收敛的情况。对粒子群算法在如下方面进行改进：自惯性权重的调整。自适应权重[8]是指根据算法所处的状态动态调整权重的一种策略。如果某个参数的历史梯度较大，则学习率就会被缩小，以避免步长过大而错过最优解。式（11）中自适应权重可以使算法更智能地选择每一次迭代更新时的权重，从而提高算法的性能，如公式（11）所示。

w=wa-（wa-wb）Ni/Nmax （11）

式中：Nmax为最大迭代次数；Ni为当前迭代的次数；wa为初始惯性权重；wb为粒子迭代最大的惯性权重。

1.4.2 粒子变异

引入变异粒子也要根据种群的聚集程度来决定，这样才能允许粒子在算法被卡住的情况下朝着新的方向进行搜寻。变异概率的大小会随σ2的变化而变化，这里采用的变异概率pm如公式（12）所示。

（12）

式中：pm为群体最值的变异概率；σm2为适应度方差在第m次迭代；Pmax、Pmin为目前变异概率的最大值、最小值。式（12）可以看出，适应度方差和全局极值的变异概率呈反比关系[8]。算法可以根据群体中粒子的位置状态自适应的调整变异概率，避免局部最优解。

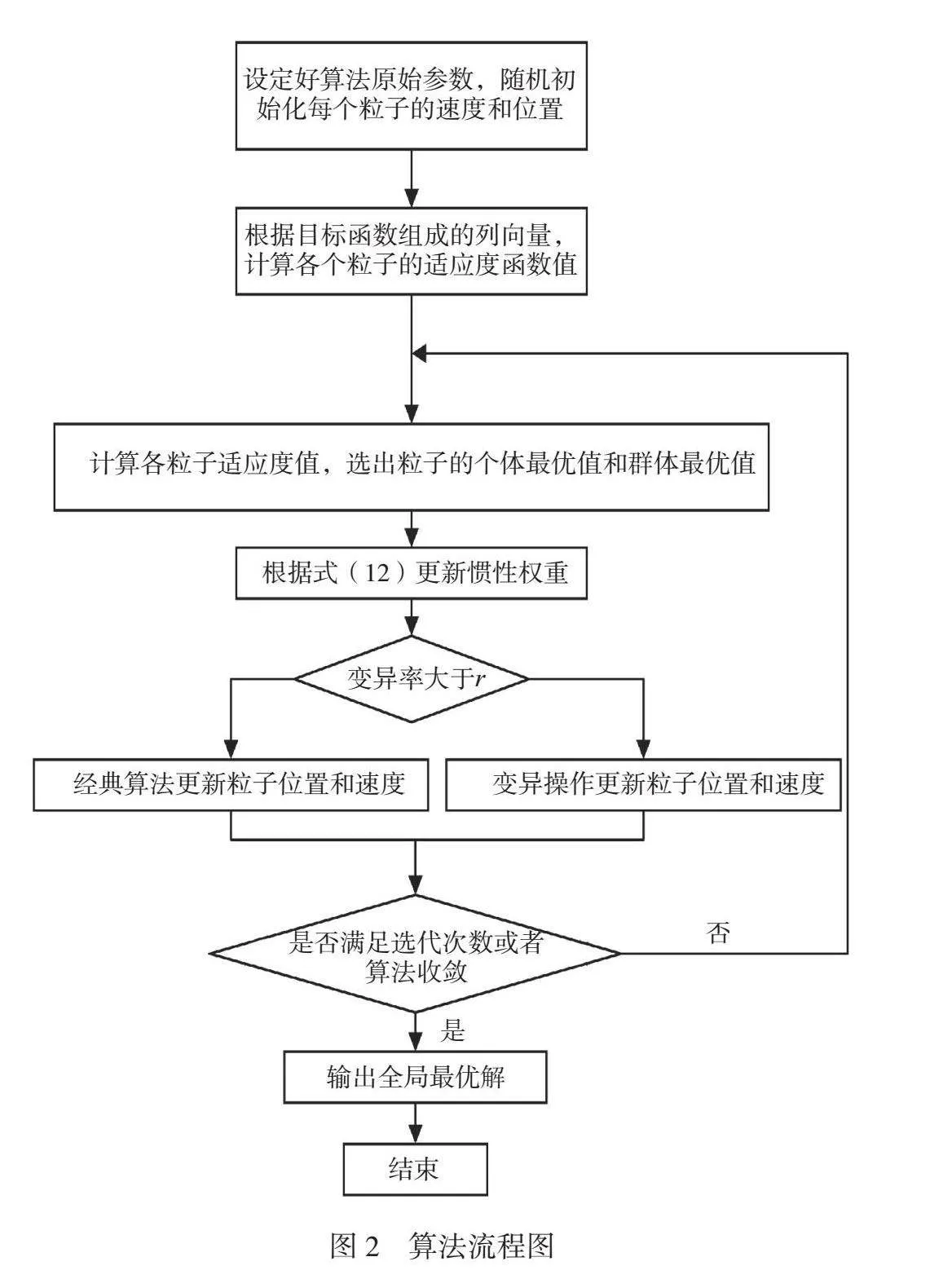
由于粒子的全局速度随着迭代越来越低，一开始先形成全局搜索，当接近收敛时粒子速度降低，使粒子在近似最优解的局部充分搜索，权重阻尼系数取0.99。文中自适应变异算法流程如图2所示。

2 数值实例和结果分析

2.1 数值实例

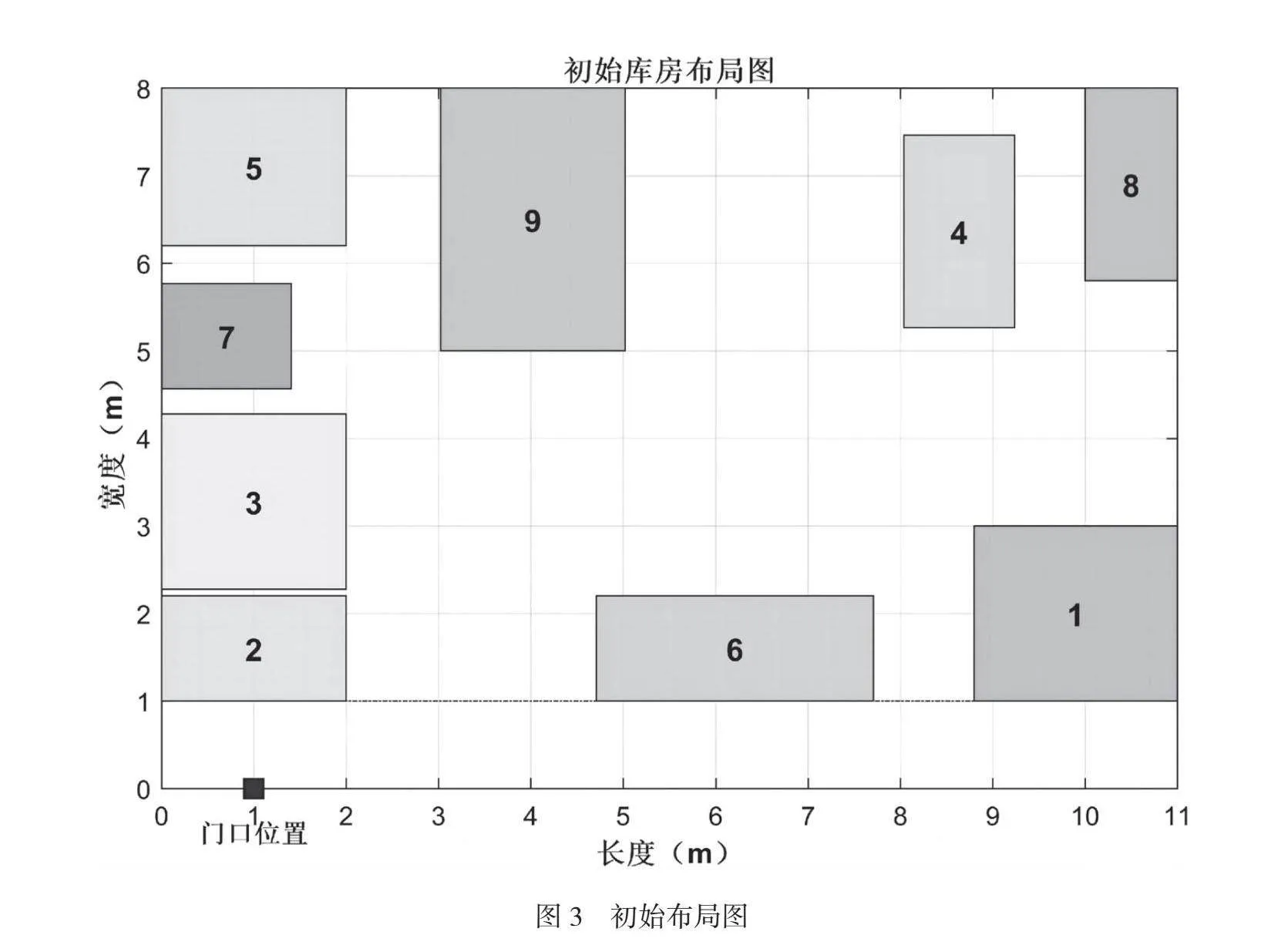
F发动机总装车间中转库房是长度为11m、宽度为8m的矩形仓库。仓库有出口门，采用单边进出的方式，仓库出口的坐标是固定的，具体实际约束条件和文中假设状态见表2。F公司总装车间中转库房的原有布局是无序的，物料混乱摆放的。初始库房内物料按照种类和体积记作九个区域，初始化布局如图3所示。原始布局的序号仅代表物料摆放的位置，不代表分区。用改进算法进行求解所得的一组坐标就是优化后的各矩形最优位置的中心坐标。

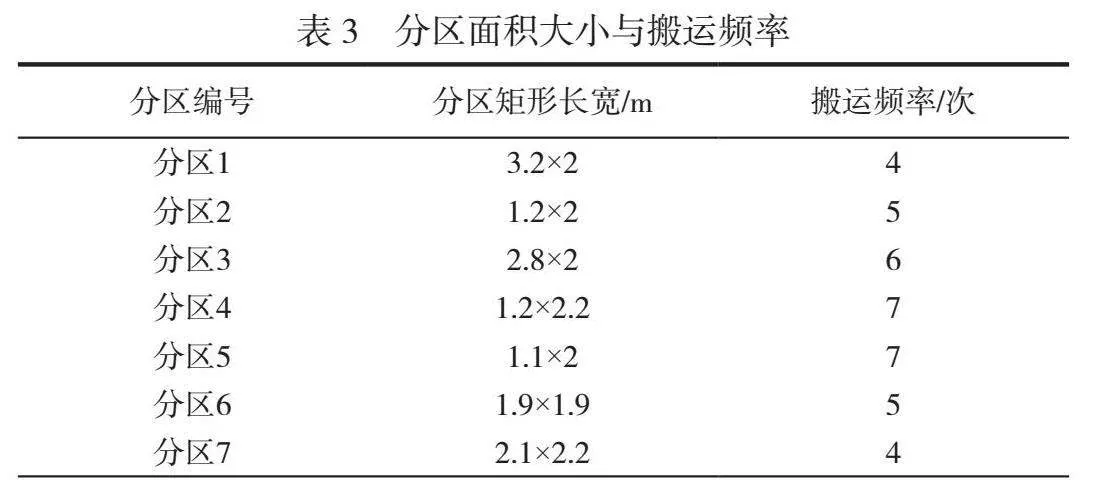
库房至装配线的小车走的物流通道长度（这里假设仓库外配送距离都是固定值）39m，小车的最大装载容量以体积为单位，设q为30。由于一个小车的物流量就是存储区内各分区的搬运频次乘以车的满载量，再乘以各分区到出口的距离就是物料分区的总物料搬运量。将总装配线的有效工位按前面发动机总装线工位组合分成7个工位组，将这7个工位编组设为7个大件矩形分区，进行编号并对7个矩形的布局进行满足目标条件的重新排列。将每个矩形的几何中心点作为过程中每个区的优化位置。表3为总装车间中转库房各分区大小以及物料搬运的具体信息。

2.2 结果分析

在MATLAB中编程求解布局优化问题，根据自适应变异粒子群算法的原理以及积累的经验，其主要参数设置见表4。

总装车间中转库房在没有约束条件情况下的各初始位置坐标为{[9.9，2]，[1，1.6]，[1，3.2768]，[8.6384，6.3621]，[1，7.1]，[6.2089，1.6]，[0.70555，5.1674]，[10.5，6.9]，[4.0218，6.5]}。原始布局下的物料搬运最短时间为74925.5472 s。

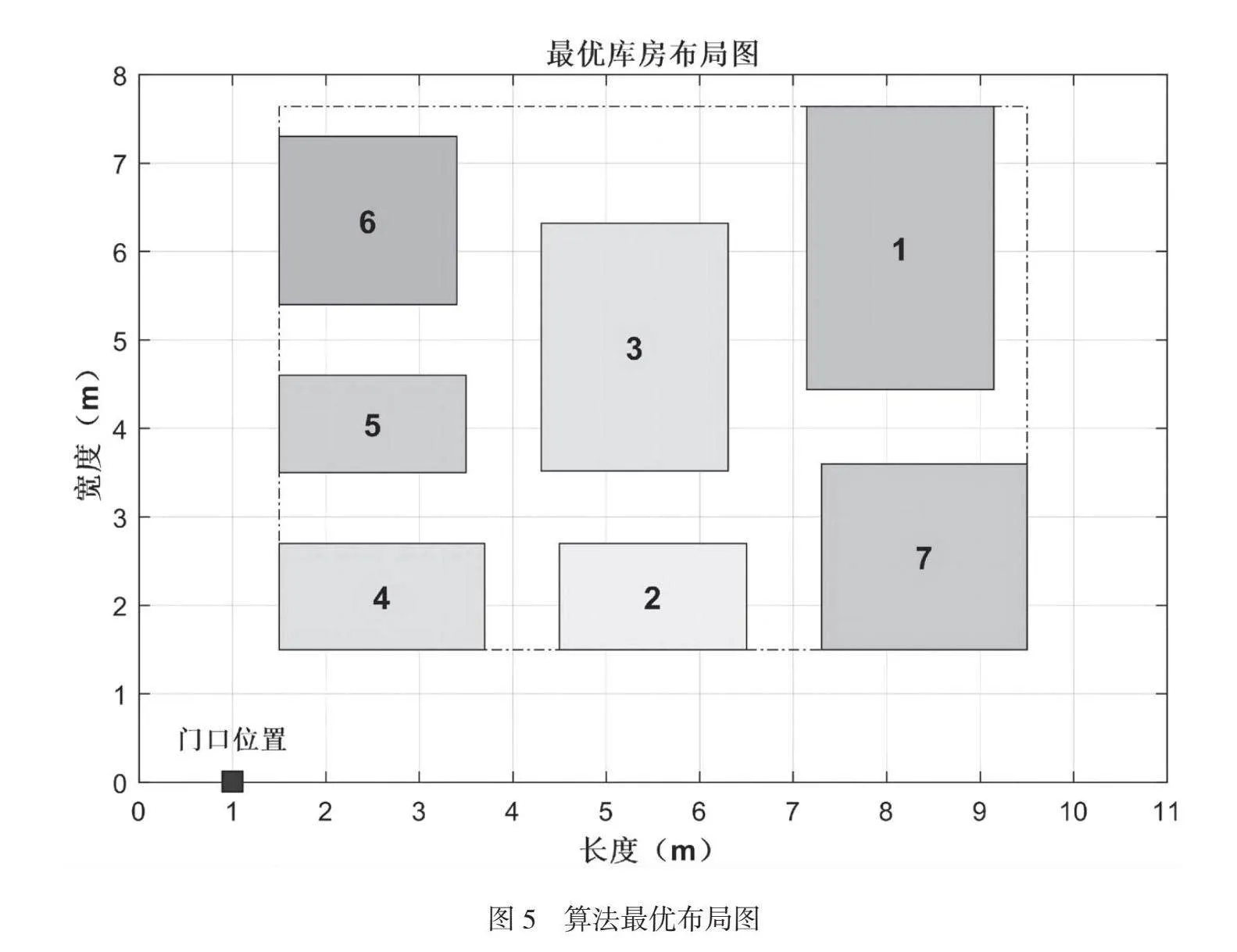
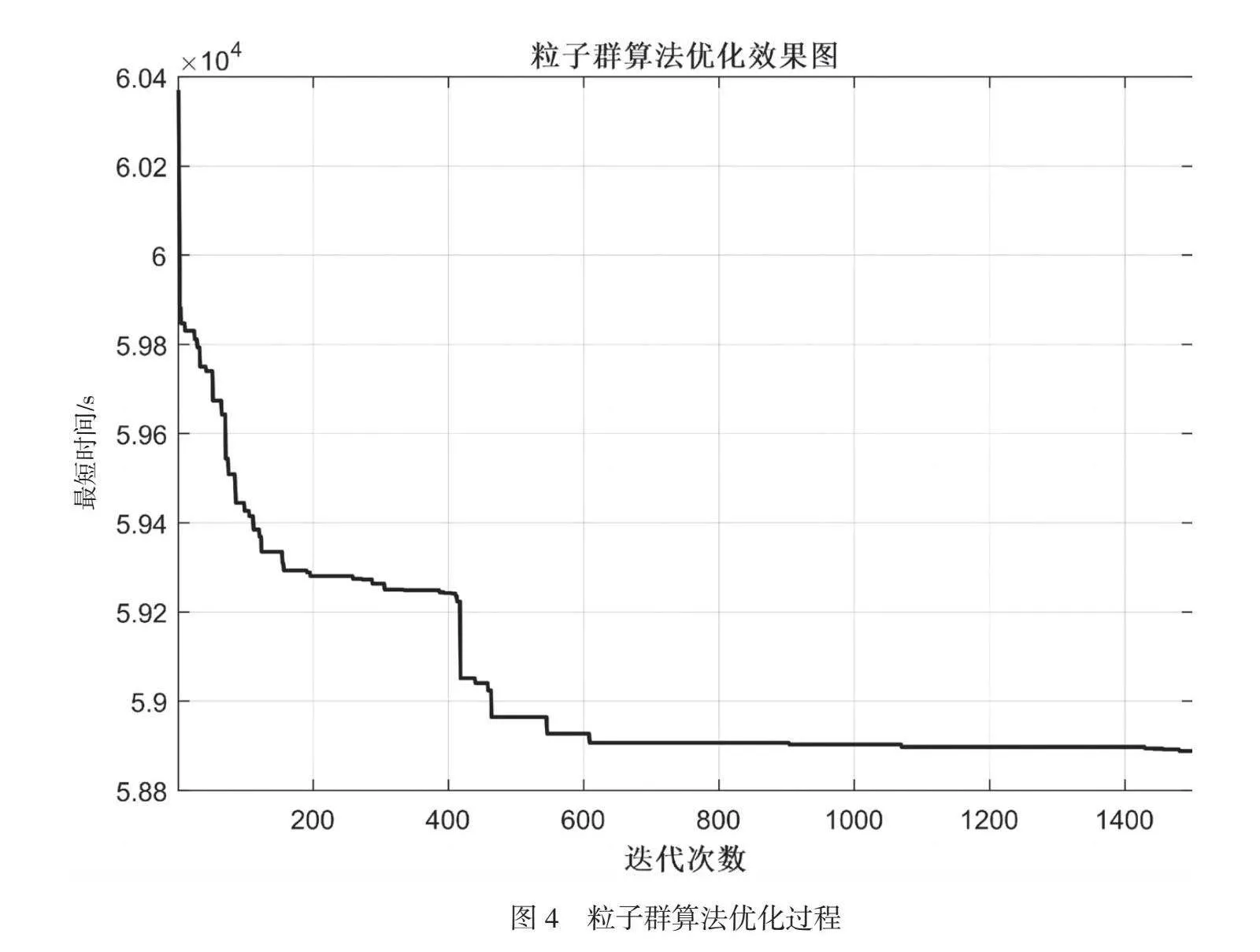
引入自适应权重的粒子群算法经过1500次数的反复迭代的结果如图4所示，从第611次到第1500次迭代的迭代曲线逐渐趋向不变，可以判定此时的值即为近似最优解，此时目标函数的值为58888.2808s。与优化布局之前的搬运时间74925.5472s相比减少16037.2664s的物料搬运时间，优化后效果明显的布局示意如图5所示。由此可知，采用自适应变异粒子群算法得出的结果，总配送时间较初始状态的布局缩短了21.4%。经调整后的中转库房最优布局图中各分区的中心坐标为第1个存储区的中心位置坐标为[8.1456，6.0395]，第2个存储区的中心位置坐标为[5.5，2.1]，第3个存储区的中心位置坐标为[5.3036，4.9195]，第4个存储区的中心位置坐标为[2.6，2.1]，第5个存储区的中心位置坐标为[2.5，4.0507]，第6个存储区的中心位置坐标为[2.45，6.3508]，第7个存储区的中心位置坐标为[8.4028，2.55]。

根据结果表现，采用自适应变异粒子群算法得出的结果，总配送时间较初始状态的布局缩短了21.4%。由此可见，按照工位组合对中转库房布局进行改进优于原始布局状态，该文设计的模型也是科学有效的。

3 结论

针对实际发动机总装车间中转库房布局优化问题，以工位消耗物料的时间为依据，对工位分组进而对库房进行分区建模是可靠的。以最短配送时间为优化目标，不仅考虑中转库房内的物料搬运时间，还考虑仓库外不同物流量会造成的不同影响。用自适应变异粒子群算法进行求解，给出F公司实际中转库房的布局最优图，运行效果显著缩短了21.4%，证明了模型的有效性和分区的想法的可行性，可以为实际企业车间提高市场竞争力。

参考文献

[1]葛晓梅，李世豪.基于改进遗传算法的多目标车间布局优化问题研究[J].现代制造工程，2021（3）：10-14.

[2]董舒豪，徐志刚，秦开仲，等.基于SLP与SHA的农机车间布置优化及仿真研究[J].现代制造工程，2020，2020（1）：50-57.

[3]WANG M J，HU M H，KU M Y.A solution to the unequal area facilities layout problem by genetic algorithm[J].Computers in industry，2005，56（2）：207-220.

[4]卢义桢，李西兴，朱传军，等.基于自适应遗传模拟退火算法的多目标车间布局优化[J].制造技术与机床，2022（7）：173-179.

[5]孟祥超.L企业机加车间设施布局优化研究[D].重庆：重庆理工大学，2020.

[6]贺春光，韩光，赵阳，等.双碳背景下计及新能源大规模接入的电量趋势预测与分析[J].可再生能，2022，40（11）：1554-1562.

[7]邬月春.基于自适应变异粒子群算法的物流配送路径优化[J].兰州交通大学学报，2012，31（1）：114-117.

[8]王铁君，邬月春.基于混沌自适应变异粒子群算法的铁路空车调配[J].计算机应用研究，2011，28（4）：1276-1278，1282.