基于模型预测的无人车辆最优控制

摘 要：随着科技不断进步和人工智能的发展，无人驾驶汽车正逐渐变为现实。它能够自主感知周围环境、做出决策并控制车辆行驶。本文介绍了一个用于控制无人车辆自主转向的智能控制系统，采用非线性模型预测控制（MPC）方法，旨在辅助新手驾驶员安全出行。本文通过研究基于动力学模型的轨迹跟踪控制系统，并应用模型预测控制算法，提高了无人驾驶车辆在复杂工况和多速度情况下的轨迹跟踪准确性和稳定性，具有重要的应用价值。

关键词：无人驾驶汽车；自主转向；智能控制系统；觉感知；模型预测控制

中图分类号：TP 23" " " " " " " " " " " " " " " " " " " 文献标志码：A

无人驾驶汽车是指能够自动行驶和操作而无须人类驾驶员的汽车。它利用各种传感器、计算机视觉和人工智能技术来感知周围环境、分析数据并做出决策，以实现自主导航和驾驶。无人驾驶汽车可以预先设定目的地，也可以根据实时交通情况自主选择最佳路径和行驶方式，同时能够遵守交通规则，配合其他车辆进行驾驶。无人驾驶汽车的目标是减少交通事故、缓解交通拥堵以及提高交通效率和安全性，为人们提供更便捷、舒适的出行方式。

针对场景识别和控制器参数优化的算法层出不穷，为无人驾驶汽车的发展做出了突出贡献。利用神经网络，通过调整动态变化控制器参数，可以增强控制器的泛化能力。模型控制预测（MPC）在许多领域都应用广泛[1-2]，但是其在无人驾驶车辆领域的应用仍然是一个相对较新的研究方向。无人驾驶车辆需要在复杂、动态的环境中实时做出决策，而MPC可以有效处理这类问题，因此本文将MPC应用于无人车的控制。

1 无人车的数学模型

无人驾驶汽车的数学模型描述汽车如何响应其控制输入以及如何与环境互动[3]。为实现无人驾驶车辆的优化控制器设计，需要对无人车进行物理建模，构建其数学模型。本节将深入探讨无人车的自行车模型，并指出其中的约束条件。

1.1 无人车动力学建模

基于上述感知模块以及决策模块，无人驾驶车辆可以获取多种传感器信息，例如周围车辆、行人信息和基于多线激光雷达的障碍物深度信息等。根据这些数据，本文将对无人驾驶车辆进行动力学建模，随后进一步探讨车辆感知信息的预测控制方法。

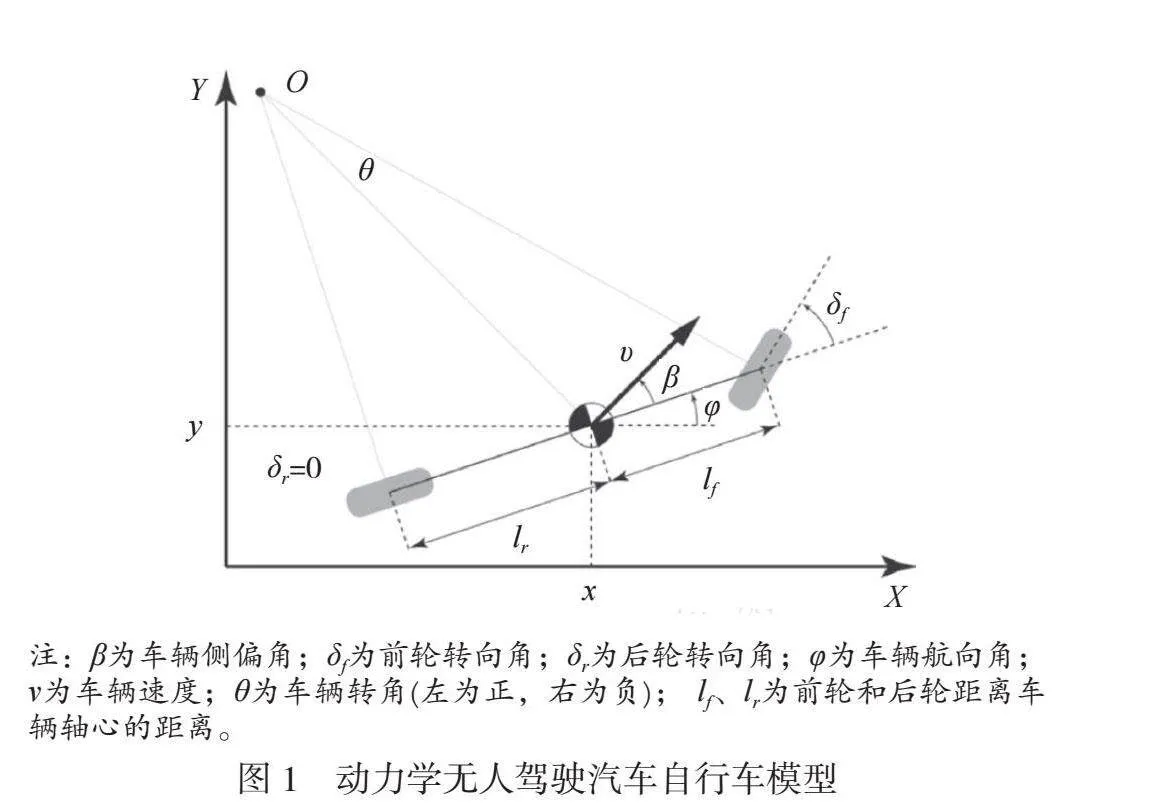
假设如下。1）车身悬架系统为刚性系统。2）车辆运动转向由前轮驱动。3）以后轴为运动原点。自行车模型如图1所示。

任意时刻车辆的状态用车辆运动学模型来表示，如公式

（1）～公式（3）所示。

=tanθ （1）

= （2）

tanθ=sinθ/cosθ （3）

式中：x、y分别为车辆在x轴、y轴移动的距离；θ为车辆转角。

一定约束下的单车模型速度运动学模型如公式（4）、公式（5）所示。

（4）

=a （5）

式中：v为车辆速度；L为前后轮间距；ϕ为车辆转向角；a为车辆加速度。

基于上述模型，可以估算车辆在下一时刻的状态信息，随后引入车辆的动力学特征。考虑车辆发动机的动力、轮胎和路面之间的相互作用以及真实汽车的转向能力，提高自动驾驶车辆建模的准确性，从而提升车辆运行的控制性能。由于无人驾驶汽车在高速行驶中车轮方向与实际运动速度方向不一致，因此引入车辆的动力学模型。

本文针对车辆横向动力学数学模型进行研究，包括轮胎横向力和转向控制系统，可以实现无人车的最优控制。该方法以数学模型为基础，在给定的约束条件下，通过优化算法计算最优控制策略，以实现无人车在行驶过程中的最佳性能。由于无人驾驶汽车在高速行驶中车轮方向与实际运动速度方向不一致，因此引入车辆的动力学模型。

模型中各状态量为、、、X和Y，如公式（6）～公式（10）所示。

=+ax （6）

=-+（Fc，f cosδf+Fc，r） （7）

=（lfFc，f-lrFc，r） （8）

=cosψ-sinψ （9）

=sinψ-cosψ （10）

式中：ax为x方向的加速度；ψ为偏航角度；（X，Y）为车身坐标；δf为前轮转向角；lf、lr为前轮和后轮距离车辆轴心的距离；m和Iz为车辆的质量和偏航惯性；Fc，f、Fc，r分别为前、后轮胎受到的侧向力。

2.2 无人车控制的约束条件

首先，车辆受到速度约束，为了保障驾驶安全并保证控制的稳定性，车辆的速度既不能超过最大值，也不能低于最小值。过高的速度可能导致车辆失控，而过低的速度可能会影响交通畅通和效率。

其次，车辆的转向能力受到物理限制，这是机械设计和道路条件对转向角度和速度的实际影响。为了避免车辆因转向角度过大而造成侧翻或其他危险情况，转向角度必须受到限制。车辆的加速能力和减速能力也要受到约束。过大的加速度或减速度（刹车力）不仅影响乘客的舒适度，而且在某些情况下可能是危险的，尤其是在湿滑的道路上。

最后，车辆受到物理环境约束。通过感知模块，实时监测和控制无人车辆。其计算过程如公式（11）～公式（13）所示。

vmin≤v≤vmax （11）

δmin≤δ≤δmax （12）

amin≤a≤amax （13）

约束条件在无人驾驶汽车的控制中起到了重要的作用，它保证车辆安全运行，还有助于优化车辆的性能并提高效率。当设计无人驾驶汽车的控制策略时，需要考虑并满足这些约束条件。

3 基于MPC的无人车辆控制器设计

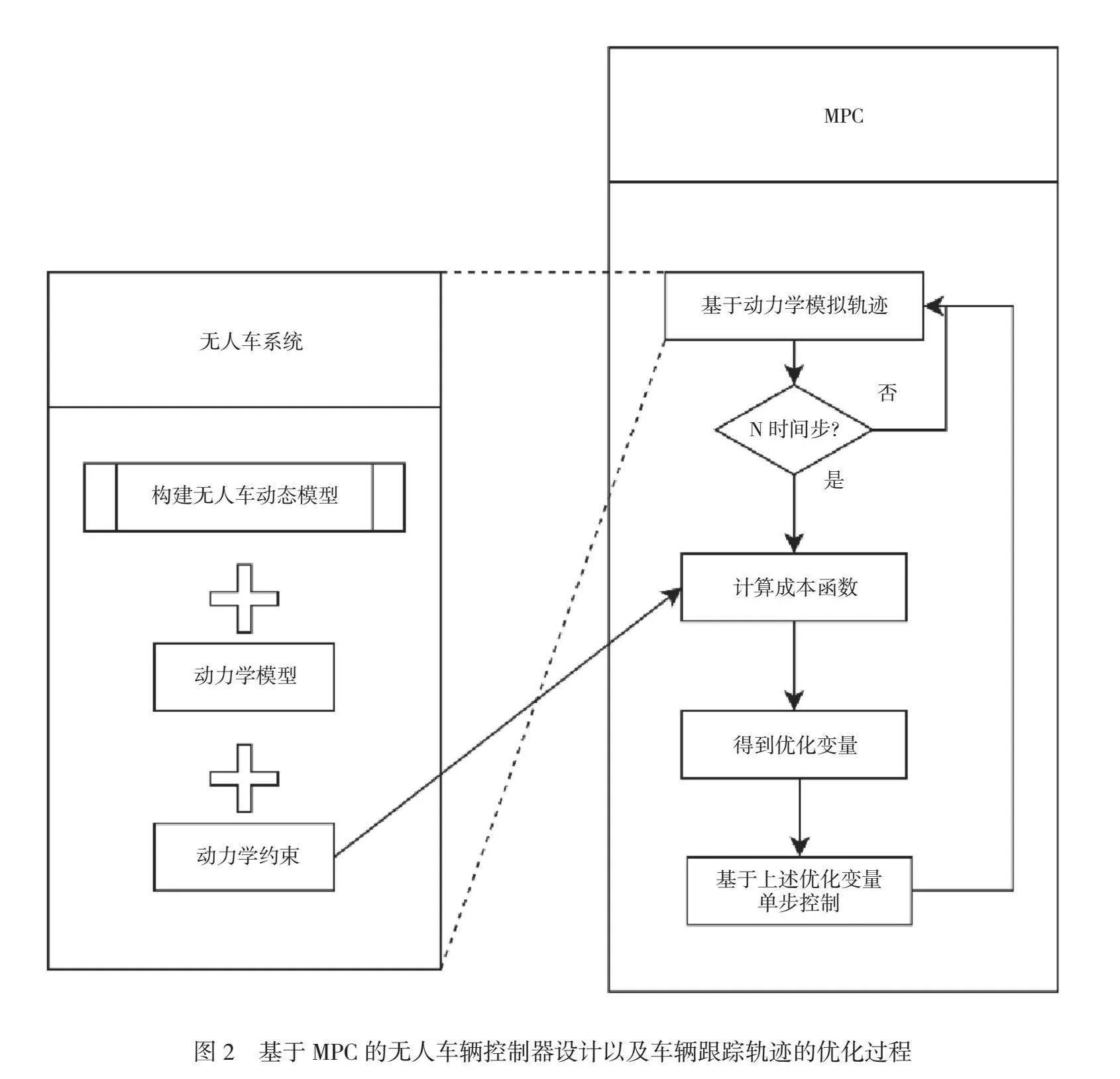
MPC是一种在线优化方法，它使用模型预测未来的系统输出，并基于这些预测来调整控制输入，以满足某些性能指标和约束条件。对无人驾驶汽车来说，MPC可以用来优化轨迹、加快速度并完成其他驾驶任务。本文将基于MPC实现无人驾驶汽车的控制系统设计，使用MPC在给定的时间窗口内优化无人驾驶汽车轨迹跟踪，并实现最大化速度，同时满足所有约束条件。

基于MPC的无人车辆控制器设计以及车辆跟踪轨迹的优化过程如图2所示。

定义系统的状态向量x和控制向量u，如公式（14）所示。

（14）

式中：对无人车辆来说，一个典型的状态向量包括位置xpos、ypos、速度v、车辆转角θ，控制向量包括油门uthrottle、刹车ubrake和转向usteer。

基于上述无人车数学模型，系统的动态如公式（15）所示。

x（t+1）=Ax（t）+Bu（t） （15）

式中：A、B为系统矩阵，描述了无人车的动力学特征；x为系统状态向量；t为时间步。

假设当前车辆的轨迹已经确定，MPC算法基于车辆的动态模型建立了一个离散的状态空间模型[4-5]，并利用该模型进行预测。通过预测车辆在未来一段时间（记为N）的控制向量u，可以生成一系列候选的控制指令序列。优化算法会遍历所有候选指令序列，并根据预先定义的性能指标对其进行评估。最终选择具有最佳性能的控制指令序列，以达到期望的轨迹跟踪效果。

基于上述动力学模型，可以从最新时刻采样数据推导下一时刻车身的位置和速度。设定一个时间窗口，N个时间步，MPC 将预测在这N个时间步内的系统行为。在此窗口内，目标是最小化一个成本函数J，该函数是关于预测的车辆的状态和控制输入的函数。另一个目标是尽可能地抑制加速、减速和转向变化率，包括跟踪误差、转向误差、速度损失函数项、转向损失函数项、加速度损失函数项、转向变化率和加速度变化率。具体计算过程如公式（16）所示。

（16）

式中：xref和uref为参考轨迹和控制输入；Q和R分别为对参考轨迹和控制偏差之间的权值分配矩阵；k为在第k时间步下。

公式（16）需要满足公式（11）～公式（13）的约束条件。本文采用SQP算法对该优化问题进行求解，解算时间步下的最小总损失，该算法将输出优化控制序列u*（0）…u*（N-1）用于控制车辆，基于上述损失函数，计算采样周期的损失函数。选择第一个周期时间步下的控制量u*（0），将该控制量传递给下位机并进行车辆电机和舵机控制，最后，向前移动一个时间步，考虑新的初始条件，重新解决该优化问题。

4 试验设计与结果验证

本文在Ubuntu系统中的CARLA无人驾驶车辆仿真平台上进行仿真试验，以验证本文设计的基于模型预测的无人车辆控制方法的效果。在仿真平台中为车辆速度设定一个目标轨迹，该轨迹由一系列离散点组成，车辆的任务是跟踪这个轨迹，并尽量避免碰撞。车辆物理模型使用该仿真系统的默认值，对车辆轨迹跟踪算法进行替换，针对不同道路轨迹平均曲率下的轨迹跟踪效果，验证本文采用的MPC控制器的适应能力。

评价指标采用轨迹偏差（Bias），碰撞次数和完成时间作为评价控制性能的指标，如公式（17）所示。

（17）

式中：xi、yi分别为车辆在第i个时间步的位置；xref、yref分别为目标轨迹的对应点；N为跟踪样本点个数。

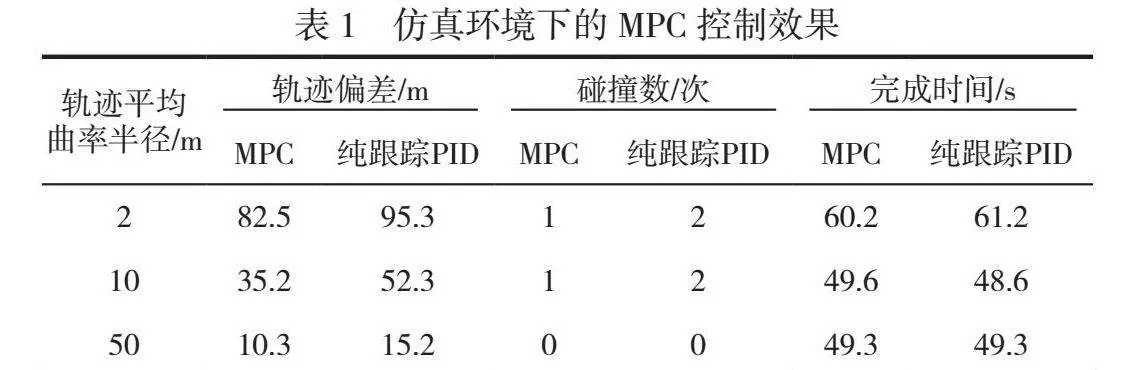
仿真环境下的 MPC 控制效果见表1。

从上述结果可以看出，本文提出的基于模型预测控制的无人驾驶车辆轨迹跟踪控制与经典的纯跟踪和PID控制器算法相比，具有一定优势，在轨迹偏差评价指标中误差更小，控制效果更好。由于更贴合仿真轨迹，因此障碍物碰撞次数也相对较少，安全隐患低。从完成轨迹跟踪耗时的角度来看，MPC控制的无人车完成时间更短，整体速度更快，更能满足车辆行驶的速度要求。在小曲率半径下，MPC控制会取得明显优于纯跟踪和PID控制器算法的效果，这进一步表明该算法的控制效果当面对更困难的任务时会有良好的应用前景。

5 结语

无人驾驶技术的快速发展为现代交通带来了新的机遇和挑战，该技术不仅可以减轻驾驶员的负担，提升出行的舒适度和安全性，还能有效节省能源和环境资源。基于动力学模型和模型预测控制算法，本文设计了一种轨迹跟踪控制方法。通过试验验证，本文提出的基于MPC的无人车辆最优控制可以在复杂工况和各种速度的情况下保证系统的准确性和稳定性，进一步优化无人驾驶系统的控制性能。

参考文献

[1]王治国，郑泽东，李永东，等.交流电机模型预测控制综述[J].电机与控制学报，2022，26（11）：14-30.

[2]赵超轮，戴邵武，赵国荣，等.基于分布式模型预测控制的无人机编队控制[J].控制与决策，2022，37（7）：1763-1771.

[3]曾望云，隗寒冰.基于车辆动力学模型的换道轨迹规划研究[J].汽车工程学报，2022（126）： 815-824.

[4]白世超.基于模型预测控制的智能车辆轨迹跟踪方法研究[D].哈尔滨：哈尔滨理工大学，2021.

[5]庞辉，刘楠，刘敏豪，等.基于线性时变模型预测控制的自主车辆轨迹跟踪控制器设计与验证[J].机械工程学报，2022，58（24）：264-274.