关注情境意义 经历建模过程
2024-12-04陶品


【摘 要】混合运算是小学阶段数学学习的重要内容之一。在教学中,学生应在理解情境的基础上,用合适的方式表征情境并列出综合算式,这实际上就是在用数学的语言描述情境中的两个或两个以上的故事,建立模型并求解模型的过程。以北师大第四版教材三年级上册“乘加混合运算”为例,确定“混合运算”单元模型意识的具体表现,构建“乘加混合运算”课时表现性目标与任务设计,来进行教学实施。
【关键词】模型意识;混合运算;情境意义;表现性任务
“混合运算”是北师大第四版教材三年级上册第一单元的学习内容。该单元采用“问题情境—建立模型—解释与应用”的叙述方式,通过“小熊购物”“买文具”“过河”等现实情境,生动呈现了多种混合运算的实际应用模型。学生需深入理解这些情境,运用合适的方式表征情境并列出综合算式,这一过程本质上是在用数学的语言描述情境中的两个或两个以上的故事,进而建立模型并求解模型。
在实际的教学中,如何有效引导学生对情境、表征与数学符号进行关联,从而在混合运算的学习中发展模型意识?本文以北师大第四版教材三年级上册“乘加混合运算”为例,确定本单元模型意识维度和具体的表现性水平层次,从而实现具体课时的任务设计与实施过程。
一、学习目标确立与教学任务设计
该单元聚焦于混合运算的教学,其涵盖的运算涉及多个基本运算的并列关系或含有先后顺序的多级运算。在本质上,这些运算应当分步进行计算,但若想要用一个综合算式表示,就形成了混合运算。为确保混合运算的结果与分步计算的结果一致,需要明确现实情境中事件的顺序,即哪些事件是先发生的,哪些事件是后发生的,据此构建综合算式,并确保综合算式中的运算顺序与现实情境保持一致。
在这一过程中,关键在于培养学生解读现实生活情境、理解信息、识别关系的能力,从而确立事件发生的先后顺序,以此来确定运算顺序。此外,学生还需学会将信息进行表征,并用算式进行表达,逐步领悟小括号的意义,明确小括号可以用来表示先算部分的作用,并加以灵活运用。模型意识在本单元的具体表现如表1所示。
基于上述模型意识在该单元的具体表现,可构建“混合运算”单元中的“乘加混合运算”课时表现性目标与任务设计(如表2)。
二、表现性任务的实施
(一)自主购物,独立表征信息
教师设计了学生熟悉的自主购物情境图,情境图中提供丰富多样的购物信息,使学生能够从中自主选择并提出与加、减、乘、除相关的实际问题。通过教师提问,引导学生从购物情境出发,理解信息、识别关系并尝试对信息进行表征。
【教学片段1】
教师出示购物情境图(如图1)。
任务一:想一想,你想购买哪些物品?用简单的图画表示出来。
学生自主活动后进行全班交流,教师呈现学生作品1(图略)。
师:大家知道这个同学想买什么吗?
生:他想买2个蛋糕和3个面包。
师:你们是怎么看出来的?
生:他画了2个蛋糕和3个面包,一看就知道了。
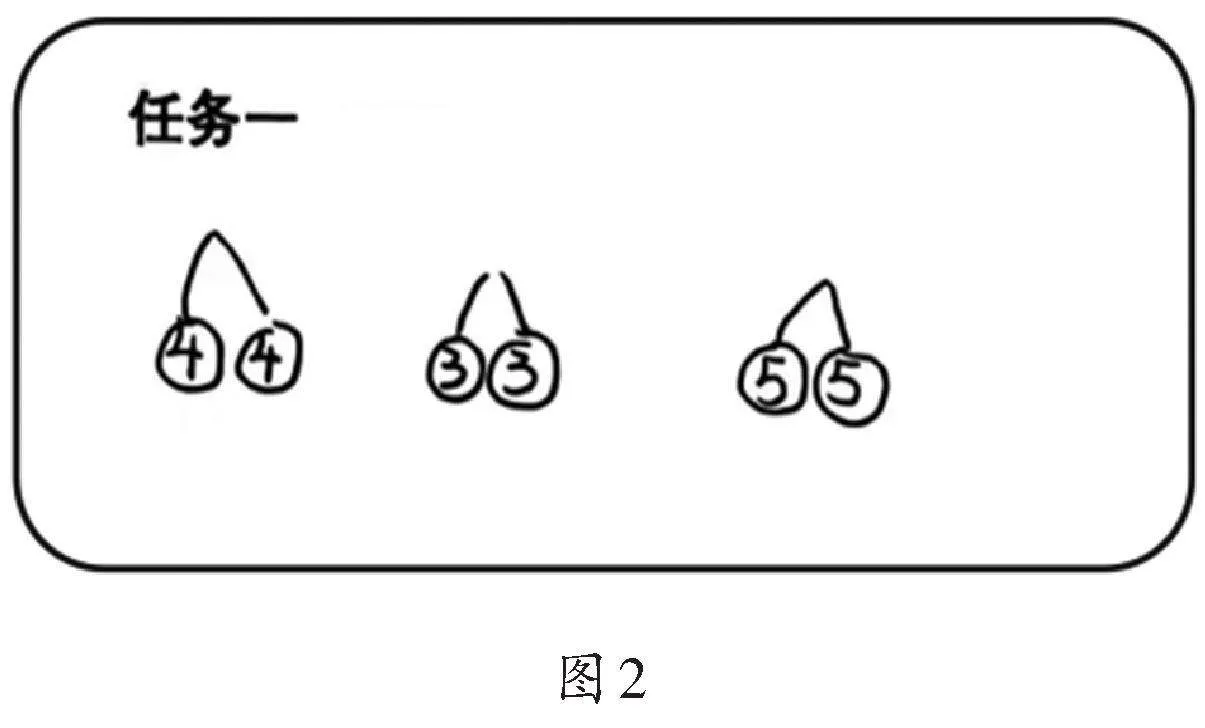
教师呈现学生作品2,如图2所示。
师:那这位同学想买什么呢?
生:他想买2包饼干,2个面包,还有2袋糖果。
师:你是怎么看出来的?
生:他虽然没有画出商品的样子,也没有写名称,但是他写出了价格,我们也能看出是什么物品。
师:看来只要画出关键信息,就能把故事讲清楚。
设计意图:鉴于学生第一次接触此类情境图,本环节教学进度较为缓慢,旨在鼓励学生自主选择想购买的商品,并进行初步的表征。在教学过程中,教师对学生的购物图进行对比分析,采用叠加呈现的方式,引导学生深入讨论如何表达自己所想购买的商品。此过程旨在帮助学生感受到不同个体在表征同一事物时的差异性,并进一步体会将现实情境抽象为数学模型的全过程。
(二)理解情境,呈现多元表征
通过一个生动的“胖胖的购物故事”,引导学生对情境中信息的理解进行多元表征。利用小组间讨论和教学反馈,实现学生对不同表征方式的认识。
【教学片段二】
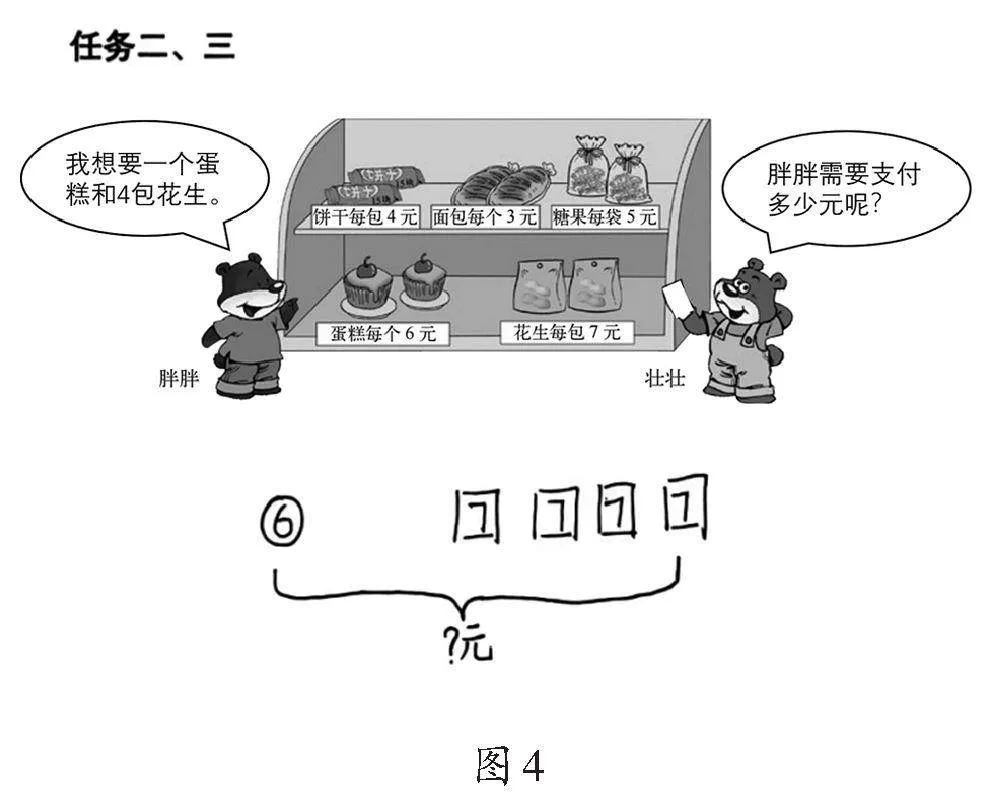
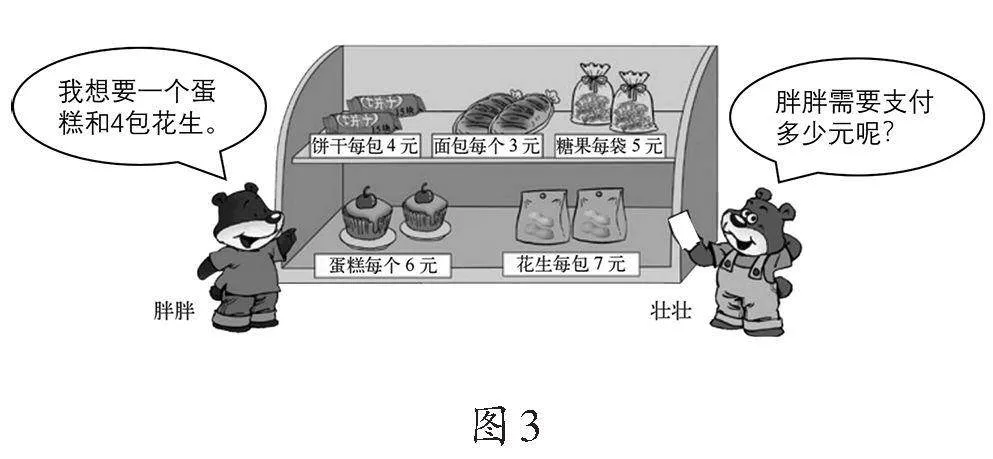
教师出示胖胖的购物情境图(如图3)。
活动要求。
(1)圈一圈:圈出情境中的关键信息。
(2)画一画:画出胖胖的购物故事。
(3)看一看:小组交流,你能看懂小组内其他人画的购物图吗?
学生根据活动要求独立完成,教师呈现学生作品3(图略)。
师:大家能看懂这个同学画的购物图吗?
生:他画了4包花生和1个蛋糕,就是说胖胖要买这些商品。
教师呈现学生作品4,如图4所示。
师:那这个同学的图呢?他画出胖胖想买的东西了吗?
生:他圆圈里写6,表示1个蛋糕的价格,长方形里写7,表示每包花生的价格,也表示出了胖胖想买的商品。
师:那下面的大括号和问号是什么意思?
生:就是问买这些东西一共需要花多少元?
设计意图:本环节引入了胖胖的购物故事,旨在促使学生对这一情境进行深入理解与分析。学生需明确胖胖的购物故事中包含了两个独立的购物线索,并具备准确判断这两个线索发生先后顺序的能力。此环节为后续进行列式计算奠定了坚实的基础。
(三)列式计算,综合基本模型
学生在现实情境中对信息的理解与多元表征的基础上,提取了几个基本模型,并结合情境中事件发生的先后顺序,以此合成综合模型,列出相应的算式。
【教学片段三】
活动要求。
(1)根据提供的购物图,列式计算胖胖需要支付的金额。
(2)在小组内,说一说所列算式的具体含义。
教师根据学生回答列式:4×7=28(元),28+6=34(元)。
师:大家能看懂这个算式吗?
生:4×7表示胖胖要买4包花生,即要花4×7=28(元),因为还要加上1个蛋糕的钱,所以28+6表示胖胖需要支付的金额。
师:这个同学发现胖胖的购物图里包含了两个购物信息,要计算其总金额。他先计算4包花生的金额,再加上1个蛋糕的金额。大家想一想,能不能把这两个算式合并成一个综合算式?
教师出示一名学生列的综合算式:4×7+6=34(元)。
师:你是怎么想的?
生:根据购物图和题目呈现的问题,我先算4包花生的金额,再加上1个蛋糕的金额。
师:说得真好,能结合你的综合算式说明一下吗?
生:先算4包花生的金额,就是先算4×7,再加上1个蛋糕的金额,就是再加6。
教师出示另一名学生列的综合算式:6+4×7=34(元)。
师:你是怎么想的?
生:我是先算4包花生的金额,再加上1个蛋糕的金额。
生:他的意思是对的,但算式好像不对,容易让人误以为是先算6+4。
师:在这个购物故事里,要先算什么?
生:4×7。
师:有没有办法,能让所有人都知道先算4×7?
生:用小括号把4×7括起来,让大家知道要先算这个。
设计意图:本环节引导学生聚焦于综合算式的运算顺序探讨。值得注意的是,尽管算式6+4×7在不加小括号的情况下,其计算结果与现实情境相对应,但这是在学生已掌握“先算乘除法,再算加减法”运算法则的前提下。因此,当学生面对该算式的运算顺序产生困惑时,可适时引用“利用小括号来表示先算的部分”来解释。
【教学片段四】
活动要求。
(1)请你分享一个类似的购物故事。
(2)画一画:将你的购物图画出来。
(3)算一算:用综合算式计算结果。
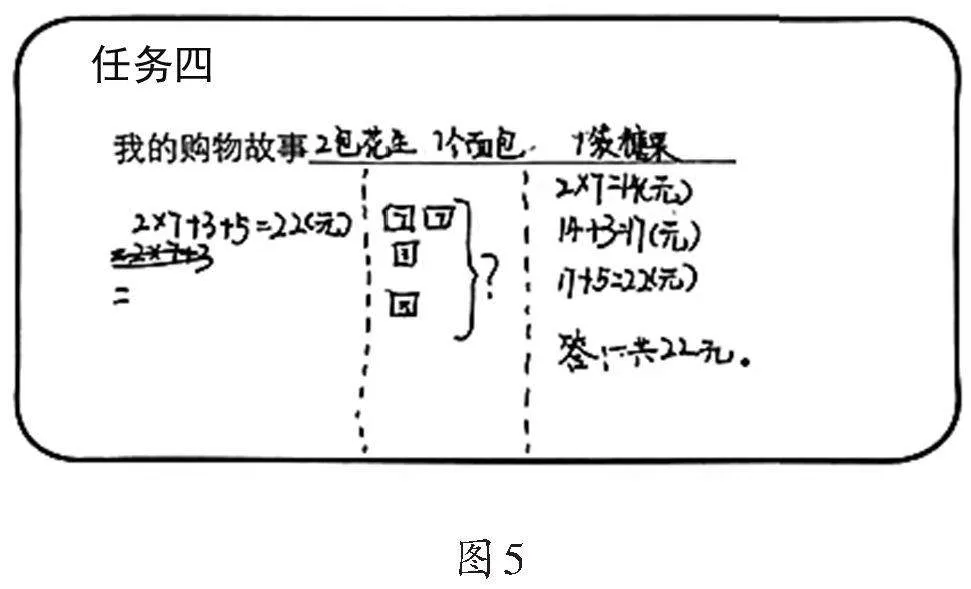
学生根据活动要求独立完成,教师呈现学生作品5,如图5所示。
师:请这个同学来分享一下他的购物故事。
生:我想买2包花生、1个面包和1袋糖果。要先计算2包花生的金额,再分别加上1个面包和1袋糖果的金额。因此,我列出的算式为7×2+3+5。
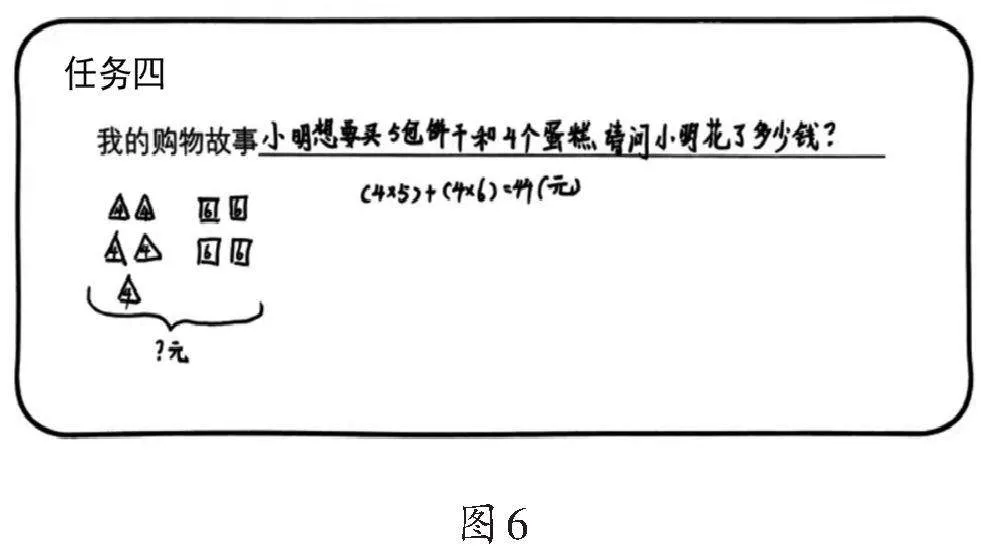
教师呈现学生作品6,如图6所示。
师:请这个同学也来分享一下他的购物故事。
生:我想买5包饼干和4个蛋糕,我先分别算出5包饼干和4个蛋糕的金额,为了保证4×5和4×6先算,我给它们都加上了小括号。
师:你们的讲解很精彩,都考虑到了运算顺序的问题。
设计意图:通过前述几个活动,学生已经经历了理解情境、表征信息与问题的过程,对综合乘、加两种基本运算的模型有了丰富的认识。因此,在此活动过程中,学生能够自然地自主提出涉及乘加混合运算的问题,并借助表征图,从中抽象出多个基本运算模型,进而综合这些基本模型,列出相应的综合算式。
三、教学思考
(一)深化理解,讲好情境故事
在“混合运算”单元的学习中,学生常忽略对现实情境的理解,仅追求按照规定的运算顺序快速计算结果。当情境较复杂时,他们往往难以厘清运算顺序。究其原因,这源于学生未能明确问题中包含了几个故事及这几个故事发生的先后顺序,更难以用算式准确表达复杂情境。因此,本节课着重通过讲故事的方式,引导学生多角度、反复地表达情境故事,从而在学生表达过程中发现情境包含的多个故事,明确这些故事发生的先后顺序,为正确列出算式并按运算法则进行计算奠定基础。
(二)多元表征,强化数学关联
在问题情境转化为数学模型的过程中,学生需经历数学抽象。其中,对情境中信息的表征显得至关重要。面对同一情境,不同的学生会呈现不同的表征。教师应有序呈现从具体到抽象的多元表征,让学生感受“数学化”与“抽象化”的过程。在这一过程中,教师应鼓励学生基于表征,尝试用符号表达情境中的数学关系。学生在分步列算式时,需要依托表征,挖掘情境中包含的多个故事,从中提取乘法和加法的基本模型,并列出对应的算式。学生在列综合算式时,也需要依托表征,明确情境中多个故事发生的先后顺序,将乘法和加法的基本模型合并成乘加的复杂模型,并将多步算式合并成综合算式。
(三)拓展迁移,感悟模型价值
迁移、拓展和重复使用数学模型是数学模型建立的核心活动,在教学中,除了深入研究教材提供的购物故事外,还应引导学生自主设计有关乘加混合运算的问题。学生在自主设计相应问题的过程中,自然会对这节课经历的整个建模过程进行反思,将乘加模型进行解构、重组并产生新的理解。在交流、解读其他同学设计的问题中,不断重复应用、解释乘加数学模型,强化对乘加模型的理解与应用,感受乘加模型可以解决一类问题。
参考文献:
[1]中华人民共和国教育部.义务教育数学课程标准(2022年版)[M].北京:北京师范大学出版社,2022.
[2]章勤琼,阳海林,陈肖颖.小学数学教学中的表现性评价及其应用[J].课程·教材·教法,2021,41(3):83-89.
