早期儿童空间能力干预能提升数学能力吗？

［摘 要］ 空间能力与数学能力紧密相关，但空间能力干预能否提升早期儿童的数学能力尚不明晰。为进一步明确空间能力干预对早期儿童数学能力的影响，本研究采用元分析方法对24篇国内外相关研究进行整合分析。结果发现，已有研究能够证明空间能力干预可以提升早期儿童的数学能力，儿童年龄、干预方式、文化背景是影响干预效果的重要因素，而空间能力维度和干预总时长不影响干预效果。建议教育者抓住早期儿童数学能力发展的关键期，创设有利于儿童空间—数字联合表征的环境；丰富早期儿童的具身空间体验，通过多样化的活动支持儿童的数学学习；发挥空间思维在数学学习中的作用，鼓励早期儿童运用空间策略解决数学问题。

［关键词］ 空间能力；数学能力；元分析

一、问题提出

儿童早期数学能力是其未来数学、语言等多领域学术成就的重要预测因子。[1]探究早期儿童数学能力发展的影响因素，可以更好地揭示个体数学能力的发展特点，帮助教育工作者更好地理解儿童早期的数学学习，引导儿童做好数学的入学准备和入学适应。当前，学者们对数学能力的定义尚不一致。全美数学教师协会将儿童的数学能力划分为内容性数学能力和过程性数学能力。[2]国内学者认为数学能力是个体有效完成数学活动的心理特征，[3]主要由三种基本数学能力（数学运算能力、逻辑思维能力和空间想象能力）和五种数学思维品质（思维的深刻性、灵活性、独创性、批判性和敏捷性）构成。[4]也有学者将数学能力划分为数量能力、计算能力、几何能力和逻辑思维能力，[5]其中前三项能力是在不同的脑区中被激活且相互独立的，逻辑思维能力则是对数学规则和数量关系进行分析和整合的能力。[6]总体而言，数学能力的各组成部分之间相互依存、相互制约，共同构成了动态、多层次和多维度的立体网络结构。[7]在本研究中，早期儿童数学能力是指个体有效完成数学活动的个性心理特征，即个体在运用数学知识解决数学问题活动中形成和发展起来的心理能力。

空间能力是个体感知、分析和理解物体形状、位置、运动轨迹以及物体间关系的能力，[8]是影响个体数学能力发展的重要因素。国内外学者对空间能力的界定有两种。一种是基于语言学和神经科学把空间能力分为内部、外部和静态、动态两大维度，两大维度交叉后得到四种空间能力：内部—动态空间能力、内部—静态空间能力、外部—动态空间能力和外部—静态空间能力。[9]另一种是基于因素分析法，从主体理解空间关系及在心理上对表象进行操作的维度来进行界定。国际上较认可的是林（Linn）和彼得森（Petersen）提出的空间能力三因素结构说，即空间知觉、心理旋转和空间视觉化。[10]其中，空间知觉能力是个体理解空间中不同位置关系的能力，心理旋转是指个体对二维或三维图形表征的转换能力，空间视觉化是个体在头脑中形成的对物体表象的认识并用翻转等操作表现出来的能力。空间能力有助于个体在心中形成和操作几何图形，从而更好地解决几何问题。因此，空间能力被认为是理解和应用数学尤其是几何知识的重要基础。本研究认为空间能力是一种基础性认知能力，因此采用三因素结构说这一定义。

空间能力和数学能力关系密切。纵向研究表明，即使在控制了儿童的年龄、语言能力和家庭社会经济地位等变量后，大班时期的空间能力与其二年级的数学成绩呈正相关，且空间能力能预测数学成绩。[11]空间能力与数学能力是如何关联起来的呢？空间—数字编码联合效应（sDlJSTKnD7M4pk2044cT5lA==patial⁃numerical association of response codes effect， SNARC）为其提供了一种解释。[12]这一效应指出了数字心理空间表征的特点，即人们在心理上倾向于把数字表征为一条从左到右的“心理数字线”，数字线将空间与数学认知联系起来，帮助儿童理解数字的顺序、大小等关系。脑科学研究进一步揭示了空间与数学之间的关系。脑成像的研究发现，人们在加工空间和数字信息时激活了部分相同的脑区。[13]例如，数量表征的神经环路定位在顶叶和额叶，而这两个区域与空间表征的神经环路存在部分重叠。[14]

为了进一步探究两者的关系，越来越多的研究者开始关注空间能力干预能否对早期儿童数学能力的发展产生影响。以往研究主要有三种不同的观点。第一种观点认为，对儿童进行空间能力干预不仅可以增强空间思维的神经功能，[15]甚至能迁移到儿童的整体数学能力。例如，有研究者对5～6岁儿童进行心理旋转能力干预后发现，儿童的空间能力和数学能力都得到了明显提高。[16]第二种观点认为，某一空间能力的干预只能影响特定的空间能力和数学能力，而不会对全部的数学任务产生影响。亚当斯（Adams）等学者对儿童的空间推理技能进行了干预，发现他们的几何能力得到了提高，但计算能力和数量能力并未得到改善。[17]第三种观点认为，空间能力干预能够提高儿童的空间能力，但不能迁移到数学能力上去。霍伊斯（Hawes）等学者发现，接受干预和未经干预的儿童只在空间任务上的表现有明显差异，表明干预能提高儿童的空间能力，但不能提高儿童的数学能力。[18]

产生上述分歧的原因可能有以下五个方面。第一，儿童年龄可能会调节空间能力对数学能力发展的影响。有研究指出，空间能力与数学能力的关系会随着儿童年龄的变化而改变。[19]在儿童发展早期，空间思维的加工过程与数学能力的关联可能更为紧密。[20]有研究发现，对学前儿童进行空间能力干预可以提高其数学能力，[21]但对小学生进行空间干预并不能提高他们的数学成绩。[22]第二，干预方式可能会调节空间能力对儿童数学能力发展的影响。儿童早期抽象逻辑思维还处于萌芽状态，理解数量与空间的关系常常需要依赖具体的实物或者手部动作。虽然基于电子游戏和实物操作的干预都能提升儿童的空间能力，[23][24]但只有使用实物操作才能提高儿童的数学能力。第三，空间能力干预的时长也可能影响干预效果。理论上说，更长时间的空间能力干预更能影响儿童数学能力的发展，但以往研究并没有证实这一观点。有研究发现，对儿童进行6周的干预，儿童数学成绩的提升水平却与40分钟的干预效果相差不大。第四，空间能力存在多个维度，干预其中某一维度或某几个维度可能会对儿童数学能力产生不同的影响。例如，对空间知觉的干预能够有效提高儿童的数学能力，[25]对心理旋转的干预则不能提高儿童的数学能力。[26]第五，文化背景可能会对空间能力与数学能力之间的关系产生影响。文化维度理论构建了衡量不同国家文化差异的框架，在“长期取向与短期取向”这一维度（Long⁃Term Versus Short⁃Term），长期取向的文化注重未来，短期取向的文化重视当下。[27]西方文化以短期取向为主，认为学生应该在学习过程中体验快乐。而东方文化以长期取向为主，认为学习应该与艰苦劳动相伴，只有艰苦劳动有结果才能获得真正的快乐和满足。因此，东方文化更注重儿童的学业成就，通过投入大量的时间和金钱来规避未来的不确定性。[28]

鉴于元分析的方法可以对以往多项研究成果进行整合分析，避免了单一研究的测量误差，因此有必要运用元分析方法深入探讨空间能力干预对早期儿童数学能力发展的影响，并分析影响干预效果的可能因素。已有学者采用了元分析的方法探究空间能力干预对早期儿童数学能力发展的影响，[29]推动了空间能力与数学能力关系理论的发展。但以往研究多聚焦学龄儿童和西方儿童，忽视了对年龄和文化因素的考察。学前儿童与学龄儿童的思维特点与学习方式存在差异，0～8岁是儿童空间能力迅速发展的时期，[30]早期干预可能比后期干预更有效。[31]因此，空间能力干预是否可以提高早期儿童的数学能力，以及如何将其应用到学前儿童的入学准备和入学适应中去还值得研究。此外，文化背景也能够影响儿童数学能力的发展。[32]关于西方儿童空间能力干预的元分析结果并不能直接运用到东方文化情境之中，因而有必要对东西方文化背景下的干预研究进行比较，从而为我国早期儿童空间以及数学能力的发展提供更可靠、更稳健的参考依据。

二、研究方法

（一）文献检索

在英文数据库Web of Science、Pubmed、EBSCOhost中，使用关键词组合“child/student/kindergarten/primary school”“training/practice/experience”“spatial/mental rotation/scaling/visualization skills”“mathematics/maths/mathematical/numeracy/arithmetic/calculation/geometry”进行检索。同时在中国知网、万方、维普和中国硕士学位论文全文数据库中，使用关键词组合“训练/练习/干预”“心理旋转/空间可视化/空间知觉/空间能力/空间技能”“数学能力/数学技能/运算/几何/推理”“儿童/幼儿/幼儿园/小学”进行检索。最初的检索标准包括：文献中呈现量化研究的数据结果，研究内容聚焦空间能力干预对数学能力的影响。鉴于儿童早期是空间能力干预的关键阶段，本研究将年龄范围聚焦于0～8岁。

（二）文献纳入标准

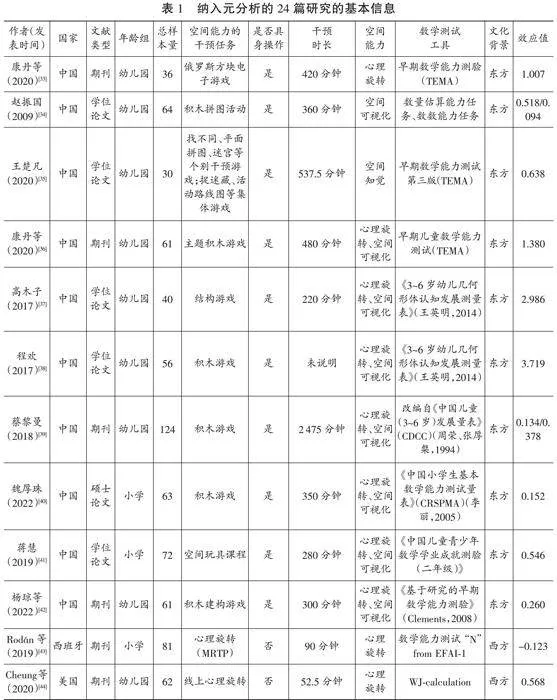
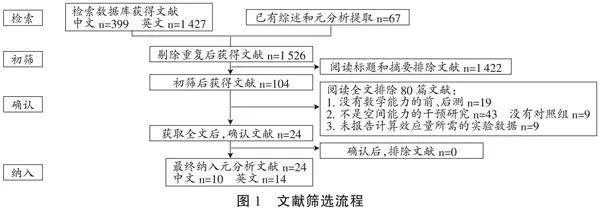
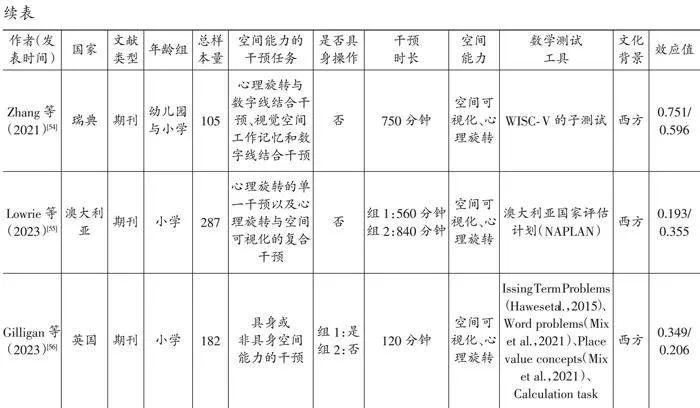
对于检索到的文献，文献纳入的标准为：（1）研究类型为随机对照实验或准实验设计，实验组为空间能力的干预组，对照组为没有干预任务或者干预非空间能力的任务；（2）干预对象为0～8岁儿童；（3）对干预方案有详细且清晰的介绍；（4）利用数学任务对儿童干预前后的变化进行评估，且不同组别的评估方式统一；（5）样本量不低于10人；（6）文献形式包括但不限于学术期刊文章、专著章节、会议论文、学位论文；（7）文献语种限制为中文或英文；（8）文献发表时间区间为 2000年1月1日至2024年1月30日。最终纳入24篇文献，共45个独立研究。文献筛选流程见图1。

（三）文献编码

详细阅读和编码每一篇纳入元分析的文献，包括以下信息：（1）出版特征：出版年份；（2）样本特征：被试人数、被试年龄；（3）干预特征：干预时长、操作方式；（4）空间能力的干预维度：空间知觉、心理旋转、空间视觉化；（5）文化背景：东方文化和西方文化。对每一个独立样本，计算得到一个效应量，如果一篇文献中包含多个独立样本，则相应地进行多次编码，产生多个独立效应量。

本研究元分析的编码工作由两位编码者完成，编码者一致性为92.5%，说明本研究的文献编码较为有效和准确。两位编码者讨论了所有存在分歧的地方，最终达成一致。本研究纳入元分析的文献共24篇，共计45个独立效应量。

（四）效应值计算

本研究将实验组和对照组儿童数学能力变化的均值差作为效应量。计算效应量时考虑了干预前测的数据，先分别计算两组的前后测变化量，再计算两组之间变化量的差异。由于干预研究的样本量较小、不同研究的实验设计和测查工具存在差异，因此本研究采用标准化的均值差 Hedges’s g作为效应值。当0.2≤g<0.5时，认为效应量较小；当0.5≤g<0.8时，属于中等效应；当g≥0.8，认为效应量较大。[57]

（五）数据分析

本研究运用CMA 3.0（Comprehensive Meta Analysis 3.0）软件进行数据处理。首先，采用异质性Q检验和I2检验考察效应值间的异质性，基于此选择分析模型。目前元分析一般采用固定效应模型（fixed effect model）和随机效应模型（random effect model）。固定效应模型假定所有研究的真实效应量相同，研究结果间的差别由随机误差导致；随机效应模型认为不同研究的真实效应量可以不同，除受随机误差外，还会因研究群体和研究工具的不同而有所不同。[58]本研究在梳理文献后发现，空间能力的干预对数学能力的影响可能受被试年龄、干预的空间能力维度、干预时长、是否具身操作等因素的调节。因此，本研究采用随机效应模型进行元分析，并通过异质性检验（Heterogeneity Test）进一步验证随机效应模型选择的合理性。其次，检测出版偏倚。出版偏倚（publication bias）意味着发表的研究文献不能系统全面地代表该领域已经完成的研究总体。[59]出版偏倚会影响元分析的可靠性，在具体的元分析过程中，本研究采用漏斗图和失安全系数来评估出版偏倚。最后，本研究采取选定模型检验主效应，即空间能力的干预对儿童数学能力的影响，采用亚组分析和元回归检验年龄、文化背景、不同干预特征对二者关系的调节效应。

三、研究结果

（一）异质性检验

采用Q检验和I2检验评估纳入元分析的各项研究结果的差异性。[60]Q值越大，p值越小，说明纳入研究的异质性越大。I2值反映了异质性部分在效应量中总的变异中所占的比重。一般认为，p<0.05或者I2>50%表明研究间存在显著的异质性。本研究运用CMA 3.0软件进行异质性检验，结果见表2。Q值为166.185（p<0.01），I2值为73.52%，表明文献之间存在显著的异质性，在计算效应量时应采用随机效应模型进行元分析。[61]

（二）出版偏倚检验

从漏斗图（图 2）可以看出，已有研究基本集中在漏斗图中上方，处于漏斗图下方的研究较少。研究均匀分布在漏斗图两侧，基本上呈对称分布，这表明元分析存在出版偏倚的可能性较小。因漏斗图的评判存在一定的主观性，因此采用失安全系数（Classic Fail⁃safe N）来检验出版偏倚，定量估计p= 0.05时的出版偏倚水平。参考罗斯坦（Rothstein）等学者的研究，[62]采用5K+10（K表示研究数）作为临界值进行判断。结果显示，失安全系数为983，远大于临界值，表明本元分析存在发表偏倚的可能性较小。（见表2）

（三）主效应检验

本研究元分析包含24项研究和45个独立效应量，合计2 341名被试。通过CMA 3.0进行随机效应模型分析，结果显示空间能力干预对数学能力的影响为0.319（95%CI为[0.197～0.441]，p<0.001），说明空间能力干预能在一定程度上提高早期儿童的数学能力。

（四）调节效应检验

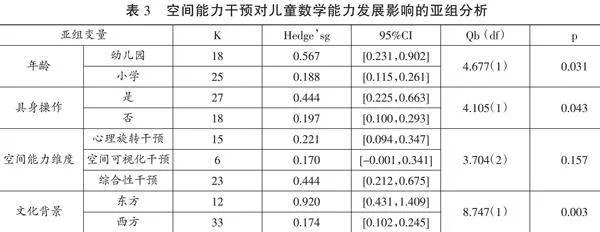
本研究采用亚组分析检验被试年龄、具身操作、空间能力干预维度、文化背景的调节效应，采用元回归分析检验干预时长的调节效应。

1. 被试年龄。

本研究根据各独立研究中儿童所在的学段进行分组，分为幼儿园和小学两组。亚组分析发现，学段对空间能力的干预对数学能力影响的调节效应显著（p=0.031）。幼儿园阶段儿童空间能力干预对数学能力影响的效应量为0.567（K=18），95%CI为[0.231，0.902]；小学阶段儿童空间能力干预对其数学能力影响的效应量为0.188（K=25），95%CI为[0.115，0.261]，相较于小学生，学前儿童组的效应值更大。

2. 具身操作。

本研究根据空间能力干预方法是否存在身体参与，将研究对象分为具身操作组和非具身操作组。亚组分析发现，具身操作能够调节空间能力干预对儿童数学能力发展的影响（p=0.043）。具身操作对儿童数学能力影响的效应量是0.444（K=27），95%CI为[0.225，0.663]；非具身操作对儿童数学能力发展影响的效应量是0.197（K=18），95%CI为[0.100，0.293]。相比之下，具身操作更能促进早期儿童数学能力的发展。

3. 空间能力的维度。

本研究以空间能力的子维度为划分依据，将干预分为心理旋转干预、空间可视化干预、空间知觉干预以及综合性干预（任意几种干预的组合）四组。由于空间知觉干预组的独立效应值不足4项（K=1），故不纳入此次亚组分析。亚组分析发现，空间能力的维度并不能调节空间能力干预对儿童数学能力发展的影响（p=0.157）。其中心理旋转干预对儿童数学能力影响的效应量是0.221（K=15），95%CI为[0.094，0.347]，空间可视化干预对儿童数学能力影响的效应量是0.170（K=6），95%CI为[-0.001，0.341]，综合性干预对儿童数学能力影响的效应量是0.444（K=23），95%CI为[0.212，0.675]。

4. 文化背景。

本研究以儿童所在的社会文化背景为划分依据，分为东方文化和西方文化两组。亚组分析发现，文化背景能够显著调节空间能力干预对儿童数学能力发展的影响（p=0.003）。东方文化背景下，空间能力干预对儿童数学能力影响的效应量是0.920（K=12），95%CI为[0.431，1.409]；西方文化背景下，空间能力干预对儿童数学能力影响的效应量是0.174（K=33），95%CI为[0.102，0.245]。可见，相比西方文化，东方文化背景下的空间能力干预对儿童数学能力发展的影响更大。

5. 干预时长。

本研究对干预时长进行元回归分析。结果发现，干预时长对儿童数学能力影响的调节效应不显著（b=0.0001，95%CI为[-0.0001，0.0002]，p=0.298）。

四、讨论

（一）空间能力干预能够有效提升早期儿童的数学能力

为进一步厘清早期儿童空间能力干预与其数学能力提升之间是否存在着因果关系，本研究采用元分析对现有研究结论进行了量化统计，共纳入了24篇文献，45个独立研究，样本总量为2 341人。对多项研究结果进行合并、计算后证明，空间能力干预在整体上对早期儿童的数学能力具有正向的影响（g=0.319），而且相比以往聚焦学龄儿童的元分析研究结果（g=0.28），[63]本研究的效应值更大。

空间能力干预能有效促进儿童数学能力的提高，这与已有的研究结果一致。[64]首先，空间能力与数学能力存在着密切的内在关联。一方面，根据空间—数字的反应编码联合效应（即SNARC效应），数字的心理表征是基于空间编码的，儿童在对抽象的数字进行加工时能够自动激活它的空间表征，[65]然后将空间表征映射在心理数字线上相应的空间位置，数字的空间表征为空间与数学之间的联系搭建了桥梁。另一方面，脑科学研究从生理机制的角度解释了这种内在关联，即与空间能力和数学能力认知机制相关的脑区存在部分重叠，它们使用类似的神经运算。儿童在运用空间思维的时候，可能激活了顶内沟等与数字和空间认知相关的共享神经机制，[66]并通过改变儿童原有的神经网络结构，对儿童的空间能力与数学能力同时产生影响。[67]

其次，空间能力的发展能够帮助儿童更加熟练地运用丰富的空间策略去解决数学问题。数学学习中的数量、数轴、统计图表等问题可以运用可视化或构建模型的策略来解决。当空间能力的干预促进儿童空间能力提升后，儿童可能会进一步认识到数学问题中的空间关系，并运用空间思维、策略去解决这些数学问题。[68]大多数研究从空间可视化、空间知觉和心理旋转三个维度进行空间能力干预，其效果也不尽相同。第一，空间可视化能力的发展提高了儿童空间想象或心理上操纵空间图形或物体的能力，为儿童依据所涉及的视觉和空间关系来解决数学问题提供了“心理黑板”。[69]例如，在解决缺失项问题时（2+？=5），空间可视化能力有助于儿童在头脑中再现具体形象化的物体，通过操纵物体的表象来解决具体的数学问题（盘子里一共有5个苹果，拿出来2个以后还剩几个）。第二，空间知觉能力的提升能够提高儿童从复杂背景判别图形或者把更复杂的图片分成几部分的能力。这不仅能帮助儿童在几何任务中辨别图形和空间关系，还能帮助儿童在非符号任务中辨别数字的具体形状、符号的意义，进行大小的比较以及算式的运算。第三，心理旋转能力涉及对视觉图像进行表征与旋转的心理空间加工，有助于儿童在解决数学问题的过程中自如地运用心理空间表征来解决问题，心理旋转能力的提高有助于儿童通过动态地操纵物体的表象来解决数数、口述应用题和加减运算等数学问题。[70]

（二）儿童年龄、干预方式、文化背景是影响干预效果的重要因素

本研究结果表明，空间能力干预对儿童数学能力发展的影响受被试年龄的调节效应显著。相比小学低年级儿童，对学前儿童进行空间能力干预能更好地提升其数学能力。一方面，学前阶段是儿童空间能力、数学能力发展的关键时期，[71]在这个时期进行空间能力干预，其效果可能会更加显著。另一方面，相比小学儿童，以具象思维为主的学前儿童的数学学习更依赖于空间体验和空间表征。空间体验指的是儿童对周围环境的感知、理解和互动，包括对形状、大小、位置、方向、距离等空间属性的认识。例如，儿童通过游戏和探索去理解上下、内外、前后、左右等空间概念，通过积木搭建、拼图等活动理解对称、平衡和图案等空间关系。空间表征也是儿童理解和解决数学问题的关键。例如，幼儿需要通过物体的移动（增加或拿走）来感知集合中数量的变化，通过积木的平铺、珠子的串联感知模式，或者积木的拼合感知图形间的关系。进入小学以后，儿童解决数学问题时的心理操作和策略会随着经验的积累而变化，有经验或者能熟练进行加减法运算的儿童的问题解决策略会逐渐多样化和自动化，如在解决运算问题时采用乘法口诀、组凑等简便、快捷的运算方式。[72]小学儿童解决数学问题时对外显的空间表征物的依赖降低了，其数学成绩与视觉空间工作记忆的相关程度下降了。[73]因此，空间能力干预对早期儿童数学能力的影响存在年龄差异。

本研究还发现，干预方式能够显著调节空间能力对早期儿童数学能力发展的影响。相比非具身操作，具身操作更能提高早期儿童的数学能力。这一研究结果在以往的研究中也得到了证实。[74]早期儿童处于前运算阶段或具体运算阶段，其思维缺乏抽象性，思维活动仍需要借助具体事物的支持。一方面，通过操作实物或身体动作有助于儿童表征抽象的空间关系和数量关系。例如，在进行心理旋转能力干预时，儿童通过对二维或三维物体进行旋转并从不同的角度进行观察能帮助其快速和准确地识别目标物体的镜像。这种旋转物体的身体动作可能有助于儿童形成一种植根于动作的空间关系的多模态认知表征，[75]使潜在的空间表征更容易内化与提取，并在随后解决数学问题时更容易激活共享的神经回路，运用相似的空间思维过程去解决数学问题。另一方面，具身操作能通过知觉符号提高儿童的数学能力。来自不同感觉通道的早期经验会存储于大脑不同区域，即不同系统中的神经元群，它们会形成单模态的知觉符号。[76]例如，儿童在进行积木游戏时，积木的大小、个数、形状和手指的触觉等信息会在不同的脑区形成知觉符号。干预中的每项任务都可能涉及多个知觉符号，彼此通过框架形成联系，从而组成模拟器。[77]当要求儿童对空间方位、数字大小进行判断时，与积木游戏中对应的触摸、运动和方位感觉经验就会被重新激活，儿童的躯体感知觉与抽象概念之间就建立起具身性联系。因此，具身操作更有利于儿童空间能力和数学能力的发展。

本研究证实了文化背景能够调节空间能力干预对早期儿童数学能力发展的影响。相比西方文化背景下的干预，东方文化背景下空间能力干预的效果更好。一方面，这种差异可能是由文化本身所导致的。社会文化理论指出，人类的认知发展起源并且紧密依赖于社会、历史和文化等因素，儿童早期的数学认知可能会因社会文化的不同而不同。[78]相比西方文化中的“短期取向”，东方文化的“长期取向”强调愉快应建立在刻苦学习并获得成果之后。[79]有实证研究发现，中国家长对早期儿童学习能力的焦虑程度较高，重视对子女学习兴趣、学习习惯的培养以及数学知识的学习。[80]另一方面，国内外研究实验设计的不同也在一定程度上导致了这种差异。纳入本元分析的国外研究大都是随机对照实验，对实验对象和情境都进行了较严格的控制，干预周期相对更短，受无关变量的影响较小。而纳入本元分析的国内研究大都采用准实验设计，研究周期相对更长，受无关变量的影响更大。这可能也是导致文化背景对儿童数学能力发展产生影响的重要原因。未来研究可以直接比较空间能力干预对不同文化背景下儿童数学能力的影响是否存在差异，在同一种干预方案中进一步探索文化背景对儿童数学经验和思维方式的影响。

（三）空间能力的维度、干预总时长不影响干预效果

本研究结果表明，不管是心理旋转干预，还是空间可视化干预或综合性干预，都能促进早期儿童数学能力的发展，但是三种干预的效应值无显著差异（p=0.157）。也就是说，空间能力的维度不调节干预效果。产生这一结果可能有两个方面的原因。一方面，空间能力的每一维度都是密切相关的，[81]在达到一定程度的训练后，空间能力的子维度之间会发生相互迁移，[82]针对某一维度的干预不仅能提高该维度的空间能力，还会提高其他维度的空间能力。另一方面，空间能力的每一维度都在一定程度上与数学能力相关。[83]

本研究还发现，干预时长也不能调节空间能力对数学能力的影响。首先，不同年龄阶段、不同个性特征的儿童存在认知水平、学习能力等方面的差异，对干预的反应与受益程度也存在一定的差异，难以探索出干预时长与干预效果的线性关系。其次，相比干预的总时长，干预的频率和单次时长可能更值得关注。在有的干预方案中，对儿童进行每天一次、连续7天的干预产生了中等的效应量（g=0.568）。[84]而另一位学者的干预方案中，是对儿童进行每周2次、连续7周的干预产生的是小效应量（g=0.131、0.126）。[85]最后，纳入元分析的大多数研究都只有即时后测，未能探索儿童数学能力的提升是否具有延时效应。未来研究可以设计不同干预时长和干预频率的方案，并对儿童进行延时后测，以进一步明晰干预时长对儿童数学能力发展的影响。

五、教育建议

（一）抓住早期儿童数学能力发展的关键期，创设有利于空间—数字联合表征的环境

本研究发现，空间能力的干预能提高早期儿童的数学能力，尤其是对学前期儿童来说，空间能力干预的迁移效果更好。这启示教育者应把握儿童数学能力发展的关键阶段，创设有利于儿童空间—数字联合表征的环境。首先，教育者需要认识到早期儿童数学学习与空间能力发展的内在关联，理解空间—数字联合表征环境对提高早期儿童大脑视空网络的结构水平的重要性。其次，设置不同的学习区域，如数学角、科学区、建筑区等，每个区域提供与数字和空间相关的活动和材料，如数字卡、计数棒、形状模板、几何图形玩具等，让儿童通过观察、比较和操作来理解数字和形状的关系。再次，创设飞行棋、积木建构等游戏环境。飞行棋能够为儿童提供融合空间与数字联合表征的心理数字线，帮助儿童更直观地感知数字之间的排列顺序和大小关系；积木建构游戏能够为儿童理解空间与数学之间的关系提供契机，如感知上下、左右等方位概念，理解整体与部分、组合与分解等数量与空间关系。最后，通过测量长度、重量、容量，规划空间，收纳游戏材料等实际活动让儿童去操作数字和空间。

（二）丰富早期儿童的具身空间体验，通过多样化的活动支持儿童的数学学习

本研究发现儿童在空间能力干预过程中使用具体的操作物或运用与物体移动相关的手势，其数学能力的提升效果会更好。这说明丰富的具身空间体验有利于儿童数学能力的发展。教育者应该意识到空间体验在儿童数学学习中的重要性，并提供适当的材料和环境来支持儿童的空间体验和数学探索。一方面，支持儿童的操作、感受和体验，帮助儿童在个体经验与数学本质之间找到联系点，形成自己的数学理解。例如，教师可在区域游戏中鼓励儿童通过自由堆叠、建构、触摸等方式，在图形移动、翻转或旋转变化的过程中感知不同图形的空间特征；在追逐玩耍的过程中对速度、方位、距离进行综合判断，体验不同的空间特性。另一方面，儿童数学概念的形成和发展是基于身体经验和无意识的认知机制。因此，在儿童建立大量感知和操作经验的基础上，教师可以鼓励其将直观的感性经验进行描述、表征和交流。例如，在操作活动的过程中鼓励儿童使用简单的记录表、统计表来表征操作结果，使用正确的数学语言与教师、同伴交流自己的操作结果，比较、分析自己与他人结果的异同。

（三）发挥空间思维在数学学习中的作用，鼓励早期儿童运用空间策略解决数学问题

空间思维在数学学习中扮演着至关重要的角色，它不仅能帮助儿童更好地理解数学概念，还能提高他们解决问题的能力。这启示教育者应关注数学知识本身的空间属性，支持鼓励儿童运用丰富的空间策略解决数学问题。首先，借助实物材料将抽象的数学知识转化为儿童可感、可察的直观活动，或者可参与的现实活动，促使他们在多感官的实物操作中解决数学问题。例如，在学习等分概念时，可以为儿童提供彩色纸片、剪刀等操作材料，通过图形的对折、裁剪等操作活动直观地理解等分概念。其次，运用图形视觉化策略，借助形象的图形将复杂的数学问题简单化、直观化。例如，在感知集合包含关系阶段，可以借助韦恩图形象地感知不同集合之间的关系，通过图形的交叠理解集合的共同元素。最后，发挥儿童的空间想象力，通过在脑海中动态地操作和变换表象，构建数学问题的直观模型。例如，通过旋转、平移和缩放等空间变换将复杂的图形进行分解和重组，让儿童更好地理解二维、三维物体的空间结构，掌握物体形状、大小和位置的关系。

参考文献：

[1]KOPONEN T， AUNOLA K， AHONEN T， et al. Cognitive predictors of single⁃digit and procedural calculation skills and their covariation with reading skill[J]. Journal of Experimental Child Psychology，2007，97（3）：220-241.

[2]全美数学教师理事会.美国学校数学教育的原则和标准[M].蔡金法，等译.北京：人民出版社，2004：24-25.

[3]文萍，张莉，李红，等.儿童执行功能对数学能力的预测模型[J].心理发展与教育，2007，23（3）：13-18.

[4]林崇德.学习与发展：中小学生心理能力发展与培养[M].北京：北京师范大学出版社，2003：12.

[5][83]谢芳.空间能力对数学能力的影响及其认知神经机制[D].重庆：西南大学，2020：4，24.

[6]MARTIN R B， CIRINO P T， SHARP C， et al. Number and counting skills in kindergarten as predictors of grade 1 mathematical skills[J]. Learning and Individual Differences，2014，34（8）：12-23.

[7]孙以泽.数学能力的成分及其结构[J].南京晓庄学院学报，2003，19（2）：97-99.

[8]LOHMAN D F. Spatial ability and g[C]//DENNIS I， TAPSFIELD P. Human abilities： their nature and measurement. New Jersey： Lawrence Erlbaum Associates，1996：97-116.

[9]UTTAL D H， MEADOW N G， TIPTON E， et al. The malleability of spatial skills： a meta⁃analysis of training studies[J]. Psychological Bulletin，2013，139（2）：352-402.

[10]LINN M C， PETERSEN A C. Emergence and characterization of sex differences in spatial ability： a meta⁃analysis[J]. Child Development，1985，56（6）：1479-1498.

[11]FRICK A. Spatial transformation abilities and their relation to later mathematics performance[J]. Psychological Research，2019，83（7）：1465-1484.

[12]DEHAENE S， BOSSINI S， GIRAUX P. The mental representation of parity and number magnitude[J]. Journal of Experimental Psychology： General，1993，122（3）：371-396.

[13]NEWCOMBE N S， LEVINE S C， MIX K S. Thinking about quantity： the intertwined development of spatial and numerical cognition[J]. Wiley Interdisciplinary Reviews： Cognitive Science，2015，6（6）：491-505.

[14]ZAGO L， PETIT L， TURBELIN M R， et al. How verbal and spatial manipulation networks contribute to calculation： an fMRI study[J]. Neuropsychologia，2008，46（9）：2403-2414.

[15]GERSMEHL P J， GERSMEHL C A. Spatial thinking by young children： neurologic evidence for early development and “educability”[J]. Journal of Geography，2007，106（5）：181-191.

[16][33]康丹，文鑫.心理旋转训练对5～6岁儿童空间能力和数学能力的影响[J].心理发展与教育，2020，36（1）：19-27.

[17]ADAMS J， RESNICK I， LOWRIE T. Supporting senior high⁃school students’ measurement and geometry performance： does spatial training transfer to mathematics achievement？[J]. Mathematics Education Research Journal，2023，35（4）：879-900.

[18][24][51]HAWES Z， MOSS J， CASWELL B， et al. Effects of mental rotation training on children’s spatial and mathematics performance： a randomized controlled study[J]. Trends in Neuroscience and Education，2015，4（3）：60-68.

[19]GILLIGAN K A， HODGKISS A， THOMAS M S C， et al. The developmental relations between spatial cognition and mathematics in primary school children[J]. Developmental Science，2019，22（4）：1-69.

[20]MIX K S， LEVINE S C， CHENG Y L， et al. Separate but correlated： the latent structure of space and mathematics across development[J]. Journal of Experimental Psychology： General，2016，145（9）：1206-1227.

[21][36]康丹，胡姿，蔡术，等.主题积木游戏对5～6岁儿童数学能力和空间技能发展的干预效果[J].中国心理卫生杂志，2020，34（4）：332-336.

[22]HUNG P H， HWANG G J， LEE Y H， et al. A cognitive component analysis approach for developing game⁃based spatial learning tools[J]. Computers & Education，2012，59（2）：762-773.

[23][47][68]CHENG Y L， MIX K S. Spatial training improves children’s mathematics ability[J]. Journal of Cognition and Development，2014，15（1）：2-11.

[25][35]王楚凡.4～5岁儿童数概念发展与空间能力的关系研究[D].上海：华东师范大学，2020： 110，93-115.

[26][43]RODÁN A， GIMENO P， ELOS [U]A M R， et al. Boys and girls gain in spatial， but not in mathematical ability after mental rotation training in primary education[J]. Learning and Individual Differences，2019，70（2）：1-11.

[27]霍夫斯泰德.文化与组织：心理软件的力量：第二版[M].李原，孙健敏，译.北京：中国人民大学出版社，2010：51.

[28]刘君红，许文丽.中美家庭教育跨文化比较研究[J].教育评论，2020，36（4）：158-163.

[29][63]HAWES Z C K， GILLIGAN⁃LEE K A， MIX K S. Effects of spatial training on mathematics performance： a meta⁃analysis[J]. Developmental Psychology，2022，58（1）：112-137.

[30]NEWCOMBE N S， FRICK A. Early education for spatial intelligence： why， what， and how[J]. Mind， Brain and Education，2010，4（3）：102-111.

[31]HECKMAN J J， MASTEROV D V. The productivity argument for investing in young children[J].Applied Economic Perspectives and Policy，2007，29（3）：446-493.

[32]康丹，文敏，张颖杰.儿童精细动作技能与数学能力的关系：一项元分析[J].心理科学进展，2023，31（8）：1443-1459.

[34]赵振国.3～6岁儿童数量估算、数数能力及视觉空间认知能力发展关系的研究[D].上海：华东师范大学，2009：151-170.

[37]高木子.结构游戏对中班幼儿几何图形感知影响的实验研究[D].石家庄：河北师范大学，2018：11-26.

[38]程欢.积木游戏对5～6岁幼儿几何形体认知的影响实验研究[D].天津：天津师范大学，2017：16-25.

[39]蔡黎曼.积木游戏对学前儿童认知能力发展的影响[J].华南师范大学学报（社会科学版），2018 （05）：89-95.

[40]魏厚珠.积木游戏对三年级学生空间能力与数学能力的影响[D].福州：福建师范大学，2022：15-31.

[41]蒋慧.6～8岁儿童空间能力与数学成就的关系[D].重庆：西南大学，2019：29-35.

[42]杨琼，王妮妮.积木建构游戏对4～5岁儿童早期数学能力的影响[J].幼儿教育，2022，41（12）：17-21+27.

[44][84]CHEUNG C N， SUNG J Y， LOURENCO S F. Does training mental rotation transfer to gains in mathematical competence？ Assessment of an at⁃home visuospatial intervention[J]. Psychological Research，2020，84（7）：2000-2017.

[45]MIX K S， LEVINE S C， CHENG Y L， et al. Effects of spatial training on mathematics in first and sixth grade children[J]. Journal of Educational Psychology，2021，113（2）：304-314.

[46]GILLIGAN K A， THOMAS M S， FARRAN E K. First demonstration of effective spatial training for near transfer to spatial performance and far transfer to a range of mathematics skills at 8 years[J].Developmental Science，2020，23（4）：1-18.

[48]CORNU V， SCHILTZ C， PAZOUKI T， et al. Training early visuo⁃spatial abilities： a controlled classroom⁃based intervention study[J]. Applied Developmental Science，2019，23（1）：1-21.

[49]XU C， LEFEVRE J A. Training young children on sequential relations among numbers and spatial decomposition： differential transfer to number line and mental transformation tasks[J]. Developmental Psychology，2016，52（6）：854-866.

[50][85]SCHMITT S A， KORUCU I， NAPOLI A R， et al. Using block play to enhance preschool children’s mathematics and executive functioning： a randomized controlled trial[J]. Early Childhood Research Quarterly，2018，44（3）：181-191.

[52][64]HAWES Z， MOSS J， CASWELL B， et al. Enhancing children’s spatial and numerical skills through a dynamic spatial approach to early geometry instruction： effects of a 32⁃week intervention[J]. Cognition and Instruction，2017，35（3）：236-264.

[53]MCDOUGAL E， SILVERSTEIN P， TRELEAVEN O， et al. Assessing the impact of LEGOR construction training on spatial and mathematical skills[J]. Developmental Science，2024，27（2）：1-19.

[54]ZHANG D W， ZAPHF A， KLINGBERG T. Resting state EEG related to mathematical improvement after spatial training in children[J]. Frontiers in Human Neuroscience，2021，15（7）：1-10.

[55]LOWRIE T， LOGAN T. Spatial visualization supports students’math： mechanisms for spatial transfer[J]. Journal of Intelligence，2023，11（6）：127-147.

[56][74]GILLIGAN⁃LEE K A， HAWES Z C， WILLIAMS A Y， et al. Hands⁃On： investigating the role of physical manipulatives in spatial training[J]. Child Development，2023，94（5）：1205-1221.

[57]任志洪，赖丽足.心理学元分析方法： 理论、案例与操作[M].北京：中国人民大学出版社，2023：181.

[58]BORENSTEIN M， HEDGES L V， HIGGINS J P T， et al. A basic introduction to fixed⁃effect and random⁃effects models for meta⁃analysis[J]. Research Synthesis Methods，2010，1（2）：97-111.

[59]THORNTON A， LEE P. Publication bias in meta⁃analysis： its causes and consequences[J]. Journal of Clinical Epidemiology，2000，53（2）：207-216.

[60]HUEDO⁃MEDINA T B， SÁNCHEZ⁃MECA J， MARN⁃MARTNEZ F， et al. Assessing heterogeneity in meta⁃analysis： Q statistic or I2 index？[J]. Psychological Methods，2006，11（2）：193-206.

[61]HEDGES L V， VEVEA J L. Fixed⁃and random⁃effects models in meta⁃analysis[J]. Psychological Methods，1998，3（4）：486-504.

[62]ROTHSTEIN H R， SUTTON A J， BORENSTEIN M. Publication bias and meta⁃analysis： prevention， assessments and adjustments[M]. Chichester： John Wiley，2005：261-286.

[65]PATRO K， FISCHER U， NUERK H C， et al. How to rapidly construct a spatial⁃numerical representation in preliterate children （at least temporarily）[J]. Developmental Science，2016，19（1）：126-144.

[66]DEHAENE S， SPELKE， PINEL P， et al. Sources of mathematical thinking： behavioral and brain⁃imaging evidence[J]. Science，1999，284（5416）：970-974.

[67]胡林成.空间认知与数学能力的关系：认知模型、神经机制及教育[J].内蒙古师范大学学报（教育科学版），2023，36（6）：14-20.

[69]BATES K E， GILLIGAN L K， FARRAN E K. Reimagining mathematics： the role of mental imagery in explaining mathematical calculation skills in childhood[J]. Mind， Brain and Education，2021，15（2）：189-198.

[70]LOURENCO S F， CHEUNG C N， AULET L S. Is visuospatial reasoning related to early mathematical development？ A critical review[C]//AVISHAI H， WIM F. Heterogeneity of function in numerical cognition. London： Academic Press，2018：177-210.

[71]白佳.试论吸收性心智及儿童敏感时期特征[J].科技资讯，2019，17（36）：246-247.

[72]李姗姗，黄诗韵，郭力平.基于24点四则运算游戏的儿童数学问题解决策略观察与评估[J].现代中小学教育，2024，40（2）：32-37.

[73]RAGHUBAR K P， BARNES M A， HECHT S A. Working memory and mathematics： a review of developmental， individual difference， and cognitive approaches[J]. Learning and Individual Differences，2010，20（2）：110-122.

[75]BARSALOU， LAWRENCE W. Grounded Cognition[J]. Annual Review of Psychology，2008，59（1）：617-645.

[76]FOGLIA L， WILSON R A. Embodied cognition[J]. Wiley Interdisciplinary Reviews： Cognitive Science，2013，4（3）：319-325.

[77]卢凤，黄晶，赵源.从具身认知看手指在早期数学教学中的作用与启示[J].数学教育学报，2023，32（1）：55-58.

[78]SAXE G B. The mathematics of child street vendors[J]. Child Development，1988，59（5）：1415-1425.

[79]周士民，王君.文化差异下东西方数学教育比较——梁贯成教育思想简介[J].数学通报，2014， 53（11）：5-7.

[80]肖鲜.幼升小阶段幼儿家长的教育焦虑研究[D].成都：四川师范大学，2020：24-28.

[81]NEWCOMBE N S， SHIPLEY T F. Thinking about spatial thinking： new typology， new assessments[C]//JOHN S G. Studying visual and spatial reasoning for design creativity. Dordrecht： Springer Netherlands，2014：179-192.

[82]UTTAL D H， MEADOW N G， TIPTON E， et al. The malleability of spatial skills： a meta⁃analysis of training studies[J]. Psychological Bulletin，2013，139（2）：352-402.

Can Early Children’s Spatial Ability Intervention Improve Their Mathematical Abilities？

—Meta⁃Analysis Based on Experimental or Quasi⁃experimental Research

KANG Dan， ZHANG Yingjie， ZHANG Xiangyi

（School of Education Science， Hunan Normal University，Changsha 410081 China）

Abstract： Spatial ability is closely related to mathematical ability， but whether spatial ability intervention can improve early children’s mathematical ability remains unclear. In order to further clarify the impact of spatial ability intervention on early children’s mathematical ability， this study used meta⁃analysis to integrate and analyze 24 domestic and foreign related studies. The results show that previous studies have proved that spatial ability intervention can improve early children’s mathematical ability. Children’s age， intervention methods and cultural background are important factors affecting the intervention effect， while the dimension of spatial ability and the total duration of intervention have no significant impact on intervention effectiveness. It is suggested that educators should seize the critical period of early children’s mathematical ability development and create an environment conducive to children’s spatial⁃digital joint representation， enrich early children’s embodied space experience and support children’s math learning through diverse activities， play the role of spatial thinking in mathematics learning and encourage early children to use spatial strategies to solve math problems.

Key words： spatial ability； mathematical ability； meta⁃analysis

（责任编辑：黎勇）

*基金项目：2023 年度湖南省普通高等学校教学改革研究“学前儿童游戏课程教师技能的‘高校—基地—幼儿园’协同培育模式构建的行动研究”（编号：HNJG-20230260）

**通信作者：康丹，湖南师范大学副教授，博士