旋转多“一点” 理解更透彻

［摘 要］旋转运动的本质是图形上的每一个点都绕着旋转中心，按旋转方向旋转了相同的角度。教师需要站在学生学习的视角，提供结构化的学习材料，通过连续的递进性学习任务，促进学生体验、感受和认识旋转的本质。

［关键词］旋转；学习视角；结构化材料

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2024）35-0061-04

【课前思考】

旋转作为一种保持特定点或轴不变的连续变换，相较于平移和轴对称，其概念更为复杂。在教学过程中发现，学生虽然已经在低学段接触过旋转，但在进一步学习旋转运动时，仍将旋转简单等同于转动，未能深刻理解旋转运动的核心特征：图形上的每一点均绕旋转中心按相同方向旋转相同角度。针对这一教学现状，笔者尝试通过提供结构化学习材料和设计递进式学习任务，促进学生深入体验和认识旋转的本质，以提升学生对旋转概念的理解，实现了“旋转多‘一点’，理解更透彻”的教学目标。

【课中实践】

一、引入新课

师（板书课题“旋转”，出示生活中常见的旋转，如图1）：二年级的时候我们已经初步认识了旋转，今天我们进一步来学习图形的旋转。

【设计意图：借助学生熟悉的生活中的旋转现象唤起学生的前经验，简单明了地引入新课。】

二、学习新知

（一）线的旋转

1.认识旋转的要素

（1）旋转角度

师（出示线段AB）：这是一条线段。想象一下，若将线段[AB]旋转，旋转后的图形会是怎样的呢？

师：大家尝试旋转了线段[AB]，为何结果各异？

生1：因为有的旋转角度较大，有的较小。

师：确实如此，旋转角度的差异导致了结果的不同。

（2）旋转方向和旋转中心

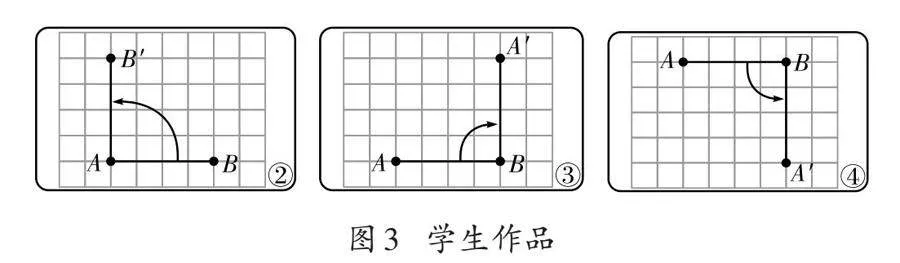
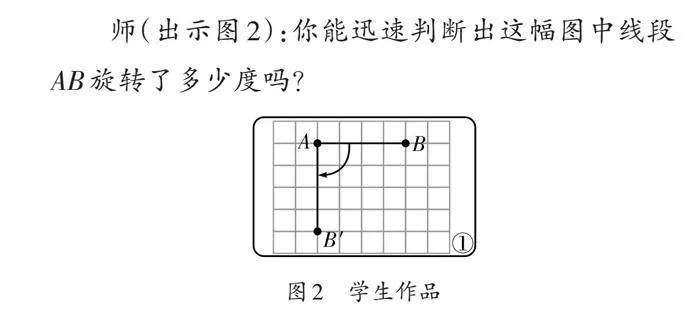
师（出示图2）：你能迅速判断出这幅图中线段[AB]旋转了多少度吗？

生2：线段[AB]旋转了90°，因为它与旋转后的线段形成了一个直角。

师：我们可以通过想象线段旋转的过程，观察旋转前后形成的夹角来判断旋转角度（演示旋转的动态过程）。

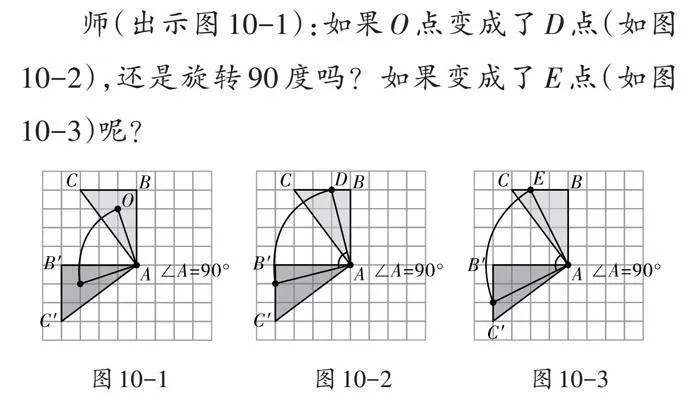
师（出示图3）：快速判断图中线段[AB]的旋转角度。（学生快速判断都旋转了90°）

师：这几幅图都旋转了90°，为何结果仍然不同？

生3：因为方向不同，有的向下旋转，有的向上旋转。

生4：有的顺时针旋转，有的逆时针旋转。

师：描述旋转时，我们常用顺时针和逆时针来表示方向（出示钟表，动态演示指针旋转）。现在，伸出手指和老师一起指一指，与钟表时针旋转方向一致的是顺时针，相反的是逆时针。

师：快速判断图2、图3中线段[AB]的旋转方向。

师：图2中的①和图3中的③都是顺时针旋转，为何结果不同？

生5：因为①以[A]点为中心旋转，③以[B]点为中心旋转。

师：图形旋转时围绕的点称为旋转中心。①②的旋转中心是[A]点，③④的旋转中心是[B]点，旋转中心同样重要。

【设计意图：在前测中发现，学生对于旋转角度的感知最为敏感，其次是旋转方向，而旋转中心则常被忽略。教材编排的钟表素材有助于学生理解旋转角度，但由于其旋转中心固定且方向唯一，不利于学生全面理解旋转方向和旋转中心对旋转效果的影响。因此，采用线段旋转作为教学素材来帮助学生认识旋转的三要素时，由于线段旋转不受旋转中心、方向和角度的限制，学生可以自由探索旋转的多种可能性。按照学生对旋转要素感知的强弱顺序——“角度→方向→中心”，结构化地展示了学生前测中的典型作品，并辅以动态旋转演示，加深学生对旋转要素的理解。】

（3）旋转描述

师：知道了旋转中心、方向和角度，能否准确描述图形的旋转呢？（出示图4）“线段[AB]绕[A]点顺时针旋转90°”描述的是哪幅图？

生6：图4中的①。

师：还有其他可能的情况吗？（学生观察后确认没有）。当旋转中心、方向和角度都确定时，旋转结果也是唯一的。

师：你能像这样描述其他几幅图的旋转情况吗？和你的同桌交流一下。

【设计意图：在学生掌握了旋转的三要素之后，让学生根据描述选择对应图形，不仅为学生提供了描述旋转的表达范式，还让他们认识到当旋转中心、方向和角度确定时，旋转结果的唯一性。】

2.体验旋转的本质

师（出示图5）：线段[AB]处于竖直位置，若将其绕[A]点逆时针旋转90°，请问旋转后的线段[AB]将位于何处？请观察线段上的[C]点，思考在线段旋转过程中，[C]点的运动轨迹及其旋转角度。

生1：线段[AB]逆时针旋转90度后，会落在水平横线上，长度为4格；[C]点也是绕[A]点旋转的，旋转后得到了一个直角，因此[C]点旋转了90°。

师：为什么[C]点的旋转轨迹是弯曲的，而不是直线运动？你是怎么理解的？

生1（指向[C]点的旋转轨迹，如图6-1）：[C]点是绕[A]点旋转的，不是直接移动，所以轨迹是弯曲的。

师：非常好，这说明[C]点在旋转过程中，与[A]点的距离保持不变。让我们一起来观察（动态演示[C]点随线段[AB]旋转）。可以将[C]点视为线段[AC]的端点（演示[C]点随线段[AC]旋转），旋转后，[AC]与[AC′]之间的夹角为直角，说明[C]点绕[A]点旋转了90°。

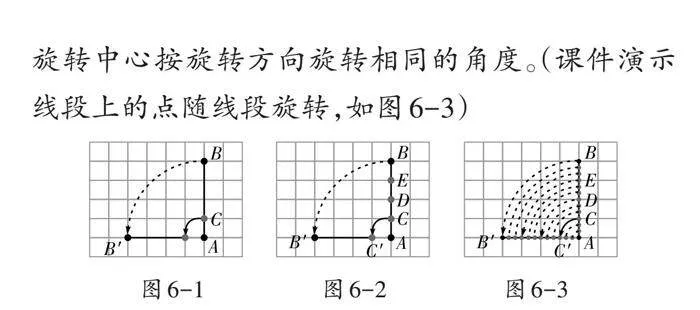
师：假设线段上还有[D]点和[E]点（如图6-2），想象一下，它们可以看作是哪条线段的端点？它们分别旋转了多少度？

生2：[D]点可以看作是线段[AD]的端点，旋转了90°；[E]点可以看作是线段[AE]的端点，同样旋转了90°（动态演示[D]点、[E]点分别随线段[AD]、[AE]旋转）。

师：通过刚才的探讨，有什么发现？

生3：线段旋转时，线段上的点都会随线段一起旋转相同的角度。

师：线段旋转过程中，线段上的每个点都会绕旋转中心按旋转方向旋转相同的角度。（课件演示线段上的点随线段旋转，如图6-3）

【设计意图：先选取线段上的代表性点[C]，探讨其旋转情况，帮助学生深入理解旋转的概念；接着类比分析[D]点、[E]点的旋转，推广到线段上所有点的旋转，从而将线段旋转简化为点的旋转，使学生理解“线段旋转过程中，线段上的每个点都绕旋转中心，按旋转方向旋转相同的角度”。】

（二）形的旋转

1.初步感受形的旋转

师：刚才我们研究的线段[AB]其实是三角形[ABC]的一条边（补上线段[BC]、[AC]，形成三角形[ABC]）。想象一下，如果三角形[ABC]旋转，结果会怎样呢？（动态演示三角形旋转）请仔细观察三角形[ABC]是如何旋转的。

生1：三角形[ABC]绕[A]点逆时针旋转90°。

师（出示图7）：绕[A]点旋转很容易看出是逆时针，但你是如何判断三角形旋转了90°的呢？接下来，请大家带着这个问题完成下面的任务。（1）找一找：你能从不同的地方找到三角形[ABC]旋转了90°的痕迹吗？请找一找并用三角板验证。（2）想一想：三角形上的[O]点在旋转过程中会如何移动？它旋转了多少度？请在图上标出你的推断。可以使用信封中的小三角形辅助你的研究。

生2（出示图8）：我发现[AB]与[AB′]的夹角是90°，[AC]与[AC′]的夹角也是90°，这说明三角形[ABC]旋转了90°。

师：像这样，[AB]和[AB′]就是一组对应边，[AC]和[AC′]也是一组对应边。你是通过对应边的旋转角度来判断三角形[ABC]旋转的度数的，非常清晰。

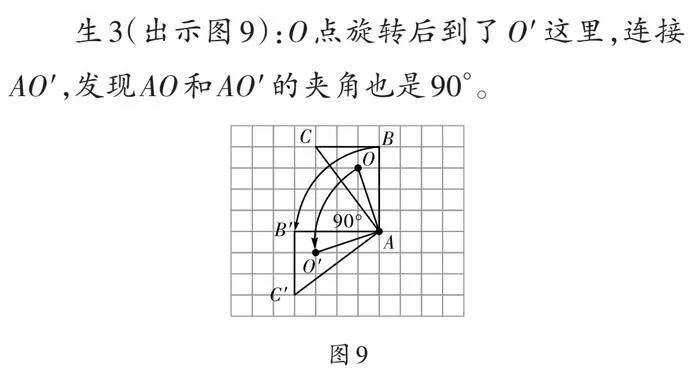
生3（出示图9）：[O]点旋转后到了[O′]这里，连接[AO′]，发现[AO]和[AO′]的夹角也是90°。

师：有这么多点，为什么要连接[A]点和[O]点？

生4：因为三角形是绕点[A]旋转的，所以[O]点也会绕[A]点旋转。

师：图形旋转时，图形上的点也会围绕旋转中心旋转。现在让我们一起来观察[O]点的旋转过程（使用几何画板演示）。

2.加深理解形的旋转

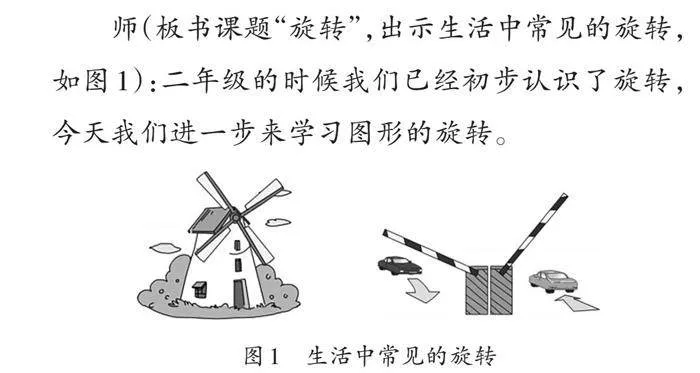
师（出示图10-1）：如果[O]点变成了[D]点（如图10-2），还是旋转90度吗？如果变成了[E]点（如图10-3）呢？

师：通过这些研究，你们有什么发现？

生5：在三角形[ABC]旋转过程中，三角形上的所有点都绕旋转中心旋转了90度。这个面上的每条边、每个点都旋转了相同的角度。

【设计意图：在学生理解了线段旋转的本质后，将概念由“线”拓展到“形”，选取三角形上的代表性O点进行探讨，帮助学生理解形状旋转的本质。通过类比探讨D点、E点的旋转，能帮助学生将面的旋转归结为线段和点的旋转，从而直观理解面旋转时每条边和每个点都旋转相同角度的概念。】

3.初步定位形的旋转

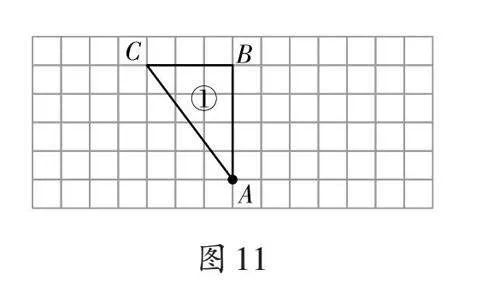
师（出示图11）：我们将三角形[ABC]标记为三角形①。三角形①以[A]点为中心顺时针旋转90度，形成三角形②。三角形②会出现在什么位置？

师：当一个面旋转时，面上的所有线段都会旋转相同的角度。因此，只需确定关键线段的位置，即可推断出旋转后的形状。（课件先展示边[AB]的旋转，再展示整个三角形的旋转）

师：假设三角形①绕[A]点顺时针旋转180度得到三角形③，逆时针旋转90度得到三角形④。三角形③和④各自会位于何处？

师：我们刚刚通过不同的旋转方式得到了四个三角形。观察①②③④的顺序，这个图形是如何形成的？

生7：是三角形①绕[A]点依次顺时针旋转90度得到的。

师（出示图12）：让我们一起来观察这个过程。（演示旋转）如果每次旋转的角度更小，会出现什么情况？（学生想象后，动画演示）

【设计意图：在学生理解了点、线、面旋转的本质后，找图形的活动能让学生根据旋转的描述想象和寻找旋转后图形的位置，学生体会到可以将形的旋转分解为关键线或点的旋转，知道可以通过找关键线段或关键点来确定形的位置。】

三、练习提高（略）

四、回顾总结（略）

【课后反思】

一、基于学生学习的视角

教学中，教师除了要关注学生的“已知”“能知”及学习过程中的“难知”，还要特别关注学生学习中的“怎知”，即站在学生学习的视角，尝试以学习者的角色，分析学生是怎么认识和学习新知的。学生对于旋转三要素——角度、方向、中心的感知顺序往往是从直观的角度开始，然后是方向，最后才是中心。因此，先将“旋转中心固定，旋转方向唯一”的钟表素材替换成线段素材，再按学生对旋转要素感知的强弱顺序“角度→方向→中心”，结构化地呈现典型作品，就能促进学生对旋转要素的理解。这种基于学生视角的教学设计，不仅能够提升教学效果，还能让学生在学习过程中产生共鸣，增强学习的积极性和主动性。

二、提供结构化的学习素材

为了帮助学生将旋转的认知从感性认识上升到本质理解，教师有意设置了两个层次递进的学习任务——首先是线段[AB]的旋转，然后是三角形[ABC]的旋转，并在此基础上探究单个点的旋转情况。在这两个任务中，教师“无中生有”地设置了探究一个点的旋转情况的研究任务。线的旋转和形的旋转，因为多了探究“无中生有”的这“一点”旋转情况，就使教学走向了深刻。因为这“一点”有力促进了学生对旋转本质的透彻理解，从而达到了“旋转多‘一点’，理解更透彻”的教学效果。

三、给予通顺的内在逻辑

在学生理解了旋转的三要素之后，教师可以通过设计“据话选图”的环节，让学生在实践中体会当旋转的三要素确定时，旋转的结果是唯一的。此外，为了让学生更好理解旋转运动过程中图形上的每一个点都绕着旋转中心，按旋转方向旋转了相同的角度这一本质，整个教学过程应该围绕将线的旋转归结为点的旋转，以及将形的旋转归结为点或线的旋转这一核心逻辑展开：在探究线段[AB]的旋转时，引导学生关注线段上某点的旋转情况；在探究三角形[ABC]的旋转时，引导学生关注三角形上某点或某线的旋转情况。这样的教学设计将面的旋转归结到线或点的旋转上，将线的旋转归结到点的旋转上，有助于学生构建一个从面到线再到点的清晰且通顺的内在逻辑结构，从而更加系统地理解和掌握旋转的概念。

（责编 金 铃）