建构主义视角下数学课堂“质疑思维”的探索与实践

［摘 要］在建构主义视角下，学生的学习会经历同化和顺应阶段。在此过程中，数学课堂的“质疑思维”显得尤为重要。文章通过揭示当前课堂中普遍存在的师生不质疑现状，并剖析其成因，从三个方面对课堂“质疑思维”进行探索和实践，帮助学生在共学模式下获得质疑话语权，在回访课堂中使学生收获质疑的反馈，在争辩反思中让学生体会质疑的魅力。

［关键词］建构主义；质疑思维；小学数学

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2024）35-0090-03

建构主义理论认为，知识的获取需以学生的主动建构为基础。当遇到新的学习对象时，学生会在原有的基础上进行建构，从而实现知识的扩充，此为“同化”；当遇到新的挑战和刺激时，原来的认知基础无法维持平衡，学生就会建立新的认知体系，此为“顺应”。由此可见，学生主动探索知识，在原有的认知基础上不断发展，这才是真正的学习过程。而在建构的过程中，有一项要素在数学课堂中显得尤为重要，即质疑。有质疑，说明学生在接触新的数学问题时，受到了新的激发，打破了原有的认知平衡，这标志着知识建构的开始；有质疑，说明学生深入思考，表明他们是主动探究问题，而非被动接受知识。那么，关于如何在数学课堂上建立“质疑思维”，笔者将基于教学实践的具体场景展开论述。

一、直击现场——呈现师生不质疑的现状

（一）教师不质疑

一节练习课上，教师带领学生探索一个数学问题。

有甲、乙两个容器，将两个容器都装满水，已知甲的容量是乙的9倍，如果从甲容器中倒1升的水到乙容器，甲、乙两个容器中的水就一样多。请问：甲容器中原来有多少升水？

教师提出问题后，随即组织学生思考、交流自己的想法。很快，学生就得到了两种解法。之后教师引导学生思考：这两种解法有什么共同之处？学生通过交流，很快也找到了两种解法的共同之处。

此时，教师为课堂上热闹的探讨氛围感到欣慰：“同学们，你们真的太会思考了！”然而，一个“尖锐”的声音打破了原本热闹的课堂氛围：“老师，不对啊！甲容器和乙容器都装满了水，乙容器怎么还能装得下甲容器倒出的水呢？”

若问题的条件是不成立的，又如何引导学生探究呢？面对学生的质疑，教师顿时感到困惑，不知该如何回应。在准备数学问题时，教师是否质疑过所准备的问题在实际生活中是否真实可行？如果教师所准备的数学问题缺乏严谨性和科学性，又怎能将数学质疑的精神传承给学生呢？笔者认为，这是值得教育工作者深思的问题。在日常教学中，教师要时刻反思自己是否遵循数学的严谨性、科学性？是否用质疑的眼光去看待数学问题？要想帮助学生学会质疑，教师首先要善于质疑。

（二）学生不敢疑

一节数学公开课上，教师出示一个实际问题。

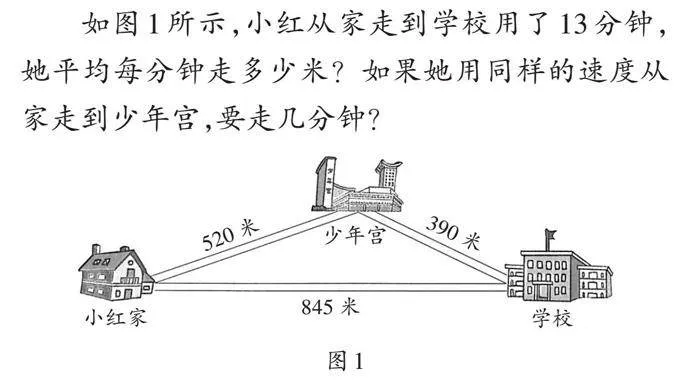
如图1所示，小红从家走到学校用了13分钟，她平均每分钟走多少米？如果她用同样的速度从家走到少年宫，要走几分钟？

一名学生举手回答，并完整地描述了自己的想法：先求出速度，845÷13=65（米/分），再用小红家到少年宫的距离除以速度得到时间，520÷65=8（分钟）。笔者坐在教室后方，观察到一名学生在他的导学单上是这样写的：845÷13=65（米/分），845-520=325（米），325÷65=5（分钟），13-5=8（分钟）。当教师提问是否还有不同的解法时，该名学生神情局促，迟迟不敢举手。从该名学生的表情上可以看出来，当他听到举手回答的同学只用2个算式求解时，他否定了自己的多步解法。课下，笔者耐心询问该名学生：“课上，为什么没有展示自己的解法呀？”他害羞地回答：“当时我发现自己的算式较多，我的方法跟别人不一样，肯定不对。”

听完该名学生的解释，笔者陷入深思：学生为什么会因为自己的解法不够简洁而觉得它是错误的呢？学生若能明晰并梳理自己的解法，便不会如此缺乏自信。究其原因，该名学生在主动构建方法时，思路逻辑混乱，进而导致自己不敢质疑，而是直接自我否定。试想，这样的情况在日常课堂中肯定不乏少数。可见，学生在课堂上的质疑意识、质疑能力和质疑水平仍有待提升。

（三）教师不重疑

一节数学公开课上，教师教学“两、三位数除以两位数的笔算（四舍试商法）”内容时，带领学生探索192÷39的笔算除法。此时，教师提出：“把39看作40来试商（“五入”试商），得出商是4，余数是36。”就在这个时候，一名学生提出疑问：“老师，如果变成199÷39，把39看作40来试商（“五入”试商），就得到商是4，但是这个商是不对的！”教师的教学被这名学生的发言打断，教师不知如何是好，仅回应道：“这个情况不是今天学习的，我们后面再学习。”这样的回答就草草回应了一个精彩的“质疑”。

公开课结束后，笔者细思：该名学生为什么会提出这样的质疑呢？从建构主义理论的角度去思考，其实该名学生正在主动建构知识，在顺应的过程中，他发现了新的激发点，这恰恰表明其正处于真实的知识建构之中。笔者认为，面对学生处于认知过程时，教师应当适时引导，助力学生完善其知识体系。

二、拈断髭须——深思不质疑现状的成因

通过对上述课堂实例的分析，可以发现部分数学课堂中，质疑的氛围仍较薄弱。基于真实案例，笔者将从以下三个方面对当前课堂中普遍存在的不质疑现状的成因进行阐述。

（一）思想固着，未树立正确的教学观念

从上述课堂实例中可以发现：部分数学课堂中质疑氛围的缺乏与教师的教学行为存在着深刻的关联，这一现象主要折射出了部分教师的教学观念较为落后。首先，在教学过程中，若教师没有秉持严谨的科学态度，又怎么能引导学生形成严谨的求学态度呢？其次，部分教师自我定位为单纯的知识传授者，而不是教学的组织者、引导者和合作者。从建构主义的角度出发，学生的认知发展须经历一个逐步完善的过程，需在原有认知基础上实现转变。如果教师的角色定位错误，教师就很难帮助学生经历知识的建构过程，就会导致学生容易陷入被动接受知识的困境。最后，部分教师对数学课堂教学中学生的质疑行为重视不足，甚至认为学生的质疑会影响教学进度，很多时候不希望这样的“插曲”出现。殊不知，教学中出现的这些“插曲”，正是学生深度学习的体现。因此，教师重视数学课堂上学生的质疑行为，显得尤为重要。

（二）视而不见，不重视学生完整的认知过程

在上述提及的第二个课堂实例中，学生在课堂上主动探索了相关量的关系，形成了自己的想法，但是学生对自己的想法不能清晰地解释出来，这说明其认知过程还不够完整。此类情形在学生中是普遍存在的，如果教师没有重视这样的过程，那么学生的质疑精神或将逐渐消退，这无疑对学生的学习成效产生不利影响。在实际教学中，教师要充分关注学生认知过程的完整性，促使学生学习信心日益增强，质疑勇气与能力逐步提升，进而使数学课堂逐步形成质疑的良好氛围。

（三）一叶障目，忽略学生认知中的原生问题

学生在学习新知的过程中，会经历同化和顺应这一过程。在这样的学习过程中，学生需要自主进行知识建构。在建构过程中，学生有很多思考的共性问题，这样的问题往往会被部分教师忽略。若学生不能主动地解决这些共性问题，其知识建构的进程将难以顺利进行。比如，在上述提及的第三个课堂实例中，有学生在主动建构知识的时候，质疑了“五入”试商所得结果的准确性。在教学中，教师如果总是忽略学生的这类问题，长此以往，将导致学生对知识的掌握不够牢固，其知识结构亦将呈现不完善的状态。

三、力学笃行——深化数学课堂“质疑思维”的实践策略

（一）共学，在共学模式下拥有质疑话语权

基于上述成因分析，笔者认为教师可以尝试一些教学模式，构建数学课堂中良好的“质疑思维”。例如，在知识探究环节，可推行小组内协同学习的方式，由小组长负责组织组内活动，并确保其余成员分工清晰明确；教师规划小组共学的内容，并引导学生在既定框架下进行共学；小组共学结束后，教师鼓励学生在总结阶段提出各自的质疑。

例如，在教学“确定位置”时，笔者安排以下组内共学任务。

①想一想，（2，4）和（4，2）表示的位置一样吗？

②小王和小军在同一列，小军的位置用数对表示是（2，4），小王的位置用数对表示可能是什么？

③小陈和小军在同一行，小军的位置用数对表示是（2，4），小陈的位置用数对表示可能是什么？

④对于用数对来确定位置，你有什么疑问吗？

对于第4个任务，学生提出了学习中遇到的困惑，如为什么要先写列再写行？是不是所有的位置都可以用数对表示？为什么不能从右往左数，得到第几列呢？

又如，在教学“商不变的规律”时，笔者安排以下组内共学任务。

给出除法算式：100÷20=5。

①如果要使这道算式的商还是5，除数和被除数可以怎样变化呢？

②先提出你的猜想，再举例子，验证你的猜想。

③你得出了怎样的结论呢？

在组内共学的模式下，学生主动思考新的问题，主动调动已有的经验解决新的问题，这充分体现了建构主义的教学理念。同时，在组内共学的模式下，学生产生的质疑是真实且生动的，他们敢于在小组内部表达自己的疑惑，乐于分享并探讨各自的疑问。整个学习过程中，学生均展现出积极的学习态度。

（二）回访，在回访课堂中收获质疑的反馈

所谓回访模式，主要指两种方式。第一种，当学生在课堂上没有机会表达自己的想法时，可以让学生将自己的想法写下来，课下跟教师进行交流，以此弥补课堂质疑机会的不足。第二种，当课堂讨论中出现具有争议性的观点，且多数学生因时间限制未能充分思考该观点的正确性时，可为学生提供额外的时间，在课后继续深入探究这一争议性想法，且于次日专门设置回访课堂，组织全班学生共同讨论并解决该问题。如此，学生的思考时间得以充分保障，其知识建构的过程亦能得以完整呈现。

回顾上述第一个课堂实例，在实际教学中，如果教师在课堂巡视中发现学生有不同的解法时，教师应鼓励学生一起来探索这一解法的正确性。可见，适当开展的回访课堂，是帮助学生完善知识的建构过程的有效“脚手架”。

（三）争辩，在关键问题中体会质疑的魅力

在顺应的学习过程中，学生会产生很多原生的问题，这些问题是牢固掌握新内容的关键。教师在原生问题中引发学生质疑、争辩，是培养其质疑能力的有效途径。

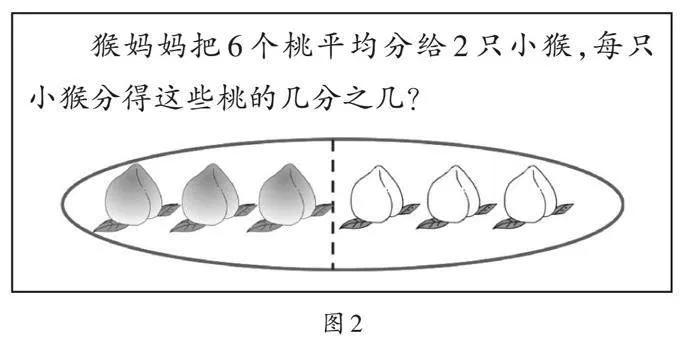
例如，笔者在教学完“认识一个整体的几分之一”后发现，仍有部分学生对分数的认识不深刻。很多时候是因为学生在第一次自主探索时产生的原生问题没有得到解决，所以笔者有意识地设置争辩的环节，帮助学生解决原生问题。笔者先出示如图2所示的问题，再引导学生进行小组合作，通过画一画、分一分表示出将6个桃子平均分给2只小猴的过程，并思考用哪一个分数表示。结果部分学生用[3/6]来表示，部分学生用[1/2]来表示。至此，课堂上的矛盾产生，争辩和质疑也随即产生。笔者充分利用这一契机，紧扣学生的原生问题进行讲解，以强化他们对知识本质内容的理解。

综上所述，在建构主义的理念下，于数学课堂中建立“质疑思维”是尤为重要的。教师需要先树立正确的教学观，并不断更新教学理念；需重视学生习得知识的原生问题，帮助学生完善知识结构；为学生提供质疑的平台，鼓励学生大胆地质疑；给学生提供分析、消化质疑的机会；将学习的主动权交给学生，使其体验质疑的乐趣和魅力。此举旨在让学生在数学学习中体会到“学起于思，思源于疑”，发展质疑问难的批判性思维，形成实事求是的科学态度，初步养成讲道理、有条理的思维品质，逐步形成理性精神。

［ 参 考 文 献 ］

[1] 吕月花.培养数学质疑能力，引导小学生深度学习[J].读与算，2021（14）：189-190.

[2] 胡梦琪.学患无疑，疑则有进：初探小学生数学质疑能力的培养方法[J].数学学习与研究，2021（5）：38-39.

（责编 梁桂广）