审辩式学习：建构“玩中学、学中悟”的数学课堂

［摘 要］在“谁先走”的教学中，基于审辩式学习的理念，设计丰富的游戏体验活动，使学生在课堂上既是“体验师”——体验公平与不公平游戏，又是“研究员”——探索常见游戏的公平性，还是“设计师”——设计公平的游戏规则。学生在“玩”的过程中能够充分感悟游戏的公平与否与事件发生的可能性是否相等有关，感悟游戏输赢与公平与否无关，发展数据意识与推理意识。

［关键词］审辩式学习；谁先走；可能性；公平性

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2024）35-0011-05

【课前思考】

孩子天生热爱游戏，正如高尔基所言：“儿童通过游戏，非常简单，非常容易地去认识这个世界。”“谁先走”这一课旨在让学生理解游戏规则的公平性，这意味着学生不仅要玩起来，还要辩起来。学生既要玩得开心，成为聚焦“学习情感”的热爱学习者；也要辩得清晰，成为聚焦“逻辑品质”的理性思维者；还要悟得透彻，成为聚焦“独立人格”的智慧决策者。

“审辩式学习”提倡在数学课堂中营造“真实、朴素、有节奏、吸引人”的情境。本课以“智力大比拼”为情境，通过使用“背对学生”的“不公平”转盘来决定参加游戏的人员，以及不公平的骰子游戏来制造冲突，为学生搭建“辩起来”的平台。随后，设计公平的骰子游戏，并利用转盘设置公平规则，让学生实际操作以检验他们是否真正“悟透彻”。

北师大版教材中的情境——决定“谁先走”的棋类游戏，既真实又有趣。教材的配图明显是中国象棋棋盘，且中国象棋有“红方先走”的规则，教材情境却未采用这一规则。于是，笔者在教学时将情境改为围棋的“谁先走”，带领学生研究围棋中“猜先”决定谁执黑子先走的公平性，展现中国传统棋类的独特魅力。

【课堂实践】

一、游戏设局，以问启学

师：老师准备邀请大家参加“智力大比拼”游戏活动。然而，由于人数限制，只能选择男生或女生参加，怎么办？

生1：可以通过玩游戏来决定。

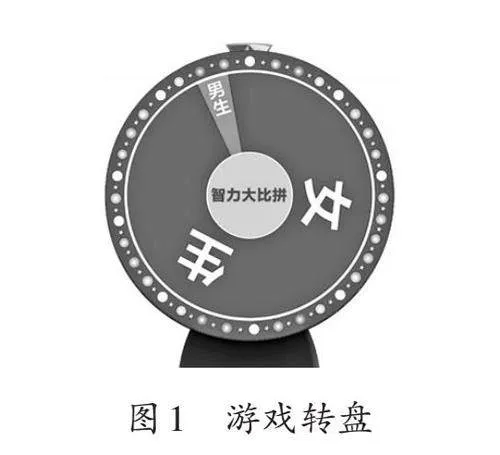
师：这主意不错！这里有一个转盘（转盘正面背对学生），上面分别标有“男生”和“女生”字样。转到谁，就派谁去。（教师转动转盘后查看结果）是女生！

（女生欢呼雀跃，男生情绪低落）

师：要不要再试一次？

男生：要！

师：好的，我们再来一次。（教师转动转盘后查看结果）还是女生！

师：看来男生不太服气，那么请一位男生来试试看。（男生上台转动转盘，教师查看结果）还是女生！

男生：不公平！

师：为什么觉得不公平？

生2：这个转盘只有“女生”吧。

生3：或者“女生”区域的面积很大。

师（向学生展示转盘正面，如图1）：现在揭晓答案。

生4：这个游戏太不公平了。“女生”的区域那么大，“男生”的区域那么小。

生5：我们应该换一个公平的转盘。

师：显然，大家都不喜欢也不愿意参与不公平的游戏。在日常生活中，我们经常接触各种游戏，什么样的游戏才算公平呢？今天我们就来探讨这个问题——游戏公平。

【设计意图：“智力大比拼”的情境营造了一个自然、真实、生动的课堂氛围；“不公平”的转盘，让学生在游戏中自然产生“不对劲”的感觉，学生自觉寻求公平的转盘，从而引出本节课的核心问题，即“什么样的游戏才是公平的”，达到以问启学的目的。】

二、慎思明辨，以探入学

师：“智力大比拼”中的围棋游戏深受大家喜爱。在围棋中，黑棋先行，那么如何决定谁执黑棋呢？

生1：我们可以抛硬币决定。

生2：或者抽签。

生3：“石头剪刀布”也行。

……

师：这些方法都可以。现在，我给大家介绍一种正式围棋比赛中决定先手的方法，叫作“猜先”。（播放视频）谁看明白了？

生4：右边的人拿一把白棋，左边的人用棋子猜他手中的白棋是双数的还是单数的。如果猜对了，左边的人就先走。

师：你们都是潜在的围棋高手。那么，你们觉得“猜先”公平吗？

生5：公平，因为任何非零自然数都可以分为双数或单数。

生6：我觉得不公平，猜错的几率似乎更大。

生7：猜对和猜错的几率是相同的，因为单数棋子和双数棋子的出现概率相等。

生8：“猜先”不是看单数棋子和双数棋子的出现几率，而是看猜的结果。

生9：可是我认为猜对和猜错的几率是相同的。假设抓的棋子是双数的，我可以猜双数或单数，一对一错；如果抓的棋子是单数的，我同样可以猜双数或单数，也是一对一错。两种情况下猜对和猜错的几率相同，所以是公平的。

生10：我要补充，总共有4种可能的结果。抓棋子的数量有单双两种情况，猜棋子数量也有单双两种情况，一共有2×2=4（种）结果，在这4种结果中，猜对和猜错各有2种，所以是公平的。

师：“猜先”的规律被你们摸透了，太了不起了。看来“猜先”确实是公平的。

师（出示图2）：除了围棋，象棋也是传统游戏中的大热门。小明和小华决定用投骰子的方式决定谁执红先走。你们觉得这个规则公平吗？

生11：公平，因为一个点数大于3，一个点数小于3。

生12：我觉得不公平。

师（出示图3）：大家的意见不一致。请小组合作操作试试，每个操作员掷两次骰子，记录员记录点数，然后小组内讨论是否公平。

生13：我们认为这个规则公平。我们组掷10次骰子，点数大于3和小于3的情况各出现了5次。

生14：我们组也是各出现了5次。我们认为这个规则是公平的。

（有不少学生举手）

师：看来有不同意见。

生15：我们组的数据是8次和2次，感觉不太公平。

生16：我们组是7次和3次，我们也觉得有失公正。

师：我们该如何判断这个规则是否公平呢？结果各不相同，该怎么办？

生17：我们可以将所有组的数据合起来看。

师：好主意。（利用电脑操作，掷骰子80次，结果显示有51次点数大于3，有29次点数小于3）看来大于3的次数确实更多。

生18：我们得考虑可能性，点数大于3有4、5、6三种情况，而小于3只有1、2两种。大于3的可能性更高。

生19：但我们组的结果为什么是5次和5次呢？

生20：可能性只是指可能发生的情况，并不意味着结果一定如此。

生21：那么，点数小于3的次数有可能超过点数大于3的次数吗？

生22：完全有可能，但这种情况发生的概率较小。

师：如果要修改规则，你们会如何调整？

生23：改为大于3和小于等于3。

生24：或者规定掷到3或6要重掷，掷到1或2就让小华先走，掷到4或5就让小明先走。

生25：我认为去掉任意两种可能性，然后将剩余四种可能性平均分配给两人，这样才公平。

师：总结得很好。

生26：我们还可以按照偶数和奇数来分配。

生27：2、3、5是质数，1、4、6不是质数，可以按照是不是质数来分。

师：在研究这两个游戏时，大家提到了一个关键词，那就是“可能性”。那么，可能性和游戏公平之间有什么联系呢？

生28：要让游戏公平，可能性必须相等！

师：原来，游戏公平的秘诀在于——

生（齐）：可能性相等！

【设计意图：通过探究“智力大比拼”情境中的游戏规则，引导学生发现游戏公平的关键在于可能性相等，学生在质疑、思考、交流、辩论中深入理解公平的概念，“因问而审，以审启思；因思生辩，以辩促辩”，学会如何调整规则以做到公平。】

三、游戏激趣，以用成学

师：有同学提到了“石头剪刀布”的游戏（师生玩三局），这个游戏公平吗？请拿出学习单，用你喜欢的方法研究。

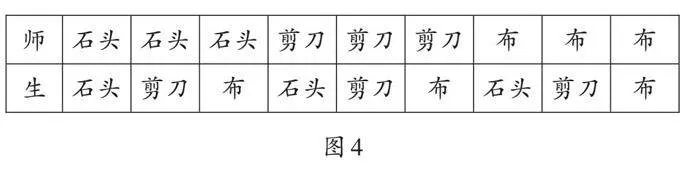
生1（出示图4）：我用表格记录，平局有3次，老师赢3次，学生赢3次，所以“石头剪刀布”是公平的。

我的记录：

师：表格清晰，论据充分！还有谁有不同方法？

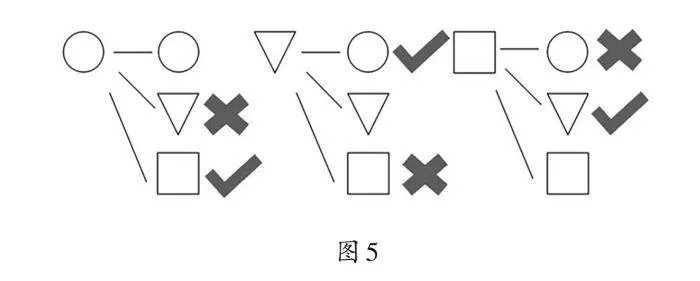
生2（出示图5）：我也认为它公平。我用圆圈代表石头，三角形代表剪刀，正方形代表布。老师出石头时，我可能平1次、赢1次、输1次；老师出剪刀和布时，结果也是三种。平局、输、赢的可能性都是相等的。

师：你的表达清楚。你用图形表示了“石头剪刀布”，简洁明了。

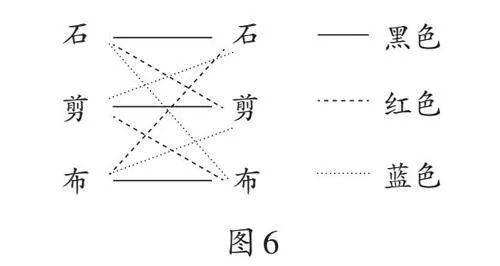
生3（出示图6）：我用连线法，共有9条线代表九种可能的结果，黑线代表平局，有3条；红线代表左边赢右边输，有3条；蓝线代表左边输右边赢，有3条。我也认为“石头剪刀布”是公平的。

师：你用不同颜色表示不同结果，直观易懂。既然游戏公平，结果可能性相等，那是不是全班同学都赢了1次、输了1次、平了1次？

生（齐）：不是。

师：这是为什么？

生4：我们发现，公平与否和结果无关，各种情况都可能发生。

师：有没有人三局都输了？（少数学生举手）明明是公平的游戏，为什么会全输？是不是作弊了？

生5：公平意味着可能性相等，但输赢是另一回事。

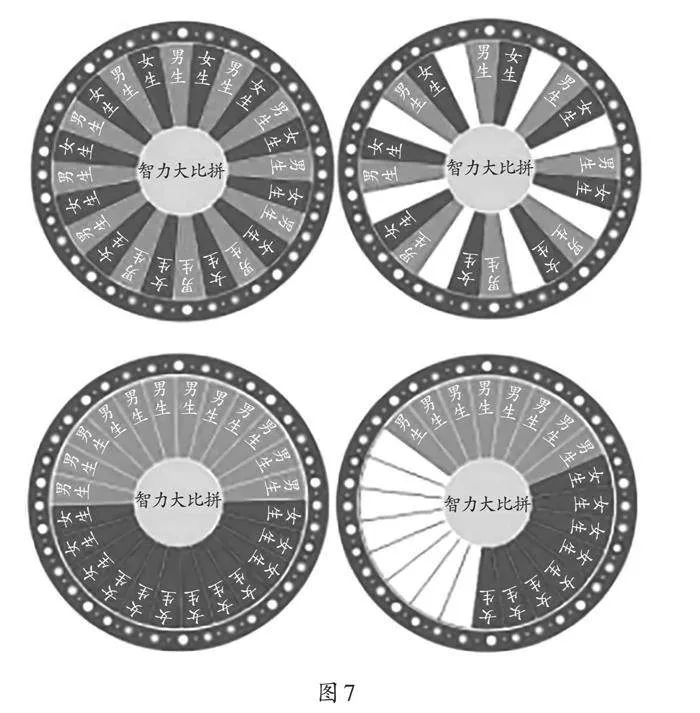
师：原来游戏的输赢和游戏是否公平没有直接关系。还记得一开始提到的“不公平”转盘吗？现在，我们来设计一个“公平”的转盘。请大家拿出设计单，用蓝色代表男生，红色代表女生，开始设计吧！

师（出示部分学生作品，如图7）：你们都是小小设计师呀！

【设计意图：“石头剪刀布”作为生活中常见的游戏，其公平性虽被大家接受，但其公平性的原理却鲜为人知。本活动旨在让学生通过喜爱的方式研究“石头剪刀布”的公平性，从而深入理解公平性与可能性相等的关系。在明确了公平性与可能性相等的概念后，进一步引导学生将这一概念应用于设计公平的转盘，通过实际操作，将理论知识转化为实践经验，不仅有助于学生思维的拓展，也使活动更具实践性和趣味性。】

四、玩中悟透，以融创学

师：现在让我们用自己设计的转盘来一决胜负，看看今天的赢家会是谁。准备，3、2、1！（全班学生的目光紧盯着转盘，不少学生兴奋地站了起来）恭喜女生获胜！

师（询问男生）：你们现在有什么感想？

生1：确实没办法，转盘是公平的，只是这次没有转到我们。

生2：是的，我们的运气不如女生。

师（转向女生）：你们有什么话想对男生说吗？

生3：不要灰心，也许下次胜利就属于你们。

师：没错，游戏总有输赢，运气也有好坏，学会接受是成长的一部分。

师：因为你们今天的表现非常出色，“智力大比拼”还为你们准备了另一个游戏——“抛瓶盖”，这个游戏是否公平？这个问题我们留到下节课再讨论。

【设计意图：学生参与自己设计的“公平”转盘游戏，能进一步体会游戏规则的公平性与实际输赢的区别。这样能引导学生在游戏中学会胜不骄、败不馁，形成公平竞争意识。这一环节也为第二课时的内容做了自然过渡，保持了教学情境的连贯性。】

【课后反思】

《义务教育数学课程标准（2022年版）》中提到：“教学活动应注重启发式，激发学生学习兴趣，引发学生积极思考，鼓励学生质疑问难，引导学生在真实情境中发现问题和提出问题，利用观察、猜测、实验、计算、推理、验证、数据分析、直观想象等方法分析问题和解决问题。”本节课通过一个个数学趣味活动让学生成为热爱学习者、理性思维者与智慧决策者。

首先，培养“快乐学习”、聚焦“学习情感”的热爱学习者。

快乐学习是激发学生热情和动力的关键。本节课通过营造轻松愉快的学习氛围，让学生在游戏中体验学习的乐趣，从而培养热爱学习的学生。

课堂上，学生沉浸在充满乐趣的游戏中。课前，以“激发矛盾”的游戏吸引学生注意力，同时激发学生的好奇心。通过非常规的转盘游戏，学生发现女生连续获胜的不公平现象，开始了对游戏“公平性”的探讨。课中，学生参与小组合作的掷骰子游戏，探讨“大于3”与“小于3”规则的公平性，以及经典游戏剪刀石头布的公平性。这样，学生在多样化的游戏和真实情境中快乐学习。

其次，培养“勇于思辨”、聚焦“逻辑品质”的理性思维者。

勇于思辨是理性思维的表现之一。本节课鼓励学生深入思考和辩论，以提升逻辑品质。

课堂上，学生的思辨清晰有序。教材中的象棋先走问题与实际比赛规定不符，因此笔者引导学生研究围棋“执黑先走”的公平性。在“猜先”公平性的探讨中，学生提出单双数的公平性观点，并展开深入讨论，最终达成共识。这一过程不仅锻炼了学生的思维，也培养了学生尊重他人观点、理解他人想法的合作精神和沟通能力。

最后，培养“博学明德”、聚焦“独立人格”的智慧决策者。

博学明德是积极的学习品质，有助于学生积累知识、提升道德素养和智慧决策力。

在本节课中，学生深刻领悟到游戏的输赢与运气好坏并存。教师通过游戏引导学生思考：为何游戏设计公平，结果却不平均？学生意识到，公平的关键在于结果的可能性相等，而实际输赢则是另一回事，从而树立了公平公正的意识。

课末，教师带领学生回到趣味情境，用学生设计的公平转盘再次开展游戏。这次，男生虽然输了但态度良好，女生赢而不骄，反而安慰男生。这样，面对未来更多游戏的输赢，学生将拥有智慧决策与平和心态。

“快乐学习”“勇于思辨”与“博学明德”三者相辅相成，审辩式学习将它们有机结合，有序展现。本节课不仅培养了学生的数据意识与应用能力，落实了核心素养，更实现了学生思维与品质的全面发展。

［ 参 考 文 献 ］

[1] 穆传慧.总结经验：审辩式学习的高贵品质[J].小学教学，2021（6）：18-19.

[2] 穆传慧.审辩式学习：价值、内涵与基本环节[J].小学教学参考，2023（8）：1-6.

[3] 穆传慧.审辩式思维：审辩式学习的中国逻辑表达[J].小学教学参考，2023（11）：1-5.

[4] 穆传慧.审辩式学习：学与教的深度对话[J].小学教学参考，2023（20）：1-3，8.

【本文系深圳市教育科学2023年度规划成果培育课题“审辩笃学，明德成人：审辩式学习33年实践探索”（课题编号：cgpy23004）及罗湖区“十四五”规划年度专项课题“小初高贯通培养拔尖创新人才的数学课程建设实践研究”（课题编号：LHZXGT-2416）的阶段性成果。】

（责编 金 铃）