审辩式学习：深化意义建构

［摘 要］审辩式学习的基本环节包括“问学（以问启学）、探学（以探入学）、辩学（以辩立学）、用学（以用成学）、融学（以融创学）”。文章以“间隔排列（探索规律）”一课为例，论述将“五学”课堂作为学习路径，运用“观察”“猜想”“验证”“概括”“转化”等方法，鼓励学生积极、自主、理性地开展分析、比较、推理和评价等认知活动，引导学生在审辩式学习中发展审辩思维与合作探究能力，以形成良好的学习品质和人格气度。

［关键词］审辩式学习；意义建构；“五学”课堂；转化思想

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2024）35-0006-05

【教学内容】苏教版教材三年级上册“间隔排列（探索规律）”。

【教学目标】

目标1.开展合作探究活动，找到“两种物体排成一行，两端相同时，两端物体的数量比另一种物体的数量多1；两种物体排成一行，两端不同时，它们的数量正好相等”这一规律。

目标2.经历探索规律的过程，掌握观察、分析、比较、归纳等数学方法，概括并利用发现的规律解决实际问题，提升审辩式思维与合作探究能力。

目标3.在解决实际问题的过程中感受方法与策略的多样性，体验数学思考与探究的乐趣，形成积极的数学学习情感，形成良好的学习品质。

【教学重点】经历间隔排列规律的探索过程，找到规律“两种物体排成一行，两端相同时，两端物体的数量比另一种物体多1；两种物体排成一行，两端不同时，它们的数量正好相等”。

【教学难点】能够采用恰当的学习方式，并准确地表达所找到的规律。

【教学准备】多媒体课件；正方形与三角形磁性贴片每组各10枚；研学单50张。

【教学过程】

一、课前预学

师：同学们看过电视剧《西游记》吗？这部影片中的四个主人公是谁？猜猜看，我最喜欢的是哪一位呢？（猜测略）其实，我最喜欢的是猪八戒。你们再猜猜，我为什么最喜欢猪八戒呢？

师：大家想一想，唐僧师徒四人中，谁最幽默风趣？

生（齐）：猪八戒。

师：大家在回答问题时不仅使用了观察的方法，还运用了猜想的方法。其实，观察与猜想是我们必须具备的两项技能。今天就比一比，看看谁的观察力和猜想能力最强！

【思考】课前交流是课堂教学的有机组成部分，它能有效缓解学生压力、渗透学习方法，帮助学生迅速进入特定的学习情境，并促进师生关系的融洽，为上好一堂课奠定坚实的基础。因此，课前交流是教师借班上课必不可少的环节。

二、课中共学

（一）创设情境，以问启学

1.猜图游戏，初步认识间隔排列

师：请看大屏幕（出示1个圆），这是什么图形？现在呢？（出示1个五角星）这个又是什么图形？（再出示1个圆）再看看是什么？（继续出示1个五角星）（如图1）猜猜看，下一个会是什么图形？接下来会怎样？（学生回答略）

师：你们猜对了！为什么能猜得这么准？

生1：我发现这是有规律的——一个圆后跟一个五角星，如此循环排列。

师：实际上，这种依次排列，一个接着一个的，被称为“一一间隔”。这样的排列方式叫作“间隔排列”。一个圆对应一个五角星（如图2），我们就说这两种图形是一一对应的。

2.联系生活，深入认识间隔排列

师：在日常生活中，你们见过一一间隔排列的现象吗？谁能举例说明？

师：我也收集了一些一一间隔排列的案例，请大家看大屏幕（播放生活中的间隔排列现象）。这种排列使物体看起来井然有序，给人一种美的感受。

【思考】学生在理解“一一间隔”概念时往往感到困难，因为生活中的“间隔排列”现象多种多样，如三种或更多种物体的排列等。笔者设计的猜图游戏虽然简单，却有效地提供了间隔排列的典型实例，促进学生通过“一个一个”到“一个隔着一个”，再到“一一间隔”和“间隔排列”的理解，逐步构建起相关概念。由于实例数量和类型有限，笔者又引导学生列举、交流和欣赏更多生活中的间隔排列现象，体现规律的普遍性和数学与生活的联系，以加深学生对“间隔排列”的理解。

（二）操作验证，以探入学

1.操作活动（教师为每个学习小组准备正方形与三角形磁性贴片各10枚）

师：请大家用4个正方形和4个三角形摆一排，形成一一间隔的排列。

生1：□▲□▲□▲□▲。

生2：▲□▲□▲□▲□。

师：请用4个正方形和5个三角形摆一排，也形成一一间隔的排列。

生3：▲□▲□▲□▲□▲。

师：第一个位置可以放正方形吗？

生（齐）：不可以，只能先放三角形，否则正方形就不够用了。

师：正如大家所说，一端是正方形，另一端是三角形。这种情况我们称之为两端物体不同，这时两种物体的数量相等。若两端都是三角形，我们称之为两端物体相同，这时两种物体的数量不等。

2.拓展活动

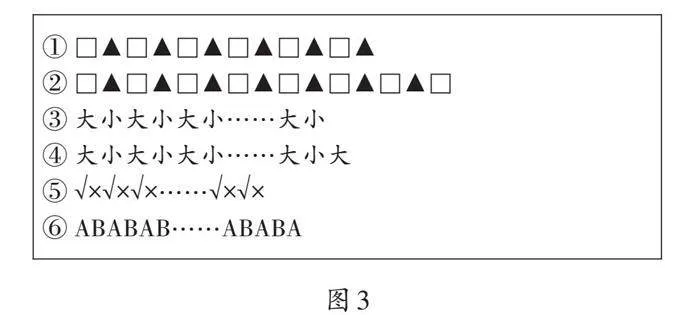
师（出示图3）：请观察这几组图形、文字、符号或字母，它们都是一一间隔排列的。第①组两端的元素相同吗？哪种更多？（电脑演示一一对应过程）

师：第②组两端的元素相同吗？哪种更多？

师：在第③组中，中间的省略号表示什么？现在还能用数的方法解决吗？哪种物体更多？

师：根据两端物体相同或不同，你有什么新发现？

生4：两端物体相同时，两种物体数量不等；两端物体不同时，两种物体数量相等。

师：你观察得很仔细，发现了这种排列的主要特点。下面我们一起去小兔子乐园看看。

【思考】学生通过对比不同素材，不断深化对两种物体间隔排列的理解。笔者有意设置认知障碍，制造思维冲突，引出两端相同的一一间隔排列，让学生明白这一类型是本节课的学习重点。这不但为学生发现、总结、提炼规律奠定了基础，而且帮助他们将生活中的排列原型抽象为数学层面的间隔排列模型。此外，当学生习惯用“数”的方法比较数量后，笔者引导学生思考含有省略号的排列，促使学生运用新学的规律解决问题，自然地将关注点转向“两端”，使得学生在思维冲突中加深对规律的理解。

（三）交流反思，以辩立学

1.自主探究

师（出示图4）：图中哪些物体是一一间隔排列的？

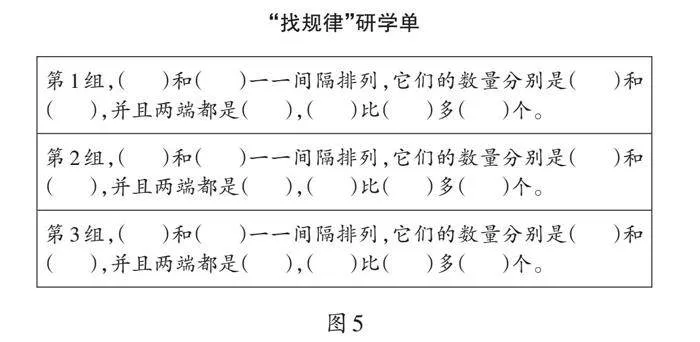
师：这些一一间隔排列有什么共同的规律？观察这几组一一间隔排列，自主探究，完成研学单（如图5）。

“找规律”研学单

2.概括规律

师：在这种一一间隔排列中，两端物体的数量与另一种物体的数量之间存在怎样的关系？请尝试用自己的话来总结。

生5：在两端物体相同的一一间隔排列中，两端物体的数量比另一种物体的数量多“1”。

师：大家对这个结论有什么看法？有没有不同的意见？

【思考】为了有效引导学生自主探究，笔者首先让学生观察主题图，寻找符合一一间隔排列的实例，并对其分组、编号。在“研学单”中特别设计了填写每组两种物体的对应数量，帮助学生发现“多1”这一关键共性。在探究过程中，即使学生的总结不够全面，未能精确捕捉排列的共同规律，教师也应给予鼓励性评价，并提供充足的思考时间和空间，促使学生积极参与数学活动，获得丰富的数学体验。

（四）解决问题，以用成学

1.基本练习

（1）20只兔子站成一排，相邻两只兔子中间有一朵蘑菇，一共有多少朵蘑菇？如果有100只、1000只兔子，又有什么规律呢？

（2）把20块手帕像图4那样夹在绳子上，一共需要多少个夹子？如果有100块手帕呢？1000块手帕呢？

2.变式练习

（1）①②①②①②①②①②……①②，则（ ）。

A.①和②的数量同样多 B.①的数量多

C.②的数量多

（2）

两端的物体是（ ），另一种物体是（ ），（ ）的数量比（ ）的数量多1。

（3）看结尾说出开始的图形是什么。

①如果两种颜色的圆个数相等，那么开头的是（ ）色的圆。

②如果黑色的圆个数比灰色的圆的多1个，那么开头的是（ ）色的圆。

3.开放练习

师：如果把我的照片和猪八戒的照片一一间隔排列，已知我的照片用了4张，那么猪八戒的照片用了多少张？

师：我听到了几种不同的答案。谁能解释清楚？（教师边听学生叙述，边用课件展示图形排列，如图6所示）

【思考】本环节的练习题既展现了知识的层次性，又促进了学生思维的全面发展。首先，通过基本练习引导学生发现解决问题不是简单地“加1”或“减1”，而应仔细分析条件和问题，这样的处理既形象又直观，深化了学生对规律的理解；其次，变式练习不仅检验了学生对新知识的掌握程度，还帮助学生巩固和拓展了对一一间隔排列规律的认识，特别是逆向思维题目的设计，有效提升了学生的认知水平，打破了学生的思维定式；最后，兼顾了不同学习能力的学生，设计的开放性问题不但有助于他们有效地整理学习内容，而且与课前交流的内容相呼应，实现了教学的首尾呼应。

（五）融会贯通，以融创学

师：本节课我们学习了什么？你有哪些收获？（生答略）

师：我们探讨了物体一一间隔排列的规律。当两种物体间隔排列成一行，且两端物体相同时，这种物体的数量比另一种物体的数量多一个。这种现象在生活中很常见，它让物体的排列显得有序，展现出独特的秩序美。

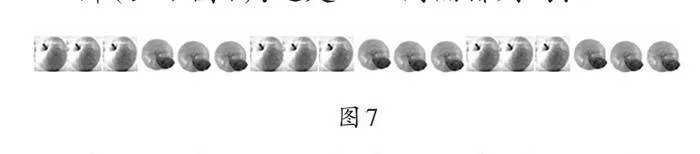
师（出示图7）：这是一一间隔排列吗？

生6：不是，这是3个苹果接着3个橘子排列，不属于一一间隔。

生7：我认为这是三三间隔排列。

师：你的想法很有创意。

生8：能不能将它看作一组一组的间隔排列？

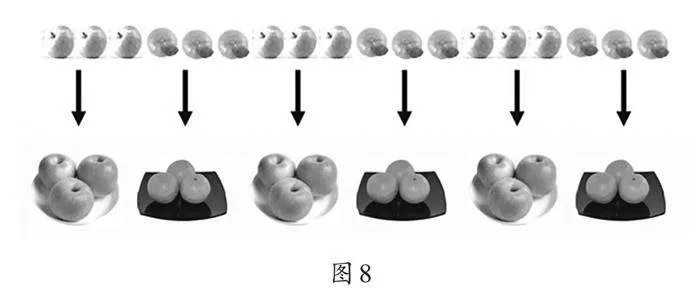
师（出示图8）：好思路！我们可以将“单摆”转化为“盘装”，这就是一一间隔排列的奇妙之处。生活中，不同的视角往往带来不同的发现和结论。

师：这节课我们研究的是排成一行的间隔排列，如果两种物体一一间隔排列成一个圆，它们的数量关系又是怎样的呢？这个问题留给大家课后思考。

【思考】本环节旨在帮助学生整理知识，优化知识结构。通过“峰回路转”的题目，引导学生深入思考“是”与“不是”的区别，展示从不同角度看待问题的价值。同时，鼓励学生探索新规律，提出新想法，体现数学学习的科学价值。最后，以开放性问题结束，让学生带着新的问题走出教室，体现了不上“打句号”的课，将学习活动由课内引向广阔的课外，这也是审辩式学习倡导的教学理念之一。

【课后反思】

审辩式学习强调学科育人的核心价值，倡导问题导向的学习方法，鼓励学习者通过自问和互问，在个体探索和小组合作中发现、验证，进而形成理性思维和科学精神。正如特级教师穆传慧所描述：“审辩式学习能让学习者在探索中产生感悟、在对话中放飞思维、在审辩中建构意义、在扬弃中总结经验、在实践中智慧决策、在自由中走向创造、在发展中自我实现。”

本课较好地体现了“问学（以问启学）、探学（以探入学）、辩学（以辩立学）、用学（以用成学）、融学（以融创学）”的“五学”课堂特色，让审辩式学习教学理念落地生根。

一是学习素材整合巧妙。新课程理念强调因地制宜、因人制宜、因时制宜地“活化”教材，提升其趣味性和生动性。有观点认为“一盘好菜=好的原料+好的式样+好的厨艺”，那么“一节好课=好的学习内容+好的呈现方式+好的学习方法”。在本节课中，笔者将教材与生活资源融合，以猜图游戏引导学生深入理解“间隔排列”的概念；通过学习材料的变式、拓展和创新处理，逐步加深学生对知识的理解；在“以用成学”的练习环节，设计的开放练习强化了教学重点，增强了趣味性和创造性，有效激发了学生的学习兴趣和探究欲；课末的“峰回路转”环节巧妙融入转化思想，令人回味无穷，也取得了较好的育人效果。

二是学习过程展示细腻。审辩式学习强调重视数学课程的人文价值，发挥其育人作用。数学不仅是工具，也是一种文化，教师应挖掘其中的人文元素，让学生在学习中接受熏陶和教育，使课堂成为知识传递和人性培养的场所。本节课的设计细腻且层次丰富，从“课前交流”的自然引导，到“课中共学”的情境设置、问题探讨、操作启发、交流研讨、抽象总结，再到课末“以融创学”环节的巧妙转折和留白，课程既突出了认知重点，又融入了审辩思维，充分体现了“学生才是学习的主人”的教学理念。

三是学习节奏张弛有度。审辩式学习是一种注重学生个性与心理的数学学习方式，旨在通过精心设计的数学问题激发学生的思考欲望，鼓励学生自主探索、合作研究、质疑反思。教师需多角度呈现问题，引发学生的兴趣，刺激学生的兴奋点，使其置身情境中分析解决问题，实现认知结构的构建与完善。本节课有效地引导学生经历了从“生活原型”到“建立数学模型”，再到“解释与应用模型”的学习过程，教学节奏适中，张弛有度。学生通过猜测、验证、讨论等活动，积极探索未知领域，不仅理解和掌握了数学知识，还积累了丰富的数学活动经验，为终身学习和个人发展奠定了坚实基础。

总之，审辩式学习立足学生个体需求和学习认知规律，重视整合教学资源，不断深化知识的意义建构，进而发展学生的审辩式思维与合作探究能力，塑造学生优良的学习品质与人格特质。秉承审辩式学习理念，必能打造目标多元、立意深远、结构精致、过程丰富的数学课堂。

［ 参 考 文 献 ］

[1] 穆传慧.审辩式学习：价值、内涵与基本环节[J].小学教学参考，2023（8）：1-6.

[2] 穆传慧.审辩式思维：审辩式学习的中国逻辑表达[J].小学教学参考，2023（11）：1-5.

[3] 穆传慧.审辩式学习：学与教的深度对话[J].小学教学参考，2023（20）：1-3，8.

（责编 金 铃）