Matlab 软件辅助“误差理论与数据处理”课程教学实践

摘要：“误差理论与数据处理”是测控技术与仪器专业的核心课程，构成了重要的知识和实践基础。针对“误差理论与数据处理”课程教学时数有限、概念繁多以及公式推导和计算复杂等问题，本文将课程教学案例转化为Matlab算例，以帮助学生更好地理解相关概念和公式。以工程中广泛应用的最小二乘为典型案例，展示了Matlab软件在该课程辅助教学中的有效性。此外，Matlab的辅助教学显著提升了学生的学习兴趣和自学能力。

关键词： 误差理论与数据处理；辅助教学；Matlab软件；最小二乘；课程实践

中图分类号：G642 文献标识码：A

文章编号：1009-3044（2024）32-0179-02 开放科学（资源服务）标识码（OSID） ：

0 引言

“误差理论与数据处理”课程是测控技术与仪器等专业的必修核心课程，课程内容按误差理论和数据处理两个模块进行组织。主要内容包括误差的基本性质与处理、误差的合成与分配、线性测量的参数最小二乘法处理以及回归分析等。通过本课程的学习，学生应掌握误差的基本概念，不同性质误差的变化规律及处理方法；权的概念及不等精度测量的数据处理方法，误差的合成与分配，回归分析等。

然而，在“误差理论与数据处理”课程的教学中，学生常常难以理解基本概念，且课程中涉及大量公式推导，这要求学生具备扎实的高等数学、线性代数、概率论与数理统计等基础知识，以便更好地理解这些公式。又由于“误差理论与数据处理”课程学时只有32 学时，学生很难有时间回顾推导公式过程中用到的数理统计等课程知识，也不能很好地理解该课程的概念、相关公式和花费较多时间计算问题，这使得部分学生学习兴趣不高，从而影响课程学习[1]。

针对“误差理论与数据处理”课程教学中面临的问题，本文通过Matlab软件辅助教学，旨在简化基本概念的讲解和计算过程，提高计算效率，帮助学生理解课程中的复杂计算问题。下面通过工程中广泛使用的最小二乘为例展示采用Matlab软件把“误差理论与数据处理”概念和公式转化为软件算例，进行课程辅助学习，提高教学效果。

1 Matlab 软件简介

Matlab软件作为一种数学计算工具，已广泛应用于工程和科学计算等多个领域，并成为国内外工科学生的必修或选修课程，适合用于“误差理论与数据处理”课程的辅助教学。测控技术与仪器专业的学生通过学习Matlab软件，不仅能够加深对基本理论知识的理解、还能增强数学应用能力和学习兴趣，这对培养学生在光机电一体化领域的发展具有积极意义。另外Matlab具有显著的优势，如用户友好、直观的编程语法、用于各种数值分析的高质量数值算法、强大而易使用的图形、执行计算所需的简单命令语法以及许多附加组件工具箱、实数和复数矢量矩阵[2-3]。

由于简洁的Matlab软件代码和形象的图形表示，节省大量计算时间，学生通过软件计算结果与理论公式结果比较，直观理解课程知识[4]。

2 基于Matlab 软件的最小二乘教学案例

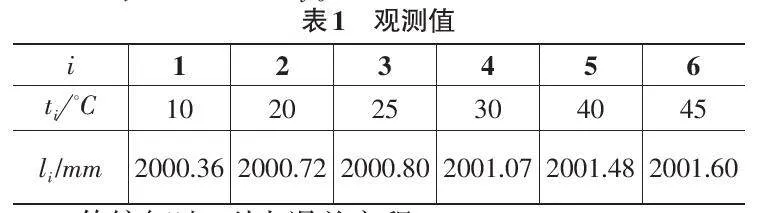
下面通过实例说明Matlab在“误差理论与数据处理”课程教学中的应用。例：已知任意温度t 时的铜棒长度yt、0℃时的铜棒长度y0 和铜的线膨胀系数α 具有线性关系yt = y0 （1 + αt）。现测得在不同温度t 下，铜棒长度li见表1，估计y0和α 的最可信赖值[5]。

传统解法：列出误差方程

vi = li - y0 （1 + αti ） ， （i = 1，2，...，6） （1）

式（1） 中，li 为在温度ti 下铜棒长度的测得值；α 为铜的线膨胀系数。

令y0 = α， αy0 = b 为两个待估计参量，则误差方程可写为

vi = li - （a + ti b） ， （i = 1，2，...，6） （2）

为了计算方便，数据列表如表2所示。

基金项目：测控技术与仪器专业“12N 品牌专业”建设工程项目省级专业；“十四五”江苏省高等学校重点教材建设项目（2021-2-172）