波浪作用下单桩周围海床孔压和液化响应数值研究

摘" 要： 基于RANS方程和u-p形式的比奥固结方程建立波浪—单桩—海床的耦合模型，讨论了桩周海床两类孔压响应分布及相应液化发展特点.通过与物理模型试验数据、解析值和数值结果对比，验证模型的准确性.在此基础上，研究了单桩周围海床中瞬态孔压和累积孔压的分布以及相应的液化发展特征.结果表明：桩前土体的累积孔压可达到瞬态孔压幅值的144倍，累积孔压占主导的区域处于桩周距土表0～4""" m，并随波浪作用时间增加而向下扩大；瞬态孔压占主导的区域处于桩周距土表4～20 m，并随土体剪切模量的减小而缩小；随着土体饱和度、渗透系数和剪切模量减小，累积孔压相对瞬态孔压幅值的比值增大，桩周土体最大瞬态液化深度增加；桩周土体最大综合液化深度受土体剪切模量和渗透系数影响显著，并表现出振荡特性；水平向渗透系数对土体液化深度影响微弱.研究结果有助于进一步评估单桩周围海床的液化灾害.

关键词： 波浪模拟；比奥固结方程；瞬态孔压；累积孔压

中图分类号：P75;TU470""" 文献标志码：A""""" 文章编号：1673-4807（2024）05-009-08

DOI：10.20061/j.issn.1673-4807.2024.05.002

收稿日期： 2023-03-23""" 修回日期： 2021-04-29

基金项目： 国家自然科学基金面上项目（51879133）

作者简介： 邓温妮（1985—），女，博士，副教授，研究方向为环境岩土工程和海洋岩土工程. E-mail： wdeng@seu.edu.cn

引文格式： 邓温妮，葛玮堃.波浪作用下单桩周围海床孔压和液化响应数值研究［J］.江苏科技大学学报（自然科学版），202 38（5）：9-16.DOI：10.20061/j.issn.1673-4807.2024.05.002.

Numerical study on pore pressure and liquefaction responseof seabed around monopile under wave load

DENG Wenni， GE Weikun

（School of Civil Engineering，Southeast University，Nanjing 211189， China）

Abstract：Based on RANS equation and Biot consolidation equation of u-p form， a coupled wave-monopile-seabed model is proposed to discuss the distribution of two types of pore pressure response and corresponding liquefaction development. The accuracy of this model is verified by comparing results with physical model test， analytical and numerical solutions. On this basis， the distribution of transient and cumulative pore pressure in the seabed around a single pile and the corresponding characteristics of liquefaction development are discussed. The results show that the cumulative pore pressure of soil in front of the monopile could reach 144 times the amplitude of transient pore pressure. The region dominated by the cumulative pore pressure is located in the range of 0～4 m from seabed surface around monopile and continuously develops downwards with the time of wave load increasing. The region dominated by transient pore pressure is located in the range of 4～16 m from seabed surface around monopile and shrinks with the decrease of soil shear modulus. With the decrease of soil saturation， permeability coefficient and shear modulus， the ratio of cumulative pore pressure to transient pore pressure amplitude increases， and the maximum transient liquefaction depth around monopile increases. The maximum integrated liquefaction depth around monopile is significantly influenced by shear modulus and permeability coefficient of soil and shows oscillatory characteristics. Horizontal permeability has limited effect on liquefaction depth. This study helps to further assess liquefaction hazards of seabed around monopile.

Key words：wave simulation， Biot consolidation equation， transient pore pressure， cumulative pore pressure

在复杂多变的海洋环境中，土体液化常常是导致上部结构失稳的重要原因，而土体的孔压响应是检测或评估该灾害的重要依据.在波浪循环作用下，海床土体内将产生超静孔压；当土体内某处的超静孔压等于有效应力时，液化即发生.波浪导致的海床响应可根据产生机理的不同，分为瞬态响应和累积响应.其中，瞬态响应是有关土体应力-应变和孔压的准静态解答，忽略了波浪荷载加载时长和路径对土体应变的影响；累积响应是在此基础上，考虑土体受波浪循环剪切作用后产生的塑性变形与累积孔压的解答.近年来，国内外诸多学者对两类响应进行了大量研究.在瞬态响应方面，基于比奥固结方程和储水方程，文献［1-2］分别给出了无限和有限海床在行进波下的瞬态响应解析解.文献［3-4］将解析解的应用范围扩展至复杂波浪条件下的各向异性和非均质土体.文献［5］研究了单桩嵌入海床深度对海床瞬态液化的影响机理.文献［6］将波浪条件扩展至非线性波浪，研究了管桩基础周围海床的液化响应.最近，文献［7］实现海床和波浪模型间的双向耦合，完善了海床的瞬态响应研究.在累积响应方面，文献［8］推导了基于剪应力比的一维累积孔压模型.文献［9］简化了该模型，推导了累积孔压的解析解，并通过实验验证其有效性.文献［10-11］将该模型扩展至二维和三维，并应用到防波堤-海床和三维单桩-海床的累积孔压研究中.

在波浪作用下，单桩周围海床各处存在不同程度的瞬态和累积孔压.海床土体性质不同，两类孔压响应的分布及相应液化的发展特征也不同.已有文献大都侧重于某一类孔压响应的研究，缺少对两种孔压分布及相应液化特点的讨论.文中采用RANS方程和k-ε湍流模型建立波浪-单桩模型，选择u-p形式的比奥多孔介质动力方程建立单桩-海床模型，通过模型间单向耦合，分析单桩周围海床两类孔压的分布特点，讨论土体参数对两类孔压分布的影响，并进一步给出单桩周围海床的液化发展规律.

1" 数值模型

采用推板式造波法进行造波，数值水槽两侧设置一定长度的浮式防波堤作为消波段［12］，通过求解RANS方程建立波浪—单桩模型；通过求解u-p形式的比奥固结方程建立单桩—海床模型，并采用单向耦合方法实现子模型数据转递.模型尺寸设置如图 其中：L为波长；Rp为单桩半径.

1.1" 波浪模型

对于无源不可压流体，RANS方程为：

uixi=0（1）

uit+uiujxj=-1ρfpxi+xjμuixj+ujxi+

xj（-ρfu′iu′j）+gi（2）

式中：ui、p分别为笛卡尔坐标系下流体单元位移和流体压力的时均分量；ρf为水的密度；gi为加速度分量；μ为流体的动力粘度；-ρfu′iu′j为雷诺应力项：

-ρfu′iu′j=μtuixj+ujxi-23ρfδijk（3）

标准k-ε模型方程：

kt+ujkxj=1ρf·xjμ+μtσkkxj+Pk-εk（4）

εkt+ujεkxj=1ρf·xjμ+μtσsεkxj+εkkCs1Pκ-Cs2εk（5）

式中：μt=ρfCμk2εk；δij为克罗内克符号；k为流体的湍动能；Pk为湍动能的生成项，可以流体速度梯度表出；εk为湍动能耗散率；Cμ、σk、σs、Cs1和Cs2为模型常数，分别取0.09、1.00、1.30、1.44和1.92.

造波板位移表达式为：

Um=t2T·Sw2ωcos （kwx0-ωt）" t≤2T

Sw2ωcos （kwx0-ωt）tgt;2T（6）

HSw=4（cosh （kwh））2-1sinh （2kwh）+2kwh（7）

式中：T为波浪周期；Sw为造波板冲程；ω为波浪角频率；kw为波数；H为波高；h为水深；x0为造波板中心坐标.

1.2" 单桩-海床模型

1.2.1" 瞬态响应模型

采用u-p形式的比奥多孔弹性固结方程，方程如式（8、9）.该模型方程考虑了土骨架单元的加速度并忽略了孔隙水相对于土骨架单元的加速度.文献［13］先后指出在低渗透性海床中，孔隙水的加速度不明显，因而对应的加速度项对方程的贡献很小，而u-p模型能够减少建模的复杂度并能提供足够的精确性.

KxKz2Px2+KyKz2Py2+2Pz2-γwnβKzPt+ρf2εst2=γwKzεst（8）

σsij，j+ρgi=ρu¨i（9）

式中：P为波浪动压力引起的瞬态孔压；n为土的孔隙率；Ki为土体i方向的渗透系数；γw为水的重度，10 kN/m3；β为孔隙水的压缩系数；εs为土体体应变；ρ为土的平均密度，ρ=（1-n）ρs+nρf，ρs为土体密度.

1.2.2" 累积响应模型

累积孔压的控制方程为：

prt=cvx2prx2+cvy2pry2+cvz2prz2+σ′0Tτinsαrσ′0-1βr（10）

式中：pr为海床土体的累积孔压；Cvi=KiE3（1-2μ）γw，为土体各向固结系数；σ′0为考虑土体在单桩作用后的固结应力；αr=0.34Dr+0.08 βr=0.37Dr-0.4 为模型经验系数，Dr为土的相对密度；τins为采用土体剪应力的相位分辨值［13］.采用文献［11］提出的表达式：τins=τ2xz+τ2yz+τ2xy，其中τij为每一时间步中的瞬时剪应力分量.

2" 模型验证

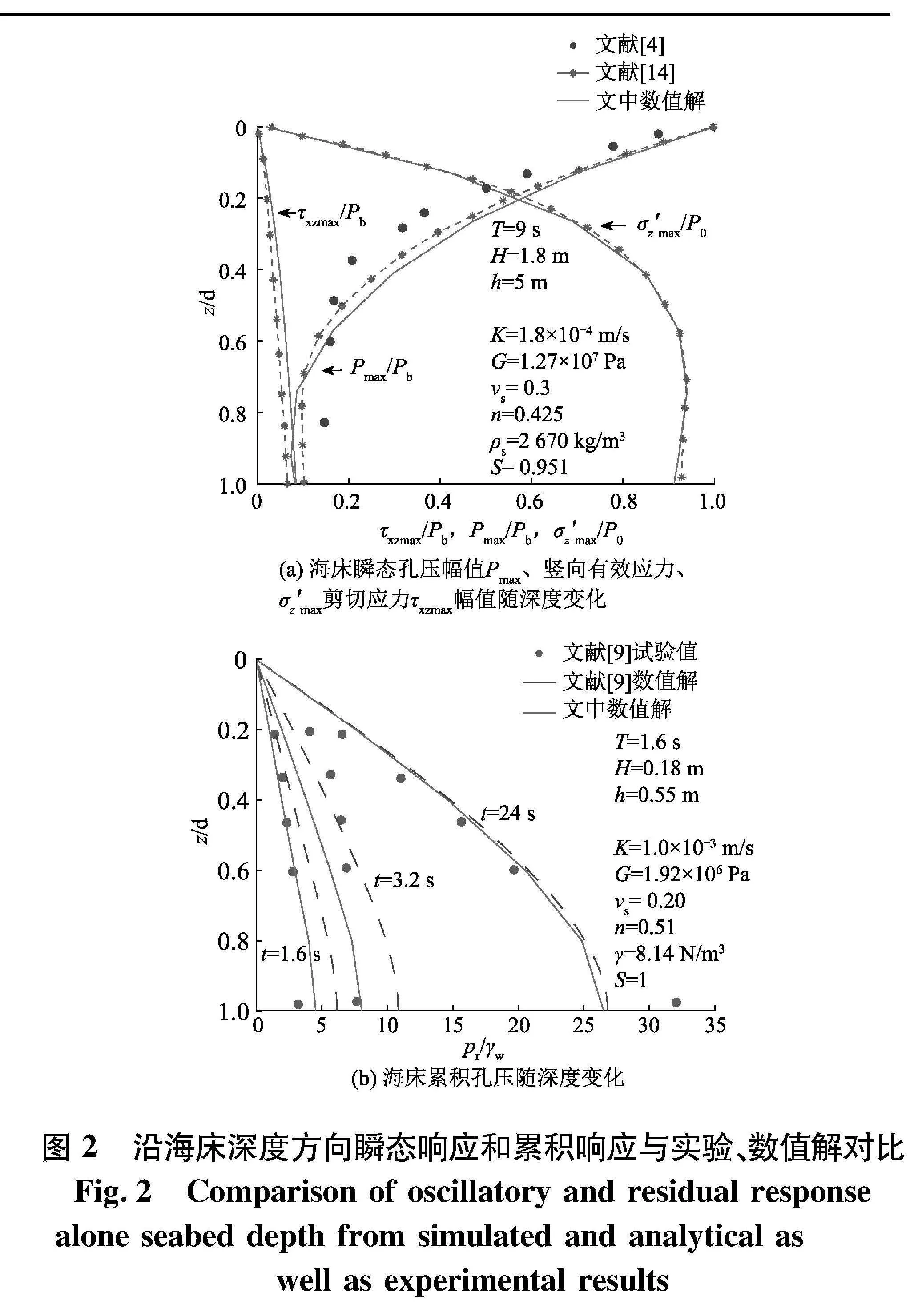
文献［4］关于土体应力和孔压响应的解析解及文献［14］中模型试验数据对比，具体参数如图2（a）.图中：z为土体深度;d为海床的厚度.可以发现，土体瞬态响应的数值解能与解析、试验结果较好吻合；参照文献［9］的模型试验，具体参数如图2（b）.可以发现，土体的累积孔压与试验结果较好吻合.通过对比模型结果与试验数据、解析值和数值解，验证了模型的有效性.

3" 单桩周围海床两类孔压响应与液化分析

在模型验证的基础上，进一步对波浪作用下单桩周围海床两类孔压的分布特征及相应的液化响应进行分析.文献［15］对我国福建省近海波浪参数特征进行了分析，发现该区域波浪的平均周期和有效波高分别处于2～10 s和0～4"" m.此外，近海海

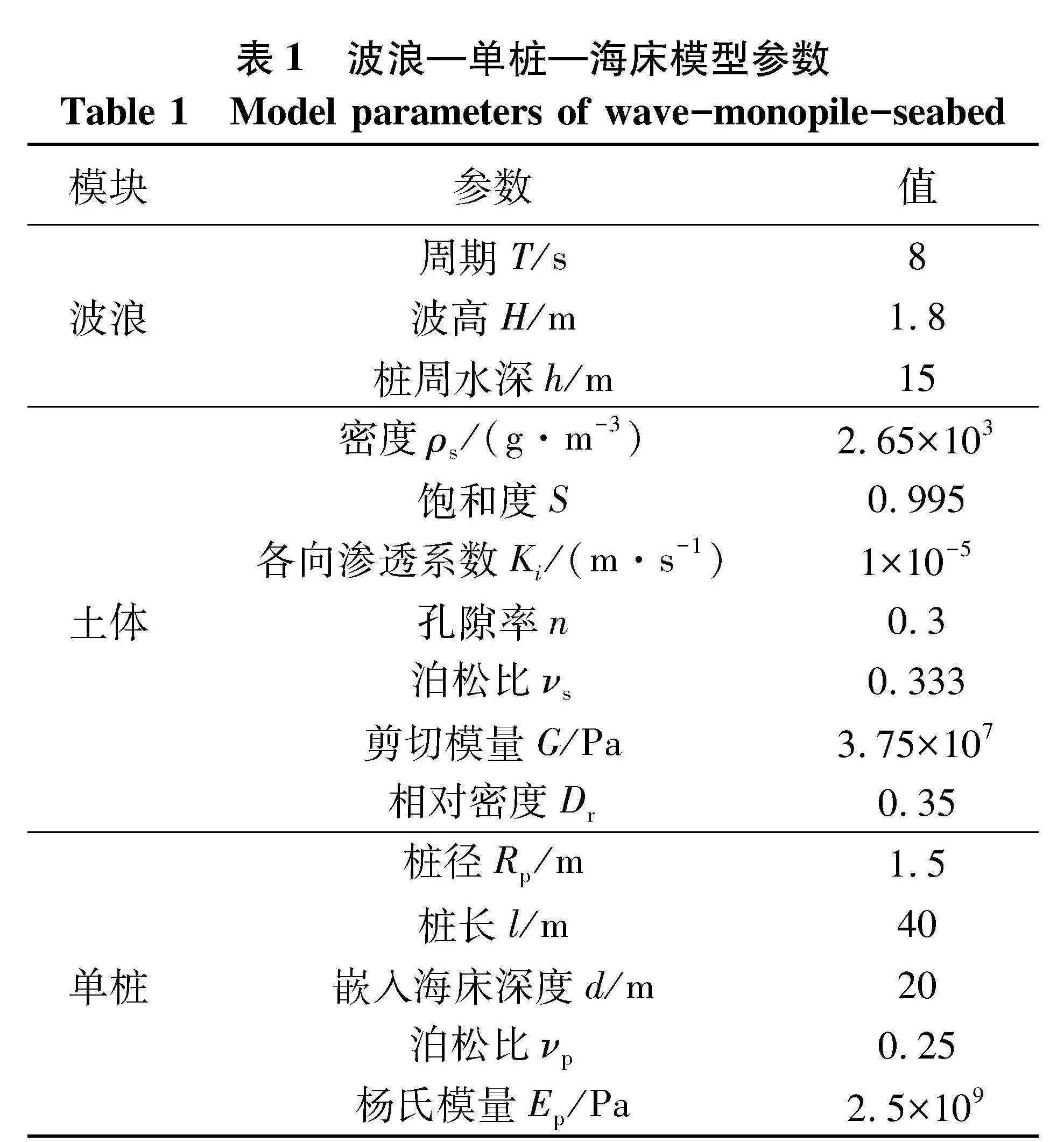
床表层土体大多为砂土、土和淤泥质土，土力学参数分布广泛，文中选择文献［16］的一维圆筒试验和文献［17］的离心模型试验土体参数作为参照.波浪、海床土体和单桩的相关参数见表1.

3.1" 孔压响应

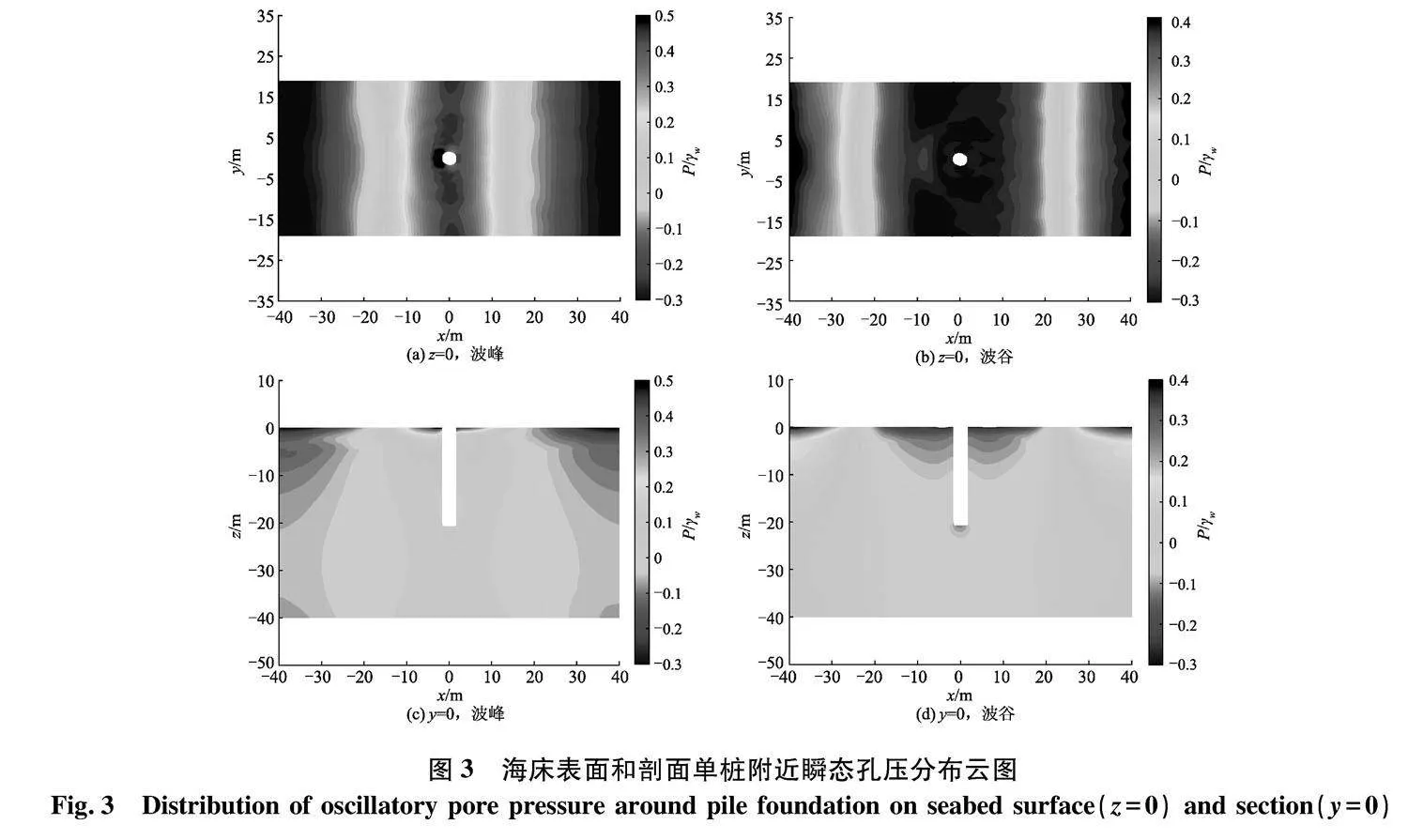
图3为单桩-海床模型瞬态孔压P/γw的俯视和剖面云图，（a）、（c）和（b）、（d）分别为波峰、波谷到达单桩时的瞬态孔压.由图3（a）可知，波峰到达单桩附近时，且桩前土体的瞬态孔压幅值增加.这是由于桩体对波浪的扰动效应，桩前（迎波侧）的波面抬高增加，从而使该处波动压力增大；由图3（b）可知，波谷到达单桩时，波浪发生较为明显的反射和绕射.由图3（c）、（d）可以发现，海床表层土范围内的孔压梯度较大，且具有明显的相位滞后现象，这是海床土体并非完全饱和导致的.

图4为桩周土体累积孔压分布在1个和20个波浪周期下的俯视（z=-1 m表示距海床表面1 m）和剖面云图.如图所示，在波浪的循环荷载下，单桩周围海床0～2 m的浅层土体累积孔压持续增加，且向四周发展.在桩前与桩后位置处，孔压累积最为显著，而在桩侧土体孔压累积的程度相对较小；海床其他区域的累积孔压在20个周期内发展缓慢.

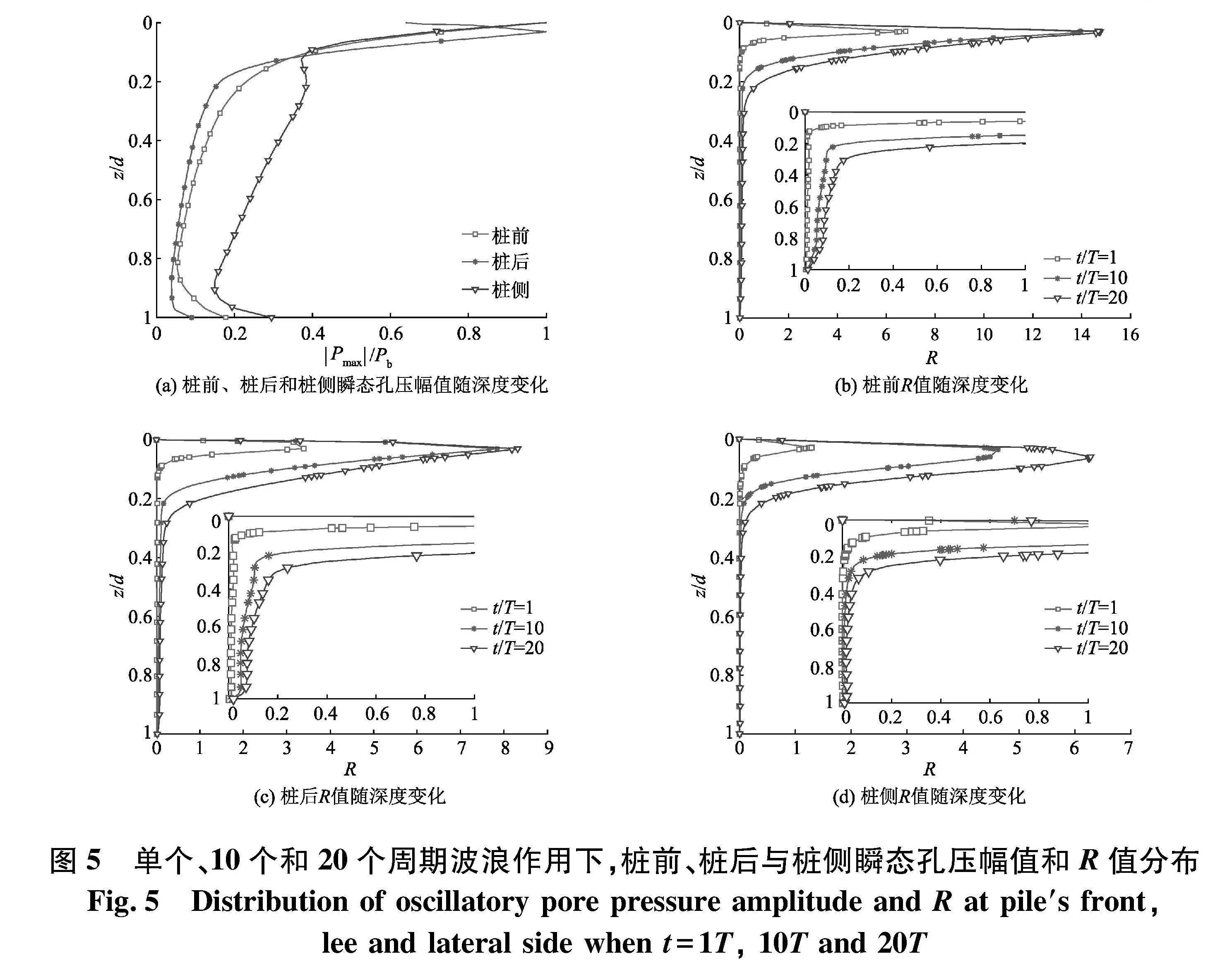
定义一点处累积孔压与该点瞬态孔压幅值的比值为R=Pr/Pmax.当Rlt; 认定瞬态孔压占主导；R=1时，认定瞬态孔压和累积孔压的影响程度相当；当Rgt; 认定累积孔压为主导.图5分别为桩前、桩后、桩侧瞬态孔压幅值（Pb为海床表面处的波浪动压力）和R值的分布.由（a）可知，桩前和桩侧的瞬态孔压幅值沿深度方向减小，而桩后的瞬态孔压幅值在浅层海床表现为先增大后减小；同时，在桩周距土表0～4 m，3处位置的瞬态孔压幅值变化迅速，且在桩末端附近小幅回升，但不超过土表波动压力的30%.另由图5（b）、（c）、（d）可知，20个波浪周期后，桩前孔压累积程度最大，R幅值达14.8；桩后次之，幅值为8.5；桩侧最小，幅值为6.4.这表明随着波浪荷载循环次数的增加，浅层土体中的累积孔压将占主导，且远大于瞬态孔压；剩余范围内，瞬态孔压占主导.在桩末端，R值将小于0.00 说明此处孔压几乎不发生增长.随着波浪荷载持续作用，累积孔压增长速度放缓，Rgt;1的范围不断向下发展.

3.2" 桩周孔压分布受土体参数的影响

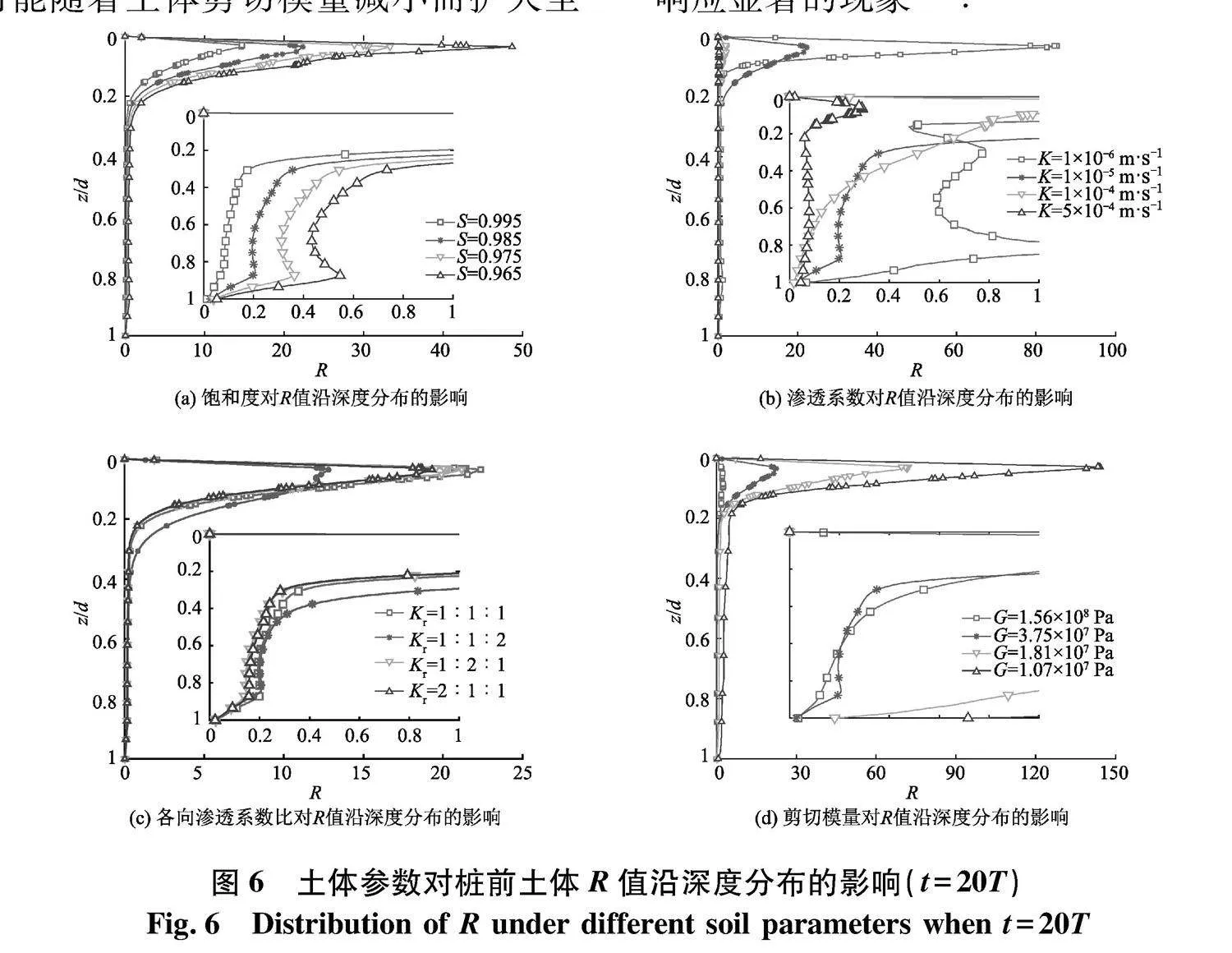
由于三处位置两类孔压分布特征相似，考虑到桩前迎波侧波浪-单桩相互作用明显，选取桩前土体进一步讨论各参数对R值的影响.图6为20个波浪周期后，在不同饱和度S、渗透系数K和各向渗透系数比Kr（=Kx∶Ky∶Kz）下，R值沿海床深度方向的分布.由图 6（a）可以发现，土体饱和度越小，R值越大，表明土体孔压累积程度越大。当饱和度为0.965时，浅层土体中累积孔压值可达到相应位置瞬态孔压幅值的48倍.在桩周距土表4～20 m的海床土体范围内，R值随深度增加逐渐减小至0.01左右，表明瞬态孔压占主导。当饱和度增大，桩周海床R值增加，其中浅层土体的R值受饱和度影响度影响更加明显.

由图 6（b）可知，与饱和度类似，土体R值随着渗透系数减小而增大，且海床浅层土体内R值受渗透系数影响更加显著.当K=5×10-4 m·s时，土体R值将整体小于0. 表明瞬态孔压影响占主导；当K=1×10-6" m·s时，浅层土体中R值最大可至85.3.这一方面是由于浅层土体的波致剪应力随着渗透系数降低而增大，使得累积孔压源项增大；另一方面，土层间的排水性能越差，累积孔压消散得越慢.同时可以发现，土体渗透系数减小，浅层土体的R值梯度增大.这是由于渗透系数越小，不同深度土体的累积孔压发展速率差异越大.

由图 6（c）可知，增加水平向渗透系数有助于降低R值，但对Rgt;1的范围大小几乎无影响；相比之下，竖向渗透系数增加1倍，R值幅值下降48.3%，且累积孔压占主导的区域向下发展.这一趋势表明水平向渗透系数对累积孔压消散影响微弱，而增加土体竖向渗透性能够显著减弱累积孔压发展程度.这是由于沿深度方向累积孔压消散最快，而由于波浪的周期特性，水平向的孔压梯度值存在振荡，不利于孔压消散.

由图 6（d）可知，土体剪切模量越小，R值越大，最大可至144.当剪切模量从3.75×107 Pa降低至1.07×107 Pa，浅层土体R值增大了5.45倍，且桩周土体Rlt;1的区域逐渐消失，表明累积孔压占主导的区域可能随着土体剪切模量减小而扩大至桩体末端.这一结果对应了淤泥质海床中累积孔压响应显著的现象［18］.

3.3" 海床液化深度受土体参数的影响

当土体单元有效应力小于0时，液化即发生.与两种孔压对应，海床液化存在分别以瞬态和累积孔压的液化判别式［3、9］.波浪作用初期，累积孔压未充分发展，土体主要受到垂直向的渗透力-P+Pb，因此初期瞬态液化占主导；随着波浪作用持续，孔压累积的部分逐渐显著，此时应同时考虑两种孔压分量.据此，选择文献［19］改进后的液化判别准则（式（11）），判定波谷到达单桩时桩周土体的最大瞬态液化深度（Pr=0）和最大综合液化深度（Pr≠0）：

σ′0-P+Pb+Pr≤0（11）

3.3.1" 瞬态液化深度

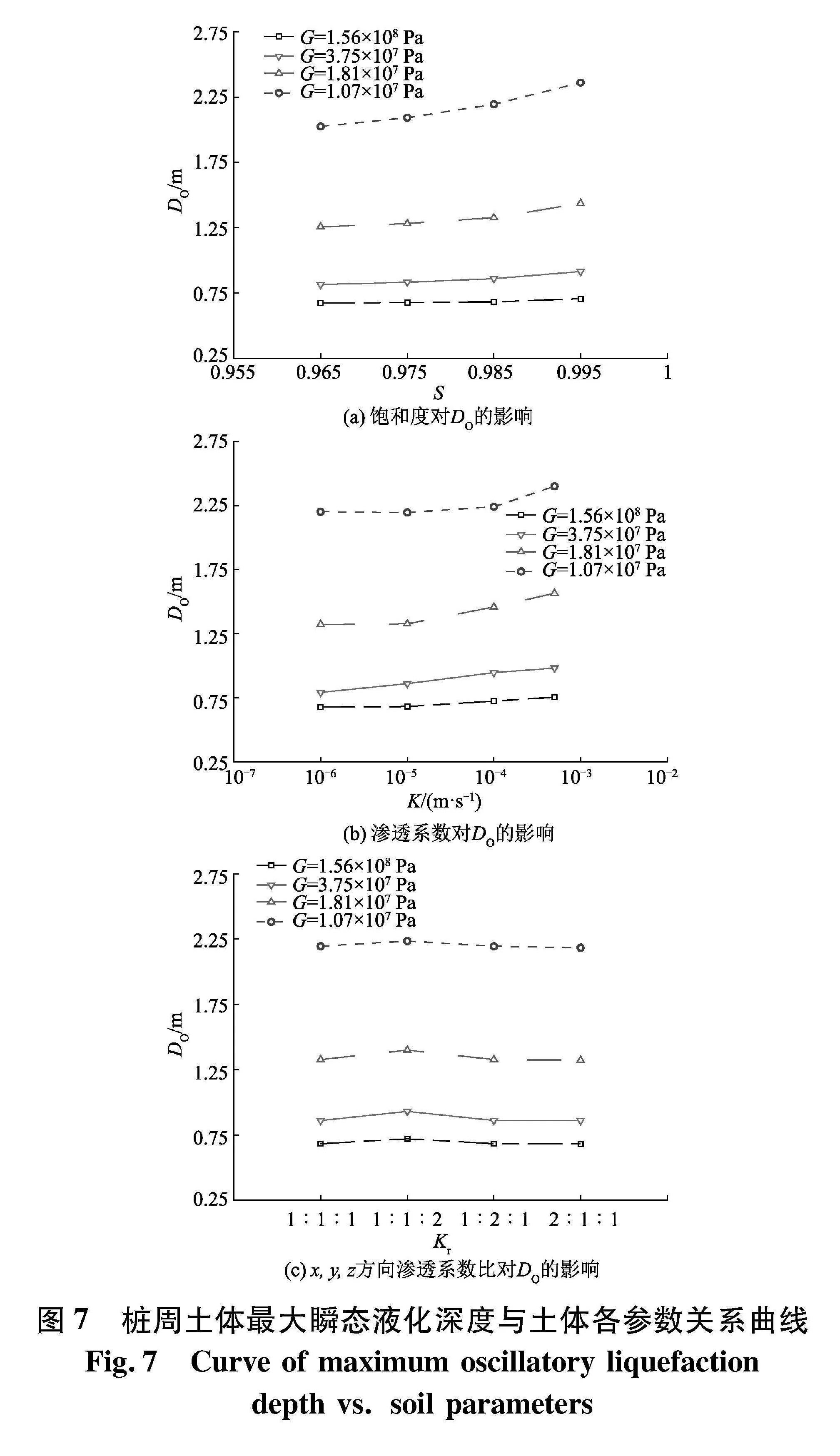
图7给出了波谷到达单桩位置时，桩周土体最大瞬态液化深度Do与土体参数之间的关系曲线.由图 7（a）、（b）、（c）可知，土体剪切模量越小，最大瞬态液化深度越大.当G=1.56×108 Pa时，Do均值为0.7 m.当G=1.07×107 Pa时，Do随G减小而显著增加，均值可达2.2 m.

由图 7（a）、（b）可知，当土体饱和度S和渗透系数K增大，桩周土体最大瞬态液化深度会有一定程度的增长，且在较小剪切模量的土体中，该趋势愈加明显，但幅度最大不超过20%.这可能是由于当土体剪切模量较小时，土体受波浪作用变形较大；而较大的饱和度和渗透系数有助于波浪压力在土体孔隙水中的传递，使得土体超静孔压的影响范围进一步增大.

由图 7（c）可知，增大竖向渗透系数1倍，最大瞬态液化深度有较为明显的增加，而相对增大水平向渗透系数对于最大瞬态液化深度几乎无影响.这是由于水平向渗透系数只影响水平方向的孔压和位移.

3.3.2" 综合液化深度

图8给出了不同土体参数下，桩周土体最大综合液化深度Dr随时间的变化曲线.可以发现，考虑两种孔压响应后的最大综合液化深度表现出振荡和发展特性，且增长速度逐渐放缓.由图8（a）可知，土体饱和度对Dr的发展影响细微.结合图6（a）可推测，这可能是由于饱和度对累积孔压占主导的范围大小影响较小.

由图8（b）可知，K处于1×10-4 m/s至5×10-3 m/s区间时，Dr不再出现累积特性，而振荡特性随渗透系数增大而减弱.对于K=1×10-6 m/s和1×10-5 m/s的结果发现，在20个波浪作用周期后，K=1×10-6 m/s对应的Dr仍处于增长阶段；K=1×10-5 m/s时，Dr已在17个波浪作用周期后稳定.结合图6（b）可推测，这是由于渗透系数的大小影响孔压累积的速率，进而影响液化深度的发展速率。此外，图8（b）暗示了土体的渗透系数存在某一限值，使得在一定波浪条件下，当渗透系数大于该值时，累积孔压分量的影响可以忽略.

由图8（c）可知，相对增大土体水平向渗透系数，能够一定程度上降低最大综合液化深度的发展趋势.这是由于在累积孔压模型方程中，考虑了土体水平向固结系数，当某一方向的渗透系数增大时，有利于累积孔压在该方向上的消散.

由图8（d）可知，当G=1.07×107 Pa时，Dr在20个波浪周期后增长至4.4 m，且振荡范围近0.9 m，分别为G=1.56×108 Pa时对应值的6.3倍和9倍，可见土体剪切模量越小，最大综合液化深度的累积和振荡特性越明显.此外，剪切模量越大，最大综合液化深度的累积部分将越早达到幅值.

4" 结论

对单桩周围海床土体在波浪作用下产生的两类孔压分布特征进行了分析和影响因素研究，并对相应的液化发展特征作了进一步讨论，得到如下结论：

（1） 在桩周距离土表0～4 m（0.2倍单桩嵌入深度）内，桩周土体的瞬态孔压幅值梯度较大，且累积孔压发展迅速，20个波浪周期后其幅值可达到瞬态孔压幅值的144倍.累积孔压占主导的区域随波浪作用时间增加不断下探，但由于深层土体中的动剪应力微弱，其发展速度显著放缓.瞬态孔压幅值随深度增加最终衰减至海床表面动压力的30%以下，占主导的区域处于桩周距土表4～20 m.

（2） 随着土体饱和度、渗透系数和剪切模量减小，累积孔压相对瞬态孔压幅值的比值R增大，瞬态孔压占主导的区域缩小.其中，当渗透系数为10-6量级，浅层土体中R幅值可达85. 同时不同深度土体的累积孔压发展速率差异显著.在剪切模量小于1.07×107 Pa的淤泥质海床中，累积孔压占主导区域可能将发展至20 m.

（3） 当土体剪切模量自1.56×108 Pa缩小至1.07×107 Pa，最大瞬态液化深度均值从0.7 m增大至2.2 m；20个波浪周期后最大综合液化深度从0.7 m增大至4.4 m，同时表现出近0.9 m范围的振荡特性.当渗透系数增大，最大瞬态液化深度有一定的增长，幅度不超过20%；综合液化深度将出现增加的现象。当渗透系数大于1×10-4 m/s，综合液化深度不再发展，但仍表现出明显的振荡性.在剪切模量为1.07×107 Pa的淤泥质海床中，土体饱和度增长3%，最大瞬态液化深度增长13.8%，而最大综合液化深度无明显变化.水平向渗透系数对两类液化深度的影响微弱.

参考文献（References）

［1］" YAMAMOTO T， KONING H L， SELLMEIJER H， et al. On the response of a poro-elastic bed to water waves［J］. Journal of Fluid Mechanics， 1978， 87（1）：193-206.

［2］" MADSEN O S. Wave-induced pore pressure and effective stresses in a porous bed［J］. Geotechnique， 1978， 28（4）：377-393.

［3］" JENG D S. Soil response in cross-anisotropic seabed due to standing waves［J］. Journal of Geotechnical and Geoenvironmental Engineering， 1997， 123（1）：9-19.

［4］" HSU J R C， JENG D S， Wave-induced soil response in an unsaturated anisotropic seabed of finite thickness［J］. International Journal for Numerical and Analytical Methods in Geomechanics， 1994， 18（11）：785-807.

［5］" 隋倜倜， 张弛， 高玉峰， 等. 波浪作用下单桩基础周围海床液化机制研究［J］. 海洋工程， 2018， 36（4）：88-96.

［6］" 于秀霞， 李欣， 凌贤长， 等. 非线性波浪荷载作用下海上风机管桩基础周围海床液化研究［J］. 工程地质学报， 2021， 29（5）：1599-1610.

［7］" ZHAI H， JENG D S. Two-way coupling model for wave-induced oscillatory soil response around marine structures［J］. Ocean Engineering， 2022， 249：110791.

［8］" SEED H B， RAHMAN M S. Wave-induced pore pressure in relation to ocean floor stability of cohesionless soils［J］. Marine Georesources amp; Geotechnology， 1978， 3（2）：123-150.

［9］" MUTLU SUMER B， OZGUR KIRCA V S， FREDSE J. Experimental validation of a mathematical model for seabed liquefaction under waves［J］. International Journal of Offshore and Polar Engineering， 2012， 22（2）：133-141.

［10］" ZHAO H Y， JENG D S， LIAO C C， et al. Three-dimensional modeling of wave-induced residual seabed response around a mono-pile foundation［J］. Coastal Engineering， 2017， 128：1-21.

［11］" SUI T， ZHANG C， JENG D， et al. Wave-induced seabed residual response and liquefaction around a mono-pile foundation with various embedded depth［J］. Ocean Engineering， 2019， 173：157-173.

［12］" 吴仁豪， 嵇春艳， 程勇， 等. 一种浮式防波堤与风机一体化装置设计与性能分析［J］.江苏科技大学学报（自然科学版）， 2022， 36（5）：1-7.

［13］nbsp; JENG D S. Mechanics of wave-seabed-structure interactions： Modelling， processes and applications［M］. UK：Cambridge University Press， 2018：168-168.

［14］" LIU B， JENG D S， YE G L， et al. Laboratory study for pore pressures in sandy deposit under wave loading［J］. Ocean Engineering， 2015， 106：207-219.

［15］" 徐佳丽， 时健， 张弛， 等.近40年中国近海波浪数据库的建立及极值分析［J］.海洋工程，2019，37（6）：94-103.

［16］" 刘博， 刘晋超， 马兆荣， 等.波浪荷载下砂质海床液化抑制的试验研究［J］. 南方能源建设， 2017， 4（4）：100-10 112.

［17］" 吴雷晔， 万佳怡， 孔德琼， 等.波浪作用下软黏土海床动力响应离心模型试验［J］.中南大学学报（自然科学版）， 2022， 53（8）：3040-3051.

［18］" SUI T， ZHANG C， ZHENG J， et al. Numerical study of standing wave-induced seabed residual response with the non-homogeneous soil property［J］. Journal of Coastal Research， 2018 ，85：921-925.

［19］" 栾茂田， 张晨明， 王栋， 等. 波浪作用下海床孔隙水压力发展过程与液化的数值分析［J］. 水利学报， 2004（2）：94-100.

（责任编辑：贡洪殿）