局部视角下的邻域粒度及其属性约简

摘" 要： 在基于粗糙集的粒计算中，邻域粒度是常见的信息粒化表现之一.邻域粒度在不同条件属性之间存在一定差异，如果条件属性生成的邻域粒度越细，那么该条件属性对样本的区分性越强.条件属性在全局样本上生成的邻域粒度，即在全局视角下，会存在一些局限性，例如多个条件属性可能会生成相同或相似的邻域粒度，这样不利于对条件属性作进一步区分.为了弥补这样的缺陷，首先从局部视角出发，提出了局部邻域粒度的概念.与全局视角生成的邻域粒度不同，计算局部邻域粒度首先对全部样本进行分割，然后对分割后的样本分别计算邻域粒度.其次，基于局部邻域粒度提出了一种属性约简改进算法，该算法主要思想是以局部邻域粒度为准则，在选择条件属性时剔除对样本区分性较弱的条件属性.在UCI数据集上选取12组数据集，在两种不同的度量条件下，提出的算法与另外两种算法进行对比实验.实验结果表明，与另外两种算法相比，文中算法在分类准确率和分类稳定性上都有明显优势.

关键词： 属性约简；邻域粒度；邻域粗糙集；局部邻域粒度

中图分类号：TP18"" "文献标志码：A""""" 文章编号：1673-4807（2024）05-092-08

DOI：10.20061/j.issn.1673-4807.2024.05.014

收稿日期： 2023-08-26""" 修回日期： 2021-04-29

基金项目： 国家自然科学基金项目（62006099， 62076111）；浙江省海洋大数据挖掘与应用重点实验室开放课题（OBDMA202104）

作者简介： 徐天喜（1999—）， 男，硕士研究生

*通信作者： 宋晶晶（1990—），女，博士， 副教授， 研究方向为模糊集、粗糙集、粒计算. E-mail： songjingjing108@163.com

引文格式： 徐天喜，宋晶晶，陈建军，等.局部视角下的邻域粒度及其属性约简［J］.江苏科技大学学报（自然科学版），202 38（5）：92-99.DOI：10.20061/j.issn.1673-4807.2024.05.014.

Neighborhood granularity and attribute reduction from a local perspective

XU Tianxi1，SONG Jingjing1*，CHEN Jianjun1，XU Taihua1， 2

（1.School of Computer， Jiangsu University of Science and Technology， Zhenjiang 212003， China）

（2.Key Laboratory of Marine Big Data Mining amp; Application， Zhejiang Ocean University， Zhoushan 316022， China）

Abstract：In granular computing based on rough sets， neighborhood granularity based on neighborhood relationships is one representation of information granulation. The neighborhood granularity generated by different conditional attributes， and finer neighborhood granularity can result in a stronger differentiation of samples by the conditional attributes. However， previous research has mostly focused on the global perspective of neighborhood granularity generated by conditional attributes on the whole sample set， which may have limitations. For example， multiple conditional attributes may generate similar neighborhood granularities， making it difficult to differentiate the conditional attributes further. To fill the gap， this paper proposes the concept of local neighborhood granularity from a local perspective. Different from global neighborhood granularity， firstly the whole sample set is partitioned when calculating local neighborhood granularity and then the neighborhood granularity computed for each partition. Based on local neighborhood granularity， this paper proposes an attribute reduction algorithm that uses local neighborhood granularity as a criterion and remove conditional attributes having weak discriminative power for the samples when selecting conditional attributes. The proposed algorithm is compared with other algorithms using two different metric criteria in experiments performed on 12 UCI datasets. The experimental results show that the proposed algorithm has significant advantages in classifying accuracy and stability compared with the other algorithms.

Key words：attribution reduction， neighborhood granularity， neighborhood rough set， local neighborhood granularity

粗糙集理论［1］是一种处理不确定信息的数学工具，在数据挖掘、人工智能等领域受到学者们的广泛关注.但是，最初的粗糙集理论不适用于处理连续型数据，因此，对粗糙集模型进行了扩展.文献［2］结合粗糙集理论和模糊集理论提出模糊粗糙集理论，模糊粗糙集理论将粗糙集理论中的等价关系替换为模糊相似关系.文献［3］针对粗糙集模型的基本假设为单尺度问题提出了Wu-Leung模型，使得粗糙集理论可在不同尺度下对数据进行表示、分析和决策.

为了进一步拓展粗糙集的应用范围，文献［4］基于邻域关系，提出了邻域粗糙集.从粒计算的角度来看，邻域可以有效并且直观地解释信息粒和信息粒化的过程从而得到许多学者的青睐.随着对邻域粗糙集的深入研究，发现邻域粗糙集可能面临着两种挑战：挑战一在于邻域半径对整个邻域粗糙集模型影响较大.文献［5］发现在数据的原始标签下，邻域半径对邻域关系的分辨能力的影响过于苛刻，于是结合无监督和半监督学习任务中的伪标签策略提出了基于伪标签邻域关系的伪标签邻域粗糙集.为了解决无监督下的邻域关系可能导致邻域信息不一致或不精确的问题，文献［6］提出了有监督下邻域信息粒化策略，通过类内半径和类外半径从邻域中删除不同标签样本.文献［7］提出粒球粗糙集模型，实现了自适应信息粒化.挑战二在于邻域粗糙集在处理大规模数据集时计算复杂度较高.文献［8］基于局部粗糙集提出局部邻域粗糙集模型，该模型在处理大规模数据集时，具有显著的算法效率优势.文献［9］采用邻域粒度压缩了候选条件属性的空间，虽然一定程度上提高了约简算法的执行效率，但是仍然避免不了对条件属性的迭代计算.文献［10］采用邻域粒度从细粒度到粗粒度的方式对条件属性进行预排序，省去了对条件属性的迭代计算，提高了算法的执行效率.

文中从局部的视角提出局部邻域粒度的概念，基于局部邻域粒度，同时结合排序思想设计一种新的属性约简算法.不同于全局邻域粒度的计算方法，在计算局部邻域粒度时，需要将一个样本集分割为多份，得到多个样本子集.根据样本的决策属性将样本集进行分割，然后在每个样本子集上计算邻域粒度.与全局邻域粒度相比，局部邻域粒度可以更详细地体现条件属性间的差别，有利于提高约简算法的分类准确率和分类稳定性.

1" 背景知识

1.1" 邻域粗糙集

在邻域粗糙集中，可以用一个二元组DS=lt;U，AT∪{d}gt;表示一个决策系统，U={x1，x2，…，xn}是所有样本的非空有限集合，被称为论域，AT是条件属性的集合，AAT，由A诱导的不可分辨关系表示为INDA={x，y∈U2：a∈A，ax=a（y）}，d是决策属性.根据决策属性将论域划分为n个等价类，表示为U/INDd={X1，X2，…，Xn}.

定义1［4］" 给定一个决策系统DS=lt;U，AT∪{d}gt;，AAT，x，y∈U，样本x，y之间欧式距离SA（x，y）为：

SA（x，y）=" ∑a∈A（a（x）-a（y））2（1）

定义2［4］" 给定一个决策系统DS=lt;U，AT∪{d}gt;，AAT，σ是给定的邻域半径，由条件属性子集A生成的邻域关系 RA为：

RA={（x，y）∈U2|SA（x，y）≤σ}（2）

xi∈U，根据邻域关系RA可以得到xi的邻域RA（xi），RAxi={xj∈U：（xi，xj）∈RA}.

定义3［4］" 给定一个决策系统DS=lt;U，AT∪{d}gt;，AAT，等价类Xn关于条件属性子集A的上下近似集合定义为：

NA（Xn）={x∈U：RA（x）∩Xn≠}

NA（Xn）={x∈U：RA（x）Xn}（3）

1.2" 相对邻域自信息

在邻域粗糙集中，上近似集合中样本的信息往往会被忽略.文献［11］不仅考虑了下近似集合中样本的信息，而且利用了易被忽略的上近似集合中样本的信息，提出了相对邻域自信息，使构造出的度量函数更加全面.

定义4［11］" 给定一个决策系统DS=lt;U，AT∪{d}gt;，d是决策属性，AAT，等价类Xn关于条件属性子集A的决策精度μA（Xn）和粗糙度VA（Xn）分别为：

μA（Xn）=NA（Xn）NA（Xn）

VA（Xn）=1-μA（Xn）（4）

式中：NA（Xn）为下近似集合中的样本数量；NA（Xn）为上近似集合中的样本数量；μA（Xn）和VA（Xn）的取值范围都为［0，1］.

定义5［11］" 给定一个决策系统DS=lt;U，AT∪{d}gt;，Xn∈U/INDd，AAT，相对邻域自信息定义为：

IA（Xn）=-VA（Xn）log μA（Xn）

IA（d）=∑ni=1IA（Xn）（5）

IA（Xn）表示的是等价类Xn关于条件属性子集A的相对邻域自信息，所有等价类的相对邻域自信息的和就构成了整个决策系统的相对邻域自信息IA（d），当IA（d）等于0时，U中的所有样本都可以通过条件属性子集A完全分类到它们各自的类别中.从相对邻域自信息的定义可以看出，相对邻域自信息不仅包含上近似集合中样本的信息还包含下近似集合中样本的信息.同时，如果一个条件属性子集的相对邻域自信息越小，说明该条件属性子集越有助于样本分类.

1.3" 邻域判别指数

定义6［5］" 给定一个决策系统DS=lt;U，AT∪{d}gt;，AAT，条件属性子集A的邻域判别指数定义为：

NDIAd=logRARA∩INDd（6）

式中：RA表示由条件属性子集A生成的邻域中的样本数量，RA∩INDd表示条件属性子集A生成的邻域与决策属性d生成的不可分辨关系INDd的交集中的样本数量.

NDIA（d）代表邻域关系的判别能力，NDIA（d）指数越小，邻域关系的判别能力越强，当NDIA（d）为0时，U中的所有样本都可以通过条件属性子集A完全分类到它们各自的类别中.

1.4" 属性约简

属性约简［6，9］原始条件属性基础之上，删除一些冗余的条件属性，进而对数据进行降维，降低了后续学习的复杂性，提高学习器的泛化能力，所以被广泛应用于机器学习、数据挖掘等领域.文献［12］总结了属性约简的一般形式，如定义7.

定义7［12］" 给定一个决策系统DS=lt;U，AT∪{d}gt;，AAT，Cρ是关于度量ρ的约束条件，包容度ε，若A满足以下条件，则称A是关于Cρ的一个约简.

（1） A满足约束条件Cρ.

（2） A′A，A′不满足约束条件.

根据不同的度量构建约束条件时，一般情况下要考虑度量的正相关性和负相关性.如果度量ρ是正相关的，则度量值越高越好.例如，近似质量［4］，此时Cρ通常表示为ρ（A）ρ（AT）·ε；如果度量ρ是负相关的，则度量值越低越好.例如上面介绍的相对邻域自信息，此时Cρ通常表示为ρ（A）·ε≤ρ（AT），其中ε是包容度，是为了防止约束条件过于严苛，导致约简过程中删除过多属性而设置的.

基于属性约简的一般形式采用不同类型的搜索算法，贪心搜索算法因其较快的迭代速度，较低的时间复杂度而受到学者们的关注［9］.算法1介绍了前向贪心属性约简算法求解过程.

算法1：前向贪心属性约简算法

输入：一个决策系统DS=lt;U，AT∪{d}gt;，度量ρ.

输出：约简集合red.

（1）初始化，令red=；

（2）While red不满足约束条件Cρ do

（3）a∈AT-red，计算ρ（red∪{a}）；

（4）找出当前迭代过程中一个合适的条件属性b∈AT-red；

（5）red=red∪{b}；

（6）计算ρ（red）；

（7）End while

（8）Return red.

在算法1执行过程中，首先将约简集合初始化为空集合，根据度量选择合适的属性，直至整个约简集合满足对应的约束条件，然后返回约简集合，最后算法结束.

算法1在每次迭代的过程中，需要对候选池中所有条件属性进行评估，这种方式显然是费时的.在求解约简的过程中，考虑在最坏的情况下，条件属性集合AT中的每个条件属性都需要被评估，所以算法1的时间复杂度为O（U2·AT2）.

1.5" 全局邻域粒度

在粒计算理论中，粒度这一概念通常反映了信息粒化的程度.目前对粒度的语义解释［9］分为：

（1） 基于参数的粒度.粒度与指定的参数密切相关.一般情况下，较小的参数值会生成更加精细的粒度.例如，在邻域粗糙集中，较小的邻域半径可以生成较小的样本邻域，因此将获得更细的粒度.

（2） 基于属性的粒度.通常来说，如果属性的区分性越强，那么该属性就会生成更精细的粒度.例如，在邻域粗糙集中，相同的邻域半径下，不同条件属性集合所生成的粒度可能是不同的.当条件属性的个数越多，粒度值越小，样本间的区分度就越大.

（3） 基于样本的粒度.不同样本集之间的粒度是有所不同的.例如，在5折交叉验证中，将原始样本均分为5组不同的训练集和测试集，这一过程产生了5种信息粒化的结果，因为每组的样本集所包含的测试集和训练集是明显不同的.

基于邻域关系生成的粒度既体现了基于参数的粒度，又体现了基于属性的粒度［9］.下面将介绍关于全局邻域粒度的相关定义和性质.

定义8［10］" 给定一个决策系统DS=lt;U，AT∪{d}gt;，AAT，全局邻域粒度定义为：

GA（U）=∑xn∈URA（xn）U2（7）

式中：RA（xn） 为xn邻域中的样本数量；U为整个样本集的样本数量；GA（U）的取值范围为［1U，1］.GA（U）反映某一条件属性子集在全局样本上生成的邻域粒度粗细.换句话说，GA（U）的值越小，代表条件属性子集生成的邻域粒度越细，该条件属性子集越有助于对样本进行区分.GA（U）的值越大，代表条件属性子集生成的邻域粒度越粗，该条件属性子集越不利于对样本进行区分.

根据定义 在相同样本下，根据不同条件属性生成的邻域粒度大小对条件属性进行区分.文献［10］基于全局邻域粒度提出了一种对条件属性预排序的算法.该算法先在整个样本集上，求出每个条件属性生成的全局邻域粒度，然后依据这些粒度值对条件属性进行升序排列.在属性约简的过程中，先考虑全局邻域粒度较细的条件属性，并且这一算法避免了算法1中会对条件属性迭代计算的缺点，因此降低了属性约简算法的时间复杂度.算法2将详细介绍该算法流程.

算法2：基于全局邻域粒度的属性约简算法

输入：一个决策系统DS=lt;U，AT∪{d}gt;，度量ρ，邻域半径σ.

输出：约简集合red.

（1） 初始化，令red=；

（2） ak∈AT，计算Gak（U）；

（3） 根据步骤2计算的邻域粒度对条件属性进行升序排序：a a …，ak；

（4） While red不满足约束条件Cρ do

（5） For i=" …，k do

（6） red=red∪{ai}

（7） If red满足约束条件Cρ then

（8） Break;

（9） Else if then

（10） 返回步骤6；

（11） End if

（12） End for

（13） End while

（14） Return red.

在算法2中，条件属性集合AT中的所有条件属性都已经预先进行了排序，在求解约简的过程中，只需要依次将条件属性放入约简集合中.在最坏的情况下，条件属性集合AT中的所有条件属性都需要进行评估，因此算法2的时间复杂度为O（U2·AT）.

2" 局部邻域粒度属性约简

2.1" 局部邻域粒度

从全局的角度出发往往会忽略局部的细节，在利用全局邻域粒度进行属性约简的过程中，可能会存在多个不同的条件属性生成相同或相似的邻域粒度，这样会对属性约简造成一定的困扰.

定义9" 给定一个决策系统DS=lt;U，AT∪{d}gt;，AAT，Xn∈U/INDd，条件属性子集A在某一等价类Xn样本上生成的局部邻域粒度：

LGAXn=∑xn∈XnRAxnXn2（8）

式中：Xn为等价类Xn样本的数量；LGA（Xn）的取值范围为［1Xn，1］.

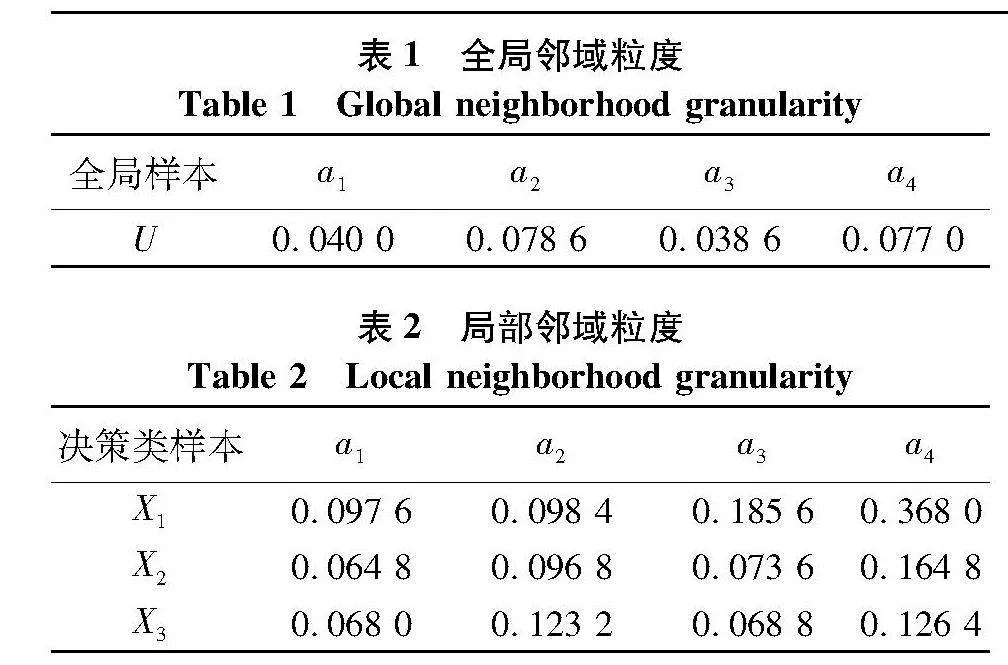
局部邻域粒度LGA（Xn），反映了条件属性子集在不同等价类样本上生成邻域粒度的粗细.LGA（Xn）的值越小，说明该条件属性子集在某个等价类样本上生成的邻域越细，该条件属性子集就越有利于样本间的区分.用例1来说明全局邻域粒度与局部邻域粒度的区别.

例1.以UCI公开数据集中选取的“Iris”数据集为例，Iris数据集拥有150个样本，5个属性，其中包括4个条件属性、1个决策属性.决策属性分为3种，每种样本的个数为50个.在此数据集上取相同的邻域半径（取0.01），观察各条件属性在全局样本上生成的全局邻域粒度与在各个决策类样本上生成的局部邻域粒度之间粒度的区别.

表1是各个条件属性在全局样本下生成的邻域粒度，表2是各个条件属性在不同决策类样本上生成的局部邻域粒度.观察表 条件属性a2和a 两者的邻域粒度分别为0.078" 0.077" 那么在这种情况下，以全局的角度观察两个条件属性对样本的区分程度是相似的.以局部的角度去观察，表2中，条件属性a2和a4在等价类X1上生成的邻域粒度分别为0.098" 0.368" 并且a2生成的粒度明显比a4生成的要细.因此在局部视角下，a2对样本的区分能力更强，所以在属性约简的过程中应该优先选择条件属性a2.

2.2" 局部邻域粒度属性约简算法

为了弥补不同条件属性可能会在全局样本上生成相同或相似的邻域粒度这样的缺陷，提出局部邻域粒度的相关概念，并结合算法2的排序思想，设计了新的属性约简算法，文中简称算法3.在算法3中通过对样本的分割，构造多个样本子集，从而对不同条件属性的邻域粒度进行更加详细的对比.

算法3：基于局部邻域粒度的属性约简算法

输入：一个决策系统DS=lt;U，AT∪{d}gt;，度量ρ，邻域半径σ.

输出：约简集合red.

（1） 初始化，令red=；

（2） For Xi in U/INDd do

（3） ak∈AT，计算LGak（Xi）；

（4） End for

（5） For ak in AT do

（6） ak∈AT，MLGak=min（LGak（Xi））；

（7） End for

（8） 根据步骤6计算的MLGak对条件属性进行升序排序：a a …，ak；

（9） While red不满足约束条件Cρ do

（10） For i=" …，k do

（11） red=red∪{ai}

（12） If red满足约束条件Cρ then

（13） Break;

（14） Else if then

（15） 返回步骤11；

（16）" End if

（17） End for

（18） End while

（19） Return red.

算法3在求解约简的过程中同样预先对条件属性进行了排序，在最坏的情况下，条件属性集合AT中的所有条件属性都需要进行评估，因此算法3的时间复杂度为O（U2·AT）.

例2.用一个简单的例子对算法3的流程进行说明.以表2中在Iris数据集上求得的局部邻域粒度为例，以邻域判别指数为度量，算法3的具体过程如下：

（1） 令约简集合red=.

（2） 根据公式（6）计算NDIAT（d）=0.

（3） 计算各个条件属性在每类样本上的邻域粒度大小.

（4） 选择每个条件属性最小的邻域粒度值为：a1=0.064" a2=0.096" a3=0.068" a4=0.126 4.

（5） 对条件属性进行排序：a a a a4.

（6） 将条件属性a1加入到约简集合red之中，此时red={a1}，计算NDIred（d）=1.736" NDIred（d）·0.95 =1.649" 所以NDIred（d）·0.95gt;NDIAT（d），不满足约束条件，所以继续选择条件属性.

（7） 将条件属性a3加入到约简集合red之中，此时red={a1，a3}，计算NDIred（d）=1.386" NDIred（d）·0.95 =1.317" 所以NDIred（d）·0.95gt;NDIAT（d），不满足约束条件，所以继续选择条件属性.

（8） 将条件属性a2加入到约简集合red之中，此时red={a1，a3，a2}，计算NDIred（d）= NDIred（d）·0.95 = 所以NDIred（d）·0.95=NDIAT（d），满足约束条件，所以停止选择条件属性.

（9） 返回约简集合red={a1，a3，a2}.

3" 实验分析

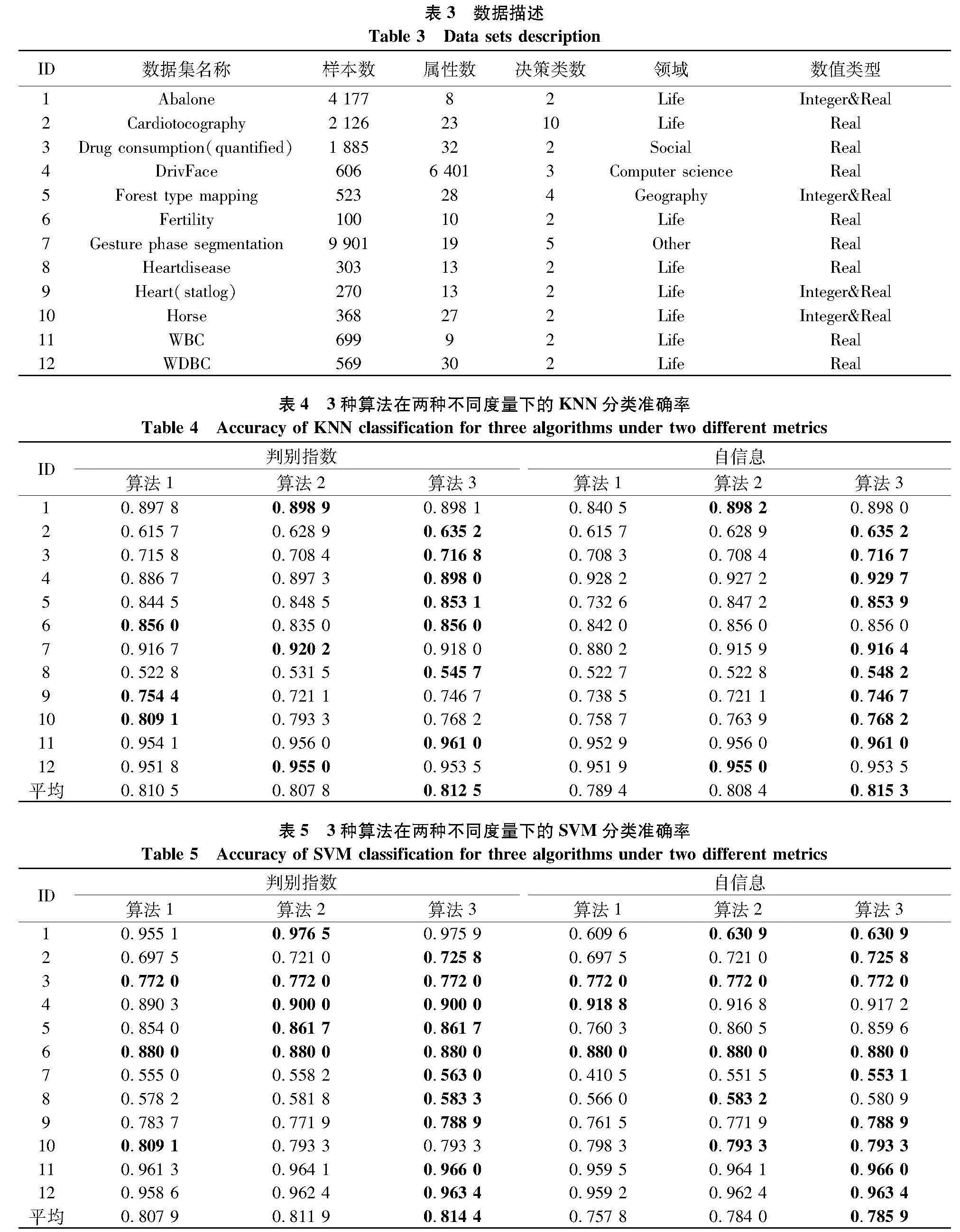
为了验证所提出算法的有效性，从UCI数据集（https：∥archive-beta.ics.uci.edu/）上选取12组数据集进行实验，数据集的具体描述如表 实验均采用MATLAB R2017a实现，操作系统为Windows 1 CPU为Intel Core i7-8750H，内存为16.00 GB.

3.1" 分类准确率对比

实验采用K最近邻（K-nearest neighbor，KNN）（K=3）和支持向量机（support vector machine，SVM）（默认参数）两种分类器分别对所求得的约简的分类性能进行测试.根据以往的经验，为防止过大的邻域半径导致保留过多冗余条件属性，邻域半径取0.02～0. 步长为0.0 共10个半径，包容度ε取0.95.在每个半径下，进行10折交叉验证，每一轮使用9折样本求得约简结果后，使用剩下的样本进行分类测试，最终对每个半径下的平均分类准确率取平均值，其结果分别如表4和表5.

表4和表5分别是3种不同算法在邻域判别指数（表中简称判别指数）和相对邻域自信息（表中简称自信息）为度量下的准确率.在3种算法的对比实验结果中，实验最优的结果已被加粗显示，以便观察实验结果.通过对比表4和表5所描述的结果，可以发现：

（1） 文中提出的算法3在决策属性类别较多的样本集有比较好的表现，以表4中有10种决策属性类别的“Cardiotocography（ID：2）”为例，在表4中3种算法采用两种不同的不确定性度量进行约束，算法1和算法2在邻域判别指数下的所求得约简对应的KNN分类准确率分别为0.615 7和0.628" 算法3对应的KNN分类准确率为0.635 2.

（2） 通过观察表4和表 不论是以邻域判别指数还是以相对邻域自信息构造约束，算法3在KNN分类器和SVM分类器上拥有最好的平均分类准确率.以表5中的SVM平均分类准确率为例，算法1和算法2在邻域判别指数下的所求得的约简对应的平均SVM分类准确率分别为0.807 9和0.811" 算法3对应的平均SVM分类准确率为0.814 4.

上述对实验结果的观察分析是在相同的不确定性度量下对比不同算法之间的分类准确率.换个角度，观察相同算法在不同的不确定性度量的分类准确率差别.

算法2和算法3在SVM分类器下对不同的度量拥有相同的分类准确率，以表5中的数据集“Heart（statlog）（ID：9）”为例，算法3在以邻域判别指数为约束的情况下，KNN的分类准确率为0.788" 在相对邻域自信息为约束的KNN分类准确率同样是0.788 9.这种情况可能有以下两种原因造成的.

首先，可能是邻域判别指数和相对邻域自信息这两种度量之间存在相似性，两种度量都是负相关的，意味着两者都是度量值越低，表明条件属性分类能力越强.

其次，算法2和算法3在约简过程中都是根据条件属性的邻域粒度提前对其进行排序，选择条件属性时不会受度量的影响.但是算法1是根据度量值挑选合适的条件属性，所以在约简过程中会受到不同度量的影响.这也从侧面反映算法2和算法3面对不同的度量时可能会有更好的稳定性.

3.2" 分类稳定性对比

分类稳定性［13］是一种对约简后条件属性的分类稳定性的衡量方法，例如执行两次约简算法，两次约简结果在分类器上预测结果完全一致，则该约简算法的分类稳定性就是1.分类稳定性越高，则代表后续学习结果越稳定.

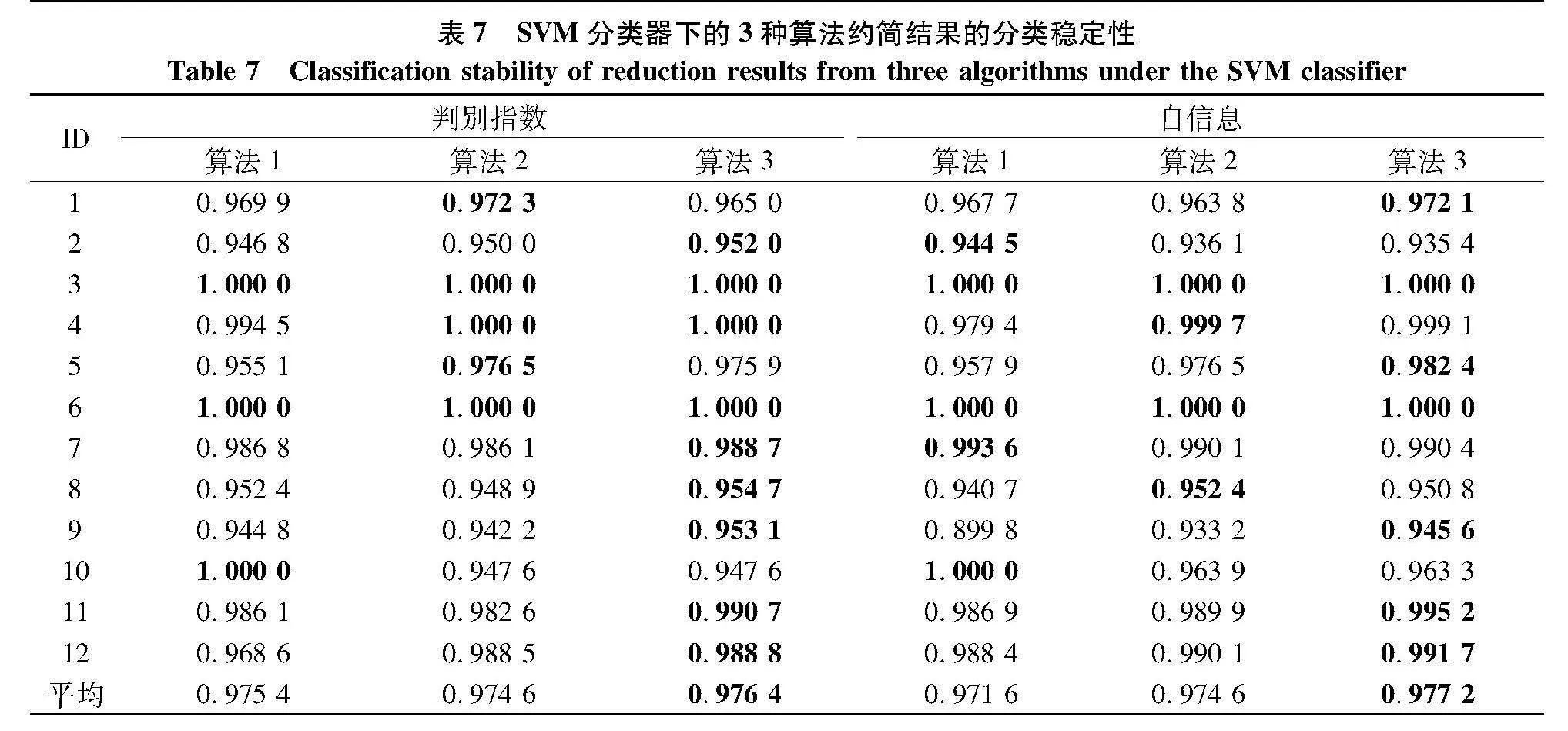
为确保实验的有效性，同样使用10折交叉验证法进行实验.表6和表7分别描述的是各算法在两种不同的度量下求出的约简结果，在KNN分类器和SVM分类器的分类稳定性对比.通过对比表6和表7所描述的结果，可以发现：

（1） 当条件属性较多时，文中提出的算法3拥有较高的分类稳定性.以表6中有6 401个属性的“DrivFace（ID：4）”为例，算法1和算法2在邻域判别指数下的所求得的约简对应的KNN分类稳定性分别为0.989 0和0.995" 算法3对应的KNN分类稳定性为0.996 0.算法1和算法2在相对邻域自信息下所求得的约简对应的KNN分类稳定性分别为0.979 5和0.988" 算法3所对应的KNN分类稳定性为0.991 0.

（2） 相比算法 算法2和算法3在大多数据集上拥有更高的分类稳定性，在表7中，以数据集“Heart（statlog）（ID：9）”为例，算法2和算法3在相对邻域自信息下所求得的约简对应的SVM分类稳定性分别为0.933 2和0.945" 算法1对应的SVM分类稳定性为0.899 8.就平均稳定性而言，算法3与其他算法相比也具有优势，算法1和算法2在邻域判别指数下的所求得的约简对应的平均SVM分类稳定性分别为0.975 4和0.974" 算法3的对应的平均稳定性为0.976 4.

相较于算法1和算法2而言，文中提出的基于局部邻域粒度的算法3在大多数的数据集上，不论是以邻域判别指数还是相对邻域自信息为度量，都有着较高的分类准确率和分类稳定性.

4" 结论

文中从局部的视角出发，观察不同条件属性在局部样本上的邻域粒度的差别，发现不同条件属性在全局生成的邻域粒度相同或相似的时候，其在局部样本上生成的邻域粒度差异较大.这就意味着相较于全局邻域粒度而言，局部邻域粒度可以更好的进行属性约简.实验表明，提出的算法3在提高分类器的准确率和分类稳定性上都有着不错的效果.

文中仅使用了两种不确定性度量进行求解，下一步可以尝试其他不确定性度量来验证算法的有效性，例如近似质量等.算法3是根据邻域粒度观察不同条件属性的差异，下一步可以考虑在相同条件属性下通过粒度考虑样本之间的差别.

参考文献（References）

［1］" PAWLAK Z. Roughsets［J］.International Journal of Intelligent Systems，1982，11（5）：341-356.

［2］" DUBOIS D， PRADE H. Rough fuzzy sets and fuzzy rough sets［J］. International Journal of General Systems， 1990， 17（2）：191-209.

［3］" WU W， LEUNG Y. Theory and applications of granular labeled partitions in multi-scale decision tables［J］. Information Sciences， 2011， 181（18）：3878-3897.

［4］" HU Qinghua， YU Daren， LIU Jinfu， et al. Neighborhood rough set based heterogeneous feature subset selection［J］. Information Sciences， 2008， 178（18）：3577-359.

［5］" YANG Xibei， LIANG Shaochen， YU Hualong， et al. Pseudo-label neighborhood rough set： Measures and attributereductions［J］. International Journal of Approximate Reasoning， 2019， 105：112-129.

［6］" LIU Keyu， YANG Xibei， YU Hualong， et al. Supervised information granulation strategy for attribute redction［J］. International Journal of Machine Learning and Cybernetics，2020，11：2149-2163.

［7］" XIA Shuyin， ZHANG Hao， LI Wenhua， et al. GBRS： A novel rough set algorithm for fast adaptive attribute reduction in classification［J］.IEEE Transactions on Knowledge and Data Engineering，2022，34（3）：1231-1242.

［8］" WANG Qi， QIAN Yuhua， LIANG Xinyan， et al. Local neighborhood roughset［J］.Knowledge-Based Systems， 2018， 153：53-64.

［9］" 张昭琴，徐泰华，鞠恒荣，等.基于粒度的加速求解约简策略［J］.南京理工大学学报（自然科学版），2021，45（4）：401-408.

［10］" BA Jing， WANG Pingxin， YANG Xibei， et al. Glee： A granularityfilter for feature selection［J］. Engineering Applications of" Artificial Intelligence， 2023， 122：106080.

［11］" WANG Changzhong， HUANG Yang， SHAO Mingwen， et al. Feature selection based on neighborhood self-information［J］. IEEE Transactions on Cybernetics， 2020， 50（9）：4031-4042.

［12］" YAO Yiyu， ZHAO Yan， WANG Jue. On reduct construction algorithms［C］∥Transactions on Computational Science II. Berlin： Springer， 2008： 100-117.

［13］" YANG Xibei， YAO Yiyu. Ensemble selector for attribute reduction［J］.Applied Soft" Computing，2018，70：1-11.

（责任编辑：曹莉）