基于风险预警-遗传算法耦合的河道水利工程设施巡查路线规划研究
2024-11-10罗港林远勤周新民林旭


摘 要:传统的河道水利工程设施巡查选点及路线规划高度依赖工作人员从业经验,容易造成巡查选点覆盖面不足,不能及时发现河道水利工程设施问题,因此如何开展河道巡查路线规划,合理规划巡河路线,实现对存在风险隐患的水利工程设施巡查更广泛的覆盖面以及更高效的巡查效率很有必要。基于风险预警-遗传算法耦合的方法,研究建立河道水利工程设施风险预警模型与河道巡查路线规划模型,实现了对河道水利工程设施巡查路线规划。中河道水利工程设施风险预警模型采用熵权-Topsis方法计算得出巡查对象风险等级,通过耦合基于遗传算法的河道巡查路线规划模型,以巡查对象风险等级作为河道巡查路线规划模型输入数据,最终求解出河道巡查路线。通过在广州市河涌监测中心日常巡河作业实践应用证明,基于风险评估-遗传算法耦合方法规划的巡河路线较传统经验路线更合理,在风险设施巡查覆盖面及巡查时间效率上都有更佳的表现。
关键词:风险预警;路线规划;河道巡查;水利工程设施
中图分类号:TV1 文献标识码:A 文章编号:1001-9235(2024)09-0110-08
1 研究背景
近年来,广东各地在加大河长制、湖长制激励问责方面创新方式方法,有效促进各级河长湖长和责任部门履职尽责,为了提高河道巡查效率,广州市河涌监测中心通过建立基于河道巡查工作的河道及附属设施风险预警模型、河道巡查路线规划模型,持续推进差异化巡河机制的技术应用和治理探索。
河道水利工程设施巡查是保障水利工程安全运行的重要工作,是河道管理的重要组成部分,如何对现场巡查现状快速做出决策,促进决策人员对河道水利工程设施巡查规划功能加强的需求日益增加。因此,更加先进的规划策略引进将会给巡查工作带来更大的优势。
目前传统的河道水利工程设施巡查选点及路线规划高度依赖工作人员从业经验,容易造成巡查选点覆盖面不足,不能及时发现河道水利工程设施问题。为此,有必要开展河道巡查路线规划研究,合理规划巡河路线,实现对存在风险隐患的水利工程设施巡查更广泛的覆盖面以及更高效的巡查效率。
河道水利工程设施巡查路线规划问题类似于旅行商(Travelling Salesman Problem, TSP)[1-2]问题,是组合优化领域的典型问题,TSP一直以来都是计算机科学中的热门研究课题,描述为1个商人从任意城市出发,不重复不遗漏地访问每一个城市,最后返回出发地,其目标是找出一条包含所有城市的最短路径。
目前求解旅行商问题的算法有多种,主要可分为两类,分别为精确算法和启发式算法。精确算法能够得出旅行商问题的最优解,但是随着要求的问题规模变大,精确算法的时间复杂度也迅速增加,因此,使用启发式算法求解旅行商问题是目前的1个热点研究方向。关于求解TSP方面,学者们已开展了大量的研究,比如2020年,Cinar等[3]重新设计基本TSA,解决了置换编码的优化问题,提出了DTSA来解决TSP。2022年,Zhang等[4]提出了DSSA算法,该算法设计了一种全局扰动策略,DSSA算法在求解TSP 中具有较强的竞争性和鲁棒性。2022年,Skinderowicz[5]提出了FACO算法,该算法在求解大规模实例时,性能优于目前的许多ACO算法。
目前,解决TSP已经存在了许多成熟的算法,这些算法能够在较短的时间内求得TSP较优的近似解或者最优解。然而,随着TSP数据规模的增大,这些算法的效率和性能也会遇到一些瓶颈,例如求解时间变长或者陷入局部最优解。因此,在这些算法的基础上,科学家们也着重于研究进一步提高算法的求解速度和求解质量,以此来满足日益增长的数据规模。
2 技术路线
河道水利工程设施巡查路线规划[6-9]问题类似于旅行商问题[10-11],是组合优化领域的典型问题。TSP可描述为1个商人从任意城市出发,不重复不遗漏地访问每一个城市,最后返回出发地,其目标是找出一条包含所有城市的最短路径。
河道水利工程设施巡查路线规划问题有别于一般TSP,一般TSP的假设前提是每个需要经过的“城市”重要性权重都是一样的。河道水利工程设施巡查路线规划问题则需要考虑水利工程设施风险等级,风险等级越高,需要巡查的概率应越高。以此,在求解TSP前,首先需要正确评估水利工程设施风险等级[12]。
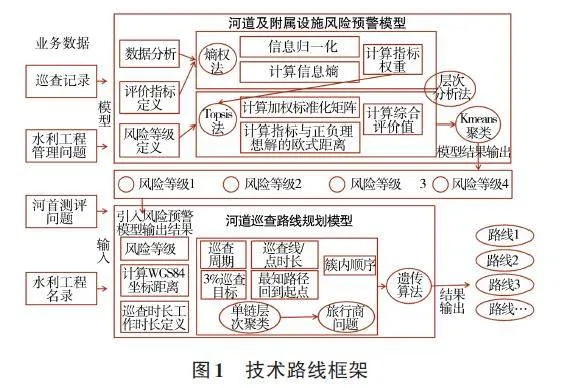
本研究首先通过熵权-Topsis方法确定水利工程设施风险等级,然后通过遗传算法求解最优巡查路线,具体技术路线框架,见图1。
3 模型建立
3. 1 风险预警模型
本次河道水利工程设施风险评估模型主方法采用熵权-Topsis方法[13]计算风险权重和巡查对象风险等级,利用层次分析法(Analytic HierarchyProcess,AHP)进行调权拟合,增强模型泛化使用效果,进一步用K-means无监督学习方法[14-15]计算出河道及附属设施风险等级划分结果。
河道及附属设施风险预警模型通过对风险等级进行分类,定义风险等级分别为一般风险(1级)、较大风险(2级)、重大风险(3级)、特大风险(4级)。不同的风险等级对应的标识定义,见表1。
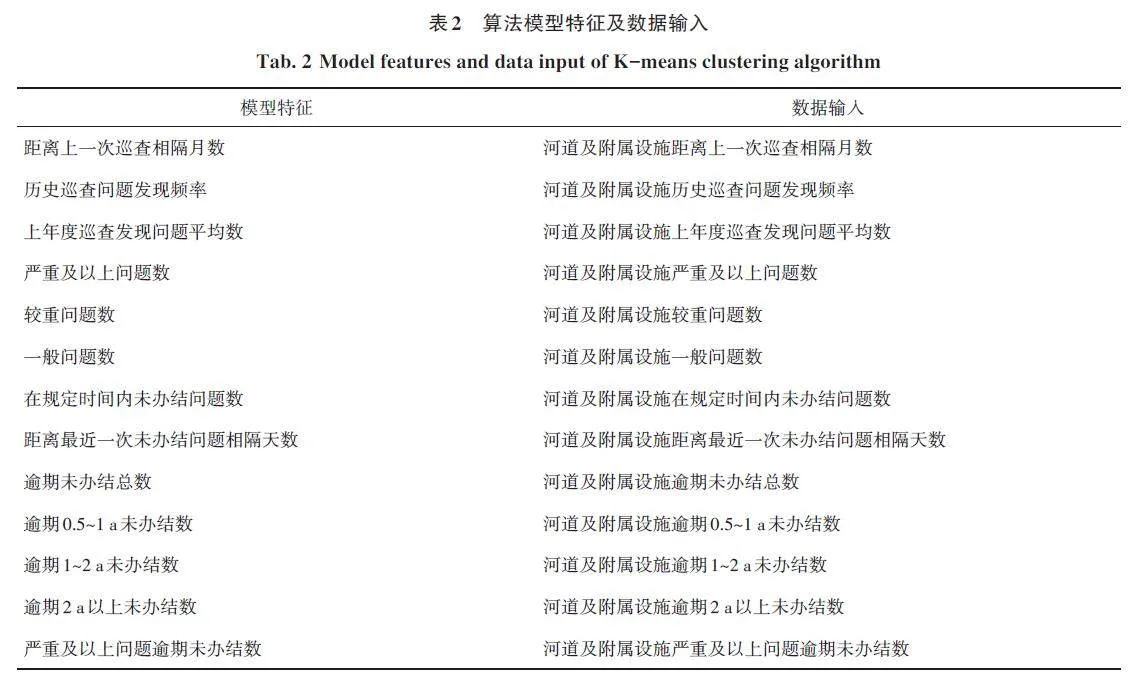
风险预警模型通过河道及附属设施巡查发现的历史问题数据,定义风险相关评价指标,计算各评价指标的信息熵,确定指标权重,以关联河道堤防、水闸、泵站的空间位置为建模特征、河道及附属设施风险等级为标签的模型训练数据,通过聚类算法,进一步计算风险评价分值,最后通过聚类算法划分巡查对象的风险等级。模型中K-means 聚类算法模型特征及数据输入,见表2。
3. 2 巡查路线规划模型
本次研究中,根据水利工程风险等级、巡查频率、巡查时长、水利工程地理空间分布等因素,应用遗传算法(Genetic Algorithm),求解河道巡查路线规划问题。遗传算法是一种模拟自然进化过程的优化算法,其原理基于达尔文的进化论和遗传学理论,它通过模拟自然界中的遗传操作,逐代进化搜索解空间中的最优解。本研究中,应用遗传算法流程如下。
a)初始化种群。首先,生成一个初始的种群,其中每个个体代表问题的一个潜在解。这些个体可以通过随机生成、或者根据先验知识创建,每个基因对应1个参数值,初始化t←0进化代数计数器,随机生成M 个个体作为初始群体P(t),例如x1、x2、x3等。
b)适应度评估。对于每个个体,定义一个适应度函数来评估其在解空间中的优劣程度,计算P(t)中各个个体的适应度值。
c)选择操作。通过选择操作,从当前种群中选择一部分优秀的个体作为父代用于繁殖下一代。
d)交叉操作。在交叉操作中,从选择的父代中选择2个个体,通过某种方式对它们的基因进行交叉,生成新的个体。交叉的方式可以是单点交叉、多点交叉、均匀交叉等。
e)变异操作。变异操作是为了引入种群中的多样性,防止陷入局部最优解。在变异操作中,对新生成的个体进行基因的随机变化,通常是通过随机改变某些基因值或位置,并通过以上运算得到下一代群体P(t+1)。
f)形成新种群。通过选择、交叉和变异操作,形成新的种群。新种群中包含父代中的一部分个体以及通过交叉和变异操作生成的新个体。
g)重复迭代。重复进行选择操作、交叉操作、变异操作、形成新种群,直到满足终止条件。终止条件可以是达到一定的迭代次数、找到满意的解,或者适应度达到某个阈值等。
h)输出结果。输出最优解及其适应度值。
4 模型实践与应用
4. 1 风险预警模型应用
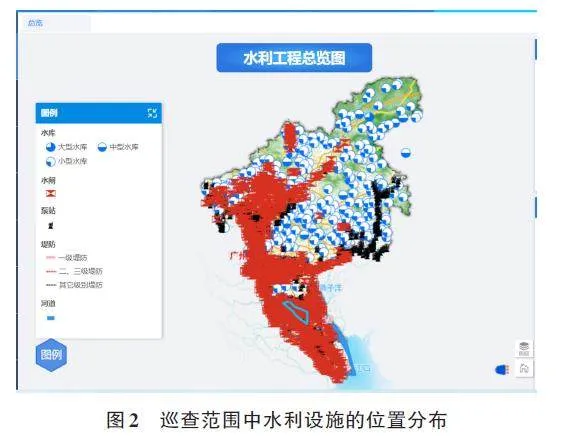
本次研究中,针对广州市河涌监测中心河道巡查范围内1 817条河道、3 273个堤防、1 177个水闸、868个泵站、298座水库作为巡查对象,巡查范围内水利设施的位置分布,见图2。
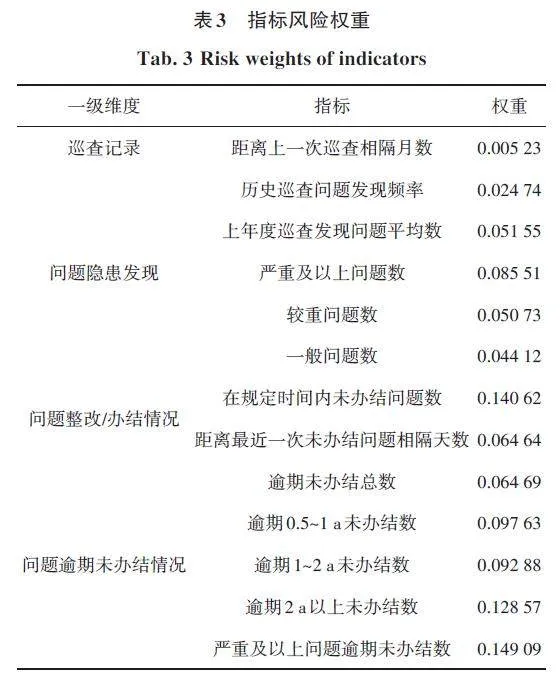
按照每月选取总量3%的设施进行巡查,对上述水利工程设施数据及历史问题数据进行业务属性分析。其中,业务属性以四大维度进行分类,分别为巡查记录、问题隐患发现、问题整改/办结情况及问题逾期未办结情况。在四大维度基础上,定义13个评估指标指标,分别为距离上一次巡查相隔月数、历史巡查问题发现频率、上年度巡查发现问题平均数、严重及以上问题数、较重问题数、一般问题数、在规定时间内未办结问题数、距离最近一次未办结问题相隔天数、逾期未办结总数、逾期0. 5~1 a未办结数、逾期1~2 a未办结数、逾期2 a以上未办结数、严重及以上问题逾期未办结数。各指标权重,见表3。
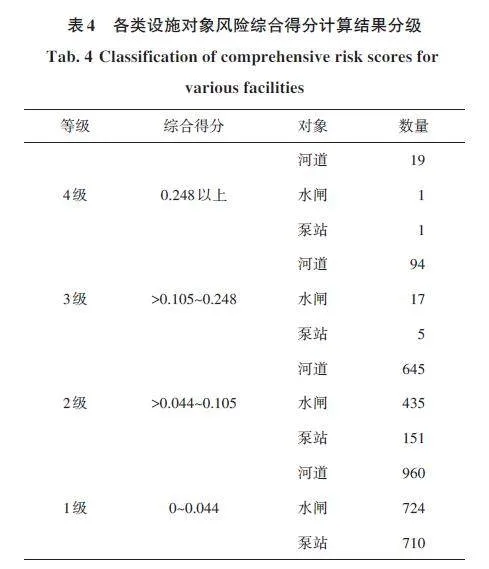
本次研究中,预先设定的4个类别数量,采用熵权-Topsis 方法对上述13 个指标进行风险权重计算。根据获得的标准化矩阵和各指标权重计算加权标准化矩阵,通过定义正负理想解(正理想解和负理想解分别为各指标在标准化矩阵中的最大值和最小值),分别计算评价对象各评价指标与正负理想解的欧氏距离。根据各评价对象与正负理想解的距离即相对接近程度,计算综合评价值得到风险评价分值,再利用层次分析法[16]进行调权拟合,从而增强模型泛化使用效果。再通过K-means 无监督学习方法计算出每个类别的数据中心,Kmeans算法通过最小化每个类别内数据点的方差,即将数据点与其所属类别中心的距离最小化,以确保每个数据点都属于距离其最近的类别中心为目标进行迭代,得出对应于4个类别的聚类结果以及其分值划分范围,分别为:0~0. 044、>0. 044~0. 105、>0. 105~0. 248、0. 248以上。计算结果见表4。
结合水利工程GIS空间位置信息与风险等级对应的标识定义,生成河道水利工程设施风险评估计算结果分布,见图3。
4. 2 巡查路线规划应用
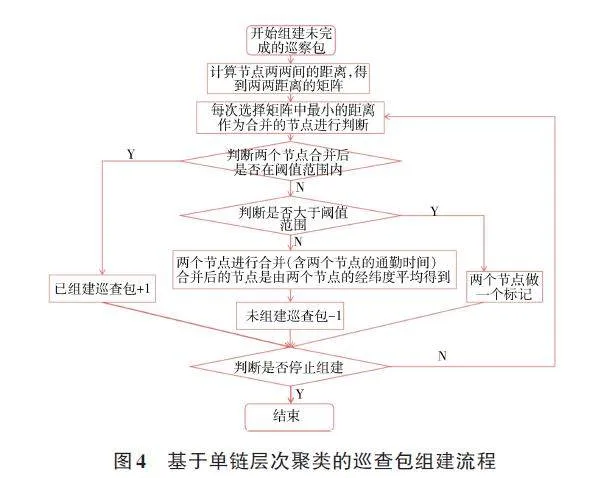
首先通过结合根据水利工程风险等级,水利工程地理空间分布等因素,采用单链层次聚类的方法组织巡查任务包。研究中,依托单链层次聚类方法,根据输入模型数据中的各个巡查对象经纬度坐标信息计算巡查对象两两之间的距离,得出两两距离矩阵,选择矩阵中最小距离巡查对象纳入最大最小时长阈值判断。把小于最小阈值巡查对象进行合并,形成新对象,然后将合并前的2个巡查对象巡查通勤时间进行累计,且经纬度取2个对象平均值,得出的新巡查对象将纳入到下一轮的为组建巡查包库,参与下一轮巡察包组建。当巡查对象合并后在最大最小阈值判断范围内,则组建巡察包。当在大于最大阈值则进行标记,并在下次不进行合并计算。基于已经组建好的巡查任务包进行线路规划,以寻找最优的路径为目标,找到一条最短路径,以最小的成本或时间完成巡查任务。
在河涌巡查线路规划中,可能存在巡查时间窗口、巡查点的访问限制等约束,将巡查点表示为图的节点,巡查路径表示为边,构建图模型。在给定的约束条件下,通过找到最优的组合或排列来达到最优解,并用遗传算法构建巡查路线,输出巡查包里的顺序路线。动态组织巡查任务包流程见图4。
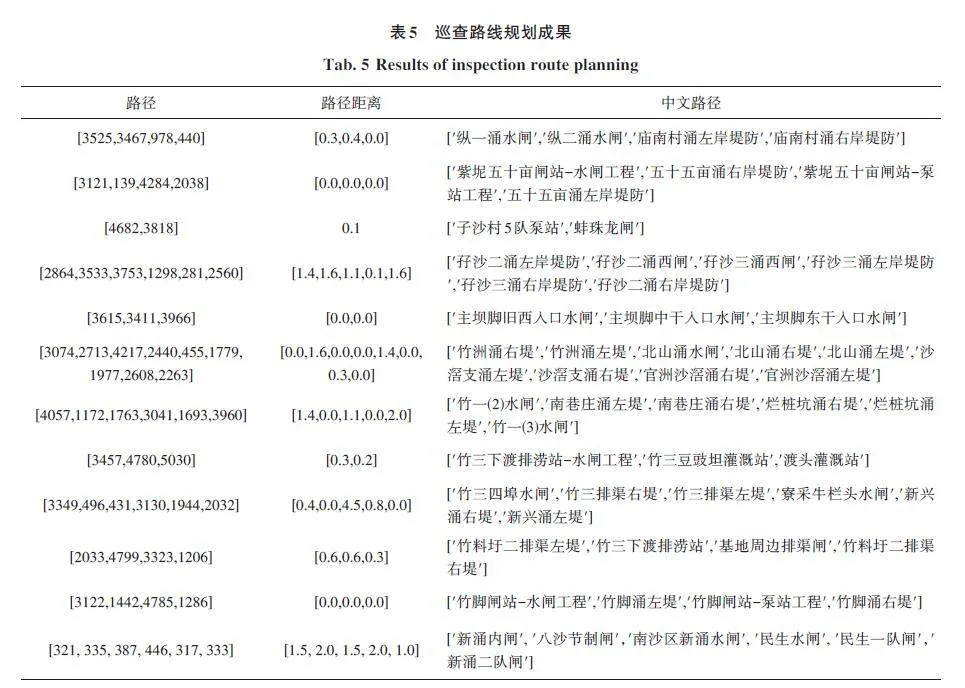
基于已经组建好的巡查任务包进行巡查线路规划,将其转化为旅行商问题寻找最优的路径[8]。本项目实际应用中,以找到一条成本最小或时间最短的巡查路线为目标,使用遗传算法[7]对上述问题进行求解,对5 318个巡查点组建成的1 110个巡查任务包,成功规划巡查路线,部分结果见表5。
训练线路规划采用一种启发式方法以生成巡查最短路径,按照上述动态组织巡查任务包流程方式初始化巡查人员自定义参数包括人员单日工作时长、行进速度、单个工程巡查耗时、距离计算即两两水利工程的经纬度进行换算出地表距离,采用层次聚类,最终输出最短巡查线路任务包列表。
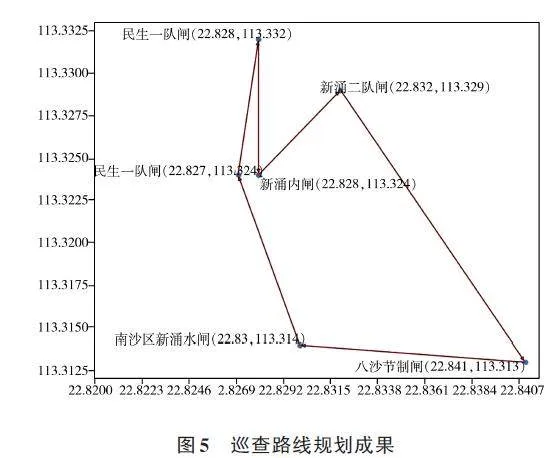
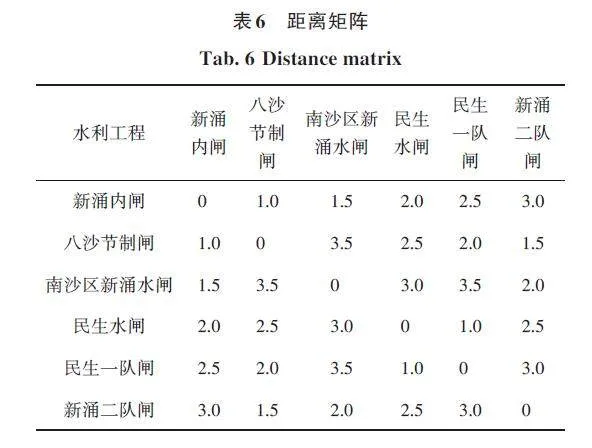
以表5里最后1条路线规划为例:'新涌内闸', '八沙节制闸','南沙区新涌水闸','民生水闸','民生一队闸','新涌二队闸',两两水利工程相隔距离矩阵,见表6。
通过使用遗传算法求解该问题的最短巡查线路得出最短路径为:'新涌内闸','新涌二队闸','八沙节制闸','南沙区新涌水闸','民生水闸','民生一队闸'。该最短路径的路径长度为8 km,该最短路线规划成果,见图5。
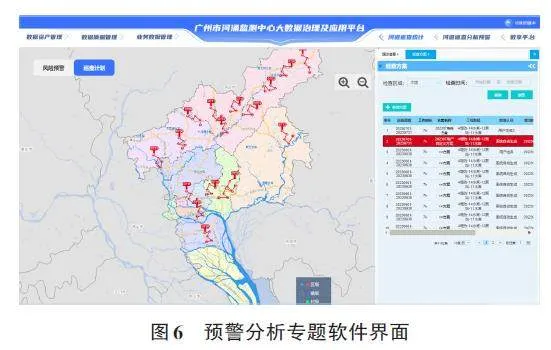
最终形成预警分析专题软件。将河道巡查的风险等级、巡查路线、巡查计划等模型结果结合地理空间能力以及实际业务需求,构建预警分析专题,解决巡河过程中巡查覆盖面不足、人工排班、随机抽取巡查对象等问题,形成具有界面化的软件,软件界面效果见图6。
5 结论与分析
本文基于风险预警-遗传算法耦合的方法,对广州市河涌监测中心河道巡查范围内水利工程设施进行了风险分级,通过单链层次聚类针对5 318个巡查点组建成1 110个巡查任务包,最后采用遗传算法成果求解最优巡查路线。实际应用中,基于求解的最优巡查路线,广州市河涌监测中心累计开展巡查730次,上报问题744个,已办结126个,帮助巡查人员有针对性地巡查高风险区域和关注重点问题,减少巡查盲区,减少了不同巡查对象路线耦合造成的路线重复巡查频次,减轻了巡查人员的工作负担,对河道基层管养的减负增效有积极帮助,可为传统的河道巡查管理工作提供新的尝试与思路。
参考文献:
[1] 边锦华,张晓霞. 求解TSP问题的一种变领域遗传算法[J]. 福建电脑,2023,39(12):24-27.
[2] 王建忠,唐红. TSP问题的一种快速求解算法[J]. 微电子学与计算机,2011,28(1):7-10.
[3] CINAR A C,KORKMAZ S,KIRAN M S. A discrete tree-seed algorithm for solving symmetric traveling salesman problem[J].Engineering Science and Technology, an International Journal,2020, 23(4): 879-890.
[4] ZHANG Z, HAN Y. Discrete sparrow search algorithm for symmetric traveling salesman problem [J]. Applied Soft Computing, 2022,118. DOI: 10. 1016/j. asoc. 2022. 108469.
[5] SKINDEROWICZ R. Improving ant colony optimization efficiency for solving large TSP instances[J]. Applied Soft Computing, 2022,120. DOI: 10. 1016/j. asoc. 2022. 108653.
[6] 李彦强,王建辉. 基于遗传算法的无人机编队高速公路巡检任务规划方法[J]. 市政技术,2023,41(11):67-73.
[7] 张大威,张明广,刘文浩,等. 基于栅格遗传算法的采购供应物流配送车辆路线规划方法[J]. 物流科技,2023,46(6):4-7.
[8] 史健. 基于改进遗传算法的鲜活农产品物流配送规划方法研究[J]. 佳木斯大学学报(自然科学版),2023,41(3):151-155.
[9] 赵力萱,吴泽驹,何康园,等. 碳减排背景下定制公交路线规划方法[J]. 交通运输研究,2022,8(3):56-65.
[10] 王勇臻,陈燕,于莹莹. 求解多旅行商问题的改进分组遗传算法[J]. 电子与信息学报,2017,39(1):198-205.
[11] 张硕航,郭改枝. 多旅行商模型及其应用研究综述[J]. 计算机科学与探索,2022,16(7):1516-1528.
[12] 许林涛. 丹山拦河闸止水工程系统风险评价技术研究[J]. 水利技术监督,2021(6):223-227.
[13] 王莉芳. 基于组合赋权与灰色改进TOPSIS方法的受灾点应急物质需求紧迫性分级评价[J]. 安全与环境工程,2017,24(6):94-100.
[14] 张嘉龙. 基于相异度与邻域的K-means初始聚类中心选择算法[J]. 计算机时代,2021(8):57-59,62.
[15] 吴海丽. 大数据挖掘中的K-means 无监督聚类算法的改进[J]. 现代电子技术,2020,43(19):118-121.
[16] 王金凤,韦鹏,马飞. 层次分析法在应急预案事故灾难类风险评估中的应用[J]. 质量与认证,2024(1):50-52.
(责任编辑:李燕珊)
