单节理深埋隧洞开挖瞬态卸荷响应机理数值模拟研究

摘 要：采用颗粒流数值模拟重现深埋单节理隧洞瞬态卸荷过程，从应力状态、变形特征、裂纹扩展等多角度探析节理特征对双江口水电站进厂交通洞瞬态卸荷效应的影响，研究表明：节理对深埋隧洞瞬态卸荷的应力调整过程有着重要的影响，应力集中区将由硐室底角、拱顶转移至节理尖端。随着节理长度的增加，节理尖端应力集中区域离自由面距离逐渐增大，围岩损伤区逐步向岩体深部发生迁移。不同节理角度下，微裂纹数目差异性显著，其中60°和30°节理围岩中的微裂纹数量较多；此外，压剪裂纹所占比例随着节理角度的增大呈现先增大后减小的变化趋势，45°时达最大。研究成果对水工隧洞开挖卸荷作用下围岩破坏机制认识和评价具有指导意义。

关键词：深埋隧洞；节理岩体；瞬态卸荷；裂纹扩展

中图分类号：TV554 文献标识码：A 文章编号：1001-9235（2024）09-0074-09

深部岩体常含有节理、节理甚至大断层等不同程度的结构面，这类缺陷很大程度上决定了岩体的强度，当遭受高地应力和卸荷等外荷载作用时，促使围岩破裂损伤加剧，结构面缺陷扩展、贯通至岩体失稳破坏［1-3］。岩石（体）在外力作用下的变形及达到承载强度后的破坏失稳现象归根到底是能量驱动下岩石内部裂纹萌生、扩展、凝聚、贯通的结果［4-6］。因此，从能量转化、裂纹演变等角度探析深埋节理隧洞的瞬态卸荷效应有着重要意义。

自然界岩体由结构面（节理、裂隙等）与岩块两部分组成，非贯通节理广泛赋存于隧洞岩体中［7］。而隧洞围岩单元在开挖前后的应力状态经历了“三向主应力状态→单面开挖卸载→切向应力集中”的变化过程。岩体的地质结构及构造的复杂性，导致节理围岩在瞬态卸荷作用下表现出更为复杂的力学行为。对此，相关学者进行了大量的研究。Liu等［7］采用单轴开洞试验，对隧洞的应力和裂缝分布进行了理论分析，结果表明节理位置对隧洞整体承载力影响较大，隧洞周围的裂缝分布与节理位置和应力集中系数密切相关；周喻等［8］通过试验和计算对比，研究了单侧限压缩条件下裂隙岩体强度、裂纹分布及裂纹演化规律形成机制；周辉等［9］、Liu等［10］利用相似材料的直剪试验分析了结构面对岩爆发生的触发机制，并通过试验解释了断层滑移型岩爆的机制和岩爆发生的前兆信息。随着计算机技术的发展，数值计算方法在岩爆模拟分析中得到了广泛应用。Feng 等［11］采用组合式有限元方法ELFEN，通过考虑结构面倾角、位置和侧压系数的参数分析，揭示了卸荷条件下结构面对圆形隧洞的力学响应；Abdul等［12］通过FLAC3D显式程序模拟了小尺度剪切平面结构对隧洞边界产生破坏作用；吴文平等［13］指出应变型岩爆的发生与隧洞的开挖尺寸有一定的关系，通过FLAC3D再现了锦屏II级水电站引水隧洞单节理围岩岩爆破坏过程，指出了在低应力条件下，结构面自身的变形与破坏对围岩稳定起主要作用；Zhang等［14］通过FLAC模拟研究发现，结构面的存在阻碍了围岩应力向深部岩体调整的过程，导致开挖边界至结构面之间的岩体应力集中和能量不断积聚。可见，目前节理在不同应力状态下的影响方面研究已取得了大量成果，但无法体现在开挖卸载作用下，穿节理隧洞围岩破裂演化机理，且从细观裂纹扩展角度对穿节理隧道开挖面失稳机理的模拟研究相对较少。因此，构建穿节理隧洞的精细化模型以进一步开展深入研究是十分必要的。

本文以双江口水电站隧洞为研究背景，采用颗粒流数值模拟重现深埋单节理隧洞瞬态卸荷过程，从应力状态、变形特征、裂纹扩展和能量转换等多角度探析节理特征对深部岩体瞬态卸荷效应的影响，为隧道穿越断层带等不良地质体时隧道开挖面稳定性评价、开挖面失稳预警及支护措施的优化提供理论依据。

1 深埋单节理隧洞颗粒流模型

1. 1 双江口工程概况

隧址区地面标高3 260～5 500 m，高差达2 300m，为典型的高山峡谷地貌。隧道最大埋深约为2 080 m，开挖断面的当量直径为11 m。工程区岩性单一，大部分为第三系中粒角闪黑云花岗岩（E2R），隧道区围岩岩体较为完整，以Ⅱ、Ⅲ类围岩为主，具有储存高弹性应变能的能力。

1. 2 接触本构模型

颗粒流数值模拟是一种离散分析单元法，能将任意岩石形态构造成颗粒集合体，通过颗粒之间的相互作用对岩石的宏观力学属性进行仿真，并通过颗粒间黏结的断裂来模拟岩石材料裂纹的产生。本文以平直节理（Flat-Joint）接触模型为基础，Flat-Joint接触模型与平行黏结模型、接触黏结模型最大的区别在于能够抑制颗粒黏结破坏后的旋转［15］，颗粒形状构造成多边形并相互“咬合”在一起，当颗粒黏结破坏后由于颗粒之间的相互“咬合”作用，颗粒单元无法发生自由旋转运动，只能整体间滑动或脱落，与实际岩石材料内部微观构造更为接近。

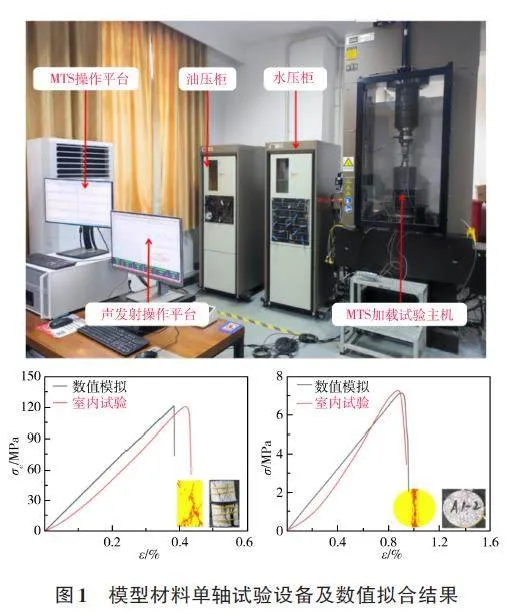
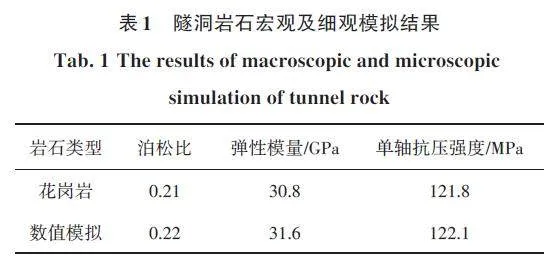
采用Flat-Joint接触模型为本构关系的完整岩石材料数值模型，其可以更加真实地反映岩石材料的宏观力学特性，通过设置相应的节理单元来建立节理岩石数值模型。图1所示，岩石细观参数采根以模型试样室内试验的模拟应力-应变曲线和破坏形态为参照，通过“试错法”得出黏结颗粒模型相对应的细观物理力学性质参数［16］，模拟试验的弹性模量、泊松比与室内试验值吻合较好，见表1、2。隧洞岩体节理单元模拟采用Smooth-Joint接触模型进行设置，而节理的力学参数低于完整岩石的力学参数。可根据节理的力学参数比完整岩石的力学参数小1%～20%进行选取［17］，见表3。

1. 3 颗粒流模型

隧洞结构边界是半无限体边界，而颗粒流程序无法对如此大范围的岩石材料模型进行数值模拟，且隧洞开挖对于距离远的岩体影响微乎其微。因此，在数值模拟中会选取有限的计算范围建立模型，该计算范围只要大于隧洞开挖的影响范围即可。大量工程经验表明，隧洞结构的影响范围一般在距隧洞中心3～5倍的隧洞特征尺寸内。以双江口水电站交通洞为研究背景，模拟隧洞瞬态卸荷过程，设置模型计算范围为26 m×26 m，硐室边墙高为2 m，底宽4 m，拱高2 m，硐室置于模型中心，隧洞中心与计算模型中心重合。通过删除隧洞结构范围内的颗粒模拟瞬态卸荷，建立数值模型，见图2。

本文从节理长度、角度、位置等方面展开研究，分析深埋洞室瞬态卸荷过程中，节理围岩应力分布状态、围岩变形规律和破坏特征等。双江口水电站引水隧洞围岩中垂直向地应力与水平向相差较小，主应力值平均20 MPa左右，因此在数值模拟中，通过PFC2D内置的Fish语言和伺服原理编写模型仿真程序，通过对上下边界墙和左右边界墙施加20 MPa围压模拟地应力作用，并在程序伺服系统下通过不断调整边界墙的位移速率实现恒定围压，隧洞瞬态卸荷则通过导入洞室结构并删除开挖面范围内颗粒实现。

1. 4 工况设计

为了研究节理长度和倾角对隧洞瞬态卸荷效应的影响，考虑到对围岩破坏特性影响较大的水平贯通节理，根据不同节理长度L 可分为6种工况，分别为5、6、7、8、9、10 m，节理中心与模型几何中心重合并贯穿隧洞，具体设置情况见图3a；基于隧洞结构及计算模型尺寸考虑，选取长度为6 m的贯通节理，节理中心与隧洞结构几何中心重合并贯穿隧洞，通过改变节理所在面与水平X 轴的夹角α 来探究不同节理角度对深埋隧洞瞬态卸荷效应的影响。其中α 依次设置为0°、30°、45°、60°和90°，见图3b。其中，初始状态下节理水平分布，瞬态卸荷时隧洞开挖面范围内的节理也随之瞬态破坏，每种工况下开挖过程均计算50 000步。

2 数值计算结果与分析

2. 1 节理长度对深埋隧洞瞬态卸荷效应的影响

2. 1. 1 变形演化规律

在隧洞开挖过程中，围岩的位移直接影响到隧洞结构的破碎程度，也是衡量围岩稳定性的一个重要指标。不同节理长度瞬态卸荷下围岩内位移变化情况大致相同，以6 m节理长度的数值模型为例分析，围岩中位移方向见图4。

从中可以看出，节理围岩表现出的自我调整主要体现在3个方面：①拱顶处围岩呈下沉趋势，但拱肩围岩相向运动的同时有向中央处挤压的趋势，形成“起拱”效应，从而提高了拱顶的承载能力；②两帮及左右底角处围岩表现出相向运动的趋势，从而使整个隧洞结构受力趋于均衡，避免局部发生较大变形破坏；③拱底板部位围岩相互挤压呈现抬升趋势。

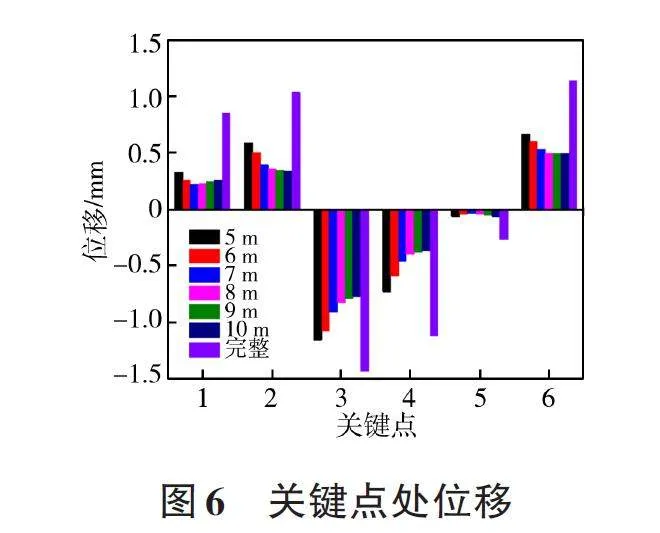
为进一步探究隧洞结构变形规律，在隧洞模型左右底角、左右拱肩、拱顶以及底板中央等关键点位置设置了图5所示的6个测量单元，进行围岩位移监测。

图6为各关键点处颗粒位移情况，由图可知各关键点处完整围岩位移均要大于节理围岩位移，且在关键点5处完整围岩位移超过节理围岩最大位移的4. 5倍，这是因为水平贯穿节理的存在，使得隧洞围岩损伤变形范围加大，隧洞轮廓周边围岩位移相对减小。不同节理长度下，同一关键点处位移整体上随节理长度的增加而逐渐减小并趋于稳定。相同节理长度下，各关键点处位移有较大区别，关键点2与点4处围岩位移始终相差较小，而关键点1与点5处围岩位移相差相对较大，点1处位移皆大于点5处。所有关键点中，点3处位移始终最大，点5处位移一直最小。关键点3 处围岩位移大于点6处，但差值随着节理长度的增加而不断减小，从5 m节理到10 m节理，两者差值减小了近43. 3%，说明在不同长度水平贯通节理围岩中，拱顶位移始终大于底板位移，但差值随节理长度递减。

2. 1. 2 裂纹扩展规律

图7为不同节理长度下隧洞围岩微裂纹分布，其中，黑色线条代表细观压剪裂纹，绿色线条代表细观拉伸裂纹，微裂纹主要集中分布在隧洞结构周边，裂纹的萌生、扩展、积聚和交叉等使围岩结构劣化、力学特性弱化。应力重分布过程中，由于开挖面法向卸荷，引起围岩切向应力集中，使得在平行于开挖面方向发生压剪型裂纹扩展，导致围岩压剪破坏。深埋隧洞瞬态卸荷后，围岩以压剪破坏为主，对应于图中黑色剪裂纹占主导地位；完整围岩剪裂纹集中分布在底板和两帮附近，而左右底角处有少量拉裂纹分布。不同节理长度下围岩微裂纹分布情况有较大差异，节理长度较小时，裂纹分布较密集且主要在底板、两帮和拱肩处；节理长度较大时，裂纹分布较稀疏但延伸的范围较大，底板和拱顶附近有少量裂纹积聚，两帮区域内裂纹零星分布并向初始节理尖端延伸。由此可知，随着节理长度的增加，节理尖端应力集中处离自由面距离逐渐增大，围岩损伤范围不断扩展，使隧洞两帮内微裂纹分布逐渐变得稀疏，延伸的区域范围逐渐变大，围岩损伤区域逐步向深部迁移。

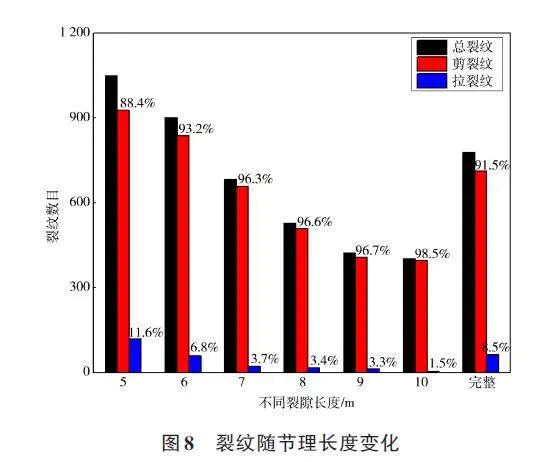
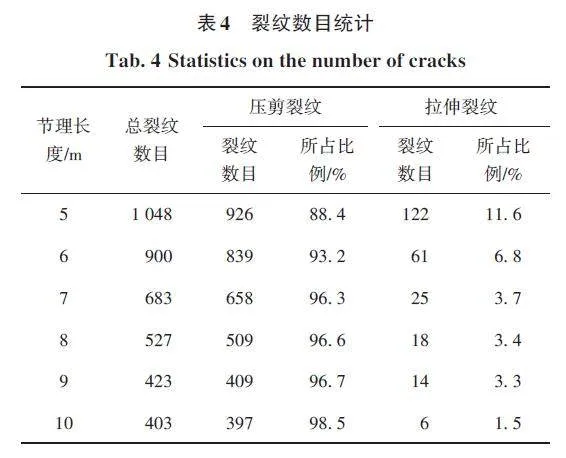
围岩损伤破坏时，拉、剪裂纹表征不同的破坏机理，细观裂纹数目统计数据见表4，根据表中数据对比分析不同节理长度下裂纹数目及各裂纹所占比例见图8。不同节理长度下，微裂纹总数和拉剪裂纹所占比例各不相同，节理长度较小（5、6 m）时，节理围岩中微裂纹总数要多于完整围岩，而其余节理长度下围岩中微裂纹总数低于完整围岩。其中节理长度为5 m时，剪裂纹所占比例为88. 4%，低于完整围岩剪裂纹所占比例91. 5%，其他节理长度下剪裂纹所占比例要高于完整围岩。整体上随着节理长度的增加，微裂纹总数呈现单调递减的趋势，从1 048条降至403条，降幅高达62%；剪裂纹所占比例随节理长度单调递增，从最低值88. 4%上升到最高值98. 5%，上升幅度为11. 4%。

2. 2 节理倾角对深埋隧洞瞬态卸荷效应的影响

2. 2. 1 变形演化规律

颗粒流程序中，模型颗粒的位移分布可近似表示隧洞围岩的位移场，不同节理角度下围岩位移情况见图9，节理角度不同，隧洞围岩位移场也大不相同。其中，完整围岩中位移场分布较为对称，隧洞两帮极小范围内位移较大，而底板下扇形区域内位移相对较小。0°节理围岩中位移场分布均匀，只在隧洞拱顶和边墙较小区域上出现较大位移。30°节理围岩中，节理尖端附近出现较大位移，且左上侧扇形区域位移较大，右侧边墙由于受节理影响较大而变形严重，围岩位移也较大。45°节理围岩中，隧洞结构左侧围岩出现大的变形，左上侧月牙形范围内位移较大，而底板下扇形区域位移很小。60°节理围岩中靠近节理尖端的拱顶围岩位移较大，出现颗粒脱落，底板下三角形区域内位移相对较小。90°围岩中隧洞底角处变形相对严重，位移较大，拱顶上侧弧形区域位移也较大，而底板下半圆弧形范围内位移相对较小。整体上，隧洞围岩位移随节理倾角的改变而同步迁移，但底板下围岩位移始终较小。

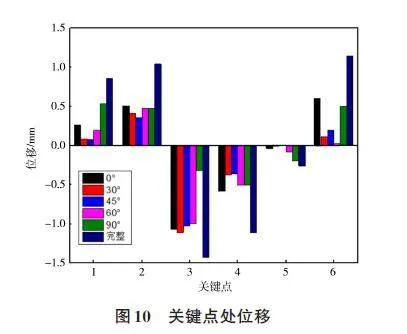
不同节理角度关键点位移情况见图10，由图可知，节理围岩各关键点位移均小于完整围岩位移。关键点3 处，30°节理围岩位移达到最大值1. 11mm，低于完整围岩点3处位移近22. 4%。相同节理角度下，各关键点处围岩位移差距较大，0°、30°、45°和60°节理围岩在点3处发生最大位移，而90°节理围岩则在点1处位移最大，这是因为90°节理竖直贯穿拱顶，对拱顶上方围岩结构影响较大，导致隧洞拱顶处变形不明显。随着节理角度的增大，关键点1、2、4、5处围岩位移呈现出先减小后增大的趋势；关键点3处围岩位移则先增大后减小；关键点6处围岩位移方向发生改变，0°和90°中位移向下，其他角度中位移则向上，说明在斜节理影响下，隧洞底板“起拱”效应明显。关键点2、4、6处，0°节理围岩位移取最大值，关键点1、5处，90°节理围岩位移达到最大，关键点3处，最大围岩位移发生在30°节理围岩中，关键点5围岩位移始终最小。

2. 2. 2 裂纹扩展规律

图11为不同节理角度下围岩中微裂纹分布情况，图中占主导地位的黑色裂纹为压剪裂纹，相对较少的绿色裂纹为拉伸裂纹，拉裂纹多在底角处分布，而剪裂纹环形分布于隧洞结构周边区域。与完整围岩中微裂纹分布形态相比，不同角度节理围岩中微裂纹分布范围更为广阔，距离隧洞轮廓较远，且大都在节理两侧沿隧洞周边散落分布，表明围岩损伤区域随节理倾角同步发生迁移。节理角度不同，围岩中微裂纹分布形态有所差异，随着节理角度增大，隧洞两帮附近围岩内的微裂纹逐渐变得稀少，而底板下区域围岩中微裂纹逐渐增多；斜节理（30°、45°和60°）围岩中，微裂纹分布相对密集，而0°和90°节理围岩中微裂纹分布区域相对分散。

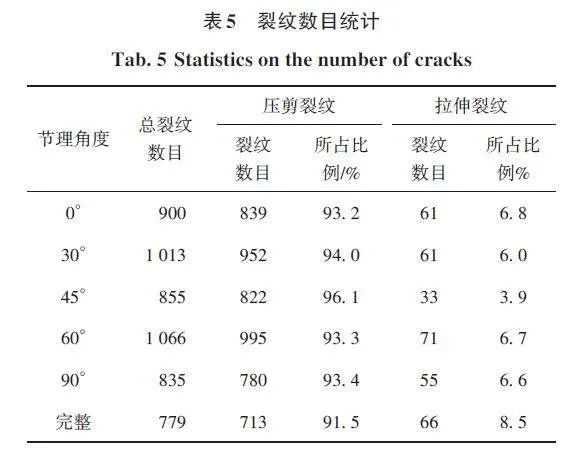
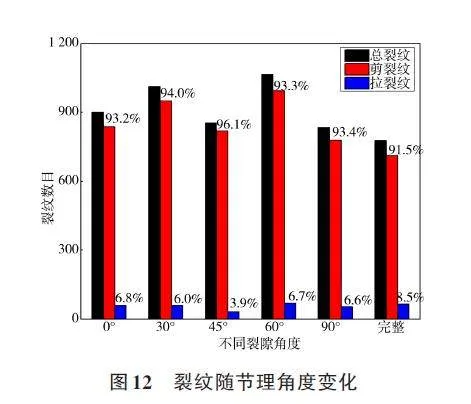
不同节理角度下隧洞围岩损伤过程中细观裂纹数目统计见表5，由表中数据可知，微裂纹中，剪裂纹数目要远远多于拉裂纹，表明隧洞瞬态卸荷过程中，围岩发生压剪破坏居多。对比分析各裂纹总数及所占比例见图12，不同节理角度下围岩中微裂纹总数和剪裂纹数都要多于完整围岩，60°节理围岩中微裂纹总数达到最大值1 066条，高于完整围岩中微裂纹总数近37%，同时比90°节理围岩中微裂纹总数最小值835条要多28%左右。不同节理角度下，微裂纹数目变化较大，其中60°和30°节理围岩中微裂纹总数较多，0°节理围岩次之，而45°和90°节理围岩中微裂纹总数相对较少。压剪裂纹所占比例随着节理角度的增大呈现出先增大后减小的变化趋势，但都要高于完整围岩，在45°节理围岩下，压剪裂纹所占比例达到最大值96. 1%。

3 结论

为探究节理分布对深埋隧洞瞬态卸荷效应的影响，对不同节理长度、角度、位置等工况进行数值仿真。从隧洞围岩应力特性、变形规律、裂纹扩展特征及能量转化规律等方面进行分析，得出的主要结论如下：①深埋隧洞瞬态卸荷的应力调整过程有着重要的影响，节理的存在迫使隧洞开挖后应力调整的区域发生改变，不同长度水平贯通节理围岩中，拱顶位移始终大于底板位移，但差值随节理长度递减；②随着节理长度的增加，节理尖端应力集中处离自由面距离逐渐增大，围岩损伤范围不断扩展，使隧洞两帮内微裂纹分布逐渐变得稀疏，延伸的区域范围逐渐变大，围岩损伤区域逐步向深部迁移；③不同节理角度下，微裂纹数目变化较大，其中60°和30°节理围岩中微裂纹总数较多，0°节理围岩次之，而45°和90°节理围岩中微裂纹总数相对较少，压剪裂纹所占比例随着节理角度的增大呈现出先增大后减小的变化趋势，但都要高于完整围岩，在45°节理围岩下，压剪裂纹所占比例达到最大值96. 1%。

参考文献：

［1］ PETRUZALEK M， VILHELM J， RUDAJEV V， et al.Determination of the anisotropy of elastic waves monitored by asparse sensor network ［J］. International Journal of RockMechanics and Mining Sciences， 2013， 60：208-216.

［2］ WANG S F， HUANG L Q， LI X B. Analysis of rockbursttriggered by hard rock fragmentation using a conical pick underhigh uniaxial stress［J］. Tunnelling and Underground SpaceTechnology Incorporating Trenchless Technology Research， 2020，96. DOI：10. 1016/j. tust. 2019. 103195.

［3］ ZHOU Y X， XIA K， LI X B， et al. Suggested methods fordetermining the dynamic strength parameters and mode-I fracturetoughness of rock materials［J］. International Journal of RockMechanics and Mining Sciences， 2011，49：105-112.

［4］ CHEN D， WANG E Y， LI N. Analyzing the rules of fracture anddamage， and the characteristics of the acoustic emission signal ofa gypsum specimen under uniaxial loading［J］. Journal ofGeophysics and Engineering， 2017，14（4）：780-791.

［5］ LIU G H， LIU Z T， FENG J J， et al. Experimental research onthe ultrasonic attenuation mechanism of coal［J］. Journal ofGeophysics and Engineering， 2017，14（3）：502-512.

［6］ XIE H P， PENG R D， JU Y， et al. On energy analysis of rockfailure［J］. Chinese Journal of Rock Mechanics and Engineering，2005，24（15）：2603-2608.

［7］ LIU X Q， WANG G， SONG L B ， et al. A new rockburstcriterion of stress–strength ratio considering stress distribution ofsurrounding rock［J］. Bulletin of Engineering Geology and theEnvironment，2022，82（1）. DOI：10. 1007/s10064-022-03042-x.

［8］ 周喻，孙铮，王莉，等. 单侧限压缩下预制裂隙试样力学特性及板裂化机制细观研究［J］. 岩土力学，2018，39（12）：4385-4394.

［9］ 周辉，孟凡震，张传庆，等. 结构面剪切破坏特性及其在滑移型岩爆研究中的应用［J］. 岩石力学与工程学报，2015，34（9）：1729-1738.

［10］ LIU W R， XU J， WANG Z， et al. Experimental research on damage characteristics and safety damage threshold of jointedcaverns based on acoustic emissions［J］. Geomechanics andGeophysics for Geo-Energy and Geo-Resources， 2021， 7（3）.DOI：10. 1007/s40948-021-00270-5.

［11］ FENG F， LI X B， ROSTAMI J， et al. Modeling hard rock failureinduced by structural planes around deep circular tunnels［J］.Engineering Fracture Mechanics， 2018， 205： 152-174.

［12］ ABDUL M， HAFEEZUR R， MUHAMMAD Z， et al. Impact ofShear Zone on Rockburst in the Deep Neelum-Jehlum HydropowerTunnel： A Numerical Modeling Approach［J］. Energies， 2018，11（8）. DOI：10. 3390/en11081935.

［13］ 吴文平，冯夏庭，张传庆， 等. 深埋硬岩隧洞围岩的破坏模式分类与调控策略［J］. 岩石力学与工程学报，2011，30（9）：1782-1802.

［14］ ZHANG C， FENG X T， HUI Z， et al. Rockmass damagedevelopment following two extremely intense rockbursts in deeptunnels at Jinping II hydropower station， southwestern China［J］.Bulletin of Engineering Geology and the Environment ， 2013 ，72（2）： 237-247.

［15］ LUO Y， WANG G， LI X P， et al. Research on triaxialcompression failure characteristics and meso-simulation of brittlegypsum material［J］. European Journal of Environmental and CivilEngineering， 2021，26（11）：5241-5258.

［16］ 王晓明，夏露，郑银河，等. 基于三维裂隙连通率的裂隙岩体表征单元体研究［J］. 岩石力学与工程学报，2013，32（S2）：3297-3302.

［17］ ZHOU C T， XU C S， KARAKUS M， et al. A systematicapproach to the calibration of micro-parameters for the flatjointedbonded particle model［J］. Geomechanics and Geoengineering，2018，16（5）：471-482.

（责任编辑：向飞）

基金项目：湖南省研究生创新项目（QL20220216）