基于名义粒径的砂岩颗粒破碎强度及颗粒集合抗剪强度的尺寸效应研究

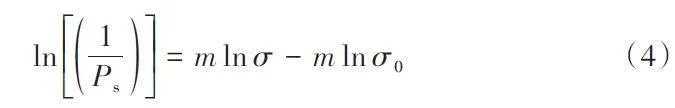
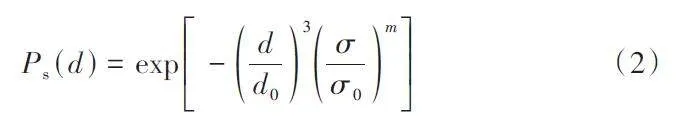
摘 要：对单颗粒和颗粒集合分别进行单轴压缩试验和直剪试验，探究不同尺寸、含石量和最大粒径下颗粒强度特征。基于Weibull统计模型建立颗粒强度尺寸效应公式，统计单颗粒名义粒径尺寸占比并推出级配曲线，再将名义粒径级配曲线与颗粒集合级配曲线对比，得到颗粒集合中特征粒径与名义粒径转化关系，由此得到从单颗粒推广到颗粒集合的强度尺寸效应公式，并检验公式适用性。结果表明：砂岩颗粒强度具有明显的尺寸效应；强度尺寸效应公式可以更好地预测天然级配堆石料的强度参数，对实际工程具有一定的指导意义。

关键词：单颗粒；破碎强度；粒径转化；颗粒集合；尺寸效应

中图分类号：TV641 文献标识码：A 文章编号：1001-9235（2024）09-0083-10

1 概述

在土石坝和路基等高填方工程中，颗粒的最大粒径可高达1 200 mm，但受限于当前的试验设备和条件，难以直接开展室内试验。为此，常规做法是对原料进行缩尺处理，进而研究缩尺试样的力学特性，并提取相关参数以模拟预测实际工程情况。经过缩尺后，最大粒径通常落在10～60 mm的范围内，缩尺比例高达20倍，这种差异相当显著。值得注意的是，缩尺后不同尺寸的颗粒在强度与变形特性上展现出显著差异，尤其是粒径较大的颗粒，其强度反而较低。因此，通过室内试验获得的结果具有显著的尺寸效应。

岩土颗粒材料的力学特性与普通岩土材料相比存在显著差异，其独特之处在于破碎特性及强度尺寸效应。多位学者对此进行了深入研究，迟世春等［1］通过单颗粒破碎试验，观察到单颗粒强度存在明显的尺寸效应，即随着粒径的增加，单颗粒强度呈下降趋势。孟敏强等［2］针对不同粒径的钙质砂进行类似试验，同样发现钙质砂的破碎强度随粒径增大而减小，体现了显著的尺寸效应。此外，Kuang等［3］运用离散元方法模拟单颗粒破碎试验，探讨了颗粒尺寸和配位数对破碎的影响，并提出一个经验公式来计算考虑尺寸效应的抗拉强度。这些研究均表明，颗粒尺寸在岩土颗粒材料的力学特性中扮演着重要角色。

关于颗粒集合料的尺寸效应，当前主流观点认为这是由于颗粒集合料内部普遍存在的缺陷所致，且这些缺陷的含量和尺寸会随着粒径的增大而增加［4］。为探究尺寸效应对土石混合体剪切性能的具体影响，Li等［5］开展了大型室内直剪试验，并结合离散元模拟进行分析。田鑫［6］则结合室内大型直剪试验与数值模拟，深入研究了考虑颗粒破碎情况下的土石混合体缩尺效应。谭彩等［7］利用相同试样尺寸的直剪仪，对不同最大粒径的无黏性粗粒土进行了直剪试验，结果表明：随着最大粒径的增大，剪切带宽度和强度均有所增强，呈现出明显的强度尺寸效应。这些研究为理解颗粒集合料的尺寸效应及其在工程中的应用提供了重要依据。

Huang等［8］利用RMT-150C岩石力学试验系统，对30种天然卵石进行了单粒破碎试验，以探究压缩条件下岩石颗粒的特征应力表现。该特征应力被定义为在压缩过程中岩石颗粒所展现出的特定应力状态，见式（1）：

σ = F／d2 （1）

文献［8］中d 取上下压板之间的距离，文献［9］中d 取上下加载点之间的距离，杨阳等［10］在研究单颗粒强度特征时d 取上下加载板之间的距离［9］，F 为荷载-位移曲线上的峰值荷载。

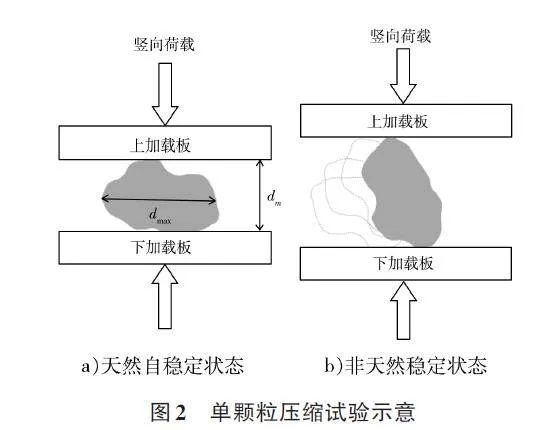
在进行单颗粒试验时，首先将颗粒平稳地放置在加载板上，确保其处于天然自稳定状态，见图1。当上下加载板与颗粒刚好接触时，停止加载，并利用式（1）计算得出单颗粒的强度特征值。然而，如果颗粒未能稳定地放置在加载板上，那么当颗粒接触到上下加载板时，它可能会发生旋转偏移。在这种情况下，当加载板与颗粒达到相对稳定状态时，所测得的峰值荷载往往与颗粒在天然稳定状态下测得的强度真实值存在偏差。因此，本文提出以下定义：颗粒在天然自稳定状态时，上下加载板之间的距离被定义为颗粒的名义粒径dm，在后续讨论中，将采用这个名义粒径dm来分析颗粒的强度。

许多研究通过室内试验，利用缩尺后的小尺寸试样来探究颗粒强度，并据此描述尺寸效应问题。深入理解尺寸效应对于准确预测颗粒原型尺寸的力学行为至关重要。因此，本文进行了室内单颗粒压缩试验和颗粒集合直剪试验，以研究粒径对单颗粒和颗粒集合强度尺寸效应的影响。在此基础上，提出了基于Weibull统计模型的单颗粒强度尺寸效应公式，并建立了单颗粒名义粒径与颗粒集合特征粒径之间的关系，从而推导出了颗粒集合的强度尺寸效应公式。还讨论了这些公式的适用性，并为预测原尺颗粒强度值提供了依据。

2 单颗粒强度尺寸效应方程

2. 1 单颗粒压缩试验及颗粒集合直剪试验

试验材料选用自施工现场获取的微风化砂岩料，其含水率控制在1. 2%。由于直接从现场取得的砂岩料粒径偏大，无法满足室内试验的规格要求，因此需对砂岩料进行二次破碎和筛分处理。在这一过程中，采用了颚式破碎机对试验材料进行破碎，以确保其粒径符合试验标准。

2. 1. 1 单颗粒压缩试验

试验装置选用长春机械研究所制造的DDL200型通用试验机。在进行单颗粒单轴压缩试验时，试验过程见图2。上下加载板之间的距离定义为名义粒径dm。

随机挑选了共计300个砂岩颗粒，分别属于10～20、>20～40、>40～60 mm3 个不同粒组，并对这些颗粒进行了单颗粒强度试验。整个试验过程严格遵循GB/T 50123—2019《土工试验方法标准》的规定。①首先，将颗粒平稳地放置在下加载板上，通过微调上下加载板之间的距离，确保它们刚好与颗粒接触。此时，测量并记录上、下加载板之间的距离，这被定义为颗粒的名义粒径dm。随后，以1 mm/min的加载速率开始试验。②在试验过程中，仪器会自动记录荷载与位移的变化数据。试验结束后，提取这些数据中的荷载-位移曲线峰值点值，即峰值荷载，这将用于后续颗粒强度的计算。

2. 1. 2 颗粒集合直剪试验

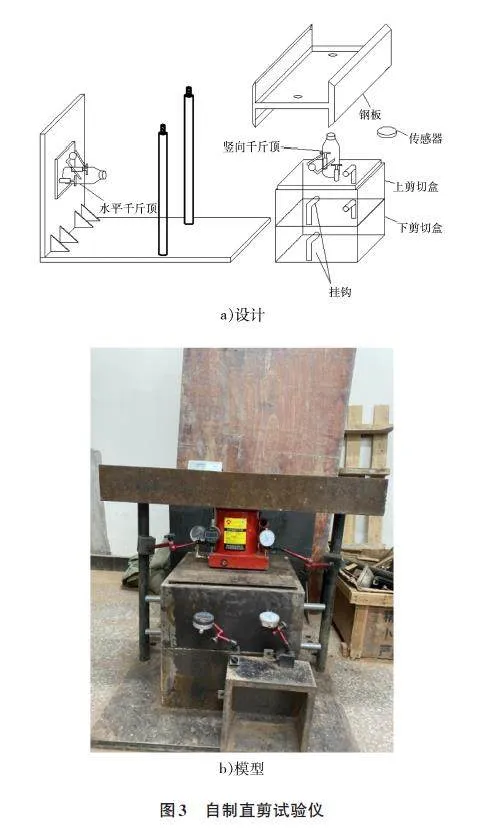
采用自制大型直剪仪对颗粒集合料进行室内直剪试验，见图3，试验仪器由几部分组成：剪切盒、千斤顶、位移计、反力装置、压力传感器、圆形钢条。

设计了7组室内直剪试验，旨在研究不同含石量和最大粒径对土石混合体剪切性能的影响。其中，含石量分别设定为40%、50%、60%、70%，并在含石量为70% 的条件下，设置最大粒径为10、20、40、60 mm的不同试验组。此外，每组试验均在100、200、300、400 kPa的法向压力下进行。①准备试验土料和砂岩颗粒料，按级配配置好分层装入直剪盒并击实；②对试样施加竖向荷载，当竖向压力达到需要的数值并保持稳定后，对上剪切盒施加水平力。记录试验数据，待水平剪切位移达到试样直径的1/10时剪切完成。

2. 2 基于Weibull统计的单颗粒强度尺寸效应公式

2. 2. 1 Weibull统计模型

研究表明，颗粒强度服从Weibull 分布，基于Weibull最弱环理论，对于在平板之间加载的直径为d 的颗粒，其生存概率见式（2）［11］：

式中：d0为颗粒的参考粒径，mm；σ0为颗粒在幸存概率为37%时对应的特征应力，MPa；m 为Weibull模量，随强度离散性的增加而减小，这种离散性决定了强度的尺寸效应。

某一粒组的颗粒累积幸存概率为式（3）［12］：

Ps = 1 - i／n + 1 （3）

式中：n 为试验压缩的颗粒总数；i 为颗粒强度按升序排列所对应的序列号。

对于相同粒径的颗粒，d=d0，代入式（2）并对公式两边取对数，得式（4）：

因此，颗粒强度与累计幸存概率之间存在线性关系，其中Weibull模量代表了直线的斜率，而特征应力则可以通过直线在x 轴上的截距计算得出。由于相同粒径的岩石颗粒在单粒强度上表现出一定的离散性，目前常采用特征应力来代表该粒径岩石颗粒的单粒强度特性［13］。

2. 2. 2 Weibull分布结果及分析

依据前述的Weibull统计模型，计算了砂岩颗粒的强度，并据此得到了颗粒的累计幸存概率。以颗粒所受强度的对数ln σ 作为横轴，颗粒未破碎概率的双对数ln［ln（Ps）］作为纵轴，绘制了砂岩颗粒在10～20、>20～40、>40～60 mm 3 个粒组下的强度Weibull分布（图4）。从图中可以观察到，除了低应力水平和高应力水平处的个别点外，砂岩颗粒的强度大体上符合Weibull分布规律。

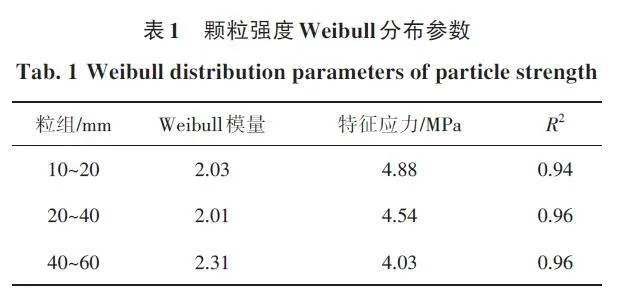
首先，根据图4中砂岩各粒组颗粒强度的拟合曲线以及式（4），计算得出了不同粒组单颗粒强度分布的Weibull参数。这些参数的具体数值已列于表1。从表1可以观察到，砂岩不同粒组的拟合线R2值为0. 94～0. 96，这表明拟合程度相当好。进一步分析发现，不同粒组的Weibull模量m 值处于一个相近的范围，具体为2. 01～2. 31，这表明模量m 与粒组之间并未呈现出明显的相关性。然而，特征应力则随着粒径的增大而减小，这一现象清晰地展示了尺寸效应的存在。

2. 2. 3 单颗粒强度尺寸效应方程

颗粒强度尺寸效应公式的建立一直是国内外学者在研究尺寸效应时关注的焦点。这一公式的建立对于预测无法通过仪器直接测量的大粒径颗粒强度具有重要意义，有助于突破实验室仪器尺寸对研究工作的限制。表2列出了目前常用的颗粒强度尺寸效应公式，这些公式为相关研究提供了重要的参考依据。

根据表2所示，McDowell等［14］提出的公式并未明确反映颗粒尺寸变化对强度的影响，Frossard等［4］和Ovalle等［16］的公式中均涉及了2种不同颗粒的强度与特征粒径之间的关系。邵晓泉等［17］提出的公式则明确描述了原尺颗粒与缩尺颗粒强度之间的关联，较好地体现了颗粒的强度尺寸效应。故本文运用此公式来拟合砂岩颗粒强度尺寸效应公式。在邵晓泉等［17］公式基础上对参数进行了改进，其中，B代表原尺寸大颗粒，S代表缩尺后小颗粒，d 取颗粒名义粒径平均值dmp，m 采用3个粒组Weibull模量平均值。

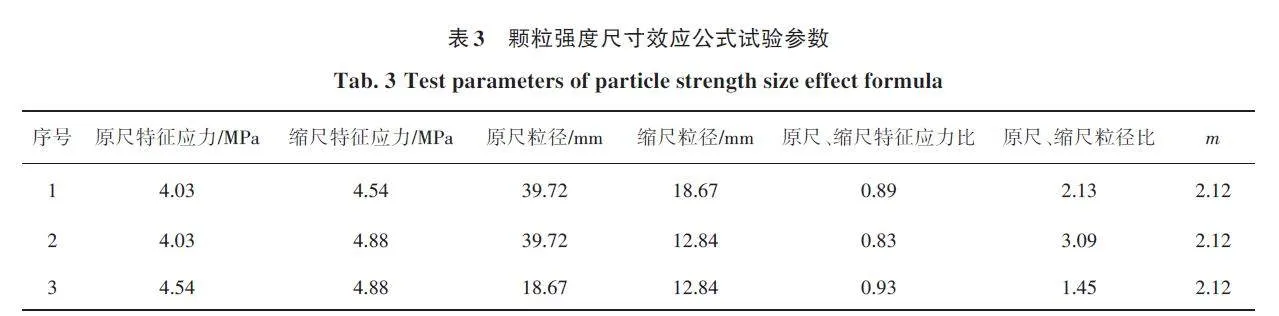
图4所示，通过描述原尺颗粒与缩尺颗粒的特征应力比和颗粒粒径比的关系，从而拟合参数nd，得到尺寸效应参数nd/m。表3 所示为砂岩颗粒基于Weibull统计模型的颗粒强度尺寸效应公式所需的试验参数。

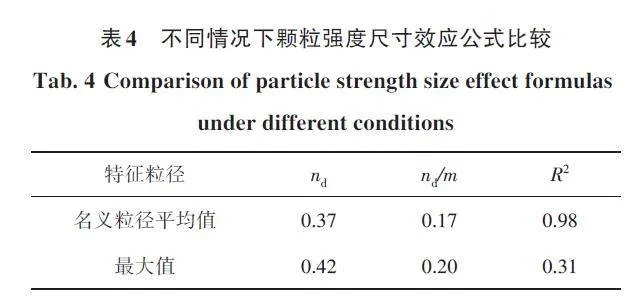
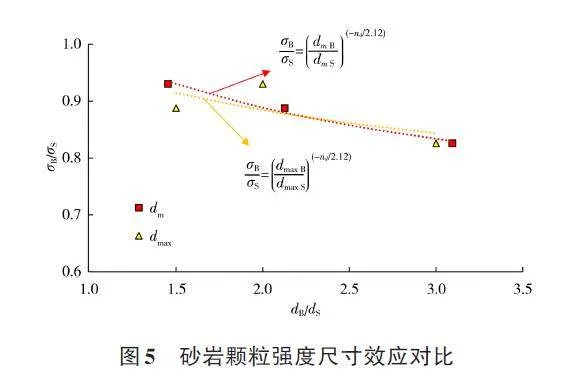
从图5中拟合得到单颗粒强度尺寸效应式（5），d 分别取名义粒径和最大粒径时的公式参数见表4：

从表4中的数据对比可以看出，当粒径取名义粒径平均值dmp时，砂岩尺寸效应公式的拟合效果更佳，其相关系数为0. 98，明显优于使用粒径dmax时的拟合效果。在整个粒组中，颗粒的粒径存在较大的差异，因此选取粒径的最大值并不能准确代表整个粒组的粒径特征，同时也会导致强度尺寸效应公式的拟合效果不佳。相比之下，选择dm作为代表粒径更为合适。此外，值得注意的是，公式中的nd 参数主要用于描述颗粒的外形形状。在对比2 种情况时，发现nd值仅相差0. 05，相差极小，对于公式计算结果影响不大，这是因为在讨论强度尺寸效应公式的时候只考虑了颗粒尺寸的影响，而进行试验的砂岩颗粒形状大多为棱角状，形状差异并不显著，故在2 种不同粒径情况下得到的形状参数nd 相差很小。

2. 3 各粒径组中名义粒径的颗粒含量分布曲线

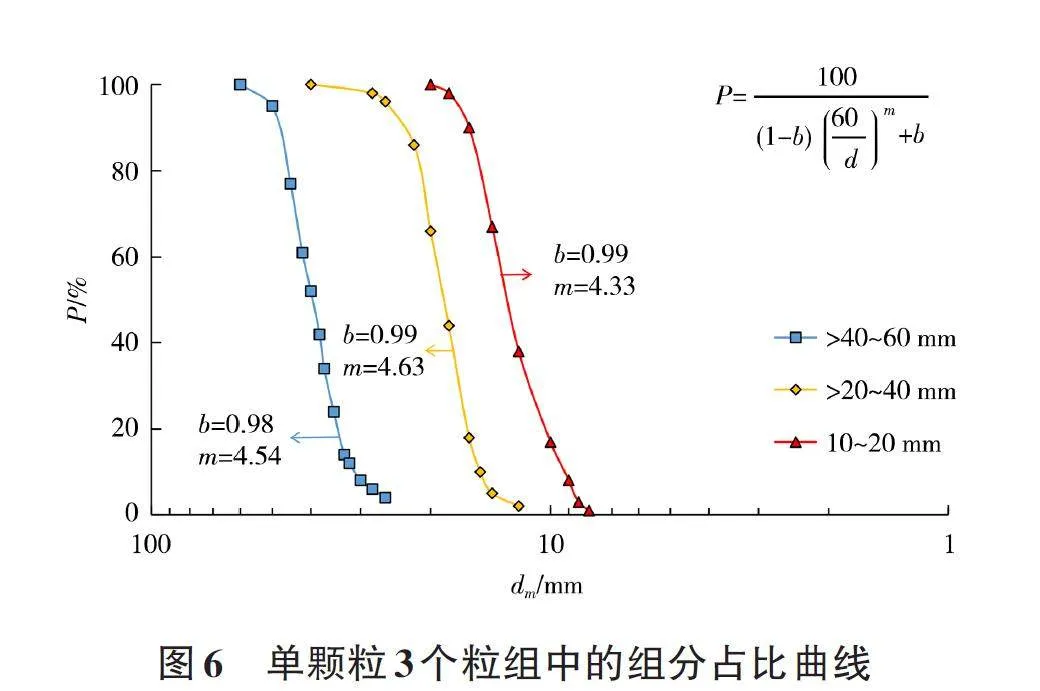
为了更深入地分析颗粒尺寸对强度的影响，对10～20、>20～40、>40～60 mm 这3 个粒组的共300 个颗粒的名义粒径进行了详细的统计分析。具体地将每个粒组进一步细分为更小的区间：60～>50、50～>45、45～>40、40～>35、35～>30、30～>20、20～>15、15～10 mm。随后，根据细分后各组分颗粒的数量比重，绘制了3个粒组中各组分的占比曲线，见图6。

从图中可以明显看出，每个粒径组中名义粒径颗粒数量的占比曲线形态表现出高度的一致性。具体来说，随着粒径的增加，颗粒数量呈现递减的趋势，并且在中间粒组范围内，这种递减的幅度尤为显著。为了更准确地描述这一趋势，采用了郭万里等［18］提出的级配方程式来进行量化分析。这一公式能够很好地拟合颗粒数量与粒径之间的关系，为后续的研究提供了有力的工具，见式（6）：

式中：P 为粒径小于d 的颗粒数量所占百分比，%；d为级配范围内任意粒径，mm；dmax为最大粒径，mm；b、m 为级配参数，通过拟合得到。

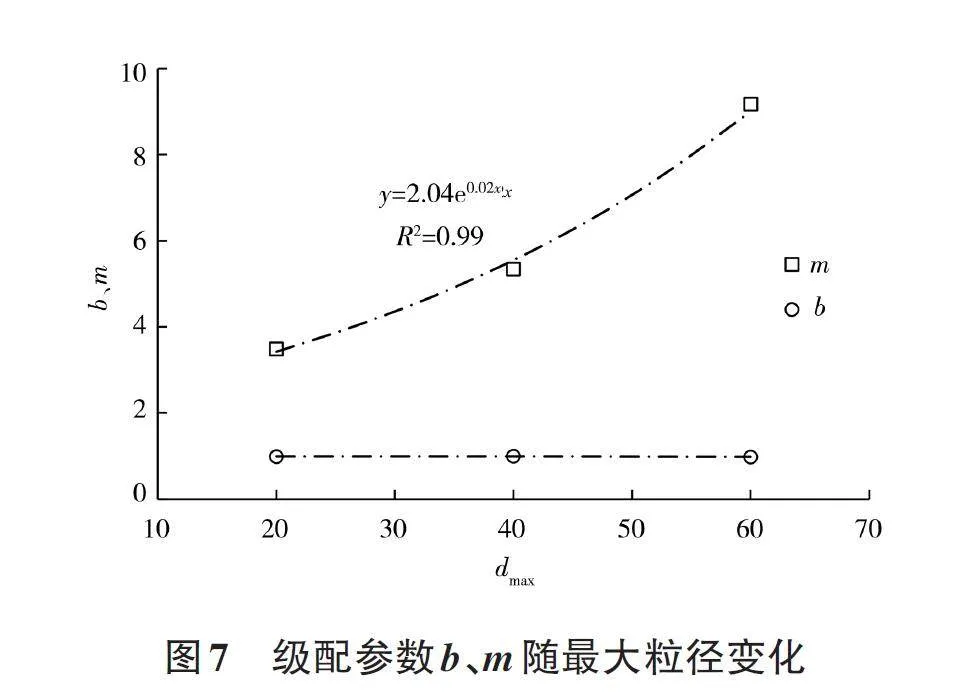
拟合名义粒径级配曲线得到参数b 和m，参数b和m 与最大粒径相关，见图7。可知，m 随着最大粒径的增大而呈指数型增大，b 随着最大粒径的增大而呈现不变的趋势。可采用式（7）进行描述：

m = 2.04e0.02dmax （7）

由于b 值随最大粒径的变化很小，故取平均值0. 99。然后将级配参数m 和b 代回到式（6），得到粒径组最大粒径表示的级配方程式（8）：

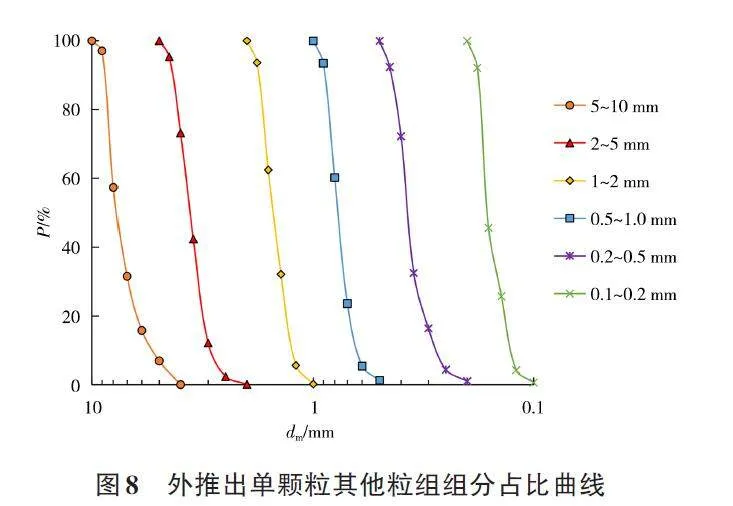
根据b、m 与粒组最大粒径的关系，可以得到粒组0. 1～0. 2、>0. 2～0. 5、>0. 5～1、>1～2、>2～5、>5～10mm的级配参数值，并外推出粒径在这些范围内的组分占比曲线，结果见图8。

从图8中可以观察到，通过外推得到的其他粒组的名义粒径级配曲线与图6中展示的曲线形态相似，不同粒组之间的变化趋势也大致相同。特别地，当P 值位于20%～80%时，曲线变化较为陡峭，呈现出近似直线的形态；而当P 值大于80% 或小于20%时，曲线的减小趋势则变得较为平缓。根据这一观察，可以利用式（8），并结合b、m 与粒组最大粒径之间的关系，推算出其他粒组的名义粒径级配曲线。这一方法提供了一种有效的工具，能够更系统地研究不同粒组的粒径分布特征。

2. 4 名义粒径与最大粒径的关系

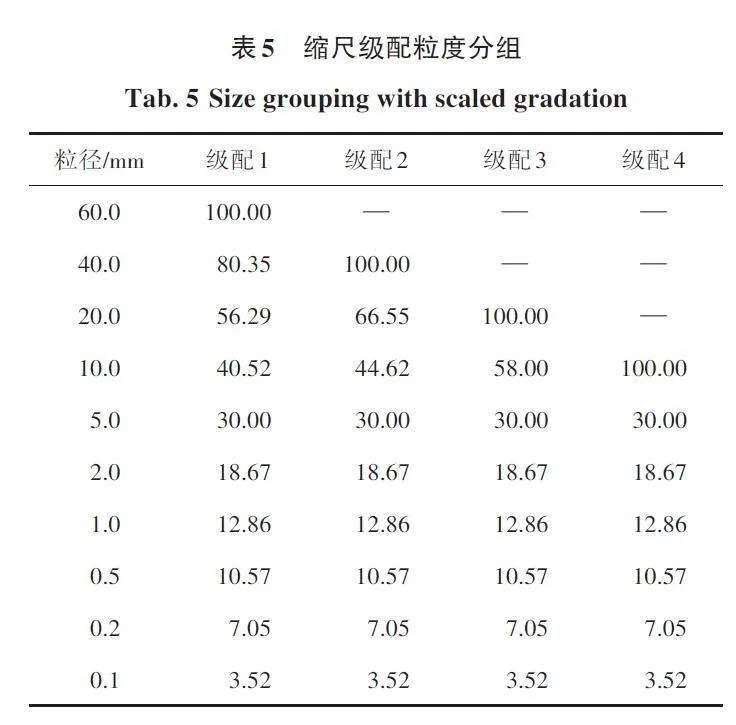
基于庙堂水库主堆石料的级配曲线，采用了等量替代法进行缩尺处理。通过应用式（9）进行计算，设计了4种不同的级配方案。这些方案旨在深入研究室内缩尺试样中最大粒径对颗粒集合料剪切特性的影响。级配设计细节和研究结果见表5。

Pi = （Poi／P5 - Pdmax）P5 （9）

式中：Pi为替代后某粒组含量，%；Poi为原级配某粒组含量，%；Pd max为超粒径颗粒含量，%；P5为粒径超过5 mm的颗粒含量，%。

颗粒级配曲线可采用单颗粒名义粒径颗粒含量级配曲线进行描述，将式（9）代入到庙堂水库的4种级配中，计算得到基于名义粒径的级配曲线，具体过程如下。

a）计算颗粒集合每种级配中各粒组的组分比重P。如级配1中粒组60～40的比重：P60～40=P60-P40=100%-80. 35%=19. 65%。

b）将图6中名义粒径各粒组含量值Pm与步骤1中相对应的粒组组分比重P 相乘，得到单颗粒名义粒径粒组在颗粒集合料中的完整占比Pw。Pw 60～40=Pm 60～40×P60～40。

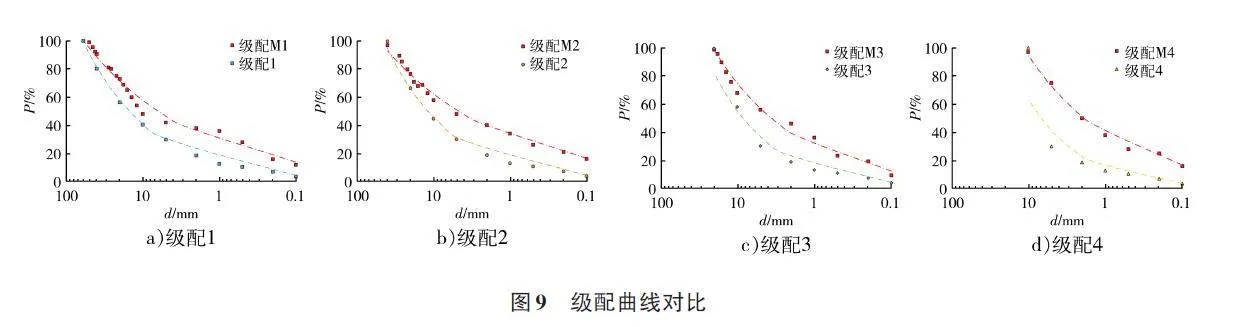
c）步骤2 计算得到的Pw60～40、Pw 40～20、Pw 20～10、Pw 10～5、Pw 5～2、Pw 2～1、Pw 1～0. 5、Pw 0. 5～0. 2、Pw 0. 2～0. 1就是基于名义粒径的完整级配，并将其与颗粒集合的4种级配进行对比，见图9。

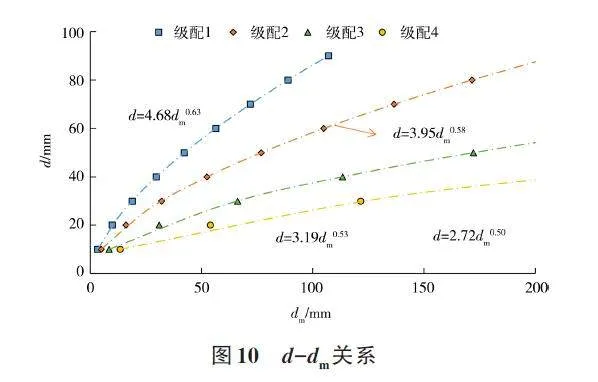
图9显示了基于名义粒径的级配曲线与最大粒径不同的4条级配曲线的对比。图9可知，不同最大粒径下的级配曲线与名义粒径级配曲线的变化趋势相同，但2条曲线之间存在差异，这个差异反映了最大粒径与名义粒径的关系。将级配曲线中按照小于某粒径组质量占比i 相同的粒径取值，得到粒径di-dmi值，并绘制图10，拟合d-dm关系式。

从图10中拟合得到d 和dm的关系，见式（10）：

d = adCm（10）

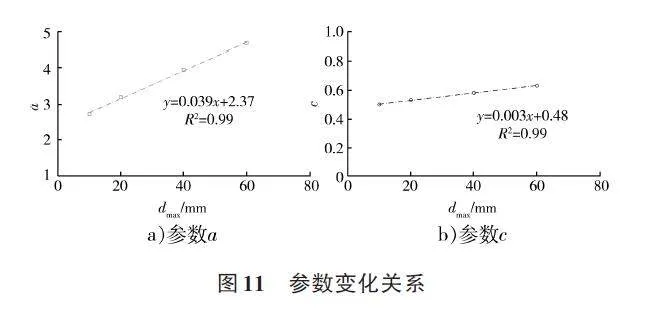
式中：d 为特征粒径；dm为名义粒径；a、c 为粒径转化参数。参数a 和c 与各粒径组最大粒径的关系可见图11，随着级配中最大粒径的增大，系数a 和指数c也随之增大，可见式（11）—（13）：

a = 0.039dmax + 2.37 （11）

c = 0.003dmax + 0.48 （12）

将式（11）、（12）代入到式（10），得到式（13）：

d = （0.039dmax + 2.37）dm（0.003dmax + 0.48） （13）

式中：d 为特征粒径；dm为名义粒径；dmax为粒组中的最大粒径。

上述公式为正常级配曲线中对应的特征粒径与名义粒径转化的公式，可见：d-dm 的关系式体现了单颗粒名义粒径dmi与颗粒集合特征粒径di的转化关系，对后续颗粒集合强度尺寸效应公式的推导建立联系。

3 名义粒径对抗剪强度影响的讨论

3. 1 名义粒径尺寸效应对抗剪强度包线的影响

Ovalle等［16］确立了颗粒破碎强度与粒径之间的关系，为了确保不同粒径的颗粒材料在受到剪切作用时能够呈现出相同的破碎率，对颗粒集合的抗剪强度按（d2 /d1 ）-nd/m因子进行折减，见式（14）：

τG2 = τG1（d2／d1 ）-nd/m（14）

根据式（14）来拟合颗粒集合尺寸效应公式，d为颗粒集合料的特征粒径，根据式（13），将其转化为名义粒径dm描述，见式（15）：

τB／τS = （dmB／dmS ）-nd/m（15）

式中：dm 为名义粒径；nd 为几何相似性参数；m 为Weibull模量；nd/m 为尺寸效应参数。其中B代表大颗粒，S代表小颗粒。

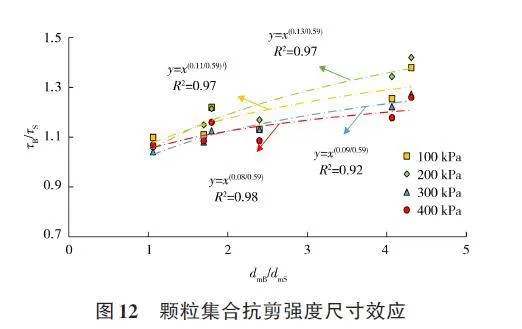
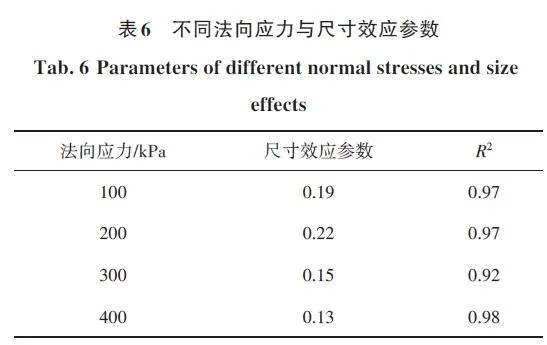
图12为不同法向应力下颗粒集合料的抗剪强度，拟合得到颗粒集合料的抗剪强度尺寸效应式（15），并将不同法向应力与尺寸效应参数值列在表6。

由表6可知，不同法向应力下颗粒集合料强度尺寸效应参数不同，随着法向应力增大，尺寸效应参数先增大后减小，在200 kPa时达到最大值。这是因为当法向应力继续增大到某一特定值时（本文中为200 kPa），材料可能达到了一个临界点。在这个点上，材料内部的应力分布和结构调整达到了一个平衡状态，使得尺寸效应的影响达到最大。超过这个临界点后，随着法向应力的进一步增大，材料可能开始发生破坏或塑性变形，这可能导致尺寸效应参数开始减小。

3. 2 基于名义粒径的强度尺寸效应公式适用性讨论

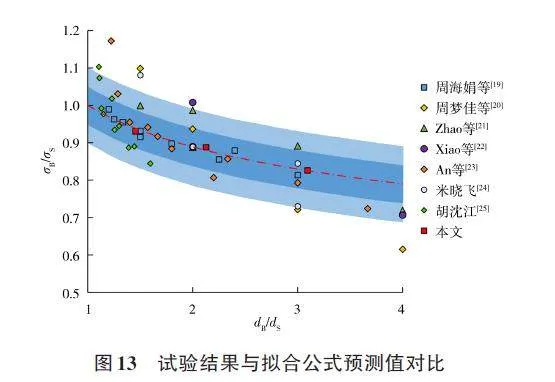
为了验证本文提出的强度尺寸效应式（5）的适用性，选取了其他学者［19-25］试验成果进行对比分析，见图13。

为了深入讨论颗粒强度的尺寸效应，许多学者进行了一系列试验。周海娟等［19］和周梦佳等［20］均采用数值模拟对大粒径堆石料颗粒进行试验，Zhao等［21］与本文用于试验的粒径相同分别为10、20、40、60 mm。Xiao等［22］对小粒径2. 5、5、10 mm的堆石材料进行了单粒破碎试验，An等［23］和胡沈江［25］均采用离散单元法研究堆石坝砂砾材料的尺寸效应，且粒径范围都在10～60 mm，米晓飞［24］对20～240 mm范围内的大连石灰石颗粒进行单颗粒强度室内试验。本文选取的这些学者试验粒径分布较广，试验方法和颗粒材料多样，能较好地进行讨论和预测。

由图13可以看出，试验实测值较为均匀地分布在本文的预测值线两侧，图中蓝色区域为预测值与试验实测值的误差带区域，深蓝色区域为5%的误差范围，浅蓝色区域为10% 的误差范围。结果显示，大部分数据点的误差范围为深蓝色区域，位于预测线前半段的数据点明显多于后半段数据点。公式拟合值与试验实测值相比具有较高的关联性，说明本文提出的拟合公式可以在无法测得现场大尺寸颗粒强度值时，通过室内小尺寸颗粒试验值计算得到，从而为堆石料的强度估算提供参考。

4 结论

a）强度尺寸效应公式中d 取名义粒径；单颗粒强度随名义粒径的增大而减小；颗粒集合料抗剪强度、粘聚力与内摩擦角随最大粒径的增大而增大，呈现出明显的尺寸效应。

b）堆石料颗粒试验值分布在本文强度公式预测线周围，吻合度高且变化趋势一致。故本文提出的强度尺寸效应公式能对堆石料颗粒的强度值提供参考。

参考文献：

［1］ 迟世春，王峰，贾宇峰，等. 考虑细观单粒强度的堆石料破碎特性研究［J］. 岩土工程学报，2015， 37（10）：1780-1785.

［2］ 孟敏强，袁正鑫，蒋翔. 钙质砂-石英砂单颗粒破碎-强度-尺寸效应试验研究［J］. 中国科学：技术科学， 2022，52（7）：1035-1047.

［3］ KUANG D M， LONG Z L， GUO R Q， et al. Numerical Investigation of the Cushion and Size Effects During Single-Particle Crushing via DEM［J］. Acta Mechanica Solida Sinica，2020，33（6）：851-863.

［4］ FROSSARD E， HU W， DANO C， et al. Rockfill shear strength evaluation： a rational method based on size effects ［J］.Géotechnique，2012，62（5）：415-427.

［5］ LI S Q， YANG Z P， TIAN X， et al. Influencing factors of scale effects in large-scale direct shear tests of soil-rock mixtures based on particle breakage［J］. Transportation Geotechnics，2021，31.DOI：10. 1016/j. trgeo. 2021. 100677.

［6］ 田鑫. 考虑颗粒破碎的土石混合体大型直剪试验缩尺效应研究［D］. 重庆：重庆大学，2020.

［7］ 谭彩，王琛，吴勇，等. 无黏性粗粒土直接剪切试验的强度尺寸效应［J］. 四川大学学报（工程科学版）， 2016，48（S1）：94-99.

［8］ HUANG Q S， ZHOU W， MA G， et al. Experimental and numerical investigation of Weibullian behavior of grain crushing strength［J］. Geoscience Frontiers，2020，11（2）：401-411.

［9］ HIRAMATSU Y，OKA Y. Determination of the tensile strength of rock by a compression test of an irregular test piece［J］.International Journal of Rock Mechanics and Mining Sciences &Geomechanics Abstracts，1966，3（2）：89-90.

［10］ 杨阳，张春会，崔恩杰，等. 单颗粒与单粒组钙质砂破碎特性及其关联关系研究［J］. 岩石力学与工程学报，2022，41（S2）：3410-3418.

［11］ MCDOWELL G R，AMON A. The Application of Weibull Statistics to the Fracture of Soil Particles ［J］. Soils and Foundations，2000，40（5）：133-141.

［12］ 李杨，佘成学. 堆石料单粒强度尺寸效应的颗粒流模拟方法研究［J］. 岩土力学，2018，39（8）：2951-2959，2976.

［13］ LIM W L， MCDOWELL G R，COLLOP A C. The application of Weibull statistics to the strength of railway ballast［J］. Granular Matter，2004，6（4）：229-237.

［14］ MCDOWELL G R，BOLTON M D. On the micromechanics of crushable aggregates［J］. Géotechnique，1998，48（5）：667-679.

［15］ NAKATA Y， HYDE A F L， HYODO M， et al. A probabilistic approach to sand particle crushing in the triaxial test［J］.Géotechnique，1999，49（5）：567-583.

［16］ OVALLE C， FROSSARD E， DANO C， et al. The effect of size on the strength of coarse rock aggregates and large rockfill samples through experimental data［J］. Acta Mechanica，2014，225（8）：2199-2216.

［17］ 邵晓泉，迟世春. 堆石料变形参数的粒径尺寸相关性研究［J］.岩土工程学报，2020，42（9）：1715-1722.

［18］ 郭万里，朱俊高，余挺，等. 土的连续级配方程在粗粒料中的应用［J］. 岩土力学，2018，39（10）：3661-3667.

［19］ 周海娟，马刚，袁葳，等. 堆石颗粒压缩破碎强度的尺寸效应［J］. 岩土力学，2017，38（8）：2425-2433.

［20］ 周梦佳，温彦锋，邓刚，等. 堆石料单颗粒劈裂试验破碎强度随机性与尺寸效应的三维离散元模拟［J］. 岩土力学，2019，40（S1）：503-510.

［21］ ZHAO X L， ZHU J G， JIA Y， et al. Experimental and numerical study of size effects on the crushing strength of rockfill particles ［J］. International Journal for Numerical and Analytical Methods in Geomechanics，2022，46（11）： 2060-2086.

［22］ XIAO Y， MENG M Q， DAOUADJI A， et al. Effects of particle size on crushing and deformation behaviors of rockfill materials ［J］. Geoscience Frontiers，2020，11（2）：375-388.

［23］ AN N， MA G， ZHOU H， et al. DEM investigation of the microscopic mechanism of scale effect of sandy gravel material［J］. Acta Geotechnica，2022，18（3）：1373-1390.

［24］ 米晓飞. 堆石颗粒强度的尺寸效应研究［D］. 大连：大连理工大学，2019.

［25］ 胡沈江. 堆石料颗粒破碎强度隐式离散元法研究［D］. 杭州：浙江大学，2022.

（责任编辑：程茜）

基金项目：重庆博士后科学基金资助项目（228512）