探矛盾之“因” 还运动之“本”

摘 要：以电磁感应知识为背景的“双杆问题”通常涉及导体杆做较为复杂的变加速运动，需运用微元法来处理问题。然而，试题中时间的赋值需要命题者严格求解和验证，才能避免导体杆运动速度或位移不自洽的矛盾。以一道高三质检压轴题为例，深入探讨引起矛盾的原因，还原双导体杆在磁场中运动的本来面目。

关键词：电磁感应；双杆问题；变加速；数据自洽

中图分类号：G633.7 文献标识码：A 文章编号：1003-6148（2024）10-0073-4

收稿日期：2024-06-01

基金项目：福建省教育科学“十四五”规划2023年度“协同创新”专项课题“指向物理观念形成的高中物理大概念教学实践研究”（Fjxczx23-371）；福建省教育科学“十四五”规划2023年度课题“基于科学思维的高中物理模型建构能力培养的课堂实践”（FJJKZX23-100）。

作者简介：颜辉（1986-），男，中学高级教师，主要从事中学物理教学工作和命题解题研究。

双导体杆在匀强磁场中做切割磁感线运动，因两根杆的相对速度不断改变，而使得导体杆中的感应电流和安培力不断变化，故“双杆问题”是典型的变加速模型问题。对变加速模型问题，设置数据时，由于所用知识超出高中物理范畴，或命制试题时随意杜撰数据导致数据不自洽，影响了试题的科学性［1］。近期某市高三质检压轴题考查匀强磁场中双导体杆的运动问题，试题中两个“时间”引起很多师生的质疑和讨论，以下深入探讨引起矛盾的原因，还原双导体杆的真实运动规律。

1 引起质疑和讨论的两个“时间”

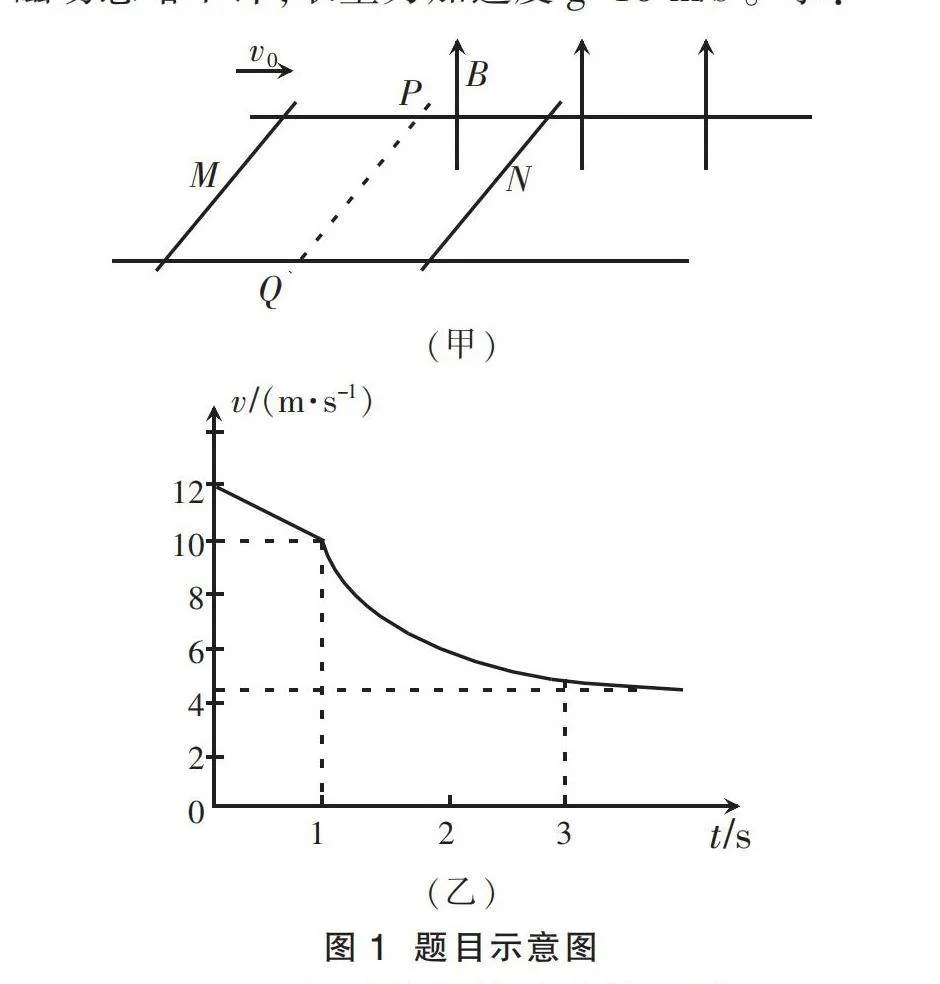
如图1（甲）所示，两平行长直金属导轨水平放置，间距L=0.8 m。PQ右侧区域有匀强磁场，磁感应强度大小B=0.5 T，方向竖直向上。t=0时，磁场外的细金属杆M以v0=12 m/s的速度向右运动。t=1 s时，细金属杆M恰好到达PQ处。同时，对磁场内处于静止状态的细金属杆N施加一与轨道平行的水平恒力，其大小F=0.8 N。N杆运动2 s后两杆速度相等，两金属杆与导轨接触良好且运动过程中始终与导轨垂直，细金属杆M速度随时间变化的v-t图像如图1（乙）所示。两杆质量均为m=0.2 kg，与导轨间的动摩擦因数相同，在导轨间的电阻均为R=0.2 Ω，感应电流产生的磁场忽略不计，取重力加速度g=10 m/s2。求：

（1）金属杆与导轨间的动摩擦因数μ；

（2）为保证两杆不发生碰撞，初始时金属杆N到边界PQ的最小距离Δx；

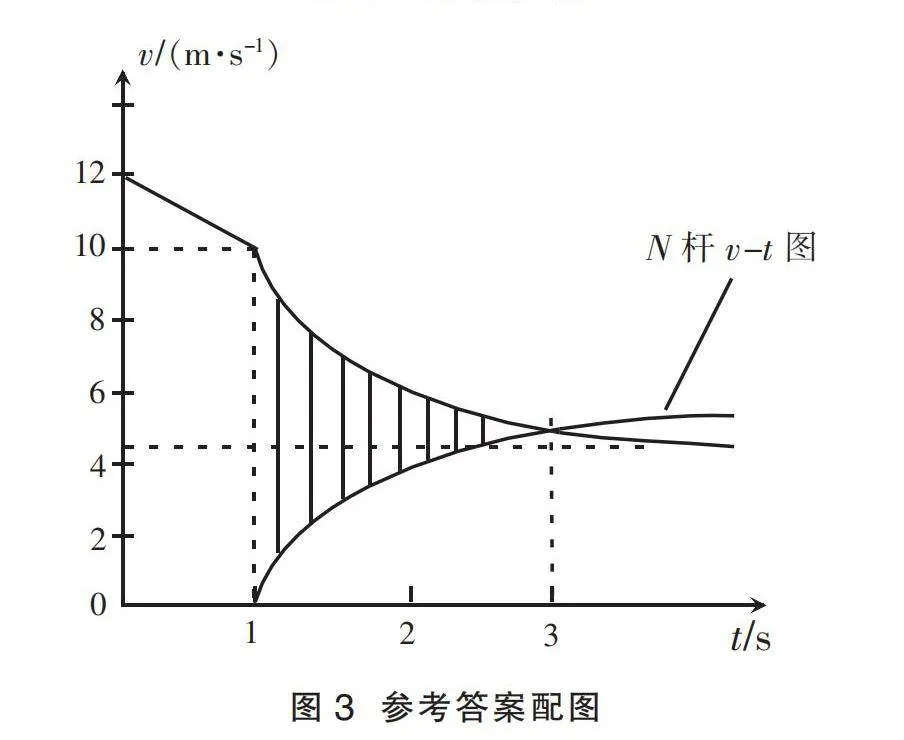
（3）金属杆N最终运动的速度大小vt，并作出金属杆N的速度随时间变化的v-t图像（无需过程说明）；

（4）若从金属杆N开始运动达到稳定运动状态经历Δt时间（Δt已知），求整个过程两根金属杆产生的总焦耳热Q。

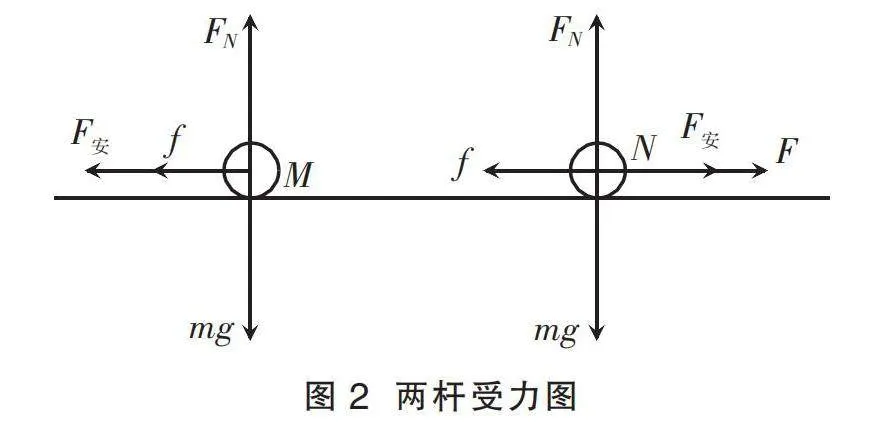
时间1 “N杆运动2 s后两杆速度相等”。M杆进入磁场后，N杆也随之开始运动，两根杆的受力情况如图2所示，对M、N杆组成的系统进行受力分析有F=2μmg，因此，满足动量守恒mv1=2mv，得v=5 m/s。对N杆运用动量定理

Ft+BILt-μmgt=mv-0

其中，BILt==

代入过程经历的时间2 s，易得两根杆共速前1～3 s内的相对位移Δx=xM-xN=0.5 m。再运用图像法进一步分析，因为M、N杆的质量相等，且分析发现它们所受合力总是大小相等、方向相反，所以N杆的运动和M杆的运动是对称的关系，两根杆均做加速度减小的变速直线运动。在第（3）问中画出N杆的v-t图像如图3所示，其中阴影部分的面积即为两根杆的相对位移，而该面积明显大于0.5 m。两种方法得出的结论出现了矛盾，究竟是哪里出了问题？

时间2 “从金属杆N开始运动达到稳定运动状态经历Δt时间”。M、N杆共速后，N杆的速度反超M杆，回路中的电流反向，各自受到的安培力也随之反向，最终两根杆会以不同的速度做匀速直线运动。然而，试题中并未给出一个具体的时间，而用Δt表示，难道双导体杆达到稳定状态的时间真的无法确定吗？

2 探讨矛盾之“因”

电磁感应中的“双杆问题”涉及两导体杆做变加速运动，变加速阶段的位移、速度和时间受特定条件制约，三个数据总是一一对应，它们的变化遵循一定的运动规律［2］。然而，时间赋值错误引起不自洽矛盾的根本原因是，在高中物理知识范畴里解决“双杆问题”时，将安培力的冲量表示为I=Ft=（vM-vN）t=，对导体杆运用动量定理I=Δp，合外力的冲量使得导体杆的动量发生变化。虽然初末状态是正确的，但是如果题干中的时间赋值出错，就会导致其他力（摩擦力、拉力等）的冲量出错，最终通过运算会得到一个错误的安培力冲量，从而引起不自洽的矛盾。要解决这一问题需要将两根杆的速度随时间的变化关系细致地刻画出来。

3 还原运动之“本”

3.1 两导体杆的真实运动规律

研究M杆进入磁场后两根杆的运动规律，两杆共速前vM>vN，俯视导轨中的回路有逆时针方向的电流，I=，F=（vM-vN）=

0.4（vM-vN）。两杆的受力情况如图2所示，取向右为正，根据牛顿第二定律，对M杆分析有

F+f=-mM（1）

代入题给数据得

0.4（vM-vN）+0.4=-0.2（2）

两杆构成的系统所受合外力为0，由动量守恒mM v1=mM vM+mN vN得

10=v+v（3）

由（2）（3）式整理得

4v-18=-（4）

分离变量得

-4dt=（5）

不定积分得

v=（4.5+Ce-4t） m/s（6）

将M杆刚进入磁场的速度v

=10 m/s代入（5）式得C=5.5。（7）

结合（3）（6）（7）式可得两杆的速度随时间变化的函数关系为

vM=（4.5+5.5e-4t） m/s（8）

vN=（5.5-5.5e-4t） m/s（9）

共速时，由动量守恒mv1=（m+m）v得v=

5 m/s，代入（8）式解得t= s≈0.599 s。因此，M杆进入磁场后经历约0.6 s，两杆就共速了，而不是题给的2 s。将正确的时间0.6 s代入计算M杆进入磁场后到两根杆共速的过程，两杆的相对位移为Δx=vdt-vdt≈1.90 m≠0.5 m。

由（8）（9）式可知，当t→∞时，5.5e-4t无限接近0，M杆的速度无限趋近v=4.5 m/s，N杆的速度无限趋近v=5.5 m/s。运用数学函数绘图工具“几何画板”可绘制M杆进入磁场后两根杆的速度v和v随时间变化的图像（图4）。将题干中t=2 s代入得v≈4.502 m/s，v≈5.498 m/s，显然两根杆在2 s时并非是共速，而已经是接近稳定的状态了。

接下来，笔者用微积分的方法进一步用两根杆达到稳定状态的过程中回路中产生的焦耳热进行验证。从N杆开始运动，到最终两杆达到稳定状态的过程中，回路中的电流大小为

整个回路中的热功率为

P=2I2R=（121e-8t-22e-4t+1）×0.4（11）

整个回路的电热为

Q=Pdt=［6.05×（1-e-8t）-2.2×（1-e-4t）+0.4t］ J（12）

两杆达到稳定的时间趋于无穷，得Q=（0.4Δt+3.85） J，求解结果与第（4）问的参考答案用系统动能定理所得结论是吻合的。从上面的理论分析我们发现，两根杆到达稳定状态的时间是趋于无穷的，而非一个确定的时间。

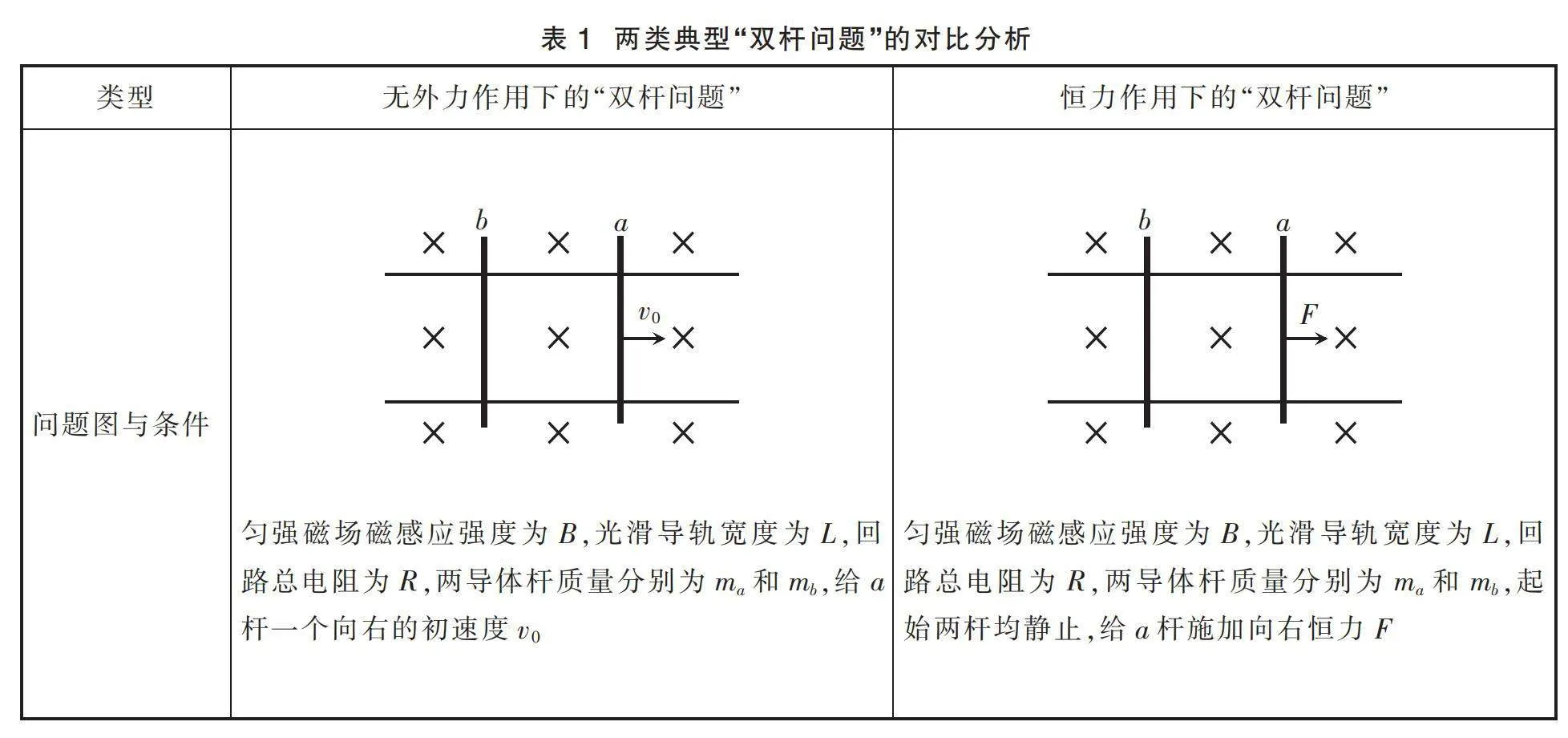
3.2 拓展两类典型的“双杆问题”

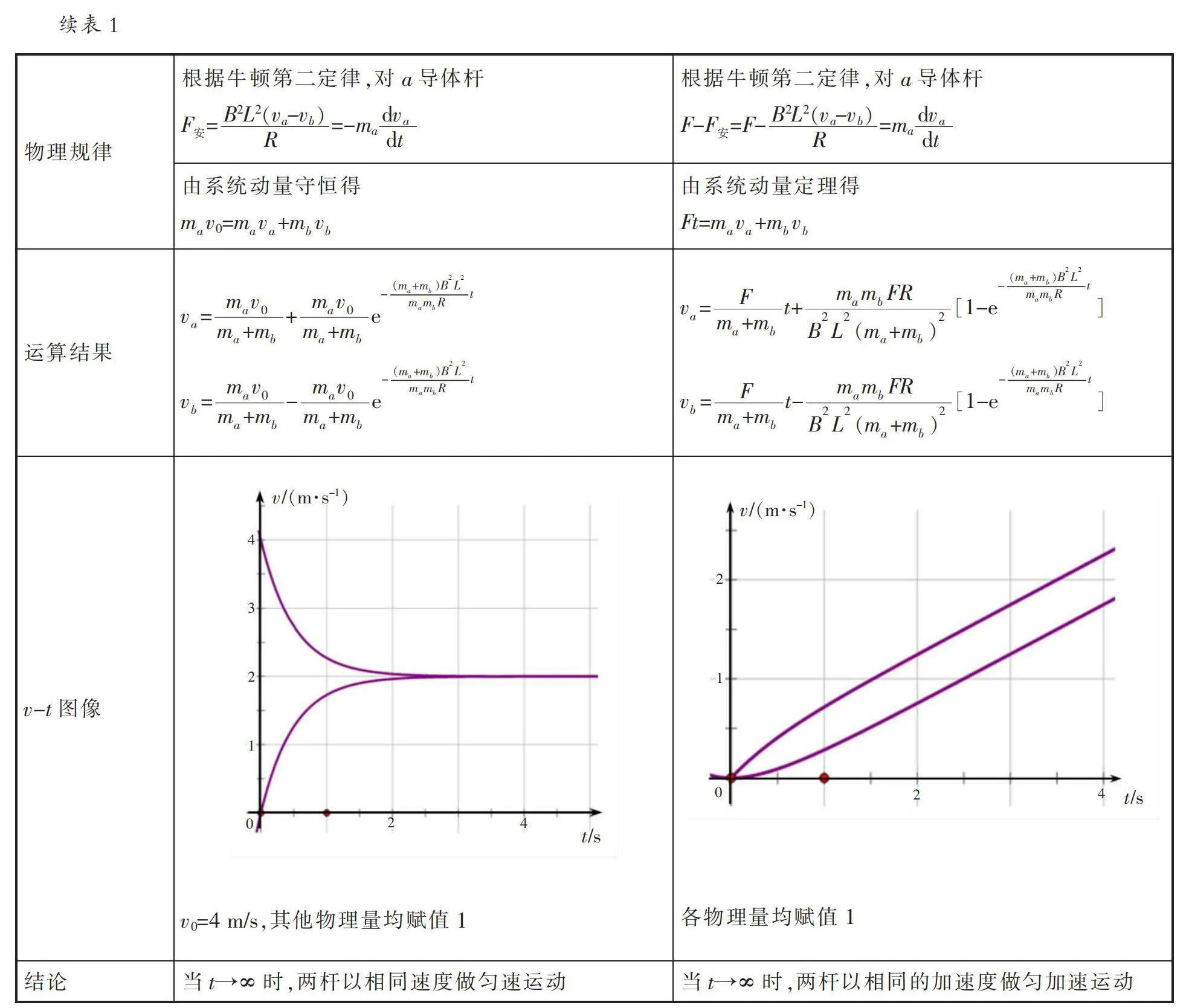
高中物理还有两类较典型的“双杆问题”，两导体杆构成的系统除了受到安培力外，一类是无外力作用，还有一类是有恒定外力作用，表1为这两类“双杆问题”的对比和分析。

4 小结与启示

通过以上三类高中物理常见的“双杆问题”的对比和分析后发现，导体杆的速度随时间的变化均是含有以自然常数e为底的指数函数关系。理论上，当时间t→∞时，两杆的运动状态才趋于稳定，而如果各个物理量给定了具体的数值，则可认为某时刻起双杆的运动状态近似达到稳定。因此，教师在命制电磁感应双杆切割的相关试题时，给出的具体数据应遵循科学性原则，逻辑自洽、结构严谨的试题可以培养学生正确的物理观念、科学思维和科学态度［3］。

物理教学需要培养学生敢于质疑和创新的思维品质。无论是新课教学还是复习备考，教师要有意识地创设质疑环境，主动提出引发疑问的思维问题［4］，而试题中的赋值错误则是培养学生质疑和创新的很好的教学资源。教师要善于捕捉学生质疑的火花，引导学生在遇到现阶段暂时无法解决的问题时，勇于突破学科和知识的边界，大胆进行跨学科实践和探索，在解决质疑问题的过程中提升自己的高阶思维和创新能力。

参考文献：

［1］王怀宾.“变加速模型”试题命制探讨［J］.物理教师， 2022，43（1）：64-66.

［2］李万杰.深度学习视域下一道电磁感应试题的探讨［J］.物理教学，2022，44（12）：53-56.

［3］华星亮，曾长兴.从“相对误差”谈收尾速度的合理性设问——以导体棒平动切割磁感线为例［J］.物理教学探讨，2023，41（7）：56-58，62.

［4］武长青.基于质疑创新的五个水平谈科学思维的培养策略［J］.物理教学，2020，42（4）：7-11.

（栏目编辑 蒋小平）