杉阔混交林自疏边界线研究

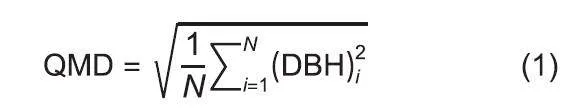
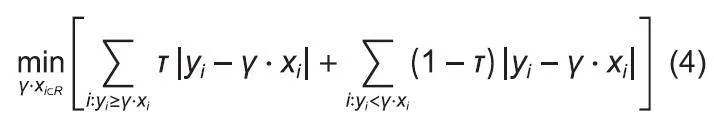
摘要：[目的]正确揭示混交林自然稀疏机制，是实现森林可持续经营目标的基础。[方法]本研究利用1991～2016年福建、江西和安徽省森林资源连续清查数据，采用线性回归分析、随机边界分析和分位数回归分析，研究树种混交、纬度变化和立地条件对杉阔混交林密度和生长之间自疏轨迹的影响规律。[结果]相较于杉木纯林，杉阔混交林自疏线呈上移且趋于平缓的状态。不管采用何种拟合方式，杉阔混交林自疏线与纯林自疏线变化规律基本一致，未偏离-1.605。混交比例对杉阔混交林自疏斜率具有正向影响，纬度和立地条件具有负向影响。线性回归模型拟合得到的是混交林的林分平均密度，分位数回归拟合得到的最大林分密度线受分位数值的影响，随机边界分析可以避免主观选择自疏拟合数据的缺陷，是混交林最大密度线的最佳拟合方法。[结论]杉阔混交林自疏轨迹与杉木纯林相一致，主要受混交比例、纬度和立地条件的影响，采用随机边界分析方法可以得到混交林最大林分密度，本研究可为杉阔混交林密度确定和调控提供实践指导。

关键词：杉阔混交林；林分自疏；树种混交；纬度；立地条件

中图分类号：S750 文献标识码：A 文章编号：1001-1498（2024）05-0001-12

在林分生长发育进程中，如果可利用生境资源和生长空间无法满足相邻树木间的需求，就会发生非对称竞争，出现随林分密度下降，林分生长量持续增加的情况。在双对数坐标中，林分密度和林分生长的数量关系接近直线，即林分自疏线。该自疏线是林地所能承载的林分密度理论上限。

纯林自疏线的斜率和截距是否发生变化，一直是自疏法则的研究重点。有研究表明：即使在树种、林龄、林分密度和立地条件等方面有所不同，林分自疏斜率和截距均不会发生变化。但也有学者指出，树种、立地质量、气候等因素，都会对自疏斜率和截距产生影响。另外，即使同一林分的自疏轨迹，也会因拟合方法的不同其斜率和截距也会有所差异。

在相同生境条件下，若混交林内树种之间具有良好的互补性，能充分利用生境资源和生长空间，林分密度会更大。例如，处于混交林下层的欧洲山毛榉（Fagus sylvatica L．）可明显提升林地土壤氮素含量，从而促进与其混交的欧洲赤松（PinussylvestrisL．）幼苗天然更新，其混交林密度要高于欧洲山毛榉和欧洲赤松纯林的密度。对南欧432个长期混交实验林进行研究发现，随气候和立地条件的梯度变化，混交林的林分密度比各混交树种纯林的林分密度平均值高16.5%，自疏线也明显偏离-1.605。因此，研究树种混交、立地条件和气候等因素对混交林林分密度和生长关系的影响规律，对于科学确定混交林最适调控密度具有重要的理论指导意义。

杉木（Cunninghamia lanceolata （Lamb.）Hook.）是国南方地区重要的用材树种，林分面积和木材蓄积均占第一。随着社会经济发展，人们对森林的需求不再仅限于木材，还包括森林生态系统的多功能性。目前，在浙江、安徽、江西、湖南、福建等杉木栽培区，主要采用“间伐杉木，补植阔叶树”的模式，对杉木纯林进行多功能改造。但这种改造模式在培育周期、林分密度、立地选择等方面缺乏明确理论依据，尤其是混交林密度调控，是影响杉阔混交林多功能的重要因素。本研究利用福建、江西和安徽的森林资源清查数据，以天然更新形成的杉阔混交林为研究对象，通过量化林分密度与生长之间的关系，探讨影响自疏轨迹的因素，以期为杉阔多功能混交林改建过程中确定最适林分密度提供理论依据。

1 研究方法

1.1 数据来源和样地分布

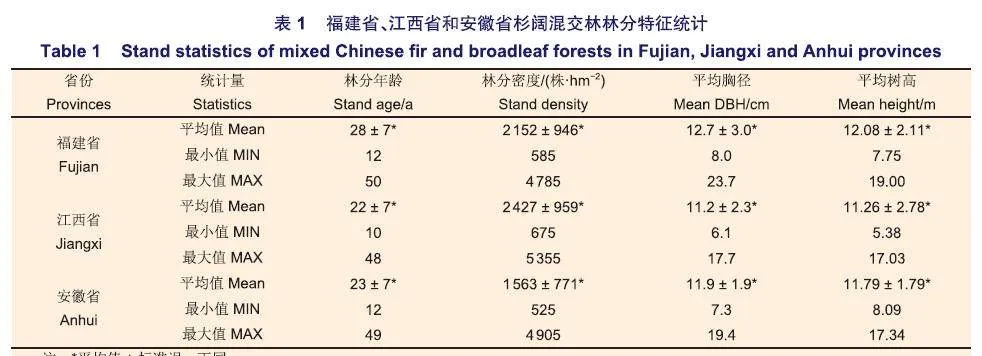
本研究数据来源于福建、江西和安徽3个省份的国家森林资源清查数据（1991～2016年）（图1）。福建省属亚热带季风气候，主要地貌为山地和丘陵，杉阔混交林内树种主要为：杉木、枫香（Liquidambar formosana Hance）、花榈木（Ormosia henryi Prain）、尖叶栎（Quercusoxyphylla （E.H.Wilson） Hand.-Mazz.）、木荷（Schima superba Gardner&Champ.）；江西省属亚热带季风气候，地形以低山和丘陵为主，混交林内树种主要为：杉木、檫木（Sassafrastzumu （Hemsl.） Hemsl.）、枫香、木荷、拟赤杨（Alniphyllum fortunei （Hemsl．）Penk.）；安徽省处于暖温带与亚热带的过渡地区，地形以平原、丘陵和山地为主，混交林内树种主要为：杉木、檫木、枫香、苦槠（Castanopsis sclerophylla（Lindl.） Schottky）。

上述3个省份清查样地选择标准如下：（1）杉木实生苗造林；（2）阔叶树为天然更新；（3）杉木蓄积量占林分总蓄积量的35%一65%（4）样地内杉木活立木株数逐步降低，而林分平均胸径逐步增加；（5）样地未发生风灾、雪灾和病虫害等环境干扰和人为破坏。基于以上标准，可确保所选样地林分处于自疏状态。适合本研究样地共计474块，其中，福建、江西和安徽省分别为149、146和179块样地，具体样地点分布见图1，林分特征见表1。

1.2 测量与计算

国家森林资源连续清查样地间隔和面积：福建省为4 km × 6 km，面积为0.0667 hm2；江西省4 km × 4 km，面积为0.08 hm2；安徽省为4 km ×3 km，面积为0.0667 hm2。每隔5年对样地内胸径大于5 cm的林木进行复测，具体包括：树种名称、胸径/cm、树高/m和树木状态（活／死）。同时记录样地的地理坐标（经纬度）、土壤因子（土壤类型、土壤厚度、土壤质地和腐殖质厚度）和地形因子（海拔、坡向、坡位和坡度）。

采用每公顷活立木株数，作为衡量杉阔混交林密度指标。

采用林分平均胸径（QMD），作为反映杉阔混交林生长指标，表达式如下：

式（1）中，（DBH）i表示样地内第i株活立木胸径，N表示样地内活立木数量。

通过计算杉木相对断面积与阔叶树相对断面积的比值（（BAChinesefir/BAtota）/（1 - BAChinesefir/BAtotal）），来表示杉阔混交林的混交比例。

纬度用来表示不同省份降水和温度等气候变化情况，用以分析气候条件对杉阔混交林林分密度—生长关系的影响。

以基准林龄20 a时，样地内最高的5%优势木的平均高度，估算每块样地的立地指数，以此表示样地的立地质量。

1.3 拟合方法

采用线性回归、随机边界和分位数回归模型3种方法，对杉阔混交林林分密度—生长关系进行拟合，确定林分自疏轨迹。

（1）线性回归

线性回归的形式为：

Yi=α+β·xi+εi（2）

式（2）中，yi为样地内活立木数量的测量值，xi为影响样地内活立木数量的自变量；α、r为模型参数；εi误差项。考虑到模型存在异方差问题，在进行参数估计时，通过赋予各个残差的平方不同的权重后求和，使加权之后的残差平方和最小。

（2）随机边界分析

随机边界分析考虑生境随机因素的影响，模型形式为：

lnyi=α+β·lnxi+εf=α+β·lnxi+υi- μi（3）

式（3）中：yi为样地内活立木数量的测量值；xi为影响样地内活立木数量的自变量；α为截距参数；β为向量参数；εi是复合误差项，μi代表林分生长空间占有程度，υi代表影响林分活立木数量的其他外界随机因素。

（3）分位数回归

分位数回归可以研究多个分位点上的回归关系，对异常值、因变量正态性或异方差问题有着很强的稳健性。其基本原理是利用因变量的条件分位数来建模，并通过最小化加权的残差绝对值之和来估计回归参数，即：

式（4）中：yi为因变量向量；xi为自变量向量；T为待估分位数值；γ为系数向量。采用分位数回归拟合林分自疏线的关键在于确定合适的分位数T，其拟合系数γ会因分位数T的不同而有所差异。本研究分别选取分位值T为0.90、0.95、0.99、0.995和0.999，对杉阔混交林自疏线进行拟合。

本研究以林分密度为因变量，林分平均胸径为自变量构建混交林林分自疏基础模型（模型1），逐步添加混交比例（01）（模型2）、纬度（D2）（模型3）和立地条件（D3）（模型4）等自变量，其中，D1={1。混交比例 0，其他 D2={1，维度 0，其他 D3={1，立地条件 0，其他，分别采用线性回归、随机边界分析和分位数回归拟合混交林林分自疏变量之间的关系，旨在分析树种混交、气候条件和立地条件对杉阔混交林最适林分密度的影响规律。

利用R软件绘制林分密度-林分平均胸径关系图；采用R软件的“Im”包和“quantreg”包进行最小二乘法和分位数回归拟合，随机边界分析采用FRONTER 4.1软件进行拟合。

2 结果

2.1 杉阔混交林林分自疏线变化

（1）线性回归

福建、江西和安徽3省的杉阔混交林林分密度与平均胸径间的斜率值均为负值，即随着自疏林分的生长发育，林分密度会相应降低（表2）。上述各省杉阔混交林的自疏斜率值，均大于纯林理论值-1.605，杉阔混交林自疏轨迹趋于平缓。但各省杉阔混交秫自疏斜率值的置信区间均包含-1.605，并未偏离林分自疏理论值。

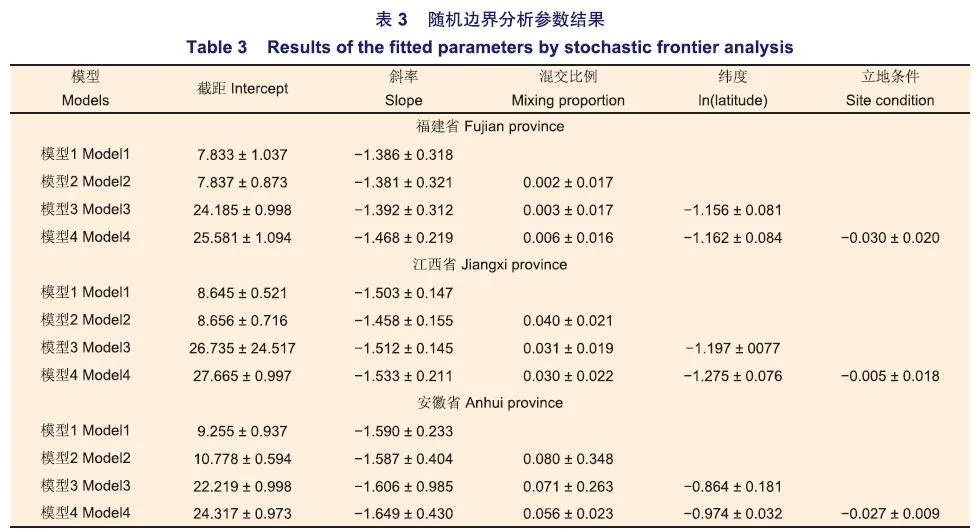
（2）随机边界分析

采用随机边界分析拟合基础模型中的林分密度与林分平均胸径间的数量关系发现，林分密度与林分平均胸径的自疏斜率值为负值，并未偏离-1.605，与最小二乘法拟合结果基本一致（表3）。但随机边界分析的自疏斜率值小于利用加权最小二乘法估计的斜率值。

（3）分位数回归

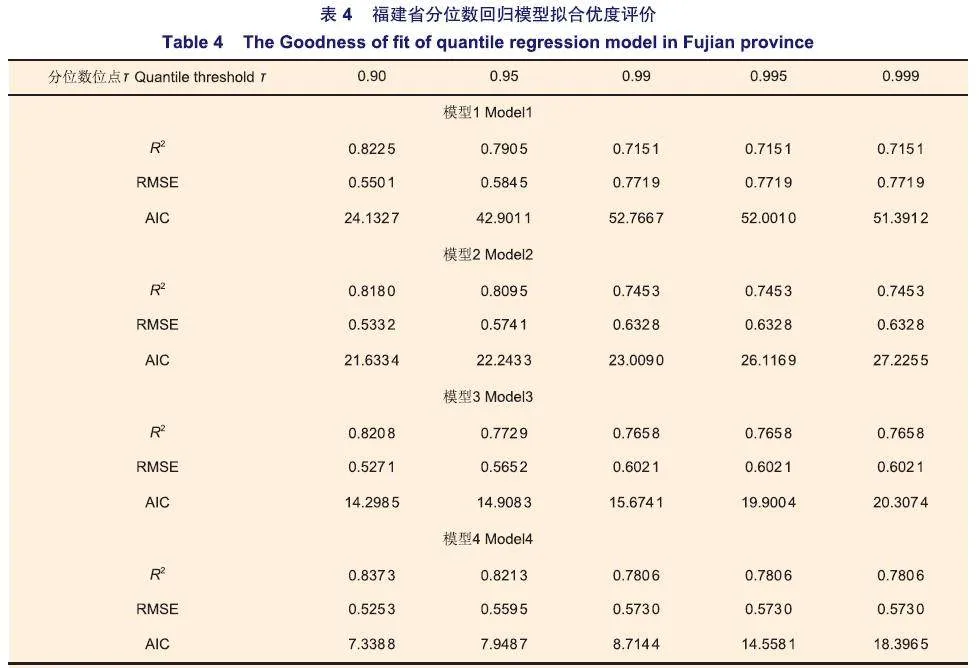
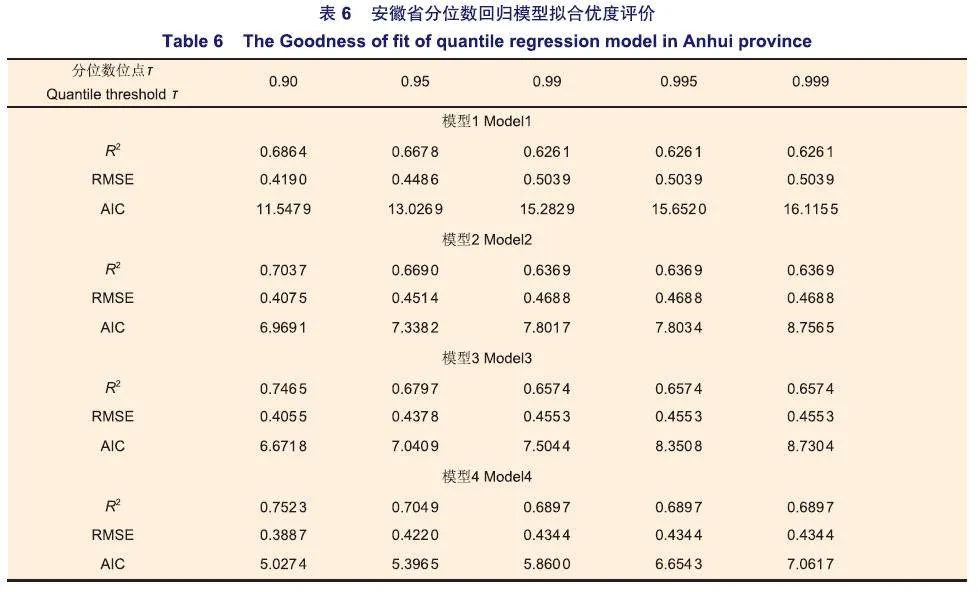
分别采用0.90、0.95、0.99、0.995和0.999分位点，拟合林分密度与林分平均胸径的数量关系。结果表明，在0.90、0.95和0.99分位点区间内，基础模型1的截距拟合数值随分位数T增加逐渐增大，自疏斜率拟合数值随分位数T的增加逐渐减小；而在0.99、0.995和0.999的分位点区间内，截距和斜率拟合参数不再随着分位数r的增加而增大（表4-6）。

基础模型1拟合R2T均在0.59以上，福建、江西和安徽省的RMSE分别介于0.55～0.77、0.37～0.57和0.42～0.50之间，各模型拟合精度相对较高。各分位数回归模型评价指标也表现出一定的规律性，R2T随分位数增加呈下降趋势，RMSE和AIC则呈上升趋势。当分位点T=0.90时，分位数回归模型R2T最大，RMSE和AIC最小，拟合效果最好，为最优模型。

2.2 混交对杉阔混交林自疏线的影响

（1）线性回归

与基础模型1相比，在添加树种混交因子后，模型2拟合得到的自疏斜率更小，即随杉木比例增加，活立木数量增加，自疏斜率轨迹也基本一致，未偏离-1.605。在模型2中，混交比例每增加1个单位，福建、江西和安徽省的林分密度分别增加0.002、0.037和0.049个单位。添加混交比例因素后，模型2拟合Radj2增加，RMSE降低，这表明模型2优于基础模型1（表2）。

（2）随机边界分析

相比基础模型1，添加混交比例因素后，随机边界分析拟合模型2得到的自疏线截距小幅增加，斜率更加平缓，但其置信区间仍包含理论值-1.605。随混交比例增加，福建、江西和安徽省林分密度分别增加0.002，0.040和0.080个单位。

（3）分位数回归

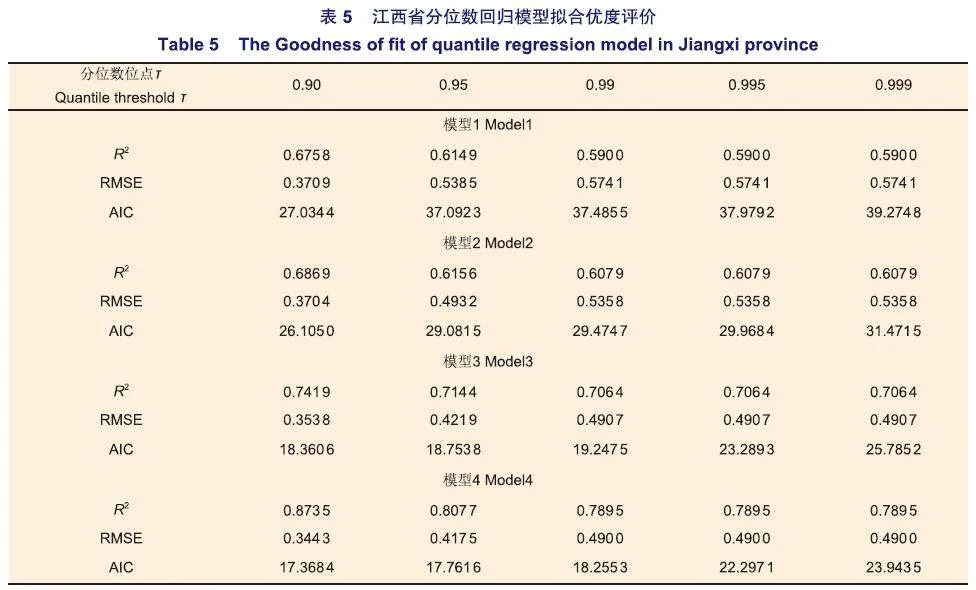
相比基础模型1，添加混交比例因素后，采用分位数回归拟合的模型2中，截距和斜率值均有所增加，但斜率变缓，且未超出理论值范围。同时，随混交比例增加，林分密度也相应增加，混交比例每增加1个单位，福建、江西和安徽省林分密度分别增加0.055～0.068、0.009～0.073和0.073～0.135个单位（表4-6）。

在加入混交比例因素后，模型2的R2T均优于基础模型1，福建省R2T从0.72提高到0.75（表4），江西省R2T从0.59提高到0.61（表5），安徽省R2T从0.63提高到0.64（表6），且拟合误差均低于基础模型1，这表明模型2优于基础模型1。另外，添加混交比例因素后，最优模型仍出现在分位值T=0.90上。

2.3 纬度对杉阔混交林自疏线的影响

（1）线性回归

采用加权最小二乘法拟合模型3发现，低纬度省份林分密度高于高纬度省份。纬度每增加1个单位，福建、江西和安徽省林分密度分别降低1.267、1.152和0.862个单位。同时，随纬度增加，自疏线逐渐变得陡峭，但其斜率置信区间仍包含-1.605。添加纬度变量后，模型拟合精度进一步提高（表2）。

（2）随机边界分析

随机边界分析拟合模型3的结果与线性回归模型拟合结果基本一致。随纬度增加，自疏斜率变陡，但福建、江西和安徽各省林分密度降低程度，与线性回归模型拟合结果有所不同，分别为1.156、1.197和0.864个单位。各省自疏斜率置信区间均包含-1.605（表3）。

（3）分位数回归

采用分位数回归拟合模型3发现，拟合截距值增大，自疏斜率值变小，纬度参数为负值，即随纬度增加，林分密度会减少。本研究中，纬度每增加1个单位，福建、江西和安徽省林分密度分别减少1.902～2.077、2.003～2.762和1.806～2.395个单位（表4-6）。

在加入纬度因素后，模型3的R2T优于模型2，福建省从0.75提高到0.77（表4），江西省从0.61提高到0.71（表5），安徽省从0.64提高到0.66（表6），且拟合误差均低于模型2，这表明模型3的拟合结果优于模型2。添加纬度因素后，分位值T=0.90时拟合模型为最优模型（表4-6）。

2.4 立地条件对杉阔混交林自疏线的影响

（1）线性回归

与添加纬度变量类似，立地条件对林分自疏斜率具有负向影响，但其作用强度小于纬度因素（表2）。在模型3基础上，添加立地变量，模型4斜率进一步变陡。福建、江西和安徽省林分密度，随立地条件增加，分别降低0.030、0.013和0.015个单位。但添加立地条件后，模型拟合精度最高，拟合模型为最优模型。

（2）随机边界分析

在添加纬度变量的模型3基础上，再次添加立地条件后构建的模型4，采用随机边界分析拟合后发现，模型4拟合截距小幅度增加，斜率进一步变陡。立地条件与纬度变量一致，均与林分密度呈负相关。立地条件每增加1个单位，福建、江西和安徽各省份林分密度分别降低0.030，0.005和0.027个单位（表3）。

（3）分位数回归

添加立地条件因素后，采用分位数回归拟合模型4发现，自疏线截距值增大，自疏斜率值变小，自疏斜率进一步变陡，但其置信区间包含-1.605。立地变量参数值为负数，即随立地条件增加，林分密度相应减少。本研究中，立地条件每增加1个单位，福建、江西和安徽各省林分密度分别减少0.017～0.029、0.014～0.025和0.021～0.027个单位（表4-6）。

在加入立地条件因素后，模型4的R2T优于模型3，福建省从0.77提高到0.78（表4）。江西省从0.71提高到0.79（表5），安徽省从0.66提高到0.69（表6），且拟合误差均低于模型3，这表明模型4的拟合结果优于模型3。添加立地条件因素后，分位数值T=0.90为分位数模型的最优分位点（表4-6）。

2.5 线性回归、随机边界分析和分位数回归（0.90、0.95和0.99分位点）拟合林分自疏线的差异

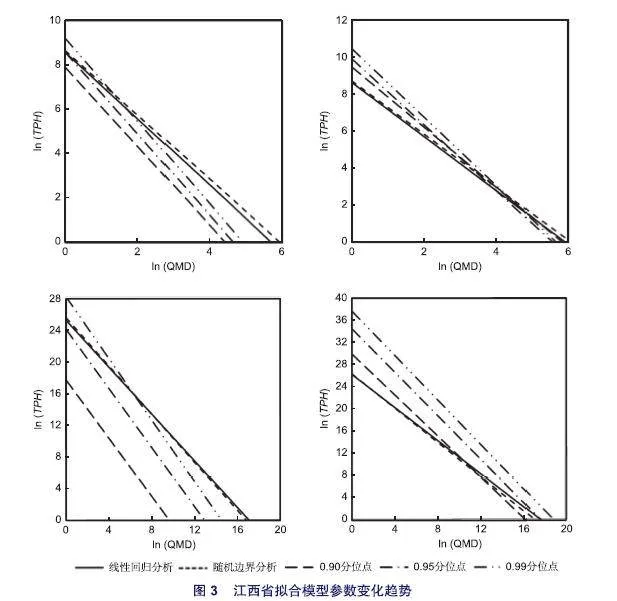
不管采用何种拟合方式，拟合模型斜率置信区间均包含-1.605，未偏离Renieke理论值。与基础模型1相比，各变量对拟合模型截距项的影响一致，在基础模型1中分别添加混交比例、纬度和立地条件因素，均使模型截距值增大；对自疏斜率来说，混交比例使其斜率值减小（自疏线平缓），而纬度和立地条件使其增大（自疏线陡峭）（表2-6）。需要指出的是，同一模型不同拟合方式，得出的模型参数各不相同。相比于随机边界分析，线性回归分析拟合截距较小，斜率较缓；随着分位点增大，分位数回归拟合截距由最小逐渐增大，斜率由最缓逐渐变最陡（图2-4）。

3 讨论

3.1 杉阔混交林林分自疏线的变化

林分可利用生境资源和相邻树木间的相互作用，决定了林分密度—生长关系。在杉阔混交林中，杉木位于林冠上层，天然更新的阔叶树位于林冠下层。随自疏混交林的生长发育，阔叶树种所需的生长空间和生境资源不断增加，林木间的不对称竞争加剧，生长空间限制和林下光照不足，均对林分内活立木数量产生了持续影响。同时，杉木持续自疏和阔叶树的持续生长更新，也导致混交林生长发生改变。本研究结果表明：杉阔混交林的自疏轨迹位于纯林自疏轨迹上方，但自疏斜率较理论值平缓。这意味着，杉阔混交林内不同树种间具有一定的互补作用，为阔叶树种更新提供有利条件，使得林分密度增加。

另外，福建、江西和安徽各省混交林自疏斜率值置信区间均包含-1.605，与同龄纯林自疏轨迹基本一致。以杉木为主的杉阔异龄复层混交林，之所以遵循理论自疏线轨迹，主要有以下两个原因：（1）林分密度存在动态负反馈调节机制，在杉木自疏过程中，上层杉木生境资源占有优势不断扩大，导致下层部分更新阔叶树不断死亡，只有少数阔叶树可以存活和生长，林分密度不会大幅度增加；（2）杉木自疏改善了下层更新树木的光照条件，客观上也促进了阔叶树种的径向生长，混交林分的径向生长也得到相应提升。杉阔混交林的林分密度和平均直径较杉木纯林均有小幅增加，但二者之间的变化趋势并没有发生显著变化。

3.2 混交对杉阔混交林林分自疏线的影响

添加混交变量后，林分自疏轨迹向上移动。这表明混交林的林分密度和径向生长量较杉木纯林均有所增加。在杉木纯林转变为杉阔混交林的过程中，杉木被压木死亡所形成的林隙为阔叶树种天然更新创造了条件。在杉阔混交林中，杉木自疏形成的林隙，可改善下层阔叶树的生长空间条件。同时，杉木林树冠水分截留量减少，大气降水可通过林隙直接进入土壤，提高土壤水分供给和养分分解效率。光照、水分和养分等可利用生境资源的增加和生长空间的改善，为林分生长潜力释放提供了条件。因此，杉阔混交林内活立木数量和生长量都有所提高，二者的自疏轨迹也就相应向上移动。

3.3 纬度差异对杉阔混交林林分自疏线的影响

研究表明：气温和降水对林分密度-生长具有显著影响。不同纬度地区的气温和降水差异，与树种存活和生长都有密切关系。在高纬度地区，树木生长主要受温度限制。随纬度降低，树木生长则受水分限制。本研究发现，在相同条件下，福建省杉阔混交林径向生长量明显高于江西省和安徽省的生长量。这表明，降水量是影响杉阔混交林生长发育的主要因素。

在水分充足的地区，温度是影响林分生长的主导因素。本研究发现，年平均温度随纬度降低而升高，混交林自疏斜率值降低，即随纬度降低，林分密度增加，尤其是当水分供应充足时，年平均温度升高会提高混交林密度。因此，随纬度增加，气温和降水条件相对较差，对林分树种更新和生长产生限制，混交林自疏斜率值也会降低。

3.4 立地条件对杉阔混交林林分自疏线的影响

立地条件较好的林分生长发育进程较快，林分可快速进入郁闭状态，林木间竞争强度也渐趋激烈。本研究中，福建省杉阔混交林立地条件普遍优于安徽和江西省的立地条件，在自疏林隙内天然更新的活立木数量也相应较多。

随立地条件增加，混交林自疏线轨迹平缓。这是因为，在杉木纯林自疏过程中，上层杉9fe471e5fe2873e022f4960b214c1372929750bf8fba7b931a0554bc1db11b51木将更多的生物量用于树冠生长，有利于获取光照，最终导致被压木死亡。尤其是良好立地的林分，被压杉木死亡数量增多，而林隙更新阔叶树尚处于幼龄期，林分直径生长量平均值增加量有限，导致较好立地的杉阔混交林自疏斜率较缓。

3.5 线性回归、随机边界分析和分位数回归拟合混交林自疏线的差异

相较于随机边界分析和分位数回归，线性回归分析假定自变量与因变量的关系是单向性的，并且假定自变量的误差方差为0，而在实际的林分测算过程中0误差不可能存在，导致斜率估计值较低。分位数回归可降低拟合过程中对极端数据的敏感性，但分位点数值仍需主观确定，在统计分析上较难反应客观真实。随机边界分析既不需要筛分拟合数据，又不涉及分位点数值主观选择，对林分自疏线估计相对客观。

本研究中，分位数回归拟合轨迹位于随机边界分析和线性回归分析拟合轨迹上方，这主要是由于线性回归分析拟合轨迹是从观测数据“中间”穿过，其实质是林分平均密度，而非林分最大密度。至于分位数回归拟合轨迹位于最上方，这主要是因为随分位点数值增大，拟合轨迹所选择的拟合数据点很可能包含极端值，导致其轨迹上移。因此，随机边界分析更适合用于拟合混交林的最大密度线。

4 结论

相较于杉木纯林，杉阔混交林自疏轨迹呈现整体上移且趋于平缓的趋势，但自疏斜率未偏离-1.605。杉阔混交林自疏轨迹随混交比例增加而增大，随纬度和立地条件增大而降低，自疏轨迹整体变化是混交比例、纬度和立地条件综合变化的结果，以上研究结论为确定混交林最大林分密度和林分密度调控措施提供了理论和技术依据。随机边界分析可以避免主观选择自疏拟合数据的影响，可以正确反映混交林自疏进程，是混交林最大密度线的最佳拟合方法。

（责任编辑：崔贝）

基金项目：国家重点研发计划项目（2021YFD2201303-03）