基于随机场模型的土石坝失效概率分析研究进展

摘 要：土石坝内部岩土体物理力学参数具有较强的空间变异性，随机场模型能够通过科学的方法对其进行准确建模和失效概率分析，有助于更好地评估大坝渗流、稳定和抗震性能。回顾了随机场模型的相关理论，总结了以往研究中常用的协方差和自相关函数，介绍了7种随机场模型的生成方法及其优缺点，并对随机场统计特征的含义进行了说明。从渗流、稳定、静力和动力分析4个方面综述了随机场模型在土石坝失效概率分析中的国内外应用实例，包括获取更准确的渗流、稳定和静动力计算结果，分析土石坝材料参数的敏感性，以及对于参数反演问题和建立大坝监控模型等方面的重要作用。未来的研究包括考虑非达西渗流、三维精细化建模以及应用新的采样技术等。相关成果可为基于随机场模型的土石坝失效概率分析研究提供参考。

关键词：随机场；土石坝；空间变异性；失效概率分析

中图分类号：TV41 文献标识码：A 文章编号：1001-9235（2024）10-0114-10

Research Progress on Failure Probability Analysis of Earth-Rockfill Dams Based onRandom Field Models

WANG Wei， LIAO Zhihao， LIAO Jielin

（Guangzhou Pearl Institute Engineering Survey and Design Co.， Ltd.， Guangzhou 510610， China）

Abstract： The physical and mechanical parameters of rock and soil inside earth-rockfill dams have strong spatial variability. Random field models can accurately model and analyze failure probability through scientific methods， which helps to better evaluate dam seepage， stability， and seismic performance. This paper reviewed relevant theories of random field models， summarized commonly used covariance and autocorrelation functions in previous research， introduced se0ba63abc964c3cad56a91b0e9e0a6ec4ea9b78ce09d1be7dcdcffd3592bd957bven methods for generating random field models and their advantages and disadvantages， and explained the meaning of random field statistical characteristics. This paper summarized domestic and international application examples of random field models in failure probability analysis of earth-rockfill dams from four aspects： seepage， stability， static， and dynamic analysis， including obtaining more accurate seepage， stability， and static dynamic calculation results， analyzing the sensitivity of material parameters of earth-rockfill dams， and playing an important role in parameter inversion problems and establishing dam monitoring models. Future research includes considering non-Darcy flow， 3D fine modeling， and applying new sampling techniques. The relevant achievements can provide a reference for the failure probability analysis of earth-rockfill dams based on random field models.

Keywords： random field; earth-rockfill dam; spatial variability; failure probability analysis

土石坝是世界上应用最广泛的一类坝型，具有适应性强、施工周期短、建设成本低等优点。受多种因素的综合影响，土石坝内部岩土体物理力学参数具有较强的空间变异性［1］。首先，地质构造、岩石类型和成因等因素会影响岩土体内部的结构和性质，导致其非均质化。其次，岩土体在沉积过程中受到水流、风化、侵蚀等自然力的作用，会导致不同深度的土层性质差异。同时，岩土体还会受到外界荷载的作用而发生变形，导致内部结构的变化。最后，在工程施工中，开挖回填也会导致岩土体结构受到干扰和变形。通过科学的方法对土石坝空间变异性进行准确建模和失效概率分析，有助于更好地评估土石坝的渗流、稳定和抗震性能。

随机场模型作为一种有效的数学工具，已经被广泛应用于土石坝工程的失效概率分析研究中［2］。随机场模型可以通过对材料参数（如渗透系数、抗剪强度、内摩擦角等）进行随机建模来描述土石坝的材料性质和空间变异特性，结合蒙特卡洛模拟分析渗流、稳定及静动力响应等指标的敏感性和概率分布，确定关键参数和敏感区域，有助于识别潜在的破坏机制和可能导致大坝安全问题的因素，评估不同概率水平下土石坝的失效风险［3-5］，从而制定相应的风险管理策略。此外，通过对材料参数进行随机场模拟，还可以生成多个可能的大坝运行场景，并对建筑物的性态进行模拟和预测，进而指导监测和改进土石坝的控制措施。

随机场模型的引入为土石坝工程领域带来了新的研究思路和方法，促进了土石坝数值计算的技术创新，推动了行业的进步和发展。本文总结了随机场模型的相关理论，综述了随机场模型在大坝渗流、稳定、静力和动力分析中的应用，展望了未来随机场在土石坝失效概率分析中的研究方向，旨在为土石坝失效概率分析研究提供全面参考，促进土石坝工程的安全设计和可靠运行。

1 随机场理论概述

1. 1 随机场的定义

随机场是概率论和统计学中的一个重要概念，用于描述具有空间或时间相关性的随机变量的集合，它可以被视为在空间或时间上分布的一组随机变量［6］。由样本空间Ω={0，1，. . .，G- 1}n取样构成的随机变量Xi所组成的S={X1，. . .，Xn}，若对所有的ω∈Ω，π（ω） > 0均成立，则称π为1个随机场。

对于离散的随机场，假设存在一个由离散随机变量组成的集合或格点网络，每个随机变量都与某个格点相关联，这些随机变量在不同的格点上服从不同的概率分布，并且彼此之间可能存在相关性［7］。对于连续的随机场，考虑定义在连续空间或时间域上的随机变量集合，通常使用概率密度函数来描述随机场的概率分布，并通过相关函数（如协方差函数）来描述不同位置之间的相关性［8］。土石坝工程中的岩土体材料参数如土层强度、密实度、渗透系数等通常具有空间变异性，即在空间上存在不规则的变化。随机场模型可以用来描述这种变异性的规律，帮助工程师了解不同位置处材料性质的差异，从而更准确地评估工程风险。

1. 2 空间相关性

空间相关性是指在空间中相邻位置的随机变量之间存在某种关联或依赖关系，当一个位置的随机变量值发生改变时，其附近位置的随机变量值也可能发生相应的变化［9-10］。在土石坝工程中，如果岩土材料参数在空间上具有较强的相关性，那么意味着相邻位置的材料性质可能会有较大的相似性。在随机场模型中，空间相关性通常通过相关函数来描述，相关函数衡量了不同位置之间的相似性或相关程度，常见的相关函数包括协方差函数和自相关函数。

协方差函数表示两个位置随机变量之间的协方差与它们各自方差之间的比例关系。当协方差函数的值大于零时，表示2个位置之间存在正相关性；当协方差函数的值小于零时，表示2个位置之间存在负相关性；当协方差函数的值等于零时，表示2个位置之间不存在线性关系［11］。随机场常用协方差函数及特点见表1。

自相关函数衡量了一个位置上随机变量与该位置周围其他位置随机变量之间的相关性，通常表现为随距离增加而递减的趋势，即距离越远，相关性越低［12］。随机场常用自相关函数及其特点见表2。

1. 3 随机场模型的生成

1. 3. 1 旋转带法

旋转带法用于生成具有平稳空间相关性的随机场，其基本思想是将二维或三维空间划分为一系列旋转的带状区域，然后在每个带状区域内生成相互独立且具有平稳空间相关性的随机变量［13-14］。在生成随机变量时，可以利用傅里叶变换将空间相关性转化为频率相关性，然后通过设定频谱密度函数来控制空间相关性的特征［15-17］。旋转带法的优点是计算效率较高，然而，对于非平稳空间相关性和复杂空间结构的情况，效果可能不理想。

1. 3. 2 谱方法

谱方法是一种基于频域分析的数值计算方法，常用于解决偏微分方程、信号处理和随机过程等问题［18-20］。该方法利用傅里叶变换或其他相关变换将问题从时域或空域转换到频域，通过对频率成分进行分析和处理，得到问题的解或近似解，可以用于生成具有所需空间相关性的随机场［21-22］。谱方法生成随机场具有多种优势，包括精度高、易于实现并行计算和可扩展性强等，然而，谱方法仅适用于具有平稳空间相关性的随机场。

1. 3. 3 矩阵分解法

矩阵分解法使用一组基函数来表示所需随机场，通过拟合样本数据，可以计算出每个基函数的系数，使用所选择的概率分布函数生成随机变量，将生成的随机变量与基函数的系数相乘并求和，即可得到所需随机场的一个实现［23-24］。矩阵分解法是一种基于矩阵运算的数值方法，其算法实现相对简单，易于应用和扩展，缺点是只能处理具有简单空间相关性的随机场［25-26］。

1. 3. 4 Karhunen-Loeve展开法

Karhunen-Loeve展开法基于随机场的统计特性，使用已知样本数据或一些经验数据，计算随机场的协方差函数或自相关函数，对其进行特征分解得到一组特征值和对应的特征函数，根据特征值的大小选择保留最重要的特征，生成一组独立同分布的正态随机变量，将生成的随机变量与保留的特征函数相乘并求和，即可得到所需随机场的一个实现［27-30］。Karhunen-Loeve展开法的优势在于它能够提供一种有效的降维技术，可以通过保留较少数量的特征来近似描述整个随机场，提高随机场生成的效率。然而，该方法通常假设随机场服从高斯分布，对于非高斯分布或复杂空间相关性的随机场效果不佳［25，31］。

1. 3. 5 移动平均法

移动平均法通过使用1个窗口在样本数据上滑动，从第一个位置开始，计算窗口内数据的平均值，并将其作为生成的随机场的一个实现［32-35］。然后，向右移动窗口，重复此过程，直到覆盖整个空间。窗口大小决定了空间相关性的尺度，较小的窗口会产生更细节化和局部化的随机场，而较大的窗口会产生平滑且整体性较强的随机场。移动平均法生成的随机场具有平滑的特性，然而，在应用中需要注意边界效应和长度相关性的限制。

1. 3. 6 序贯模拟法

序贯模拟法基于模拟样本路径的思想，在空间范围上设置一些采样点，作为样本路径的起点，确定样本路径在空间中的前进方向。依次沿着样本路径方向，根据已知的样本数据和空间相关性，模拟出每个采样点处的随机场值。通过调整样本路径和参数设置，可以获得不同尺度、形态和相关性的随机场实现［36-38］。序贯模拟法的优势是可以用于模拟一些非线性或非高斯分布的随机场，然而在计算过程中可能存在计算量大、计算时间长等问题。

1. 3. 7 局部平均法

局部平均法通过在空间范围上创建一个初始的规则网格，计算每个网格点周围邻居点的随机场平均值，作为该点的局部平均值，将初始网格细分为更小的网格，计算每个新网格点处的局部平均值，通过不断地细分网格和计算局部平均值，生成具有不同尺度和空间相关性的随机场［39-41］。局部平均法在边界处可能存在一些偏差，因为在边界上没有足够的邻居点进行平均计算。此外，网格细分的程度和细分算法的选择会影响生成随机场的精细程度和准确性。

在进行土石坝失效概率分析时，选择合适的随机场生成方法是1个综合性问题，需要结合数据特性、计算复杂度、精度要求等多方面考虑。可根据工程实际需求和可接受的计算复杂度，在精度和计算效率之间进行权衡，选择适当的随机场生成方法，达到事半功倍的效果。

1. 4 随机场的统计特性

随机场的统计特性是指描述和表征随机场性质的一组统计量或属性，包括均值、变异系数、相关距离、概率分布等［42］。在土石坝工程中，随机场的均值是指岩土材料参数在每个空间位置上的平均值，是进行工程设计和分析的基础。随机场的变异系数代表了岩土材料参数的离散程度相对于其均值的大小，反映了材料性质在空间上的不均匀性。随机场相关距离是描述岩土材料参数空间相关性的尺度，它表示在一定距离内，岩土体性质之间的相关性较高，超过该距离后相关性逐渐减弱至接近零［43］。随机场的概率分布描述了岩土材料参数值出现的频率和可能性，常见的概率分布包括正态分布、对数正态分布等。

1. 5 土石坝工程中随机场模型参数的选取

选择合适的随机场模型参数对于土石坝失效概率分析至关重要。首先，需要收集与工程相关的地质勘探数据，通过对这些数据的分析，了解岩土体性质的空间变异性和相关性，包括均值、变异系数、相关距离等信息。然后，根据数据分析的结果，选择适合描述岩土体性质空间变异性的概率分布函数。最后，建立数值模型，根据实际监测数据验证所选参数的准确性和适用性。确定随机场模型参数是一项复杂的任务，在实际工程中往往无法获取足够和高质量的地质勘探数据，无疑会增加模型建立的难度，可以借助工程类比、专家咨询或相关文献资料等资源，进行综合分析和判断，以选择最合适的随机场模型参数。

2 随机场模型在土石坝失效概率分析中的应用

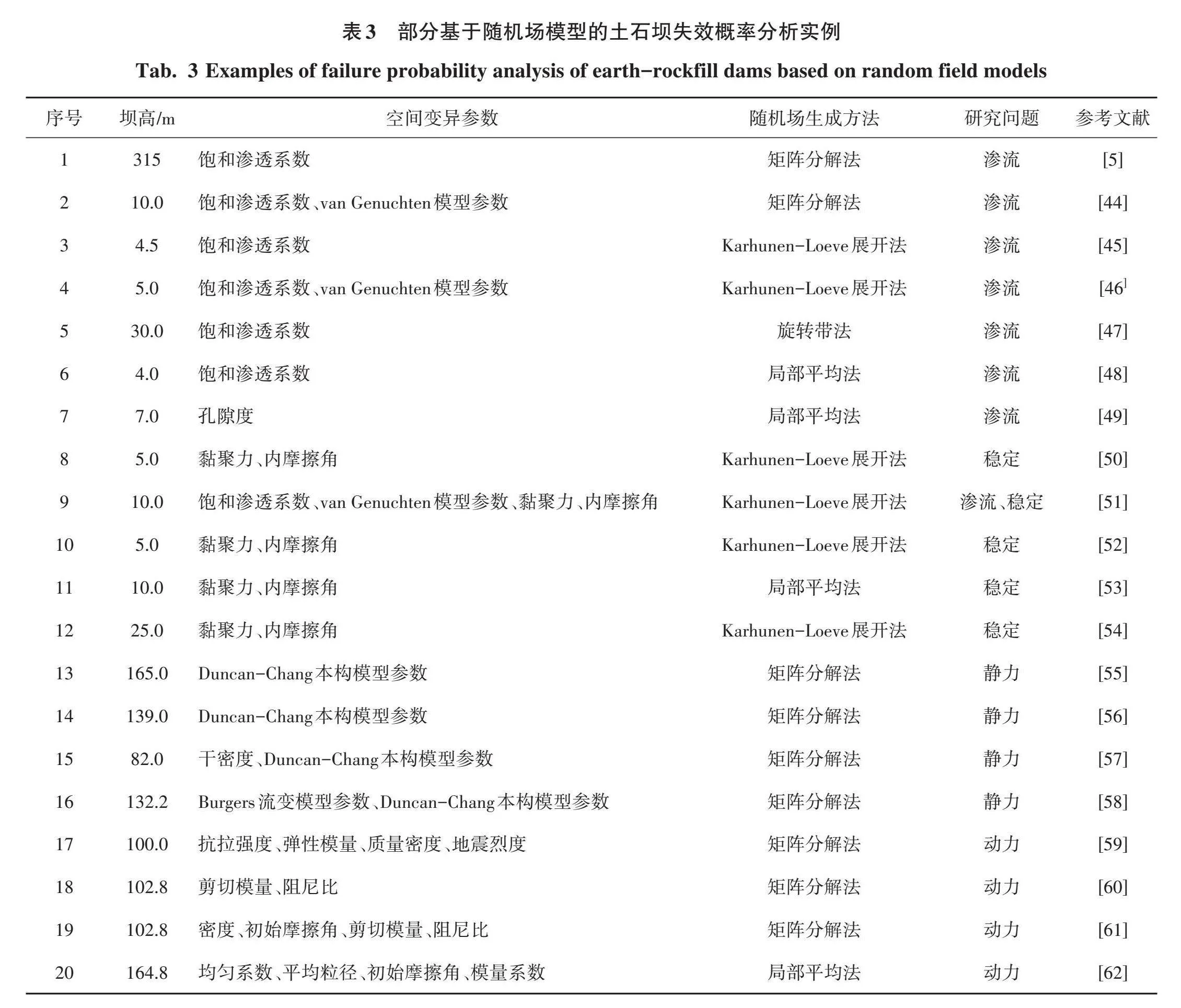
土石坝工程受到材料参数空间变异性等不确定因素的影响，随机场模型能够综合考虑这些不确定性，通过概率分析得到不同条件下的水力坡降、稳定性指标、应力响应、振动响应等概率分布特性，有助于工程师更全面地了解土石坝在不同情况下的行为特性，从而指导工程设计和管理决策。近年来，国内外学者基于随机场模型在土石坝渗流稳定和静动力分析方面进行了大量研究，部分研究实例总结见表3。

2. 1 渗流分析

使用随机场模型来考虑土石坝渗流参数的空间变异性和随机性，可以获取更准确的渗流预测结果。例如，黄伟杰等［5］为探究某超高心墙堆石坝防渗材料空间变异性对渗流安全的影响，建立了随机渗流分析模型，对大坝渗透系数进行空间离散，系统研究了渗流控制指标的演变规律，发现忽略防渗体的空间变异性会高估大坝的渗流安全状态。

随机场模型还可以用于分析土石坝渗流参数的敏感性，并识别对渗流响应量贡献最大的关键参数。例如，Tan等［44］采用van Genuchten模型描述堤坝材料的土水特征曲线，通过矩阵分解法生成水力参数的对数正态随机场，研究了不同水力参数变异性和相关性对堤坝渗流量的影响，结果发现相较于van Genuchten模型拟合参数，饱和渗透系数的变异性对渗流量有更显著的影响。

自相关函数衡量了土石坝渗流参数的空间变化，选择合适的函数形式对于随机渗流分析至关重要。例如，Liu等［45］采用随机有限元法研究了自相关函数类型对堤坝渗流的影响，发现平方指数型自相关函数对于渗流量的计算结果更偏保守，而单指数型自相关函数对于水力梯度的计算结果更偏保守。

传统平稳随机场假设整个研究区域的材料参数统计特征是恒定的，忽略了岩土参数的各向异性。为克服这一缺陷，一些学者考虑工程实测数据，使用参数均值随深度变化的条件随机场或非平稳随机场来描述土石坝构造的空间变异性。例如，Chi等［46］比较了经典平稳随机场，条件随机场和非平稳随机场对土石坝渗流概率分析结果的影响，发现不同渗透系数随机场的渗流分析结果存在一定差异，稳定随机场分析结果的离散度最大，条件随机场分析结果的离散度最小，这种差异对于流速最为显著，其次是水力梯度，对于孔隙压力不太显著。

2. 2 稳定分析

土石坝边坡失稳是其重要破坏模式之一，传统的确定性分析方法没有合理考虑参数空间变异性，计算结果往往偏离客观实际，概率分析能够有效克服这一缺陷。例如，肖金红等［50］以安全系数和失效概率为评价指标，考虑土石坝材料的空间变异性，建立随机场模型对其边坡稳定进行概率分析，发现与确定性分析相比，土石坝安全系数降低，失效概率提高，边坡稳定性分析结果更加合理。

随机场模型还可以用于分析土石坝边坡稳定参数的敏感性，并识别对边坡失稳影响最大的关键参数。例如，为了有效分析考虑空间变异性的土石坝边坡稳定问题，蒋水华等［51］发展了土石坝边坡可靠度非侵入式随机分析方法，并通过参数敏感性分析探讨了饱和渗透系数、黏聚力及内摩擦角变异性对土石坝边坡稳定的影响，研究发现土石坝边坡失效概率与3个参数的变异系数之间呈正相关，其中黏聚力变异性的影响最显著，饱和渗透系数变异性的影响最不显著。

土石坝边坡的可靠度分析通常需要进行大量的数值计算，这些计算非常耗时，采用代理模型可以通过对原始模型进行合理的简化和逼近，从而显著减少计算量，提高计算效率。例如，邓志平等［52］为准确高效地开展小失效概率的边坡可靠度分析，在考虑材料参数空间变异性的前提下，提出了一种基于分段逆回归的主动学习多元自适应回归样条法与子集模拟结合的边坡可靠度分析方法，不仅增加了计算结果的精确度，而且避免了内存溢出情况。

土石坝材料参数的空间变异性在水平方向和垂直方向上的差异显著，将土性参数的空间分布模拟为各向异性随机场，可以得到更为精确的计算结果。例如，舒苏荀等［53］利用各向异性随机场模拟土性参数的空间变异性，将有限元法和蒙特卡洛模拟相结合，计算各参数组合对应的可靠度指标，发现与水平方向的空间变异性相比，垂直方向的空间变异性对边坡可靠度的影响更为显著。

2. 3 静力分析

材料参数的空间变异性会导致土石坝体内部的应力和变形分布具有差异性，考虑空间变异性可以更真实地模拟土石坝的实际情况，提高静力计算结果的准确性。例如，Chen等［55］通过大规模三轴试验，确定了大坝压实质量与Duncan-Chang本构模型参数的定量关系，并基于这种发展关系，得到力学参数的约束随机场进行有限元静力计算，发现考虑土体材料的空间变异性能够得到更接近实际情况的应力和变形计算结果。

合理定义随机场模型的统计特征是获得准确计算结果的前提，然而土石坝材料参数的实测数据往往较难获取，反分析是解决这一问题的有效手段。例如，杨杰等［56］将相关向量机与随机有限元相结合， 对面板堆石坝材料参数的变异系数进行不确定性反分析，通过对面板堆石坝应用实例进行计算，证明所建立的不确定性反分析模型综合考虑了数值计算以及输入-输出间的不确定性，可快速、精确地确定筑坝材料参数的变异系数。

随机场模型还可以用于分析土石坝静力学参数的敏感性，并识别对大坝应力和变形影响最大的关键参数。例如，Chi等［57］根据原位监测值确定土壤干密度的自相关距离和分布函数，利用三轴试验结果建立干密度与Duncan E-B模型参数之间的回归函数，根据干密度分布函数和回归函数确定E-B模型参数的累积分布函数，并采用等概率变换方法建立土壤参数随机场进行土石坝静力计算，并讨论了E-B模型参数的敏感性，发现Kb对随机有限元计算结果的影响最大，Rf对随机有限元计算结果的影响最小。

土石坝安全监控模型能够通过分析监测数据，准确预测大坝力学性态，为大坝安全评价提供参考，随机场模型在该领域也被广泛应用。例如，Ran等［58］为进一步提高大坝监控模型的预测精度，增强监控指标确定方法的合理性，考虑堆石材料空间变异性对大坝位移的影响，基于随机有限元法建立了一种新的堆石坝位移监控混合模型，提出了一种多指标合并的堆石坝位移监控混合指标确定方法，实例分析表明所提模型和指标确定方法科学合理且精度显著提高。

2. 4 动力分析

地震是土石坝安全性评估的重要因素之一，考虑空间变异性对于大坝地震响应特性的分析和抗震设计具有重要意义。例如，Chen等［59］以某100 m高的土石坝为例，考虑填土质量密度、杨氏模量和抗拉强度的非均质性，采用随机有限元方法进行动力响应计算，研究了土石坝地震响应与材料参数具体空间分布的关系，研究结果证实了在土石坝地震评估中考虑填料参数空间变异性的重要性。

随机场模型还可以用于分析土石坝动力学参数的敏感性，并识别对大坝动力响应影响最大的关键参数。罗博华等［60］将空间随机场模拟技术与有限元方法相结合，选取土石坝动力随机参数进行敏感性分析，研究发现对加速度放大系数而言，阻尼比随剪应变变化的参数、最大动剪切模量的参数和最大阻尼比的敏感性较高，对计算结果影响显著；对永久变形而言，阻尼比随剪应变变化的参数、最大动剪切模量随围压变化的参数和泊松比的敏感性较高。

除了土石坝体本身，覆盖层土体类型复杂，结构松散，有时存在透镜体，材料参数同样具有较强的空间变异性，地震作用下对坝基防渗墙应力变形的影响引起了许多学者的重视。例如，Song等［61］考虑覆盖层材料参数的空间变异性和相关性，研究了静力和动力参数随机性对沥青心墙坝地震响应的影响，发现材料参数的空间变异性对峰值加速度的影响大于对大坝永久变形的影响，且覆盖层响应的离散度大于坝体和沥青心墙。

3 结论与展望

随机场模型可以通过对材料参数进行随机建模来描述土石坝的空间变异特性，从而获取更准确的渗流稳定和静动力计算结果，还可以用于分析土石坝材料参数的敏感性，识别对大坝响应影响最大的关键参数，此外，对于解决参数反分析问题和建立大坝监控模型也起到了至关重要的作用。在利用随机场模型进行土石坝概率分析的领域，尽管国内外学者已经进行了大量研究并取得了显著成果，但仍存在诸多不足之处，可以考虑从以下3个方面开展未来的研究。

a）在土石坝渗流概率分析中，以前的大多数研究都是基于层流和达西定律的假设，然而，土石坝在使用过程中会受到荷载、水位、地震等多种因素的影响，坝体可能会发生变形和裂隙发育，这些因素会导致坝体的渗透性发生改变，从而使渗流规律与达西定律不一致。对于未来的研究，可以考虑非达西流的假设，通过孔隙度和土壤颗粒直径等变量的随机性来进行非达西渗流的概率分析。

b）土石坝失效概率分析往往基于二维随机场，忽视了三维效应的影响，常规计算机算力不足是导致这一问题的主要原因。随着硬件设施水平的不断提高，在未来有必要考虑土石坝失效概率分析的三维精细化建模，与二维分析相比，其能够更加准确地描述土石坝的实际行为，提高分析的准确性和可靠性。

c）传统的采样方法，如简单的随机采样和分层采样，在处理复杂系统或高维空间时往往是无效和不准确的。新采样技术的发展，例如重要性采样、自适应抑制采样和马尔可夫链蒙特卡罗方法可以更有效地探索参数空间，更准确地进行期望值预测。除了提高精度外，新的采样技术还大大提高了精细化建模的可能性。因此，在未来的研究中，有必要结合新的采样技术进行土石坝失效概率分析。

参考文献：

［1］谢立全，于玉贞，张丙印. 土石坝坡三维随机有限元整体可靠度分析［J］. 岩土力学， 2004（S2）： 235-238.

［2］孙伟，何蕴龙，袁帅，等. 考虑材料非均质性的胶凝砂砾石坝随机有限元分析［J］. 水利学报， 2014， 45（7）： 828-836.

［3］吕鹏. 基于不确定性分析的土石坝渗流性态研究［D］. 天津：天津大学， 2019.

［4］王宝强，李伟生. 基于PSO-LHS-MC法的土石坝坝坡失稳时变风险率分析［J］. 人民珠江， 2023， 44（S2）： 109-115.

［5］黄伟杰，庞锐，徐明洋，等. 考虑渗透系数空间变异性的超高心墙堆石坝渗流分析［J］. 水利与建筑工程学报， 2023， 21（6）： 143-149.

［6］姜琪浩，王金铜，侯波，等. 考虑地层变异和参数空间变异的浅基础承载力可靠度分析［J］. 岩土力学， 2023， 44（11）：3288-3298.

［7］顾鑫，仉文岗，欧强，等. 基于Chebyshev-Galerkin-KL展开的土质边坡稳定可靠度分析［J］. 岩土工程学报， 2023， 45（12）： 2472-2480.

［8］赵超.基于随机场理论的地层类型与岩土参数空间分布耦合概率建模方法研究［D］.武汉：中国地质大学，2022.

［9］REN Y， NISHIMURA S， SHIBATA T， et al. Data Assimilation for Surface Wave Method by Ensemble Kalman Filter with Random Field Modeling［J］. International Journal for Numerical and Analytical Methods in Geomechanics， 2022， 46（15）： 2944-2961.

［10］WANG Y K， HAN M S， LI B， et al. Stability Evaluation of Earth-rock Dam Reinforcement with New Permeable Polymer Based on Reliability Method［J］. Construction and Building Materials， 2022， 320. DOI：10. 1016/j. conbuildmat. 2021. 126294.

［11］姚敬茹.岩土参数空间相关性与随机场模拟研究及应用［D］.济南：山东建筑大学，2018.

［12］刘航飞. 基于不确定性分析的高心墙土石坝渗流性态及渗透稳定可靠性研究［D］. 西安：西安理工大学， 2023.

［13］MANTOGLOU A， WILSON JL. The Turning Bands Method for Simulation of Random Fields Using Line Generation By a Spectral Method［J］. Water Resources Research， 1982， 18（5）： 1379-1394.

［14］TOMPSON AFB， ABABOU R， GELHAR LW. Implementation of the Three-dimensional Turning Bands Random Field Generator［J］. Water Resources Research， 1989， 25（10）： 2227-2243.

［15］LAUZON D， MARCOTTE D. Calibration of Random Fields by a Sequential Spectral Turning Bands Method［J］. Computers and Geosciences， 2019， 135. DOI：10. 1016/j. cageo. 2019. 104390.

［16］EMERY X， FURRER R， PORCU E. A Turning Bands Method for Simulating Isotropic Gaussian Random Fields on the Sphere［J］. Statistics and Probability Letters， 2018， 144： 9-15.

［17］LIU G H， PU H， ZHAO Z H， et al. Coupled Thermo-hydro-mechanical Modeling on Well Pairs in Heterogeneous Porous Geothermal Reservoirs［J］. Energy， 2019， 171： 631-653.

［18］CAI Z N， LIN B， LIN M X. A Positive and Moment-preserving Fourier Spectral Method［J］. Siam Journal on Numerical Analysis， 2024， 62（1）. DOI：10. 1137/23M1563918.

［19］SHEN M X， WANG H Y. An Efficient Spectral Method for the Fractional Schrödinger Equation on the Real Line［J］. Journal of Computational and Applied Mathematics， 2024， 444. DOI：10.1016. j. cam. 2024. 115774. .

［20］ALI SF， KAMRAN， KAMAL S， et al. Numerical Modelling of Advection Diffusion Equation Using Chebyshev Spectral

Collocation Method and Laplace Transform［J］. Results in Applied Mathematics， 2024， 21. DOI：10. 1016/j. rinam. 2023.100420.

［21］LANG A， POTTHOFF J. Fast Simulation of Gaussian RandomFields［J］. Monte Carlo Methods and Applications， 2011， 17（3）： 195-214.

［22］ROBIN M， GUTJAHR A， SUDICKY E， et al. Cross-correlatedRandom Field Generation with the Direct Fourier Transform Method［J］. Water Resources Research， 1993， 29（7）： 2385-2397.

［23］TIAN N， CHEN J， WANG Z S， et al. Modified MatrixDecomposition Method for Generating Multivariate Three-dimensional Cross-correlated Random Fields［J］. Arabian Journal for Science and Engineering， 2023， 48（10）： 13615-13632.

［24］LI D Q， XIAO T， ZHANG L M， et al. Stepwise CovarianceMatrix Decomposition for Efficient Simulation of Multivariate Large-scale Three-dimensional Random Fields［J］. Applied Mathematical Modelling， 2018， 68： 169-181.

［25］王占盛，陈健，戎虎仁，等. 土性参数各向异性随机场的表征与建模方法［J］. 计算力学学报，2021，38（1）：29-36.

［26］袁博. 马尔可夫随机场的空间相关模型在非负矩阵分解线性解混中的应用［J］. 计算机应用，2017，37（12）：3563-3568.

［27］李少龙，杨金忠，蔡树英. 基于van Genuchten-Mualem模型的饱和-非饱和介质流动随机数值分析［J］. 水利学报，2006（1）： 33-39.

［28］李少龙，杨金忠，张家发. KL展开在渗流场随机分析中的初步应用［J］. 长江科学院院报，2009，26（10）：39-43.

［29］史良胜，杨金忠，陈伏龙，等. Karhunen-Loeve展开在土性各向异性随机场模拟中的应用研究［J］. 岩土力学，2007（11）：2303-2308.

［30］TSANTILI I C， HRISTOPULOS D T. Karhunen-loeve Expansion of Spartan Spatial Random Fields［J］. Probabilistic Engineering Mechanics， 2016， 43： 132-147.

［31］BAIZHIKOVA Z，LE J L，BALLARINI R. Stochastic Buckling of Geometrically Imperfect Beams on Elastic Foundation［J］. Journal of Applied Mechanic， 2022， 90（1）. DOI：10. 1115/1. 4055811.

［32］ALAMANIS N， DAKOULAS P. Simulation of Random Fields of Soil Properties by the Local Average Subdivision Method andEngineering Applications［J］. Energy Systems， 2019， 12（4）： 841-861.

［33］YUAN Y L， HU C M， MEI Y， et al. Slope Reliability Analysis Based on Curvilinear Local Averaging of a 2-D Random Field［J］. Computers and Geotechnics， 2021， 137. DOI： 10. 1016/j. compgeo，2021. 104247.

［34］DENNIS L， FABIAN M， ANSGAR S. Regularity of Multifrac⁃tional Moving Average Processes with Random Hurst Exponent［J］. Stochastic Processes and Their Applications， 2021， 140： 21-48.

［35］佘跃心，张爱国. 移动平均法计算相关距离的分析与探讨［J］. 淮阴工学院学报，2003（1）：13-16， 35.

［36］LI W D， ZHANG C R. Some Further Clarification on Markov Chain Random Fields and Transiograms［J］. International Journal of Geographical Information Science， 2013， 27（3）： 423-430.

［37］张抒，唐辉明，刘晓，等. 基于饱和渗透系数空间变异结构的斜坡渗流及失稳特征［J］. 地球科学，2018，43（2）：622-634.

［38］SAFIKHANI M， ASGHARI O， EMERY X. Assessing the Accuracy of Sequential Gaussian Simulation Through Statistical Testing［J］. Stochastic Environmental Research and Risk Assessment， 2017， 31（2）： 523-533.

［39］王涛，马骏，周国庆，等. 冻土地层三维空间变异性表征及冻结帷幕温度特征值演化过程研究［J］. 岩石力学与工程学报， 2022， 41（10）： 2094-2108.

［40］豆红强，王浩. 非平稳随机场下饱和渗透系数空间变异性的无限长边坡稳定概率分析［J］. 土木工程学报，2017，50（8）：105-113， 128.

［41］胡长明，袁一力，梅源，等. 基于二维随机场在圆弧曲线上局部平均化的边坡可靠度分析［J］. 岩石力学与工程学报，2020，39（2）：251-261.

［42］于书凝，杨文东，张斌，等. 基于正态信息扩散的堤防土层渗透系数空间分布研究［J］. 水电能源科学，2024（3）：208-211，215.

［43］宋福彬.基于随机介质算法的土石坝病害模拟及特征识别方法研究［D］.西安：西安理工大学，2021.

［44］TAN X H， WANG X， KHOSHNEVISAN S， et al. Seepage Analysis of Earth Dams Considering Spatial Variability of Hydraulic Parameters［J］. Engineering Geology， 2017， 228： 260-269.

［45］LIU L L， CHENG Y M， JIANG S H， et al. Effects of Spatial Autocorrelation Structure of Permeability on Seepage Through an Embankment on a Soil Foundation［J］. Computers and Geotechnics， 2017， 87： 62-75.

［46］CHI F D， PIERRE B， CLAUDIO C， et al. Stochastic Seepage Analysis in Embankment Dams Using Different Types of Random Fields［J］. Computers and Geotechnics， 2023， 162. DOI：10.1016/j. compgeo. 2023. 105689.

［47］GUI S X， ZHANG R D， TURNER J P， et al. Probabilistic Slope Stability Analysis with Stochastic Soil Hydraulic Conductivity［J］. Journal of Geotechnical and Geoenvironmental Engineering，2000， 126（1）： 1-10.

［48］AHMED A. Stochastic Analysis of Free Surface Flow ThroughEarth Dams［J］. Computers and Geotechnics， 2009， 36（7）： 1186-1190.

［49］LE T， GALLIPOLI D， SANCHEZ M， et al. Stochastic Analysisof Unsaturated Seepage Through Randomly Heterogeneous Earth Embankments［J］. International Journal for Numerical and Analytical Methods in Geomechanics， 2012， 36（8）： 1056-1076.

［50］肖金红. 考虑土体空间变异性的土石坝稳定性分析［J］. 水利技术监督， 2020（3）： 18-20.

［51］蒋水华，刘贤，黄劲松，等. 考虑水力模型参数空间变异性土石坝边坡可靠度分析［J］. 应用基础与工程科学学报，2021，29（4）： 939-951.

［52］邓志平，钟敏，潘敏，等. 考虑参数空间变异性和基于高效代理模型的边坡可靠度分析［J］. 岩土工程学报，2024，46（2）：273-281.

［53］舒苏荀，龚文惠，王佳，等. 各向异性随机场下的边坡模糊随机可靠度分析［J］. 岩土工程学报， 2015，37（7）：1204-1210.

［54］LIZARRAGA H S， LAI C G. Effects of Spatial Variability of Soil Properties on the Seismic Response of an Embankment Dam［J］. Soil Dynamics and Earthquake Engineering， 2014， 64： 113-128.

［55］CHEN H， LIU D H. Stochastic Finite Element Analysis of Rockfill Dam Considering Spatial Variability of Dam Material Porosity［J］， 2019， 36（9）： 2929-2959.

［56］杨杰，马春辉，向衍，等. 基于相关向量机与随机有限元的筑坝材料参数不确定性反分析［J］. 中国科学：技术科学，2018，48（10）：1113-1121.

［57］CHI S C， FENG W Q， JIA Y F， et al. Stochastic Finite-elementAnalysis of Earth-rockfill Dams Considering the Spatial Variability of Soil Parameters［J］. International Journal of Geomechanics， 2022， 22（12）. DOI：10. 1061（/ ASCE）GM. 1943-5622. 0002454.

［58］RAN L， YANG J， ZHANG P L， et al. A Hybrid MonitoringModel of Rockfill Dams Considering the Spatial Variability of Rockfill Materials and a Method for Determining the Monitoring Indexes［J］. Journal of Civil Structural Health Monitoring， 2022， 12（4）： 817-832.

［59］CHEN J Y， LIU P F， XU Q， et al. Seismic Analysis of HardfillDams Considering Spatial Variability of Material Parameters［J］. Engineering Structures， 2020， 211. DOI：10. 1016/j. engstruct.2020. 110439.

［60］罗博华，宋志强，王飞，等. 考虑覆盖层地基材料空间变异性的沥青混凝土心墙坝地震响应研究［J］. 振动与冲击，2022，41（2）：53-63.

［61］SONG Z Q， WANG Z K， LUO B H， et al. Seismic Response of Asphalt Concrete Core Dam Considering Spatial Variability of Overburden Foundation Materials［J］. Arabian Journal for Science and Engineering， 2022， 47（10）： 12605-12620.