应用型大学课程思政融入高等数学的教学改革探索

摘 要：习近平总书记非常重视全国高校思想政治工作，多次作出重要指示。教育是推动民族发展、促进社会进步的重要支柱，是功在当代、利在千秋的德政工程，对于培育人才、提高民族素质、实现中华民族伟大复兴的中国梦具有决定性意义。以应用教育为目的的应用型大学着重于解决大学生的就业问题。因此，为充分体现应用型大学“工匠精神”的办学风格，响应国家号召，通过教学改革将思政教育与高数教学有机结合，以非常规教学手段实现立德树人的润物无声，将高数兴趣化融入学生日常生活，将中国优秀传统文化引入课堂，增强文化认同感。选取教学实践中的典型知识点作为案例，探究高等数学课程思政建设途径。

关键词：应用型大学；工匠精神；课程思政；高等数学；教学改革

中图分类号：G641 文献标志码：A 文章编号：2096-000X（2024）30-0136-05

Abstract： Xi Jinping， president of the People's Republic of China attached great importance to the ideological and political work in colleges and universities across the country and made important instructions for many times. Education is an important pillar for promoting national development and social progress， a moral and political project that contributes to the present and benefits the future， and is of decisive significance for cultivating talents， improving national quality， and realizing the Chinese dream of the great rejuvenation of the Chinese nation. Therefore， in order to fully reflect the"craftsman spirit" of the applied university， respond to the call of the state， organically combine ideological and political education with advanced mathematics teaching through teaching reform， realize the silent cultivation of virtue and cultivation of people through unconventional teaching methods， integrate high number interest into students' daily life， introduce excellent traditional Chinese culture into the classroom， and enhance cultural identity. Typical knowledge points in teaching practice were selected as cases to explore the ideological and political construction of higher mathematics courses.

Keywords： applied university; craftsmanship; curriculum ideology and politics; Advanced mathematics; teaching reform

基金项目：深圳技术大学教学改革项目“计算机‘101计划’背景下的数学课程教学改革的探索”（20241010）、“高等数学教学辅助手段的研究和实践”（BDI202201005）、“新时代高等数学课程教学创新的研究与实践”（BDI202301001）、“产学互增式成长型人工智能人才培养”（BDI20231015）；深圳技术大学一流课程培育项目“人工智能数学基础”（BDI202303001）；广东省高等教育教学改革项目“大数据背景下统计实践类课程教学与评估体系探索”（无编号）

第一作者简介：田卫忠（1983-），男，汉族，山东菏泽人，博士，副教授，数学系副主任。研究方向为数理统计。

21世纪以来，随着国家的发展与社会的进步，更多普通家庭的孩子有了接受教育的机会，全民素质飞速提高，国家的教育事业发展蒸蒸日上。然而，处于新时代背景下的祖国更需要的是多样化的人才。这就要求学生应兼具“德智体美劳”的全面优势，“蒙以养正，圣功也”，以课程思政作为育人渠道，将知识传授与价值引导有效融合、相互渗透，以立德树人为宗旨，有利于培养新时代下一代又一代社会主义建设者和接班人，培育拥护中国共产党领导和中国特色社会主义制度、立志为共产主义事业奋斗终身的栋梁之材。我国高等教育结构分为高职院校、应用型大学、研究型大学三大层次。应用型大学一般都具有一些各自的教学培养特色，例如深圳技术大学，作为一所广东省和深圳市高标准建设的国际化、高水平、示范性一流应用技术大学，充分借鉴和引进德国、瑞士等发达国家一流技术大学先进的办学经验，致力于培养本科及以上层次具有国际视野、工匠精神和创新创业能力的高水平工程师、设计师等高素质应用型人才[1]。同时，应用型大学应当以教学为主导、以行业为导向、以实践为依托培养高素质应用型人才，要求毕业生既能拥有技术端的专业知识，又能对接操作阶段的实战技能。在人才培养、社会服务、科学研究等方面，应用型大学应与其他大学有所区别。由此，应用型大学应结合自身办学风格和培养目标，制定符合应用型大学的思政教育实施方案[2]。

思政教育走入高校课堂的教学模式方兴未艾，迄今为止，已有多所应用型大学实现思政教育融入课堂的改革，吉林农业科技学院将专业课机械制造技术基础与思政教育结合，提高课堂活跃度的同时增强了学生的思政素质，促进了工科专业课思政教学改革[2]；武夷学院数学与计算机学院将思政融入信号与系统课程，解决学生为什么而学、如何学以致用等问题，课程内引入Matlab仿真软件培养学生理论与实践相结合的实践能力与创新能力，最后建立线上线下讨论组培养学生的表达能力和动手能力。通过教学改革，充分调动了学生学习的主观能动性[3]。本文将结合深圳技术大学“匠心筑梦，人文情怀”的校训，将思政元素引入高数课堂，提高学生学习能力的同时注入人文情怀，提高学生思想觉悟，为学校和社会的发展锦上添花。

一 思政融入课堂理论逻辑

高等数学的课程思政，是指“对高等数学的思想政治教育因素充分挖掘整合，发挥高等数学课程的育人功能，在提高学生数学思维能力的同时，提升思想政治素养，从而内化为一种素质或能力，成为个体认识世界与改造世界的基本能力方法。”[4]众所周知，思政教育是我国培养人才的基本要求，任何学科中都应该充分利用学科特点引入思政元素，在高等数学中，主要包含以下几种思政元素。

（一） 家国情怀

我国的数学在历史上发挥着举足轻重的作用，许多优秀数学家如华罗庚、陈景润、祖冲之、刘徽和秦九韶等取得的丰功伟绩为数学乃至整个人类教育事业的进步有着不可替代的作用。近代中国也涌现出许多优秀的数学家，如丘成桐、陶哲轩、张益唐、萧荫堂，亦或是近年来数学领域年轻人才韦东奕等。从古至今，不乏一批批的数学学者为数学事业添砖加瓦，通过在教学中引入我国数学家的成就可以增强民族自豪感，提高民族自信心，有效促进学生学习数学的积极性。

（二） 哲学思政

数学是一切科学的基础，数学也是哲学的基础。在数学这类现代基础学科的研究中，哲学并不是与其一分为二的，哲学可以是指导人自我生活的艺术，也可以斡旋于各种学问的研究之间。所以哲学对于数学的研究意义就在于，哲学提供某种思维方式，也可以帮助数学发现问题，哲学作为世界观，为数学提供正确的指导思想； 哲学作为方法论，为数学提供伟大的认识工具和探索工具。高等数学中的许多知识点例如积分与微分、收敛与发散等，这些看似相悖的知识点之间又存在着部分联系。这就要求我们在处理问题时应该用发展的眼光看待问题，具体问题具体分析，从中培养学生科学严谨的逻辑思维。

（三） 工匠精神

学习高数是一个需要持之以恒的过程，高等数学知识体系的细节繁多，尤其是各种定理、各种性质错综复杂，且大多数都很抽象。因此，在每次学完一部分知识的时候，有效地梳理知识是很有必要的，课前课后都需要思考巩固，这就需要我们充分发挥工匠精神中的劳动精神；高数作为一切理科的基本学习工具，学好高数能有效提高学术水平，为技术进步添砖加瓦，体现了工匠精神中对职业的奉献精神；对于数学问题的分析，需要严谨的逻辑，这反映出工匠精神中一丝不苟、精益求精的精神；工匠精神的核心要素是创新精神，众所周知，学习高数只靠死记硬背是行不通的，灵活变通地利用公式解决问题才是有效的学习方法，这个过程有利于提高我们的创新水平。从本质与核心理解高数要求学习者具有细心、耐心、专注、持之以恒的品质，这与工匠精神的内涵正相吻合。

（四） 人文情怀

“人文”指人类普遍的共性，指人类社会间交往所表现的基本道德，例如对人友善、待人真诚、尊重他人价值观等等。《辞海》中这样写道：“人文指人类社会的各种文化现象”，不同国家经过历史的沉淀诞生了不同的文化，培养学生的人文情怀，要求学生在学术研究与探索的道路上求同存异，保持高尚的情怀与学术操守。由于高等数学课程逻辑性强，理论公式繁多，与其他公共基础课程相比内容更加抽象，加之不同学生的学习能力、敏锐力有所差异，导致部分vrK5HRggNabVgNEXwcBznA==同学学习高数产生畏难情绪，学习的过程中又不善于向老师请教，由此，通过学生之间的交流既能促进高数的学习又能加强学生之间的人文情感，激发学生的人文情怀，对接学校培养方案。

二 实践案例

整个高数课程主要知识点可大致概括为微分和积分，以下将从这两方面探究其包含的思政教育。

（一） 在导数中引入家国情怀与工匠精神

在讲解导数的概念之前，我们可以先引入“高铁”这一话题，首先，通过图1让学生身临其境地感受到高铁背后所展现的大国工匠精神与新中国科技的强大，同时介绍高铁是中国“新四大发明”之一，是新时代劳动者智慧的结晶，一百多年来，一代代铁路人把民族精神和科学精神高度融合，在铁路设计、建造、养护、维修过程中凝练出的以“敬业坚守、追求卓越、精益求精、严谨专注”为主要内涵的工匠精神，并不断传承和弘扬，中国铁路才实现了从无到有、从弱变强的转变[5]；成为新时代美丽中国一道靓丽的风景线，为深入实施区域重大战略和区域协调战略提供了有力支撑[6]。通过这样的引入既可以激发学生的好奇心，增强民族自豪感，根植学生心中的家国情怀，传承发扬工匠精神，又可以引出接下来的问题：目前我国高铁的平均时速是多少？瞬时速度是多少？让同学们思考平均速度与瞬时速度的关系，并由此引入导数的概念：函数y=f（x）的自变量x在某点x0上有一个增量Δx，如果函数输出值增量Δy与自变量增量Δx的比值在Δx→0时的极限存在，则该极限为函数在点x0处的导数，记作f ′（x0）或|x=x0。导数是函数的局部性质，函数在某一点的导数描述了函数该点附近的变化率，若函数自变量和取值均为实数，则函数在某点导数就是该函数所对应的曲线在该点上的切线斜率。同时，函数的单调性、极值和最值等概念与函数的导数有着密切关系，学好导数可以为学习后续知识打下坚实的基础。

接着引出，在运动学中，物体的位移对于时间的导数就是物体的瞬时速度。由于导数的本质是通过极限的概念对函数进行局部的线性逼近，因此对于高铁而言，当平均速度的时间取值趋近于零时，则平均速度近似代表瞬时速度。接下来就可以深入介绍课程内容，在讲授完知识点后，还可以让学生们思考导数在生活中其他的应用，例如经济学中的边际问题、利润问题；变速运动有关问题；计算不规则体的面积、体积；工程造价方面的问题等。这种通过结合导数的定义引入思政元素，利用现实案例提高学生学习数学积极性的教学模式打破了传统教学方法，达到了思政教育与高数教学的高效融合。

（二） 在积分中引入中华优秀传统文化、人文情怀与哲学思维

课前，首先引用诗词典籍“不积跬步无以至千里，不积小流无以成江河”“众人拾柴火焰高”“学如逆水行舟，不进则退”等，让学生粗略地领悟积分的概念，通过古诗词的引入可以提升文化自信，有利于传承中华优秀文化。此外，古代河流两岸的土地划分问题，不规则物体面积体积测绘问题等，促使了定积分概念的产生，让我们体会到高等数学作为基础学科在生活中的广泛应用。

接着引入积分定义，介绍微积分产生的背景与发展历程。微积分思想在古代中国早有萌芽，例如公元前7世纪老子与庄子哲学中无限可分性和极限的思想；公元前4世纪《墨经》中有穷、无穷、无限小、无穷大的定义与极限、瞬时等概念；祖冲之计算圆周率是用正多边形逼近圆，运用了极限思想；三国时期的刘徽对积分学的思想主要有两点：割圆术及求体积问题的设想，其极限思想和无穷小方法，是世界古代极限思想的深刻体现。从微积分产生的背景、发展的历史以及研究方法的介绍中，可以潜移默化地培养学生的科学文化修养、家国情怀、人文情怀、文化传承、文化自信，开拓国际视野，树立正确的科学发展观与世界观[7]。

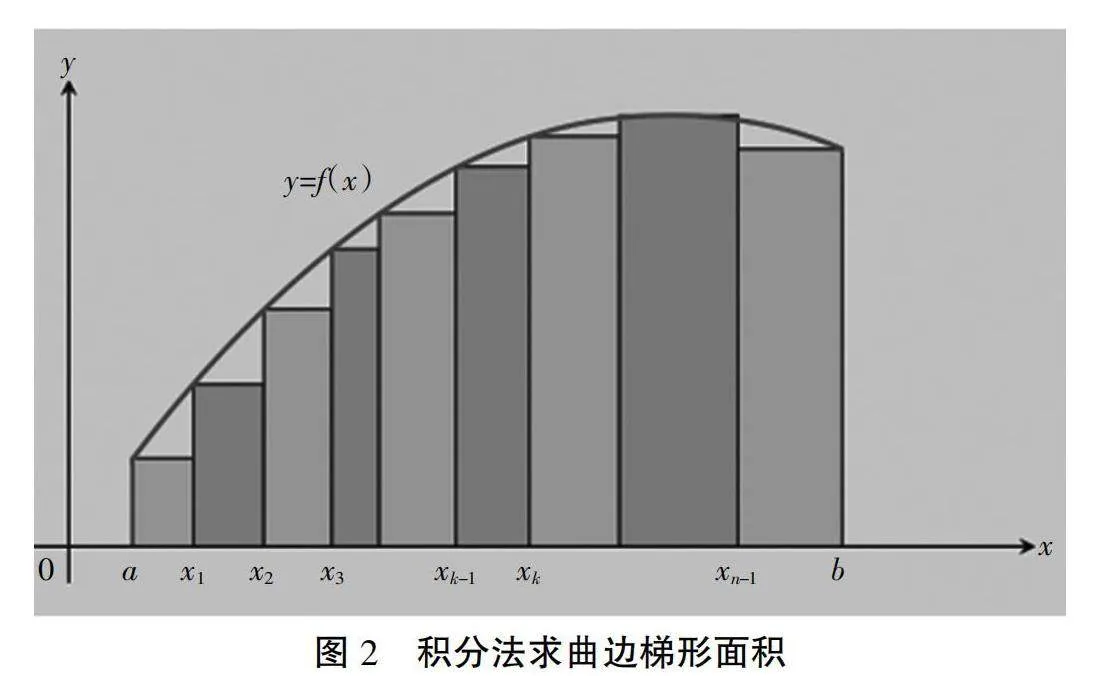
同时，唯物辩证法认为，矛盾是事物发展的动力，在整个数学的发展史上，伴随着许多大大小小的矛盾，正是这些矛盾给数学的发展带来了进步的源泉，微积分的发展过程中也充满着矛盾，例如连续与间断、有穷与无穷、微分与积分等，这些数学概念的在定义上就是相互矛盾的，整个数学发展史就是矛盾斗争的历史，正是这些矛盾不断完善着数学这个庞大的学科体系。如图2所示，将曲边梯形分割成若干个小曲边梯形，用小直边矩形近似替代小曲边梯形，各小矩形的面积之和的极限为曲边梯形面积，即“以直代曲”，而“曲”与“直”本身就是相互矛盾的对立关系，然而，通过积Kojsep2RCgJwMqoVsgxSgA==分的引入将其和谐地统一起来，实现两者的相互依赖与相互转化。

通过在授课过程中引入矛盾，可以促进学生数学思维的交流与碰撞，让学生从多个层面、多个方面、多个角度分析思考同一个问题，这样有利于学生从源头理解知识，培养学生多角度、多立场思考问题，用辩证的思维看待问题、发展的眼光解决问题的能力，从而达到锻炼学生发展哲学思辨能力的思政目标。

图2 积分法求曲边梯形面积

三 教学手段

（一） 调整教学大纲

教师在备课时，需要找准思政内容的切入点，并用恰当的方式顺其自然地切入到高数知识中。课件中可以将中华优秀古诗词、典籍文化、红色文化等作为引言引入课程知识点，如诗人王维《使至塞上》的“大漠孤烟直，长河落日圆”为我们展现了平面上的垂直空间关系（孤烟和大漠），以及圆与地平线从相离、相切到相交的空间位置变化，由此可引入高数中向量与空间几何的知识点；又如苏轼《赤壁赋》中“盖将自其变者而观之，则天地曾不能以一瞬；自其不变者而观之，则物与我皆无尽也，而又何羡乎！”体现了数学中变与不变的问题。在高等数学中不乏一些较为抽象的概念性知识或者形式不容易理解的复杂公式，通过实际使用才能体现其重要意义。因此在教学中要多增加各种公式定理的实际用例讲解，例如穿插考研经典例题、数学建模实例等，让学生能够直接学到数学公式定理的实际应用方式，在应用中形成更有效的理解和记忆。只有将数学教学与现实生活有机联系在一起，学生才不会感到陌生，同时也清晰地认识到学习数学的重要性。对于应用型大学而言，高等数学的教学还需要有一定的特色和针对性，保证学生更好地从高中的通识教育过渡到大学的专业性教育、职业性教育中，做到满足应用型大学的教育理念。

（二） 修改考核标准

将学生的思政素质考核纳入作业占比成绩中，通过思政学习，可以填补其他模块的分数空缺。作业考核具体包括：线上思政视频学习、参加各项与数学相关的竞赛、加入与高等数学课程相关的实践社团活动（如数学建模与算法学会、工程实践与创新能力工作室）等。以此培养起学生的学习兴趣和热情。目前大部分高校都对高等数学采取“大课”教学的方式，所有专业都在一起上课，参加相同的考试。但对于不同专业的学生，数学能力要求的偏向可能不同，例如对于计算机专业的学生，可以在考核中弱化对于概念记忆和公式推导的考察，而增加将数学知识活用到代码编写中的考察[8]。

（三） 高数与学生活动对接

鼓励学生成立数学相关的社团，如学校现有的数学算法协会、数模协会。鼓励学生参加高数相关的竞赛，如全国大学生数学建模竞赛、美国大学生数学建模竞赛、全国大学生数学竞赛等，这些竞赛着重强调研究问题和解决方案的原创性、团队合作、交流以及结果的合理性。有利于激发学生上进心，提高学习高数积极性。此外，学校可以增加建立数学学术交流会的次数，积极鼓励学生参与交流，不同观点相互讨论，剔除学生恐惧心理，提高学习的自信心，促进对数学的思考创新。

（四） 课后答疑与教学反馈

课堂时间有限，当学生跟不上课程进度时可以参与课后答疑，课后答疑的方式拓宽了学习高数的方式，使学生在课堂之外也可以向老师求助学习，这有利于学生养成勤学好问、善于思考的学习品质；同时，每章知识结束后通过问卷进行调查，问卷内容大致包括：对本章知识的理解程度（打分范围从1分至10分）、不理解的具体知识模块（列出本章各类知识点）等等，通过问卷及时反馈教学成果，便于老师调整改进。数学本身还是一个需要大量练习的学科，与高中相比，大部分高校的高等数学教学过程中都存在练习量不足的问题，另外，从反馈中可以发现，学生之间较难避免作业抄袭的问题。对于有能力的高校而言，最好的方式是整合现有资源建立一个线上习题库，课后作业转变为给每位学生布置某个章节的随机习题进行练习，最大程度地避免抄袭作业的问题，并且方便优秀的学生进行自主练习，实现自我提高。

四 结束语

1977年底恢复高考至今，我国教育事业蓬勃发展，时代的进步要求对于人才的培养已不能仅限于单方面的提升某种专业能力，而是培养出身心健康、德才兼备的内外兼修型人才，解决好培养什么人、怎样培养人、为谁培养人这个根本问题。因此，高校教育要坚持把立德树人作为中心环节，把思想政治工作贯穿教育教学全过程，实现全程育人、全方位育人[9]。高等数学在自然科学领域所发挥的基础作用已为世人所公认，在高等数学的教学过程中将思政元素作为一种正能量、源动力，及时、精准地融入到高等数学的教学体系中，注入学生的思想中，可以实现教书育人的有机统一。此外，高校高等数学课程思政体系建设更是践行立德树人根本任务的有效途径，应用型本科教育对于满足中国社会经济发展，对接高层次应用型人才需要以及推进中国高等教育大众化进程起到了积极的促进作用。通过将思政教育与高等数学教育的有机结合，能够培养和提升青年学生的工匠精神和人文情怀，助力学生全面发展，培养当代青年勇于投身国家建设、乐于奉献、为中华民族伟大复兴而不断奋斗、在中国式现代化进程中贡献自我的大国工匠品质。

参考文献：

[1] 深圳技术大学[J].中国高校科技，2019，373（9）：2，117-118.

[2] 蒋俊香，冯明佳.应用型大学专业课“机械制造技术基础”课程思政教学改革[J].轻工科技，2022，38（4）：85-87.

[3] 陈广福.应用型大学信号与系统课程教学改革与探索[J].电脑知识与技术，2022，18（24）：140-142.

[4] 王慧书.远程教育中《高等数学基础》课程思政实践探索[J].山西广播电视大学学报，2019（2）：29-32.

[5] 孙生会，纪海坡.传承工匠精神建好智能铁路[J].思想政治工作研究，2019，418（1）：41-43.

[6] 李乐诗.从绿皮火车到遍地高铁，铁路铺就中国画卷[J].科学之友，2023（3）：42-43.

[7] 刘大莲，曹彩霞，刘佳，等.高等数学课程思政探索及经典案例分析[J].北京联合大学学报，2021，35（3）：34-38.

[8] 司秀林.应用型大学高等数学课程教学改革思考[J].黑龙江科学，2019，10（17）：74-75.

[9] 习近平在全国高校思想政治工作会议上强调：把思想政治工作贯穿教育教学全过程，开创我国高等教育事业发展新局面[N].人民日报，2016-12-19.