借助数学史和信息技术展现统计方法的合理性

摘 要：在基础教育阶段中，数学教学更多是对数学知识形成合理化的解释，这在统计方法的教学中更为明显.数学史和信息技术分别从统计方法的来源与用途两个角度对统计方法进行合理化解释.本文以苏教版《普通高中教科书数学选择性必修第二册》中“变量的相关性”为例，借助数学史和信息技术对教学过程进行重构，使得学生在对比函数、回顾历史、构建指标的过程中逐步理解相关性以及感受相关系数的合理性.

关键词：统计方法；合理性；数学史；信息技术

与高等教育阶段不同，基础教育阶段的数学教学更多是要为数学知识找到合理的解释，也就是利用一些局部的证明或者直观的感受来说明数学知识的合理性.对于统计部分的内容来说，统计方法描述的对象是数据，并非直接指向现实世界，这就造成了学生在一定程度上难以获得直观的感受.由于学生前置知识的缺失，使得演绎证明难以符合实际教学.即使能够进行演绎证明，教师选择采用归纳的直观方式呈现统计方法会更有利于学生接受统计知识.因此，教师需要思考通过何种教学方式来展现统计方法的合理性.

1 展现统计方法合理性的教学方式思考

1.1 借助数学史实展现统计方法来源的合理性

数学史与数学教育（HPM）以历史发生原理和再创造理论为基础，强调学生在数学知识的认知过程中遵循历史过程，体会知识的创造过程，并在已有知识的基础上融入自己对知识的理解，进行再创造.融入数学史的教学需要教师追溯数学知识的源头，并渐进式地呈现数学历史的发生过程，从而使得学生可以结合自己的学习情况，进行数学化的分析与反思.

对统计方法来源的阐释是统计教学中的重要一环，其本质是对促使统计方法产生的根本问题进行溯源.由此，教师可以帮助学生了解统计方法产生的缘由以及过程，明确统计方法建构的目的，从而解决学生对于方法来源的疑问，加深学生对于统计方法的认识.教师将数学史融入统计教学不仅能够回溯统计方法诞生的源头，还能发掘统计方法建构的过程，从而站在统计方法构建思路的视角，帮助学生渐进式体验统计方法产生的过程，深刻感受统计方法来源的合理性.

1.2 借助信息技术展现统计方法用途的合理性

随着信息技术的发展，其对数学教学的影响越来越大.《普通高中数学课程标准（2017年版2020年修订）》在“教学建议”中就明确指出：“教师应注重信息技术与数学课程的深度融合，实现传统教学手段难以达到的效果.”［1］教师通过对信息技术的合理使用，可以设计出生动的数学教学活动，呈现新型的数学教学方式方法，为学生提供丰富数学学习资源.

信息技术和统计教学之间有着密不可分的联系.在统计中不仅有大量的数据需要用到信息技术工具进行分析，信息技术也能够用于验证统计方法用途的合理性.通常情况下对于方法合理性的验证往往依赖行动试验和思维试验两种方式，即在具体的行动或者思维过程中验证方法用途的合理性.信息技术的使用在一定程度上可以代替行动试验，其通过大量计算以及图象绘制的方式呈现统计结果，来帮助学生获得对于统计方法的直观感受.这不仅较大程度上缩减了试验方法合理性消耗的时间，还使得学生能够在短时间内明确统计方法用途的合理性.

2 展现统计知识合理性的教学实践示例 本文以苏教版《普通高中教科书数学选择性必修第二册》中“变量的相关性”的教学为例，在分析教材、学情、教学重难点的基础上，尝试将数学史和信息技术融入统计教学实践之中.

2.1 教材分析

“变量的相关性”是线性回归分析的第一课时，故在进行教学内容分析时教师需要从线性回归这一整节课的角度考虑.线性回归分析这一节的内容大致为用散点图直观上描述变量间是否具有统计相关性，到用相关系数刻画线性相关关系的密切程度，再到建立一元线性回归模型进行预测.教学经历了由定性分析到定量分析线性回归的可行性，以及实施线性回归的过程.变量的相关性与一元回归模型紧密联系，都是研究两个数值型变量间的相关关系，只有通过相关系数判断出两个变量之间具有较强的线性关系时，建立一元回归模型才有意义.

聚焦到“变量的相关性”这一课时.教材首先明确了两个变量之间的数量关系有两种不同的类型：一种是函数关系；另一种是相关关系.在这之后，教材中又指出变量间的相关关系可作如下直观描述：当一个变量取一定的数值时，与之对应的另一个变量的值虽然不完全确定，但它按某种规律在一定的范围内变化.在定性描述变量间的相关关系尤其是线性相关关系之后，则通过定量手段描述变量间的相关关系程度.教材直接构建了相关系数，并对相关系数如此构建的合理性进行了简要的描述，并在此基础上给出了相关系数的性质.

笔者比较苏教版教材和人教版教材，发现两版教材对于知识设置的顺序是基本一致的，但在构建相关系数公式的部分有一定的差异.在严谨性上，两版教材都有所缺失，当然也是由于高中缺少相关前置知识的学习.在直观性上，苏教版的直观性较好，可以更好地进行数形结合；人教版的构建方式也可以有直观性的解释，但并未体现在教材中.

2.2 学情及教学重难点分析

必修课程的学习使学生已经初步建立样本估计总体的思想，为学生理解用样本相关系数推断变量间的相关性，以及估计回归系数奠定了认知基础.刻画数据特征（均值、方差）的一般方法，为构造样本相关系数提供了可以借鉴的思想方法.

对于“变量的相关性”这一课时来说，理解两个随机变量的相关性可以通过成对样本数据进行分析，故线性相关关系与相关系数的概念与运用是教学的重点.相关系数公式的建立是教学中较为困难的部分，学生常常难以理解，故对于相关系数公式的理解是教学的难点.

2.3 借助数学史和信息技术的教学实践

教学环节1：对比函数，提出问题.

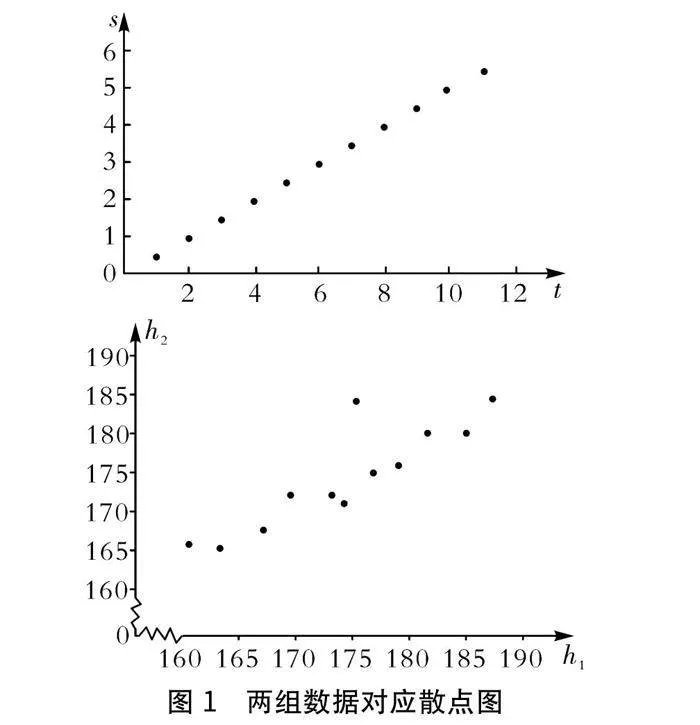
活动1：有两组数据；第一组数据是由物理学家在研究匀速运动时收集到的；第二组数据是由生物学家在研究性状遗传时收集到的.两组数据对应散点图如图1所示.

问题1 观察第一组数据，在匀速行走时，时间t（单位：秒）和距离s（单位：米）有什么关系.你会用什么数学工具来描述它们之间的关系.

问题2 观察第二组数据，父代身高h1（单位：厘米）和子代身高h2（单位：厘米）之间有什么关系.你想用什么数学工具来描述它们之间的关系.

【设计意图】在数学史上，线性回归的研究引发了对相关性以及相关系数的思考.线性回归和一次函数之间有着很多联系，一次函数可以用来反映变量间线性的函数关系，线性回归可以用来反映变量间线性的相关关系.教师可以通过带领学生对比函数关系，来研究变量的相关性.教师设置活动1的两个实例引导学生通过仔细观察、深入思考、主动表达，提升学生的参与度和学习兴趣；通过学生的描述导出“函数关系”和“相关关系”的定义，并从直观比较中获得对“函数关系”和“相关关系”的感性认识；对比“函数关系”，启发学生思考利用直线描述相关关系，学会利用确定性工具解决不确定性问题的思想方法.通过对比函数关系引出变量相关性的背景知识和后续的探索，它起到了统领整个变量相关性学习的作用.

教学环节2：回顾历史，寻找答案.

活动2：回顾数学史，介绍英国科学家高尔顿（Francis Galton）曾利用直线描述父代身高和子代身高的变化趋势.［2］教师进一步给出线性相关关系以及线性回归分析的定义.线性回归中“回归”取自向中心回归之意.例如，高个子的后代平均来说也高一些，但不如亲代那么高，要向平均身高的方向“回归”一些.教师结合实例解释并强调均值点和线性回归线之间的联系.

【设计意图】教师增添数学史的内容，介绍高尔顿及其研究，有利于学生对于科学家故事的了解，使得学生对于接下来的学习产生一定的兴趣；指出使用一次函数反应变量间的相关关系有一定的合理性，进而引出线性相关关系的概念；对“回归”的介绍，强调平均值点的重要性，为使用平均值点构建相关系数提供支持.

教学环节3：判断程度，构建指标.［3］

活动3：观察如下散点图（如图2）中点的变化趋势，思考如下问题.

问题1 是否所有的散点图中的点的变化趋势都可以用直线描述.请结合前两张散点图先说一说.如果你觉得可以用直线描述，请在图中画一画.

问题2 图（3）中的情况能不能用直线描绘，或者说用直线描绘的合理程度如何，用斜率正的还是斜率负的直线描述，具体斜率如何.如果你觉得可以用直线描述，请在图中画一画.

【设计意图】教师在分析图（1）和图（2）时，引出“正相关”和“负相关”的概念.通过引导学生动手实际操作以及与师生间的交流，使学生理解统计学虽然使用数理工具但更侧重于强调合理性.图（1）和图（2）利用直线描述相关关系的合理程度高；对于图（3）各个学生就会有不同的看法，合理性就相对弱一些.教师通过对图（1）、图（2）以及图（3）中绘制出的直线进行比较，引出相关性指标的名称相关系数.教师还需引导学生发现绘制的直线大致都会经过平均值点，明确平均值点对于相关系数构建的重要作用.

教学预设：教师允许学生自主绘制各种直线，但需要保证图（1）中直线斜率为正，图（2）中直线斜率为负.对于图（3）的讨论，学生可以畅所欲言，然后教师通过提问，引导学生阐述自己想法的合理性，以及评价他人想法的合理性，营造出各人想法的合理程度难以确定的情境，从而引出相关系数的内容.同时，教师还需要抓住学生所绘直线中的共性，即大致都经过了平均值点，引出利用平均值点构建相关系数的想法.

活动4：建立相关系数公式.

设置疑问：该怎么用平均值点和其他点说明利用直线描绘变化趋势的合理程度.

分类讨论如下.

（1）只有两个数据点时，用过此两点的直线描述变化趋势显然合理，不予讨论.

（2）三个数据点共线时，构造相关系数公式.

记三个点分别为A，B，C，平均值点为P.记A（x1，y1），B（x2，y2），C（x3，y3），Px ，y .

由于点A，B，C，P共线，则有kAP=kBP=kCP=

λ，从而有y1-=λx1-，

y2-=λx2-，

y3-=λx3-.

构造向量a与b，a=x1-，x2-，x3-，b=y1-，y2-，y3-，并记＜a，b＞=θ，则有

cosθ=3i=1xi- yi- 3i=1xi- 23i=1yi- 2，并将这个值称为相关系数r.

（3）在三点不共线时，仍使用此公式计算相关系数.

（4）将此公式推广，获得n个点的相关系数公式r=ni=1xi- yi- ni=1xi- 2ni=1yi- 2.

【设计意图】教师通过三点共线的情况建立出相关系数公式，并进一步归纳出三点不共线以及n个点时的相关系数公式，帮助学生理解相关系数公式.

活动5：考查相关系数公式的合理性.

设置疑问：相关系数公式是在点到平均值构成直线的斜率一致时得出的，那么斜率不一致时是否也能够描述相关程度.

绘制图象：一是绘制相关系数r=cosθ的图象，其中θ∈［0，π］；二是绘制给定具体相关系数的散点图.

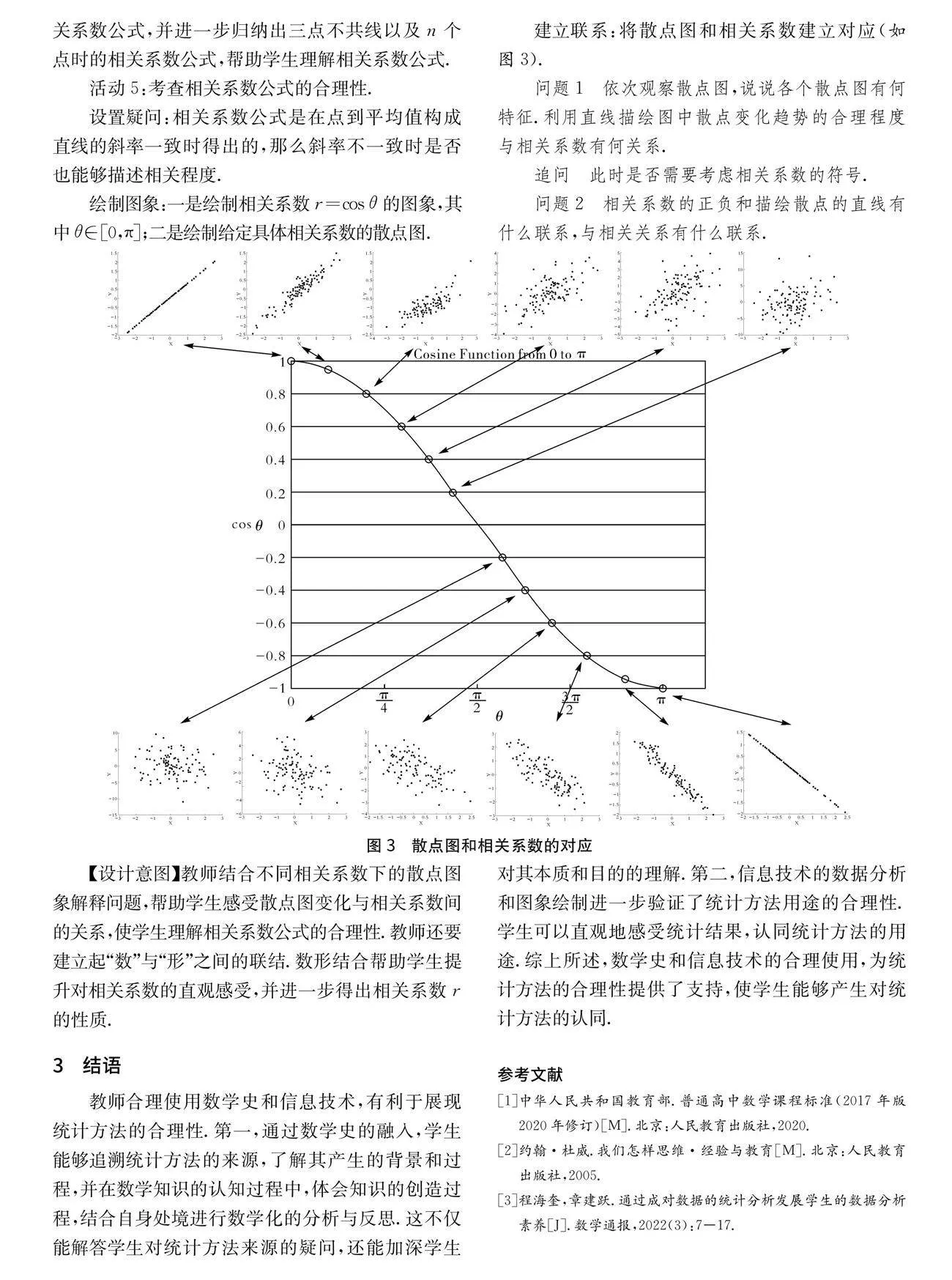
建立联系：将散点图和相关系数建立对应（如图3）.

问题1 依次观察散点图，说说各个散点图有何特征.利用直线描绘图中散点变化趋势的合理程度与相关系数有何关系.

追问 此时是否需要考虑相关系数的符号.

问题2 相关系数的正负和描绘散点的直线有什么联系，与相关关系有什么联系.

【设计意图】教师结合不同相关系数下的散点图象解释问题，帮助学生感受散点图变化与相关系数间的关系，使学生理解相关系数公式的合理性.教师还要建立起“数”与“形”之间的联结.数形结合帮助学生提升对相关系数的直观感受，并进一步得出相关系数r的性质.

3 结语

教师合理使用数学史和信息技术，有利于展现统计方法的合理性.第一，通过数学史的融入，学生能够追溯统计方法的来源，了解其产生的背景和过程，并在数学知识的认知过程中，体会知识的创造过程，结合自身处境进行数学化的分析与反思.这不仅能解答学生对统计方法来源的疑问，还能加深学生对其本质和目的的理解.第二，信息技术的数据分析和图象绘制进一步验证了统计方法用途的合理性.学生可以直观地感受统计结果，认同统计方法的用途.综上所述，数学史和信息技术的合理使用，为统计方法的合理性提供了支持，使学生能够产生对统计方法的认同.

参考文献

［1］中华人民共和国教育部.普通高中数学课程标准（2017年版2020年修订）［M］.北京：人民教育出版社，2020.

［2］约翰·杜威.我们怎样思维·经验与教育［M］.北京：人民教育出版社，2005.

［3］程海奎，章建跃.通过成对数据的统计分析发展学生的数据分析素养［J］.数学通报，2022（3）：7-17.