Reissner能量方程视角下的改进Timoshenko梁动力学方程及其在轴力识别中的应用

摘要： 在轴力识别中，动力测试法建立在杆件振动理论的基础上，因此杆件的振动方程决定了轴力识别的结果。为提高杆件轴力识别的精度，从能量角度出发，推导出轴力作用下Timoshenko梁的自由振动方程。引入缩聚假设，建立了Timoshenko梁关于位移、应力和轴力的Ressiner能量方程；使用极值定理，求得平面梁的运动和应力的平衡方程，化简上述平衡方程得到轴力作用下Timoshenko梁自由振动的方程，发现与经典结构动力学方程相比，所提出的方程多出与轴力和剪切效应有关的两项。使用本文推导的方程分别从数值模拟和试验研究两个方面对杆件进行轴力识别，发现与传统的识别方法相比精度有较大的提高，验证了其正确性和适用性。

关键词： Timoshenko梁； 自由振动； 模态分析； 轴力识别

中图分类号： O327 文献标志码： A 文章编号： 1004-4523（2024）10-1723-08

DOI：10.16385/j.cnki.issn.1004-4523.2024.10.010

引 言

杆件具有形式简单、受力明确和易组装等优点，因此被广泛应用在工程结构中，如网壳结构、网架结构和斜拉桥等。然而在这些结构服役期间，复杂多变的荷载可能会导致关键杆件受力超出设计范围，进而引起结构损伤甚至倒塌。因此，如何在正常工作状态下，高效、准确地检测关键杆件所受轴力的变化，对结构主体的健康监测起着至关重要的作用［1］。

目前为止，杆件轴力识别方法按识别机理可以分为：光纤光栅法［2‑3］、磁通量法［4‑5］、波动法［6‑7］和动力测试法［8‑10］等。其中，动力测试法以方便、快捷、经济和精度高等优点被广泛使用。其主要机理是根据轴力识别的特征方程，利用杆件的振动信息（如频率和振型）进行轴力识别。而轴力识别的特征方程是在杆件振动理论的基础上建立的，因此，使用不同的振动理论，杆件轴力识别的结果将产生明显差异。

起初动力测试法使用弦振动理论，在已知边界条件下通过建立固有频率与轴力的关系来识别杆件的轴力［11］。虽然弦理论对柔性细长杆的轴力有良好的识别效果，但由于该理论没有考虑杆件的弯曲刚度，所以对考虑弯曲变形的杆件轴力的识别效果较差。为了提高考虑弯曲变形的杆件轴力识别的精度，学者首先以Bernoulli‑Euler梁理论为基础，建立轴力识别的特征方程。例如，LI等［12‑13］在考虑轴力影响的Bernoulli‑Euler梁的基础上，提出了未知边界条件下杆件轴力的识别方法。LAGOMARSINO等［14］将杆件简化为Bernoulli‑Euler梁，采用前3阶固有频率对杆件进行轴力识别。然而研究发现Bernoulli‑Euler梁理论只能提高对细长杆件轴力的识别精度，对于受剪切变形和转动惯量影响较大的短杆而言，Bernoulli‑Euler梁的识别误差不可忽略。针对这一问题，学者们开始将Timoshenko梁理论应用在杆件轴力识别的问题中，这是因为Timoshenko梁能够同时考虑弯曲引起的转动惯量和剪切变形影响，可以更好地模拟短杆的振动情况。AMABILI等［15］使用经典Timoshenko梁理论模拟实际杆件，提出了一种基于频率的轴力识别方法。袁永强等［16］采用修正的Timoshenko梁理论，同时考虑传感器质量的影响，提出了一种改进的轴力识别方法。李东升等［17‑19］基于修正的Timoshenko梁理论，分别对不同截面和不确定刚度的杆件进行轴力识别。

在上述研究中，梁的振动方程都是根据力的平衡方程建立的。而本文将采用一种新的推导方法，充分考虑轴力对Timoshenko梁的动力特性的影响。具体过程如下：在GUYADER［20］研究基础上，从Ressiner能量方程出发，利用极值定理，推导出轴力作用下Timoshenko梁自由振动的方程，并通过MATLAB数值模拟和杆件试验验证该方程的正确性和适用性。

1 轴力作用下Timoshenko梁振动方程的理论推导

轴力作用下经典Timoshenko梁的弯曲振动是从材料力学的角度，利用力和弯矩两个平衡方程得到的［21］。而本节将换个思路：从能量角度推导轴力作用下Timoshenko梁的弯曲振动方程。

1.1 基本公式

首先引入推导过程中所需的三个基本公式。

1.1.1 直梁位移和应力的缩聚假设

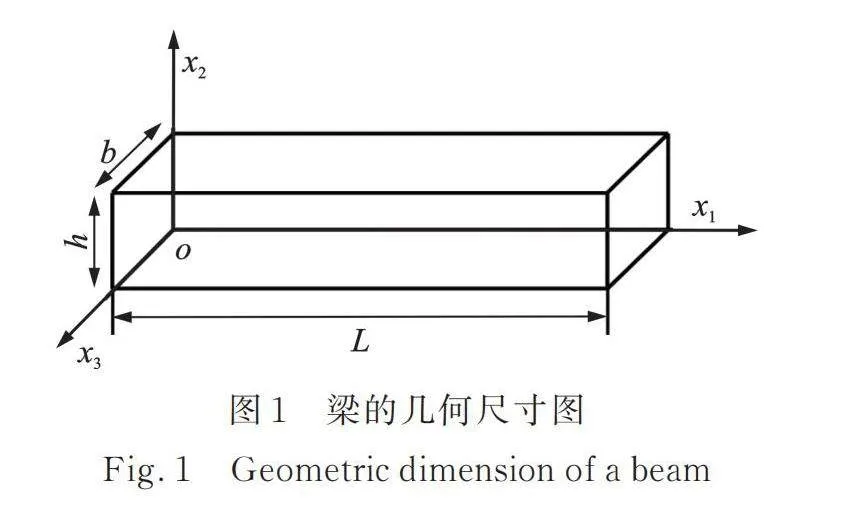
考虑如图1所示的三维直梁的几何模型。其中，宽度b和高度h两个维度方向上的尺寸比梁长L小，且轴线x1与梁的中心线重合。

将梁上任一点的位移和应力进行泰勒级数展开，其表达式为［20］：

（1）

（2）

式中 为空间梁上任意一点的位移；为空间梁上任意一点的应力。

由上式可知：梁上任意点的位移和应力与函数，和等有关。然而这些函数都是未知的，为了解决这一难题，下面将任意点的位移和应力的泰勒展开式进行改写，其表达式为：

（3）

（4）

式（3）和（4）与式（1）和（2）是完全等价的，只是将偏导数的形式改写成未知函数的表达式，此时未知函数，和等是相互独立的，且相互之间不存在联系。这样就把梁的三维问题转换为单维度问题，这种方法就称为缩聚假设。

1.1.2 Reissner能量方程

当梁的应力、外力和位移都已知时，可以用Reissner能量方程表示梁的总能量，其表达式为：

（5）

式中 R1为梁单元总能量；p为梁的密度；εij为应变；fi为体力；Fi为外力；V为梁单元的体积；为梁单元的外表面积；Sijkl为柔度系数；t0，t1分别表示任意两个时间段。

1.1.3 方程极值计算的定理

基于时间和位移的梁振动方程表达式如下所示：

（6）

令，，本文给出j=2时，关于上述泛函中w（x，t）的极值计算的定理为［22］：

（7）

1.2 公式详细推导

当平面梁发生弯曲振动时，将在轴1和2方向上分别产生横向位移和剪切位移，如图2和3所示。而梁的横向和剪切位移会引起正应力和剪应力的出现。弯曲振动的平面梁经过缩聚假设后位移和应力的表达式为：

位移：

（8）

应力：

（9）

由式（8）和（9）可知：对于平面梁而言，位移存在两个未知变量和，应力也有两个未知变量和。此时，平面梁的振动问题转化为求解上述四个未知数的问题。

为了求解上述四个未知变量，就必须建立四个未知变量之间的关系。因此，本文利用Reissner原理，建立了考虑轴力影响的四个未知变量的Timoshenko能量方程。

首先给出各向同性材料应力‑应变的关系为：

（10）

并由弹性力学相关知识，给出轴力N在平面梁上所做的功为：

（11）

然后，在已给条件下建立了关于轴力N和的Timoshenko梁的Reissner能量方程为：

（12）

转动惯量和面积的表达式为：

（13）

因此，方程（12）可以简写为：

（14）

随后，对方程（14）运用极值定理，求出关于轴力N和的等式方程为：

（15a）

（15b）

（15c）

（15d）

其中，方程15（a），（b）分别为沿1，2轴方向的运动方程；而15（c）和（d）为关于应力的平衡方程。

化解方程15（c）和（d），得到应力未知变量和与位移未知变量和的关系为：

（16a）

（16b）

将方程（16）代入方程15（a）和（b）中，得到只有位移未知变量和方程的表达式为：

（17）

最后，进一步将公式（17）两式联合整理可得：

（18）

由于，且将横向位移用w表示，再把x1替换成x表示，从而得到轴力作用下的Timoshenko梁的自由振动方程为：

（19）

通常，剪应力在梁横截面上均匀分布，因此需要引入剪切变形系数ky对G进行修正，其表达式为：

（20）

因此，轴力作用下经典Timoshenko梁的弯曲自由振动方程写为：

（21）

从式（21）中可以发现：与力的平衡方法［22］相比，本文推导的动力学方程前6项与力的平衡方法得到的结果完全相同，但还多出与轴力和剪切效应有关的后两项，即和 。

2 运动方程在杆件轴力识别中的应用

本节简略介绍一下使用本文推导的轴力作用下Timoshenko梁振动方程进行杆件轴力识别的过程，详细过程请参考文献［16］。

首先使用分离变量法求解式（21），并且假定平面梁的弯曲振动方程为：

（22）

式中 和分别表示平面梁的圆频率和相应的振型。

将式（22）代入式（21）中可得：

（23）

式中 a，b和c的表达式分别为：

（24）

由式（24）可知，与力的平衡方法相比，在轴力识别过程中，系数a多出一项，同时系数b也多出一项，而振型函数的通解为：

（25）

式中 系数只与边界条件有关；参数的详细表达式见文献［16］。

当杆件边界未知时，可以利用杆件上某一模态振型上的5个点处位移值，得到4个位移模态比，例如：

（26）

紧接着，对式mnT5ucJm+aSYuZ5kyamu8NSQseYXfNC213aDHCZOw/U=（26）进行变换，得到了关于4个待定参数C1，C2，C3，C4的联立方程：

（27）

式中 S的具体表达式详见参考文献［16］。由于待定参数Ci（i=1，2，3，4）作为杆件的边界条件，必有非零解。因此其系数矩阵S的行列式必为0，然后利用S的行列式为零这一性质，求得杆件真实轴力的大小。

3 数值算例分析

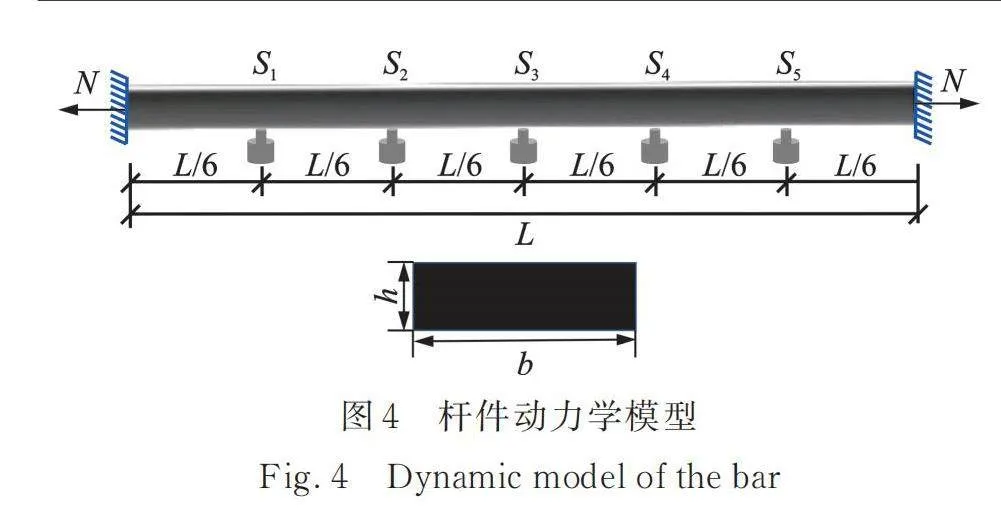
为了验证本文运动方程推导的正确性和轴力识别的适用性，本节使用文献［17］提出的改进Timoshenko平面梁单元，通过MATLAB软件建立与文献［13］相同的杆件动力学模型，如图4所示。图中S1～S5是杆件在长度方向上等距离布置的节点位置。杆件的结构参数如下：弹性模量 Pa，泊松比υ=0.3，密度p=7860 kg/m3，剪切变形系数ky=5/6，矩形截面的宽度和高度分别为b=0.035 m和h=0.005 m。杆件的边界条件为两端固支，并且两端受到轴向拉力N的作用。下面将从以下3个方面进行验证，并与文献［21］的动力学方程进行对比分析。

3.1 不同模态阶数

首先，以0.72 m长度的杆件作为研究对象，轴向拉力预设为15 kN。用MATLAB软件对轴力作用下的杆件进行模态分析，并提取了前5阶模态的固有频率和相应振型，详细数据如表1所示。然后，采用第2节的识别算法对矩形杆件进行轴力识别。随后，对不同模态阶数下的杆件进行轴力识别，详细的识别结果如表2所示。

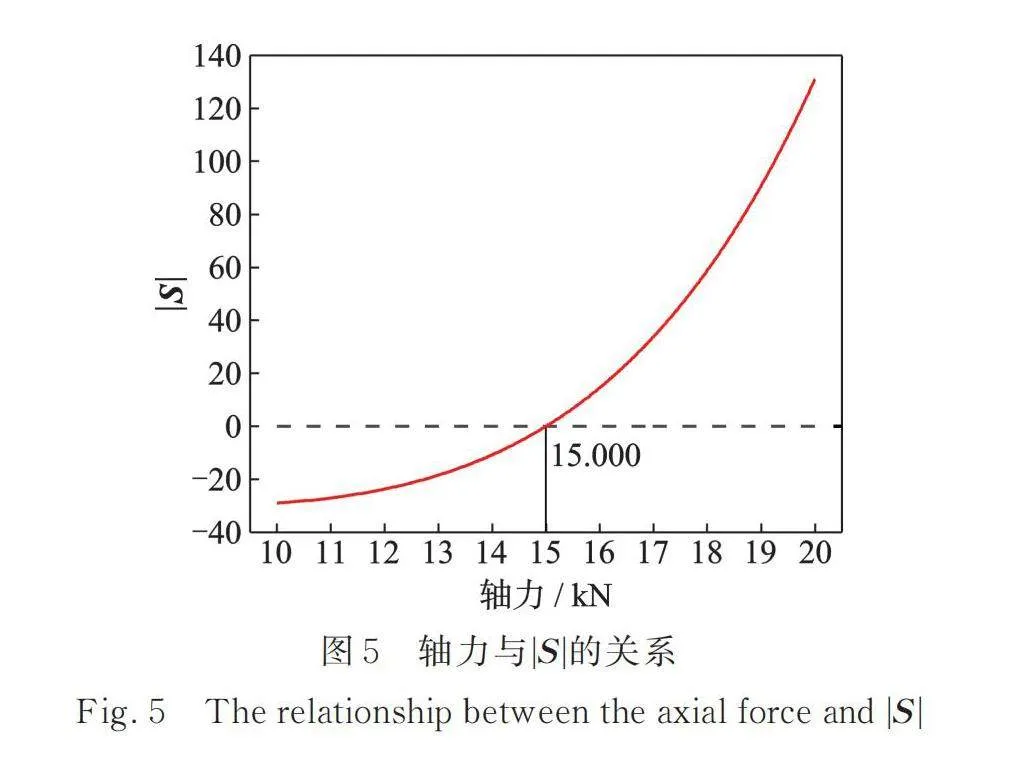
图5给出了第1阶模态下杆件轴力与之间的关系曲线，图中水平虚线表示为0。由图5可知：采用本文推导的动力学方程对杆件进行轴力识别时，识别结果为15.000 kN，误差为0%。证明了本文推导动力学方程的正确性；同时也说明该动学方程可用于杆件的轴力识别。

由表2可知，采用文献［21］中考虑轴力影响的Timoshenko梁动力学方程进行轴力识别时，任意阶模态都存在误差。当使用杆件的1阶模态信息进行轴力识别时，识别结果为15.004 kN，误差仅为0.027%。但随着模态阶数的增加，识别误差逐渐增大，当使用5阶模态信息进行轴力识别时，识别误差为0.347%。而在相同工况下，采用本文推导的轴力作用下Timoshenko梁自由振动方程进行轴力识别时，任何阶模态下轴力识别结果都为15.000 kN，识别误差为0.000%，证明了本文推导动力学方程的正确性和精确性。

3.2 不同轴力

本节将研究在不同轴力工况下，本文推导动力学方程对轴力识别结果的影响。同样以0.72 m长度的杆件作为研究对象。此时，轴向拉力5～25 kN逐步加载，步长为5 kN。提取了不同轴力工况下杆件的第3阶模态的固有频率和对应传感器位置上的振型数据，然后对不同轴力下的杆件进行轴力识别，识别结果如表3所示。

从表3中可以发现，采用文献［21］中动力学方程对不同轴力情况下的杆件进行识别时，其误差均小于0.5%，表明轴力大小对杆件识别结果影响较小。与此同时，采用本文的动力学方程在任何轴力工况下进行轴力识别时，其误差都为0.000%，说明本文的动力学方程对不同杆件轴力进行识别时都有非常高的识别精度。

3.3 不同杆件长度

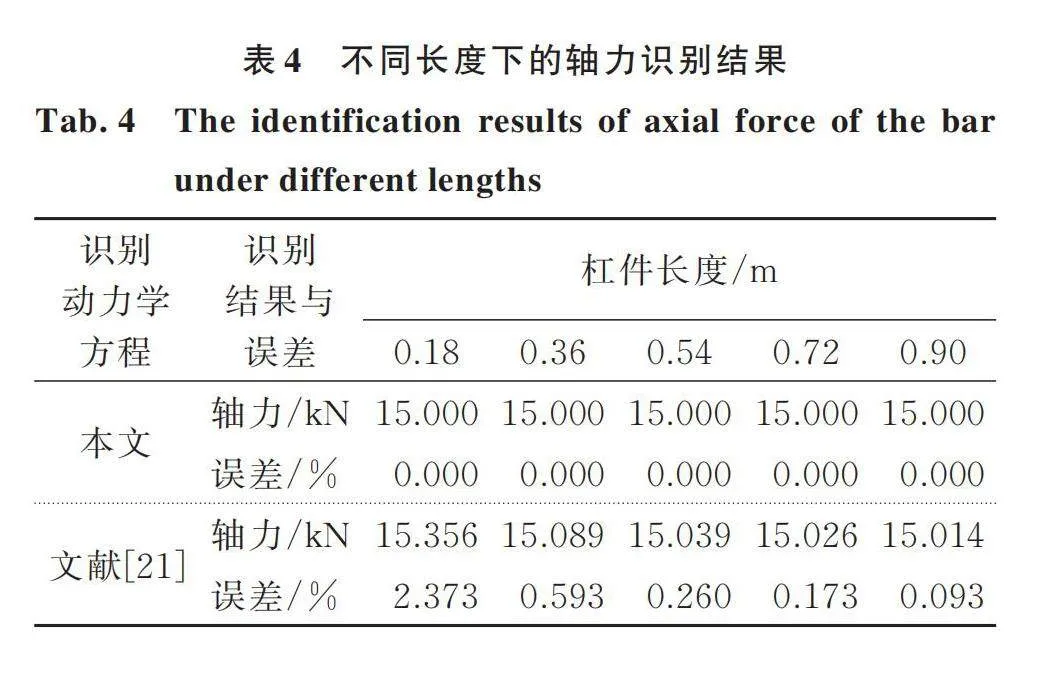
第1，2节以细长杆件作为研究对象，此时剪切变形对杆件动力学特性影响较小。为了验证本文推导的动力学方程对剪切变形影响较大的杆件依然适用，本节分析了不同长度的杆件对轴力识别结果的影响。杆件两端的轴向拉力为15 kN，杆件的长度分别为0.18，0.36，0.54，0.72和0.90 m。利用杆件的第3阶模态信息进行轴力识别，详细的识别结果如表4所示。

从表4中可以看出，文献［21］的运动方程随着杆件长度的减短，识别误差在不断增大。当L=0.90 m时，误差仅0.093%，而当L=0.18 m时，识别误差达到2.373%。而产生这种现象的原因是随着杆件长度的减短，剪切变形对杆件动力学特性影响显著。但对于本文提出的动力学方程而言，在任何长度下的识别结果都为15.000 kN，证明本文提出的动力学方程能更好地模拟剪切变形对杆件动力学特性的影响。

4 试验分析

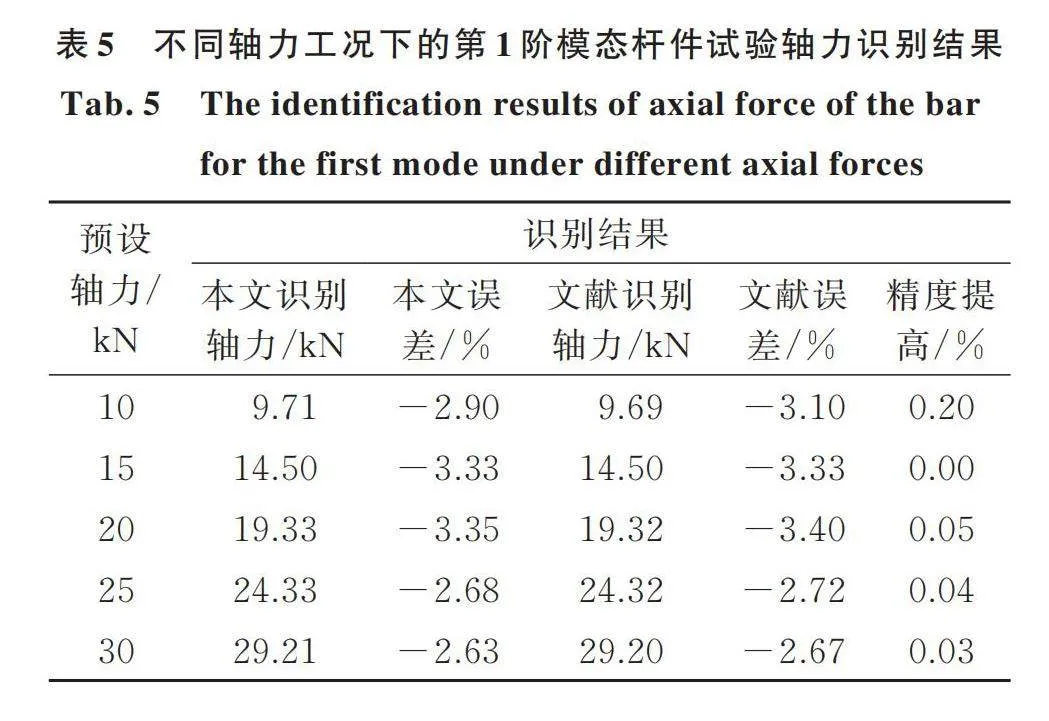
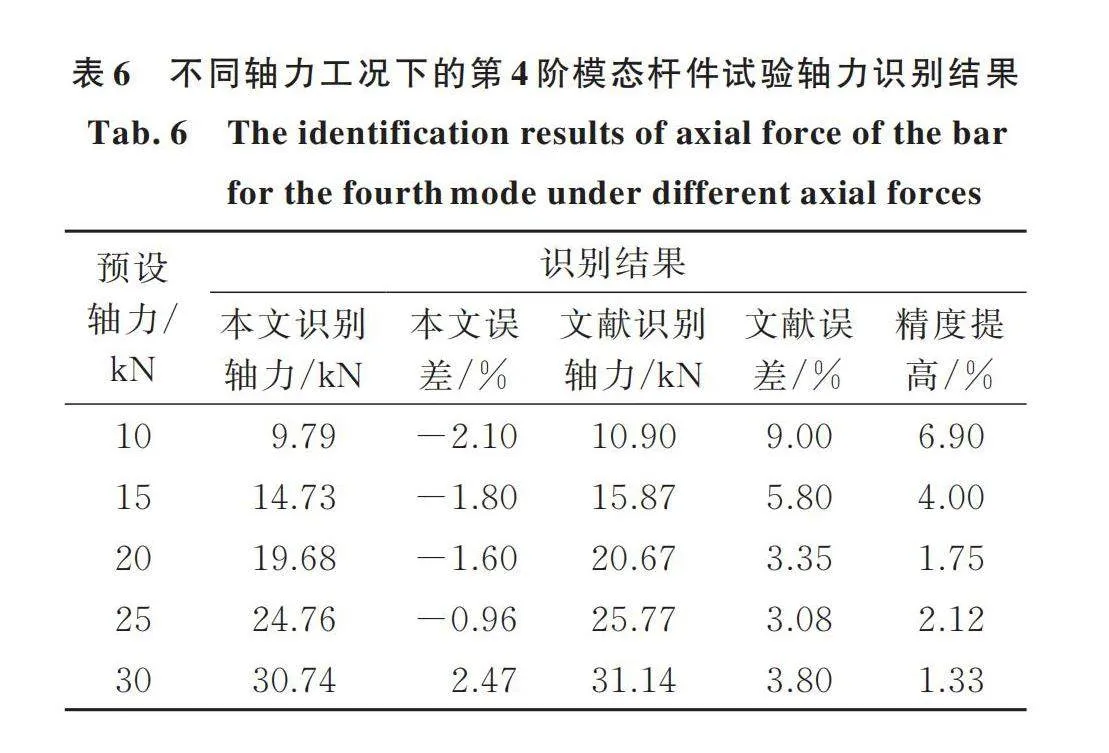
第3部分的数值分析证明本文提出的动力学方程的精确性，本节将再次通过试验方式进行验证。试验数据来自文献［13］，试验杆件的结构参数与数值分析的完全相同，其中梁长L=0.72 m。5个A353B66加速度传感器以等间距0.12 m布置在杆件上。动态激励方式为单点锤击，然后使用随机子空间方法对采集到的加速度数据进行分析得到矩形杆件在不同荷载阶段的前5阶自振频率和传感器归一化模态位移比信息，具体数据见参考文献［13］。通过对比可以发现：本文表1数值模拟数据与文献［13］的试验数据相吻合，也验证了数值模型的正确性。随后使用本文推导的动力学方程对试验杆件进行轴力识别，并与文献［13］的轴力识别结果进行对比。表5和6分别列出了第1阶模态和第4阶模态在不同荷载工况下杆件的轴力识别结果和相对误差。

从表中可知，对于第1阶模态，采用本文提出的Timoshenko梁的动力学方程与文献［13］中欧拉梁的识别结果相近，轴力识别精度最多提高0.20%。而对于第4阶模态，本文识别精度显著提高，其中在实际轴力为10 kN时，识别轴力达到9.79 kN，误差为-2.10%，识别精度提高了6.90%。出现这种现象的主要原因是：对于梁的振动而言，高阶模态的剪切影响不可忽略，因此采取本文推导的Timoshenko梁理论进行杆件识别时，具有更高的识别精度。上述试验结果表明了本文提出的动力学方程的正确性和在轴力识别中的适用性，且能够准确模拟实际杆件的振动情况。

5 结 论

本文从Reissner能量方程角度推导出轴力作用下的Timoshenko梁自由振动的方程，通过数值模拟和试验测试两个方面验证了该方程的正确性和在杆件轴力识别中的适用性，主要结论如下；

（1）与经典动力学方程相比，本文提出的改进Timoshenko梁动力学方程更好地考虑了剪切变形对轴向杆件振动特性的影响，因此在杆件轴力识别中具有更好的精度。并且为以后推导更为复杂的梁的运动方程提供了一种思路。

（2）与欧拉梁理论相比，本文提出的改进Timoshenko梁动力学方程在低阶模态下的轴力识别结果与欧拉梁的识别结果几乎相同。而随着模态阶数的增加，本文提出的动力学方程识别结果更好。

（3）数值模拟和试验都证明了本文推导的动力学方程能够用于杆件的轴力识别中，并且能够准确识别出不同工况下杆件的真实轴力。

参考文献：

［1］LI Hongnan，LI Dongsheng，REN Liang，et al. Structural health monitoring of innovative civil engineering structures in Mainland China［J］. Structural Monitoring and Maintenance，2016，3（1）： 1-32.

［2］李红明，张晓锋 ，唐军，等. 新型光纤光栅测量法在系杆拱桥索力监测中的应用［J］.江苏科技大学学报（自然科学版），2020，34（3）： 97-104.

LI Hongming，ZHANG Xiaofeng，TANG Jun，et al. Application of new fiber Bragg grating measurement in cable force monitoring of tied arch bridges［J］. Journal of Jiangsu University of Science and Technology （Natural Science Edition），2020，34（3）： 97-104.

［3］高欣，李冬生，邓年春，等. 拱桥吊杆荷载效应光纤光栅监测与安全评定［J］.大连理工大学学报，2006，46（增刊1）： 137-143.

GAO Xin，LI Dongsheng，DENG Nianchun，et al. Loading effects’ FBG monitoring system and safety evaluation of arch bridge suspenders［J］. Journal of Dalian University of Technology，2006，46（Sup1）： 137-143.

［4］张海东，田章华，段元锋，等. 基于磁弹效应的拱桥吊杆索力监测［J］. 结构工程师，2016，32（4）： 80-84.

ZHANG Haidong，TIAN Zhanghua，DUAN Yuanfeng，et al. Elasto-magnetic effect based suspender force monitoring of an arch bridge［J］. Structural Engineer，2016，32（4）： 80-84.

［5］殷志祥，宁志扬. 基于磁通量法的空间网架结构无损应力检测的试验方法研究［J］.防灾减灾工程，2020，40（5）： 803-810.

YIN Zhixiang，NING Zhiyang. Study on the test method of nondestructive stress test of space truss structure by magnetic flux method［J］. Journal of Disaster Prevention and Mitigation Engineering，2020，40 （5）： 803-810.

［6］BARNES M R. Form finding and analysis of tension structures by dynamic relaxation［J］. International Journal of Space Structures，1999，14（2）： 89-104.

［7］王俊，汪凤泉，周星德. 基于波动法的斜拉桥索力测试研究［J］. 应用科学学报，2005，23（1）： 90-93.

WANG Jun，WANG Fengquan，ZHOU Xingde. Wave-based study for cable tension measurement of cable-stayed bridge［J］. Journal of Applied Sciences，2005，23（1）： 90-93.

［8］CESCATTI E，PORTO F D A，MODENA C. Axial force estimation in historical metal tie-rods： methods，influencing parameters，and laboratory tests［J］. International Journal of Architectural Heritage，2019，13（3）： 317-328.

［9］DAI Tongtong，JIA Ziguang，REN Liang，et al. Modal analysis-based initial axial force recognition method for jacket platform［J］. Ocean Engineering，2022，262： 112279.

［10］GEUZAIME M，FOTI F，DENOEL V. Minimal requirements for the vibration-based3939a229654cede6cca70e67ca5d4de8 identification of the axial force，the bending stiffness and the flexural boundary conditions in cables［J］. Journal of Sound and Vibration，2021，511： 116326.

［11］RUSSELL J C，LARDNER T J. Experimental determination of frequencies and tension for elastic cables［J］. Journal of Engineering Mechanics，1998，124（10）： 1067-1072.

［12］李素贞，ROECK G D，REYNDERS E. 杆件轴力的一种识别方法［J］. 振动、测试与诊断，2011，31（6）： 694-699.

LI Suzhen，ROECK G D，REYNDERS E. Identification method for axial force of beam member［J］. Journal of Vibration，Measurement & Diagnosis，2011，31（6）： 694-699.

［13］LI Suzhen，REYNDER E，MAES K，et al. Vibration-based estimation of axial force for a beam member with uncertain boundary conditions［J］. Journal of Sound and Vibration，2013，332（4）： 795-806.

［14］LAGOMARSINO S，CALDERINI C. The dynamical identification of the tensile force in ancient tie-rods［J］. Engineering Structures，2005，27（6）： 846-856.

［15］AMABILI M，CARRA S，COLLINI L，et al. Estimation of tensile force in tie-rods using a frequency-based identification method［J］. Journal of Sound and Vibration，2010，329（11）： 2057-2067.

［16］袁永强，李东升，李宏男. 基于动力方法的改进杆件轴力识别［J］. 大连理工大学学报，2015，55（5）： 511-517.

YUAN Yongqiang，LI Dongsheng，LI Hongnan. Vibration-based improved identification of axial force for bar members［J］. Journal of Dalian University of Technology，2015，55（5）：511-517.

［17］LI Dongsheng，YUAN Yongqiang，LI Kunpeng，et al. Experimental axial force identification based on modified Timoshenko beam theory［J］. Structural Monitoring and Maintenance，2017，4（2）：153-173.

［18］李东升，李坤朋，魏达. 不同截面杆件轴力识别的理论与试验验证［J］. 振动工程学报，2019，32（1）： 151-159.

LI Dongsheng，LI Kunpeng，WEI Da. Theory and experimental verification of axial force identification of members with different cross sections［J］. Journal of Vibration Engineering，2019，32（1）： 151-159.

［19］李东升，陈琪舟，魏达，等. 不确定刚度和边界约束条件下的轴力识别［J］. 振动与冲击，2022，41（20）：208-215.

LI Dongsheng，CHEN Qizhou，WEI Da，et al. Axial force identification for uncertain stiffness and boundary constraints［J］. Journal of Vibration and Shock，2022，41（20）：208-215.

［20］GUYADER Jean-Louis. Vibration in Continuous Media［M］. Hoboken： John Wiley & Sons，2006.

［21］刘晶波，杜修力. 结构动力学［M］. 北京：机械工业出版社，2005.

LIU Jingbo，DU Xiuli. Structural Dynamics［M］. Beijing： Machinery Industry Press，2005.

［22］李坤朋. 杆件轴力识别技术的理论探讨与试验研究［D］. 大连：大连理工大学，2017.

LI Kunpeng. Theory investigations and experimental validation of axial force identification for bar members［D］. Dalian： Dalian University of Technology，2017.

An enhanced dynamic equation for Timoshenko beams based on the Reissner energy function and its application to axial force identification

GUO Xin1，WEI Da3，YAO Ya-dong1，2，LI Dong-sheng4

（1.Transportation Institute of Inner Mongolia University，Hohhot 010070，China；2.Inner Mongolia Engineering Research Center of Testing and Strengthening for Bridges，Inner Mongolia University，Hohhot 010070，China； 3.State Key Laboratory of Coastal and Offshore Engineering，Dalian University of Technology，Dalian 116024，China； 4. Guangdong Engineering Center for Structure Safety and Health Monitoring，Shantou University，Shantou 515063，China）

Abstract： The dynamic method for identifying axial force is grounded in vibration theory，making the vibration equation of a bar member crucial for accurate axial force estimation. Traditionally，the Timoshenko beam is derived from the equilibrium of transverse forces and moments. In this paper，an energy-based approach is applied to derive a new vibration equation for the Timoshenko beam under axial loading. The Ressiner energy equation for a Timoshenko beam，incorporating displacement，stress and axial force，is established using a condensation hypothesis from an energy perspective. The motion equation and stress equilibrium are calculated using the extremum principle，leading to a new free vibration equation for the Timoshenko beam under axial force. Compared to classical textbooks，the proposed dynamics equation includes two additional terms related to axial forces and shear effects. The new equation is validated through numerical simulations and laboratory experiments to identify the axial force in bar members. The results demonstrate that the proposed equation significantly improves the accuracy of axial force identification，confirming its correctness and applicability.

Key words： Timoshenko beam；free vibration；modal analysis；axial force identification

作者简介： 郭 鑫（1991―），男，博士，讲师。E-mail： guoxin@imu.edu.cn。

通讯作者： 李东升（1972―），男，博士，教授。电话： （0754）86502982； E-mail： lids@stu.edu.cn。