面向动态特性指标的机电伺服系统PID设计方法

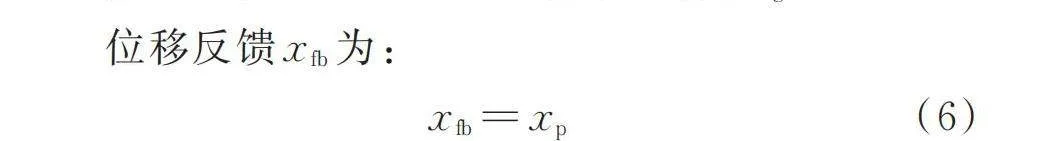
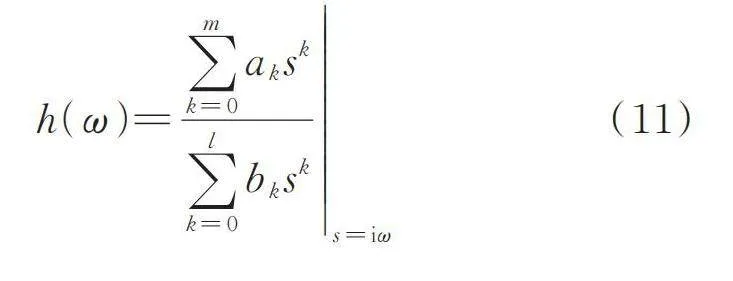
摘要： 针对机电伺服系统PID参数设计难以充分考虑动态特性（幅⁃相频特性）指标的问题，提出了面向动态特性指标的PID设计方法。基于动力学方程建立了机电伺服系统的9阶传递函数（Transfer Function，TF）模型。运用劳斯判据和TF系数之间的关系补充了系统的稳定性约束和TF系数的相容性约束，以保证PID设计过程中系统的稳定性和TF系数的相容性。在此基础上，基于参数辨识的思想，利用改进的有理分式多项式法辨识TF模型中各个参数，从而快速确定了满足动态特性指标的PID参数，提高了设计效率，并且通过调整指标数据辨识得到多组满足原指标的控制器参数。仿真结果表明：设计得到的PID参数不仅满足动态特性指标要求，而且兼顾了系统稳定性和TF系数的相容性，设计结果与仿真吻合良好。

关键词： PID控制； 参数辨识； 动态特性指标； 机电伺服系统

中图分类号： TP273； TM341 文献标志码： A 文章编号： 1004-4523（2024）10-1767-08

DOI：10.16385/j.cnki.issn.1004-4523.2024.10.015

引 言

伺服系统是飞行器控制系统的重要组成部分，通过接收来自控制系统的指令，控制空气舵偏转或喷管摆动来产生控制力，实现飞行器的姿态控制和轨迹控制［1］。随着功率电子技术的发展，以机电作动器（Electromechanical Actuator，EMA）为位移输出的机电伺服系统逐渐取代了液压伺服系统。由于取消了传统液压作动器内部的液压系统，EMA具有精度高、维护成本低、重量轻、环境适应性强等优点，近年来在航空航天领域得到广泛使用［2⁃5］。

机电伺服系统的控制算法一般包括PID控制［6］、神经网络控制［7⁃8］、自抗扰控制［9⁃10］、鲁棒控制［11］和滑模控制［12］等，其中常规PID控制由于结构简单、实时性好、鲁棒性较强等特点，在控制领域得到了广泛应用。但是PID控制的性能依赖于参数整定，目前，PID参数整定的方法主要分为以下几类：Ziegler⁃Nichols法、ISTE最优设定法、经验法、辨识法、开环阶跃响应曲线法、闭环测试法等［13］，上述方法大多是针对单闭环PID控制器进行设计的，且很大程度上和设计者的工程经验有关。针对该问题，李璀璀等［14］提出了基于遗传算法的模糊PID控制方法，提高了PID参数全局寻优的能力，且仿真结果表明，相较于模糊PID控制，该方法能明显改善电动舵机的动稳态性能；陈家俊等［15］以伺服系统为研究对象提出了一种基于机器学习和模糊控制的PID参数整定方法，该方法经过学习后能自动给出几组较优控制参数，避免了手动整定PID参数，节省了时间和人力成本；Pradhan等［16］提出了一种PID非线性自整定方法，该方法能在线辨识并实时更新模糊控制系统的参数，实现了对柔性机械手的高精度跟踪；邱亮［17］基于阶跃响应的模型辨识方法提出了一种PID控制器定量自整定方法，并开发了相应PID自整定软件，提高了控制器的自动化程度和控制精度；Davanipour等［18］采用混沌优化方法提出了一种基于模糊小波神经网络模型的自整定PID控制器，实验表明自整定得到的PID参数有较好的控制性能，系统响应的稳态误差小，跟踪性较好。以上研究工作对PID的设计提供了思路。然而，上述方法的设计目标大多基于控制精度，面向动态特性指标的PID设计研究还鲜有报道。

伺服系统的动态特性对姿态控制系统设计有重要影响，因此，姿控专业对其提出了严格的指标要求，包括幅频特性和相频特性两方面。工程中，不同飞行器的空气舵或摆动喷管转动惯量不同，当选用现成的伺服系统进行飞行器姿态控制时，往往需要考虑在不改变伺服系统硬件的情况下，通过调整PID控制参数使其满足指标要求。针对以上问题，本文以采用PID控制的机电伺服系统为研究对象，建立了系统的9阶传递函数（Transfer Function，TF）模型，在约束条件下利用动态特性指标数据设计出了满足指标要求的PID参数MMoE6yxAfOYDONF/rIj/qg==，用建立的SIMULINK非线性仿真模型验证了该方法的正确性。

1 机电伺服系统建模

1.1 系统组成

机电伺服系统由驱动控制器和EMA组成，如图1所示，其工作原理为：驱动控制器接收来自控制系统的位置指令和电源输入，驱动电机输出转速和扭矩，然后通过齿轮机构和滚珠丝杠轴带动滚珠螺母输出直线位移，最后传感器反馈位移形成闭环控制。由于电压和功率有限，因此驱动控制器存在电气饱和的非线性因素。

1.2 系统非线性动力学

机电伺服系统是一个有电流环、速度环、位置环的三环控制系统［19］，为满足伺服系统快速、精确控制的需求，一方面通过选择合适的元器件使传感器、控制器和执行机构之间的延迟尽量小，另一方面要求电流环调节器具有较高的带宽和较小的时间常数，同时在EMA电机和控制器选型时一般要求其电气时间常数远小于机械时间常数，因此，在总体集成建立动力学模型时可以忽略伺服电机电流环控制的动态［2］。故本文驱动控制器采用位移反馈、电机速度反馈和PID控制实现对控制系统位置指令的闭环跟踪，动力学建模如下［20］：

控制器输出电压为：

（1）

式中 分别为PID控制器的比例增益、积分增益和微分增益；为电机速度反馈增益；为电机转角；为电机速度；为控制系统输入的位置指令；为位移反馈。

电机速度方程为：

（2）

其中，电机向滚珠丝杠输出的扭矩为：

（3）

式中 为电机转动惯量；为Laplace域复变量；为电机带宽；为电机转矩增益；为相对角位移（电机负载）；为滚珠丝杠齿轮转角；为减速比（电机转角与滚珠丝杠转角比）；为齿轮副刚度；为电机齿轮摩擦系数；为电机库伦摩擦力矩幅值。

作动轴的位置为：

（4）

式中 为丝杠及其齿轮的转动惯量；为齿轮副的机械效率；为滚珠丝杠传动比（丝杠转动1 rad对应的活塞伸长量）；为滚珠丝杠阻尼系数；为活塞轴受到的力；为舱壁、作动器和负载串联的总刚度；为活塞轴到负载旋转轴的力臂；为负载转角；为活塞伸长量；为活塞轴端部实际位移。

负载绕转轴转动，运动方程为：

（5）

式中 为负载绕转轴的转动惯量，通过减速比关系折算到电机输出轴上；为黏性阻尼系数；为外界输入力矩；为负载绕转轴的转动刚度，对于空气舵和球窝摆动喷管这类操纵机构，=0。

位移反馈为：

（6）

由于EMA性能受负载、非线性等因素影响较大，考虑到工程实际，为优化伺服系统的性能，改善系统稳定性、降低噪声干扰和保护关键组件，通常在控制器中加入一个低通滤波器，其传递函数为：

（7）

式中 为滤波器参数。

综上所述，机电伺服系统是一个复杂的非线性系统，综合式（1）～（7）可建立如图2所示的非线性仿真模型，用于后续仿真检验。

1.3 系统传递函数

伺服系统的动态特性一般采用简谐或扫频激励测试获得。工程中空载测试时，外界输入力矩，负载可采用一个刚体惯量盘。不计式（7）滤波器和摩擦的影响，对式（1）～（5）进行Laplace变换，得到整个系统的TF：

（8）

其中：

其中：

考虑滤波器时，系统的TF可由与相乘得到，此时TF的形式为：

（9）

其中，与的系数表达式均已给出，，的表达式可由与的系数相乘得到，这里不再一一给出。对于系统零次项系数，在不考虑滤波器时有，考虑滤波器时有，表示在静态和低频输入指令时，系统响应与偏转指令是1∶1传递，体现了位置跟踪系统的特征。

2 面向动态特性指标的PID设计方法

对于式（9）中的传递函数，当系统参数确定时，各系数均只为的函数。通过动态特性指标设计可以转换为参数辨识问题，即尝试通过用式（9）的传递函数拟合动态指标数据得到满足指标的，，进而由，确定PID控制参数。

实际的参数辨识一般不直接进行传递函数的测试，而是通过频响测试完成传递函数参数的辨识。在本文PID参数设计的问题中，将动态特性的指标数据作为测试数据进行辨识。

式（9）对应的频响函数为：

（10）

式中 i为虚数单位。

2.1 带约束的有理分式正交多项式法

式（10）的参数辨识问题最终可以通过求解一组线性方程来得到最小二乘误差意义上的解，但最大的困难在于方程组是病态的。对此，Richardson等［21］提出了有理分式正交多项式法，用复正交多项式重新表征频响函数，可使数值病态问题得到有效改善。该方法是针对一般的线性系统提出的，不能直接处理约束条件，需要对其进行改进，在目标函数中补充约束方程。一般线性系统的频响函数均可表示为如下式的有理分式：

（11）

式中 和为待辨识的参数。C2ED2+wa0jUqOfYWGXByvl+rgd9LV1kEM2iTUQqc9R4=

在每个测试频点上将频响函数改写为用半函数表示的正交多项式：

（12）

式中 和为Forsythe多项式（半函数）的正交基，满足正交条件：

（13）

（14）

式中 上标“*”表示共轭。当求解出频响函数中的系数和时，即可通过转换矩阵求解得到传递函数中的系数和：

（15）

式中 ；；；；，为转换矩阵。同时，不失一般性，假设分母最高阶系数。

此时用正交多项式表示的误差向量为：

（16）

2.2 构造目标优化函数

参数辨识本质上是一个优化问题，因此可构造最小二乘拟合目标函数：

（17）

对于给定的系统，被控对象参数已知时，只为PID控制器3个参数的函数。

对于式（11）的频响函数，含有个未知系数和3个自由度，即存在个系数之间的约束条件。

同时，为保证采用PID控制后伺服系统的稳定性，系统特征方程的系数需要满足稳定判据。因此，运用劳斯判据可得到个稳定性约束，加上系数之间的约束总共有个关于，的约束。这些约束可通过转换矩阵加到目标函数中，最终问题可转换为求解约束条件下的多参数优化问题，数学上可表述为求使最小，即

（18）

式中 为系数之间的等式约束，由于劳斯判据中包含系数的乘积，因此为待求系数的非线性不等式约束。对于式（18）的优化问题，可利用MATLAB非线性规划求解器fmincon进行求解，fmincon通过使用拉格朗日乘子法能够有效处理等式和不等式约束，并结合内点法、序列二次规划法等方法来寻找最优解。求解得到正交多项式的系数向量和后，通过转换矩阵变换即可得到传递函数的系数和，进而根据，与PID参数的关系求得，完整的PID设计流程如图3所示。

3 数值仿真检验

3.1 数值仿真案例

工程中伺服系统的动态特性指标往往是在特定的离散频点上给出的，表1为某机电伺服系统的动态特性指标数据。当将指标数据作为测试数据进行PID设计时，可用插值的方法将所有频点上的指标数据补全，当用线性插值补全所有指标数据时，辨识结果见表2。

3.2 结果分析与讨论

将表2中辨识的PID参数代入非线性仿真模型进行检验，输入伺服正弦扫频指令，输出伺服摆角，由二者可得到幅频和相频特性，结果如下：

（1） 用补全的动态特性指标数据进行辨识能够得到满足指标的PID参数，，，辨识结果分别为665.2，100.3，3.12。将辨识得到的PID参数代入仿真模型进行验证，结果如图4所示，其中曲线（拟合结果）为对原指标数据的拟合情况，即辨识得到的PID参数对应的动态特性。扫频幅值为0.25°和0.5°时，仿真结果与辨识结果吻合良好，此时控制器电压未饱和，摩擦等非线性因素对幅频和相频的仿真结果影响较小，两个扫频幅值下的仿真结果几乎重合；扫频幅值为2°时，由于控制器电压饱和，系统饱和非线性对幅频特性的影响明显，幅频仿真数据出现“削峰”现象，但依然满足指标要求。

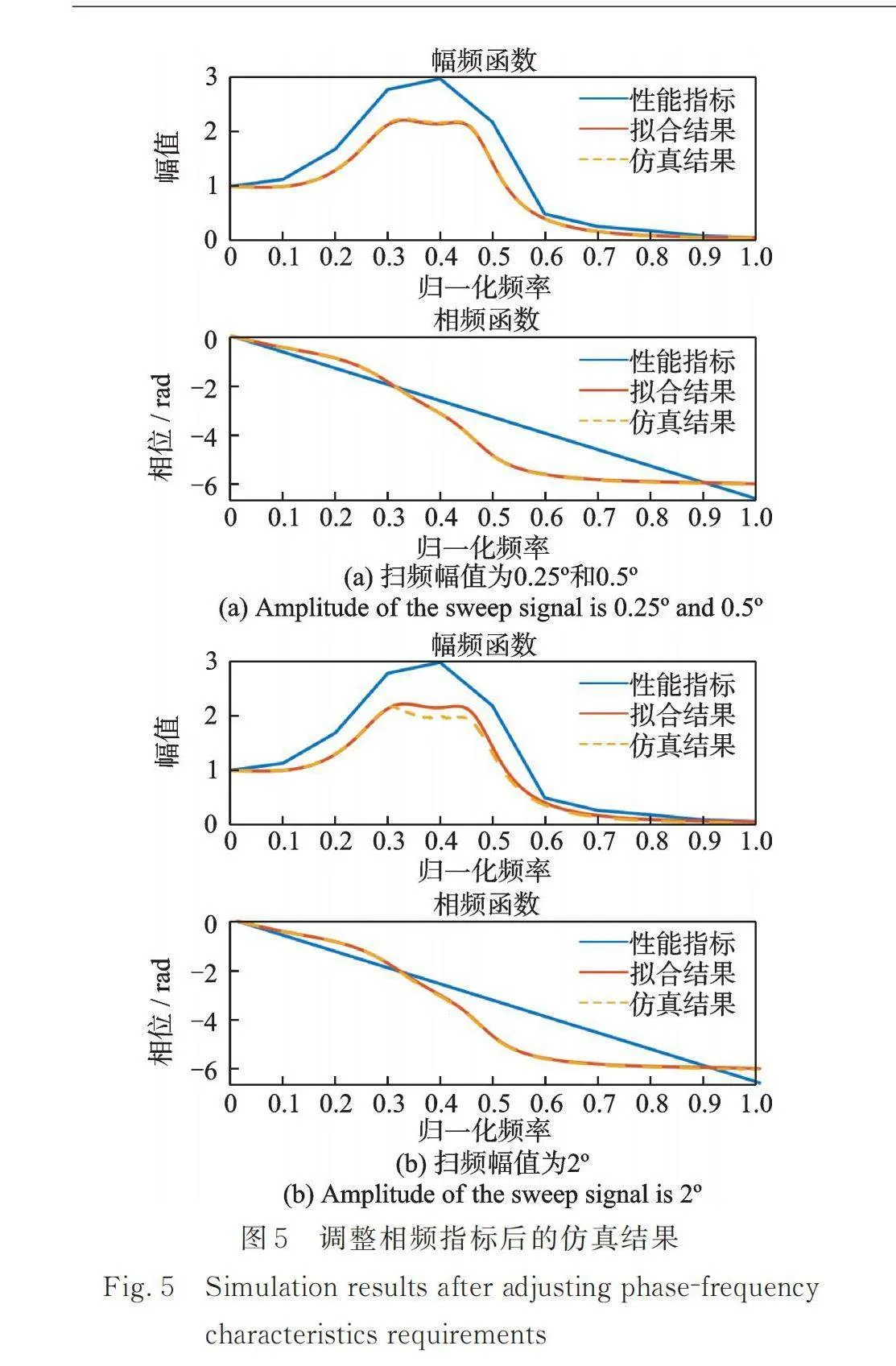
（2） 基于优化理论得到的辨识结果是满足约束条件下与指标数据误差最小的一组参数，实际满足指标的参数可能不止一组，理论上适当调整原指标数据可得到满足指标的另一组PID参数。调整方法为：通过增大或减小离散频点上的幅频和相频指标数据，直至辨识出满足原指标要求的另一组PID参数。图5为在不改变幅频指标的情况下，将相频指标的插值斜率增大到原来的1.25倍得到的另一组PID参数的仿真结果，，，的辨识结果分别为584.6，102.1，3.38。扫频幅值为0.25°和0.5°时，仿真结果与辨识结果吻合良好，两个扫频幅值下仿真结果几乎重合；扫频幅值为2°时，幅频仿真数据出现“削峰”现象，依然满足原指标。

（3） 实际的辨识结果在全频段内可能不完全满足指标要求，需要适当调整原指标数据才能得到满足指标的结果。由于相频指标只在低频段内提出，相较于相频，幅频更3f380c5ffaa717de74bc562df25534dc容易超出指标。因此，当辨识的结果超过指标时，指标调整依据为：把原幅频指标数据适当下移，由于相频数据变化具有相似性，可以用上一步辨识的相频数据将相频指标补全，减小补全的相频数据对辨识结果的影响。如图6所示，其中曲线（调整指标）为原指标调整后用于辨识的指标数据，相较于原指标，此处幅频指标在各个频点上分别下调0.01，0.12，0.32，1.05，1.69，1.35，0.25，0.17，0.13，0.05，0.03。用调整后的指标数据重新进行辨识，，，的辨识结果分别为413.1，37.1，2.04，在幅值为0.25°，0.5°和2°的扫频指令下均满足原指标，且控制器电压未饱和，仿真结果与辨识结果吻合良好，三个扫频幅值下的仿真结果几乎重合。相较于图4和图5的设计结果，图6得到的结果非线性影响更小，而且在确保相位滞后满足性能指标的同时，中低频段更接近理想的1∶1传递。

（4） 由于在设计时加入了传递函数系数之间的约束和稳定性约束，设计结果符合位置跟踪系统的特征，在低频部分的幅频传递特性趋于1∶1，相位差趋于0。

4 结 论

伺服系统动态特性对飞行器姿态控制设计具有重要影响。本文以机电伺服系统为对象，面向满足动态特性指标的PID控制设计需求，基于参数辨识思想，提出带约束的有理分式正交多项式法，完成了PID参数的设计。得到以下结论：

（1） 该方法将系统稳定性要求和传递函数系数间的关系表达为曲线拟合的约束条件，使得PID参数设计过程同时兼顾了动态特性指标、系统稳定性和TF系数相容性三方面要求，确保PID控制设计的有效性，提高了设计效率。

（2） 仿真实验表明，设计结果满足动态特性指标要求，且通过适当调整拟合指标数据可以得到多组满足指标的控制器参数，然后，结合动态特性和其他伺服系统特性要求确定最终选择哪组参数。

（3） 本文的设计方法是面向一般的线性系统提出的。如果伺服系统控制设计需要考虑电流环控制，则只需要在系统动力学模型和传递函数中补充电流环环节后，同理采用带约束的参数辨识方法完成PID参数设计即可。

参考文献：

［1］朱忠惠，陈孟荦．推力矢量控制伺服系统［M］.北京： 中国宇航出版社，1995．

［2］刘博，祝学军，南宫自军，等.电动空气舵执行机构建模与参数辨识［J］. 宇航学报，2017，38（11）： 1147-1152.

Liu Bo，Zhu Xuejun，Nangong Zijun，et al. Modeling and parameter identification of an aircraft rudder system with an electromechanical actuator［J］. Journal of Astronautics，2017，38（11）： 1147-1152.

［3］吕晨，欧阳权，徐文波，等. 基于干扰观测器的机电伺服系统PI控制策略［J］. 机床与电液，2024，52（1）：17-22.

Lü Chen，Ouyang Quan，Xu Wenbo，et al. Interference observer-based PI control strategy of electromechanical servo system［J］. Machine Tool & Hydraulics，2024，52（1）：17-22.

［4］张茂盛，段杰，肖息，等. 基于深度强化学习-PI控制的机电作动器控制策略［J］.应用科技，2022，49（4）：19-22.

Zhang Maosheng，Duan Jie，Xiao Xi，et al. Control strategy of electro-mechanical actuator based on deep reinforcement learning-PI control［J］. Applied Science and Technology，2022，49（4）：19-22.

［5］鹿山山，王志胜，欧阳权，等. 飞机机电作动器模糊 PI-ANN复合控制仿真［J］. 兵器装备工程学报，2021，42（10）： 158-164.

Lu Shanshan，Wang Zhisheng，Ouyang Quan，et al.Simulation of compound control based on fuzzy PI and artificial neural network for aircraft electromechanical actuation systems［J］. Journal of Ordnance Equipment Engineering，2021，42（10）： 158-164.

［6］尚东阳，李小彭，尹猛，等.采用干扰补偿模糊整定的双柔性机械臂抑振策略［J］.振动工程学报，2024，37（1）：1-10.

Shang Dongyang，Li Xiaopeng，Yin Meng，et al. Vibration suppression strategy of dual-flexible manipulator using disturbance compensation fuzzy setting control method［J］.Journal of Vibration Engineering，2024，37（1）：1-10.

［7］Liu H M，Jing J Y，Ma J. Fault diagnosis of electromechanical actuator based on VMD multifractal detrended fluctuation analysis and PNN［J］. Complexity，2018，2018： 9154682.

［8］朱志忠，袁鑫，赵丰，等. 考虑作动器输出饱合的光电平台终端滑模神经网络控制［J］. 振动与冲击，2022，41（21）：161-167.

Zhu Zhizhong，Yuan Xin，Zhao Feng，et al. Sliding mode neural network control of optoelectronic platform terminal considering actuator output saturation［J］. Journal of Vibration and Shock，2022，41（21）：161-167.

［9］魏泽宇，许文波，张国林，等. 航天机电伺服系统的自抗扰控制［J］. 控制理论与应用，2021，38（1）： 73-80.

Wei Zeyu，Xu Wenbo，Zhang Guolin，et al. Active disturbance rejection control of aerospace electromechanical servo system［J］. Control Theory&Applications，2021，38（1）： 73-80.

［10］赵希梅，陈广国，金鸿雁. 基于改进灰狼优化算法的PMSM滑模自抗扰控制［J］. 电机与控制学报，2022，26（11）：132-140.

Zhao Ximei，Chen Guangguo，Jin Hongyan. Sliding mode active disturbance rejection control for PMSM based on improved grey wolf optimization algorithm［J］. Electric Machines and Control，2022，26（11）：132-140.

［11］王烨波，刘家辉，卫健，等. 机电伺服系统积分鲁棒自适应控制［J］.科技创新与应用，2021，11（23）：7-11.

Wang Yebo，Liu Jiahui，Wei Jian，et al. The integral robust adaptive control of mechatronic servo system［J］. Technology Innovation and Application，2021，11（23）：7-11.

［12］Rubio J. Sliding mode control of robotic arms with deadzone［J］. IET Control Theory&Applications，2017，11（8）： 1214-1221.

［13］张磊，苏为洲. 伺服系统的反馈控制设计研究综述［J］. 控制理论与应用，2014，31（5）：545-559.

Zhang Lei，Su Weizhou. Feedback control design of servo systems： a review［J］. Control Theory&Applications，2014，31（5）：545-559.

［14］李璀璀，易文俊，管军，等. 基于遗传算法的电动舵机系统模糊PID控制［J］. 兵器装备工程学报，2021，42（3）：162-167.

Li Cuicui，Yi Wenjun，Guan Jun，et al. Fuzzy PID control of electromechanical actuator system based on genetic algorithm［J］. Journal of Ordnance Equipment Engineering，2021，42（3）：162-167.

［15］陈家俊，贺云波. 伺服系统中PID控制器参数整定的研究［J］. 机床与电液，2021，49（1）：13-16.

Chen Jiajun，He Yunbo. Study on parameter tuning for PID controller in servo system［J］. Machine Tool&Electro-Hydraulic，2021，49（1）：13-16.

［16］Pradhan K S，Subudhi B．Position control of a flexible manipulator using a new nonlinear self-tuning PID controller［J］. IEEE/CAA Journal of Automatica Sinica，2020，7（1）：136-149.

［17］邱亮. 基于阶跃辨识的 PID 自整定算法研究及其应用［D］. 上海：上海交通大学，2013.

Qiu Liang. Research and application of PID auto-tuning control method based on step identification［D］. Shanghai：Shanghai Jiao Tong University，2013.

［18］Davanipour M，Javanmardi H，Goodarzi N. Chaotic self-tuning PID controller based on fuzzy wavelet neural network model［J］. Iranian Journal of Science and Technology，Transactions of Electrical Engineering，2018，42（3）：357-366.

［19］李建明，蒋孟龙，安林雪，等. 机电作动器动力学建模与电流跳变现象分析［J］. 电机与控制学报，2020，24（1）：104-110.

Li Jianming，Jiang Menglong，An Linxue，et al. Dynamic modeling and current jump analysis of electro-mechanical actuator［J］. Electric Machines and Control，2020，24（1）：104-110.

［20］Falangas E T. Performance Evaluation and Design of Flight Vehicle Control Systems［M］. Hoboken，New Jersey：Wiley，2015.

［21］Richardson M H，Formenti D L. Parameter estimation from frequency response measurements using rational fraction polynomial［C］∥ Proceedings of the International Modal Analysis Conference&Exhibit，1982： 167-182．

Design method of PID control for electromechanical servo system based on dynamic characteristics requirements

CHEN Guo-rong，NANGONG Zi-jun，LIU Bo

（China Academy of Launch Vehicle Technology，Beijing 100076，China）

Abstract： In order to solve the problem that it is difficult to fully consider the dynamic characteristics （amplitude-phase frequency characteristics） requirements in the PID parameter design of electromechanical servo system，a PID design method for dynamic characteristics is proposed. The 9-order Transfer Function （TF） model of electromechanical servo system is established based on dynamic equation. The relationship between Routh criterion and TF coefficient is used to supplement the stability constraint of the system and the compatibility constraint of TF coefficient to ensure the stability of the system and the compatibility of TF coefficient in the PID design process. On this basis，based on the idea of parameter identification，the rational fraction orthogonal polynomial method is used to identify the coefficients in the TF model，so that the PID parameters are quickly determined，which improving the design efficiency，and multiple groups of controller parameters that meet the original index can be identified by adjusting the index data. The simulation results show that the designed PID parameters not only meet the requirements of dynamic characteristics，but also take into account the compatibility of system stability and TF coefficient. The design results are in good agreement with the simulation experiments.

Key words： PID control；parameter identification； electromechanical servo system；dynamic characteristics requirements

作者简介： 陈国荣（1999―），男，硕士研究生。电话： （010）88520510； E-mail：chen_gr1111@163.com。

通讯作者： 南宫自军（1968―），男，博士，研究员。电话： （010）68758120； E-mail：nangongzijun@yeah.net。