非线性俘能系统机电耦合动力学模型分析及故障诊断应用研究

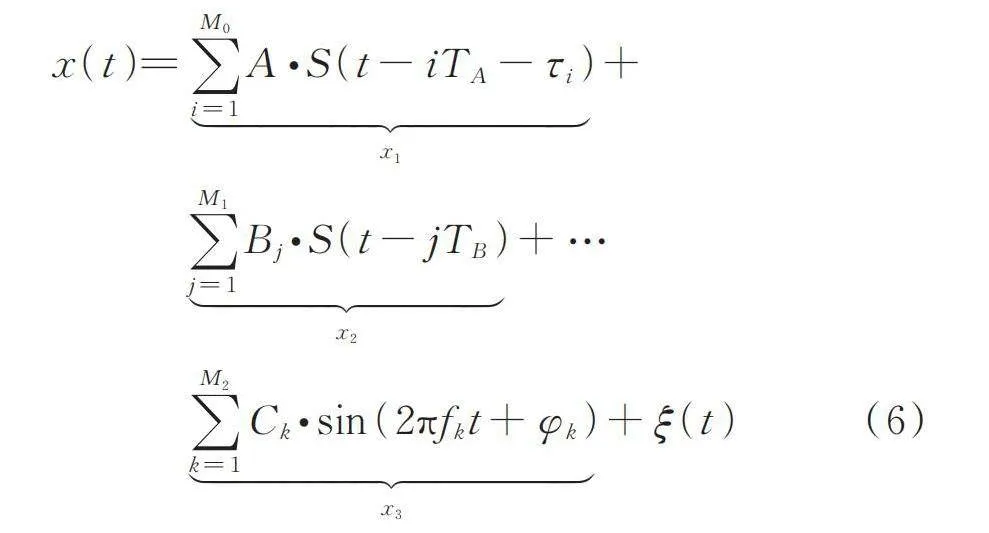
摘要： 研究势阱参数对非线性俘能系统输出特性的影响有利于设计高性能的俘能系统；同时，俘能系统对应的机电耦合动力学模型中的随机共振现象可用于增强微弱故障特征，进而有效识别微弱故障。本文提出一种解耦的鞍点退化双稳态势能函数，并基于此势能函数介绍了机电耦合动力学模型。研究了在不同激励幅值下位移响应的分岔图，分析了势阱宽度与势阱高度对系统响应（包括周期响应与混沌响应）的影响。选取固定的激励幅值，利用庞加莱映射（Poincaré Map）、频谱分析（Frequency Spectrum Analysis）以及李雅普诺夫指数（Lyapunov Exponent）等方法分别验证系统发生了周期响应与混沌响应，验证结果与分岔图相吻合。基于受随机噪声扰动的非线性俘能系统机电耦合动力学模型，提出了基于此模型随机共振的故障诊断方法，实现了对轴承故障特征增强的目的。

关键词： 非线性系统； 能量俘获； 故障诊断； 李雅普诺夫指数； 庞加莱映射

中图分类号： O322； TM619； TH165+.3 文献标志码： A 文章编号： 1004-4523（2024）10-1714-09

DOI：10.16385/j.cnki.issn.1004-4523.2024.10.009

引 言

随着无线传感技术的快速发展，微型低功耗传感器已广泛应用于人体健康监测［1］、重大机械设备的结构健康监测系统［2］，以及轨道交通基础设施状态监测系统等［3‑4］。但传统的微型传感器大部分需要化学电池供能，这种供能形式需要定期更换电池，且更换的电池对环境有害。利用能量俘获技术俘获环境中的风能［5‑6］、海洋能［7‑8］以及低频振动能量［9‑10］等绿色能源可实现对微型低功耗传感器的长期供能。针对不同的激励形式，研究学者分别研究了基础激励、气动激励、旋转激励以及随机激励等的振动能量俘获系统（简称“俘能系统”）。Zhou等［11］推导了基础激励下非对称三稳态俘能系统的谐波平衡解，揭示了其中的非线性动力学机制。Huang等［12］利用谐波平衡法获得了基础激励下非对称四稳态俘能系统的理论解，并分析了不同的势阱深度对阱间振动的影响。Tai等［13］推导了基础激励下基于最大功率的优化条件。Li等［14］利用增量谐波平衡法理论分析了三稳态颤振式俘能系统的周期解和分岔，并通过风洞试验进行了验证。Huang等［15］利用复变量平均法理论推导了驰振和基础激励下俘能系统的理论解，并分析了其动力学性能。Hou等［16］研究了在涡激振动和基础激励下的压电‑电磁混合俘能系统。相比单一涡激振动或单一基础激励下的俘能系统，俘获的能量功率得到了提高。Mei等［17］提出了具有时变特征的四稳态俘能系统，用于俘获低频旋转能量。在旋转运动下，俘能系统的有效工作频率范围为1～7 Hz。Wang等［18］研究了旋转环境下梯形梁俘能系统。与矩形梁相比，在夹具附近，梯形梁可以承受更高的应力。Fang等［19］利用膨胀的离心软化效应提出了超低频旋转运动下的俘能系统，其功率密度为41.23 μW/g。

非线性系统随机共振现象已广泛应用于工程领域［20］，如图像增强［21‑22］、能量俘获［23‑24］以及故障诊断［25‑26］。其原理是：在合适强度噪声干扰下，非线性系统会发生随机共振，使系统输出幅值达到最大。Kim等［27］利用自调节随机共振的优点，提出了一种用于调制噪声激励下旋转运动的能量俘获系统。与其他用于轮胎的俘能系统相比，该系统具有更大的功率输出和有效带宽。Gong等［28］研究了多稳态俘能系统的随机共振现象，用于增强在随机旋转激励下的能量俘获性能。Shi等［29］基于改进的非对称随机共振模型，阐述了如何利用噪声使系统发生随机共振进而改进俘能系统能量俘获效率。同样地，随机共振现象在故障诊断领域也有重要的应用。Lai等［30］基于双稳态Duffing系统，提出了一种尺度变换方法，可以将随机共振方法应用于大参数信号。Lei等［31］基于稳态匹配的欠阻尼随机共振方法，实现了滚动体轴承的早期故障诊断。此方法能够通过优化尺度因子抑制多尺度噪声的干扰。张刚等［32］研究了二维双阱势系统随机共振机理，并将其用于实际工业轴承故障诊断，提高了故障频率处峰值的辨识度。贺利芳等［33］提出了高斯势分段双稳随机共振系统，分别研究了在高斯白噪声和有色噪声下衡量指标随系统参数的变化规律。

非线性俘能系统具有复杂的机电耦合动力学响应，如果能把其中的随机共振现象应用于故障诊断领域，既能扩大俘能系统的应用范围，又能丰富基于随机共振的机械装备故障诊断方法。因此，本文也探索了非线性俘能系统机电耦合动力学模型随机共振现象在故障诊断中的潜在应用。

1 无量纲动力学模型

Yang等［34］研究发现非线性退化（鞍点退化与中心点退化）可以使非线性系统在超低频或低随机激励强度下实现大幅值的阱间振荡，可有效提高低激励水平下的能量俘获性能。因此，本节首先基于鞍点退化双稳态势能函数研究退化势能函数的势阱宽度与势阱高度对压电俘能系统响应的影响。其对应的无量纲机电耦合方程［35］可写为：

（1）

（2）

式中 表示系统位移响应；表示系统输出电压；表示无量纲的等效电容；表示无量纲的等效机电耦合系数； 表示无量纲的等效电阻；表示无量纲的等效阻尼； 表示无量纲的基础激励幅值；表示无量纲的基础激励的角频率。若俘能系统为对称双稳态系统，则无量纲的非线性力可表示为：

（3）

令式（3）等于零，则其对应有一个零根，两个虚根和两个实根。而若将式（3）中的项去除，则新的将对应有三个零根，两个实根。在文献［34］中，这种具有三个零根，两个实根的对应的势能函数称为鞍点退化势能函数。此时，可表示为［34］：

（4）

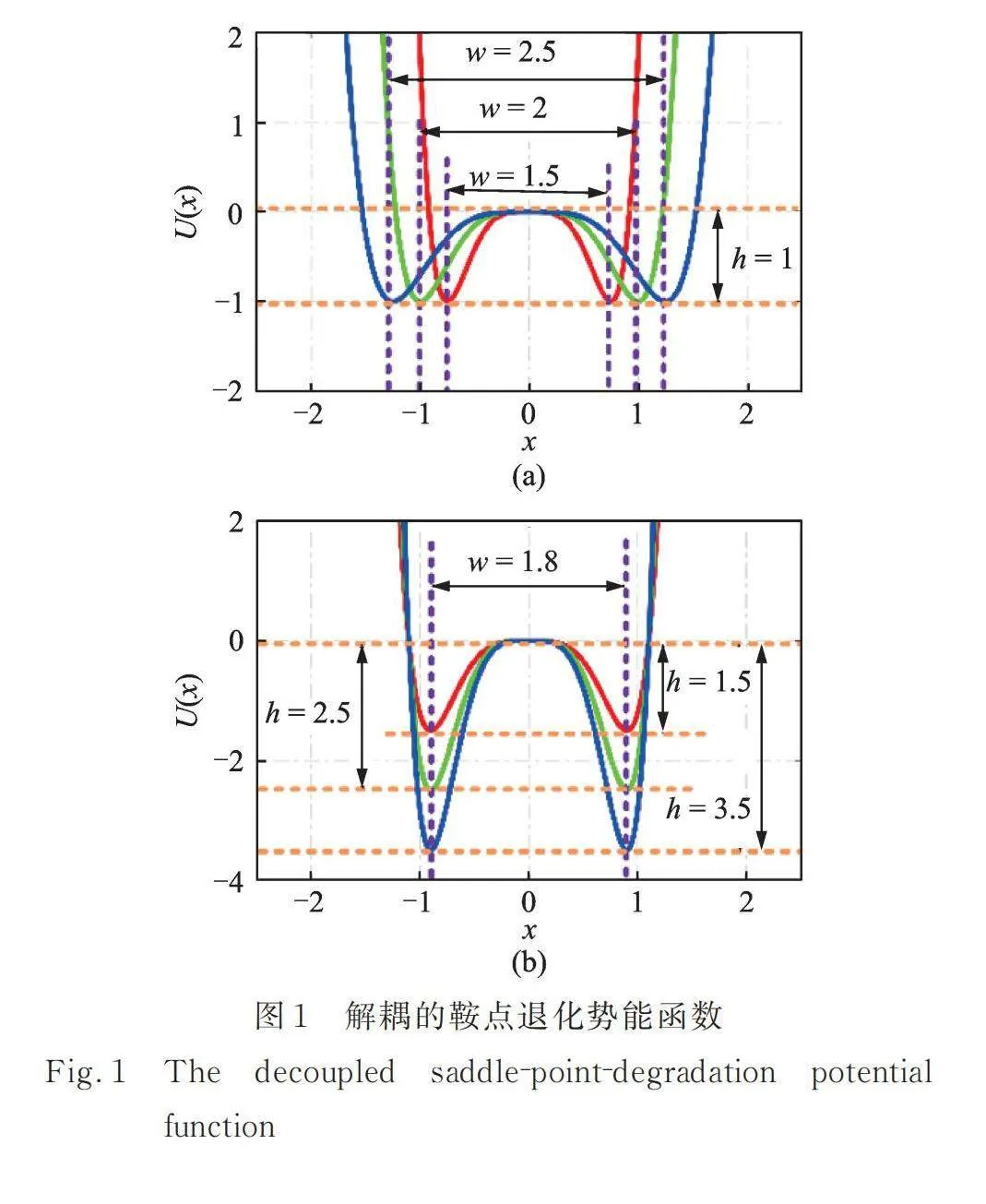
式中 表示非线性力系数；表示退化双稳态势能函数的稳定平衡点；表示势能函数对求导。因此，鞍点退化势能函数的势阱宽度，势阱高度。

对鞍点退化势能函数进行解耦，可得关于势阱宽度与势阱高度的解耦势能函数：

（5）

如图1所示，解耦的鞍点退化势能函数可由势阱宽度或势阱高度独立控制，即当势阱宽度变化时，可以保证势阱高度不变；势阱高度变化时，可以保证势阱宽度不变。这方便研究势阱宽度与势阱高度对非线性俘能系统的影响。

2 数值分析

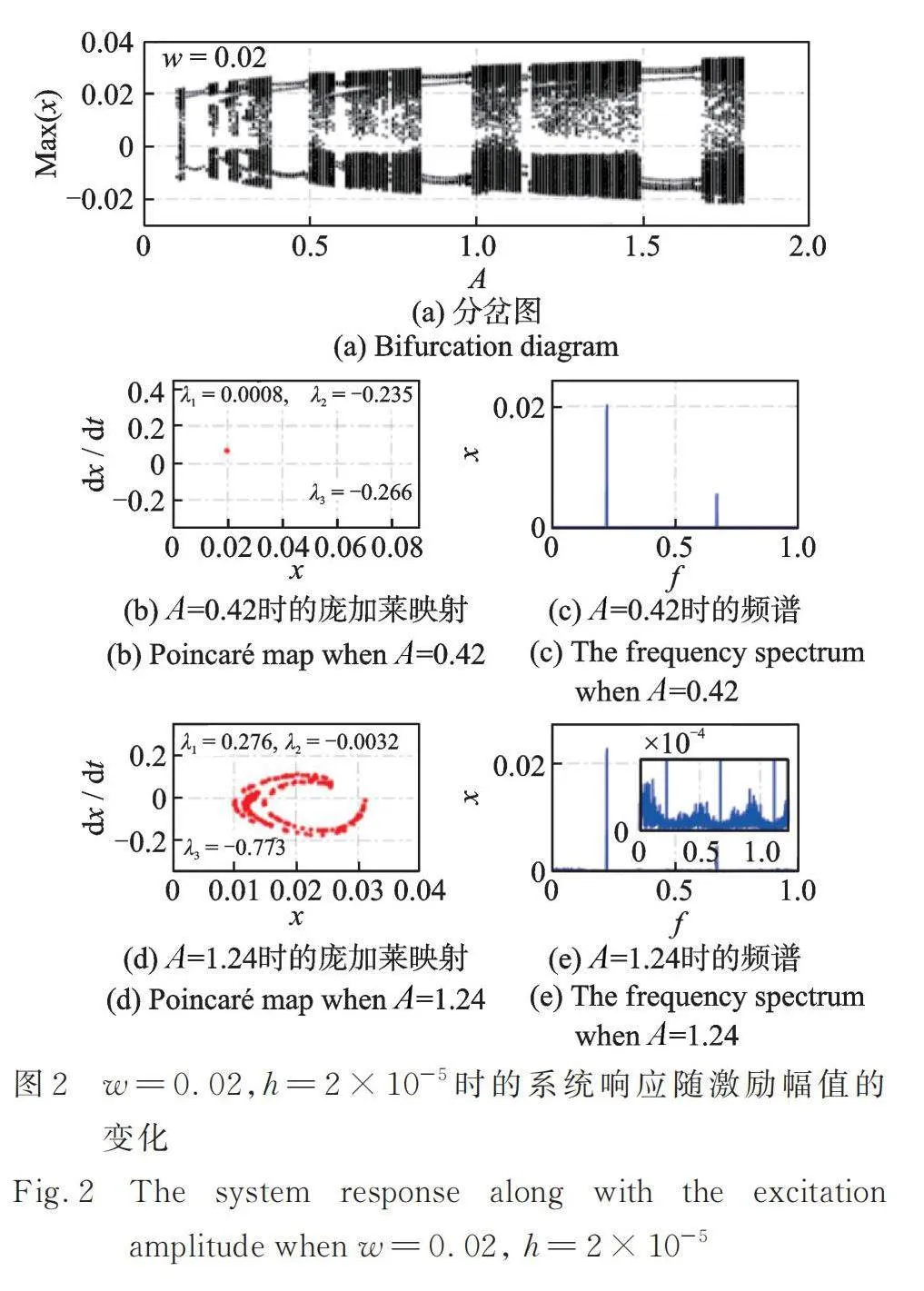
本节利用分岔图［36‑37］（分岔图是计算不同参数下稳定位移响应的幅值而获得的幅值分布图）研究了势阱宽度与势阱高度对系统响应（周期响应与混沌响应）的影响，可进一步反向指导特定激励强度下具有周期响应的俘能系统的结构设计。在数值分析过程中，无量纲激励幅值以0.01的步距从0.1变化到1.8，其他的无量纲参数分别为：，，，，。图2～8展示了不同势阱宽度与势阱高度下的分岔图、庞加莱映射（Poincaré Map）、频谱图以及李雅普诺夫指数（Lyapunov Exponent，本文的机电耦合系统对应有三个李雅普诺夫指数，分别表示为：，，）。

2.1 势阱宽度对系统响应的影响

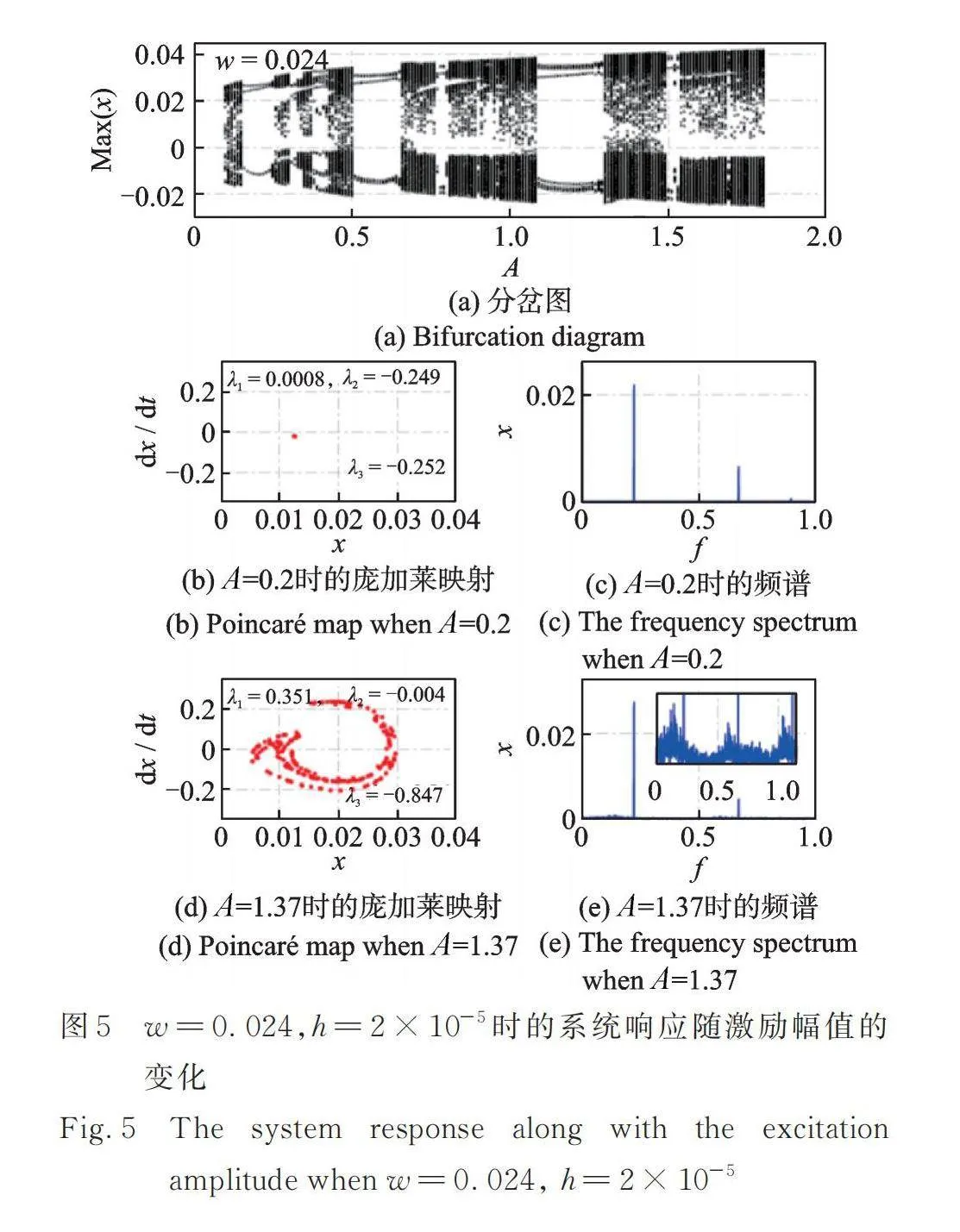
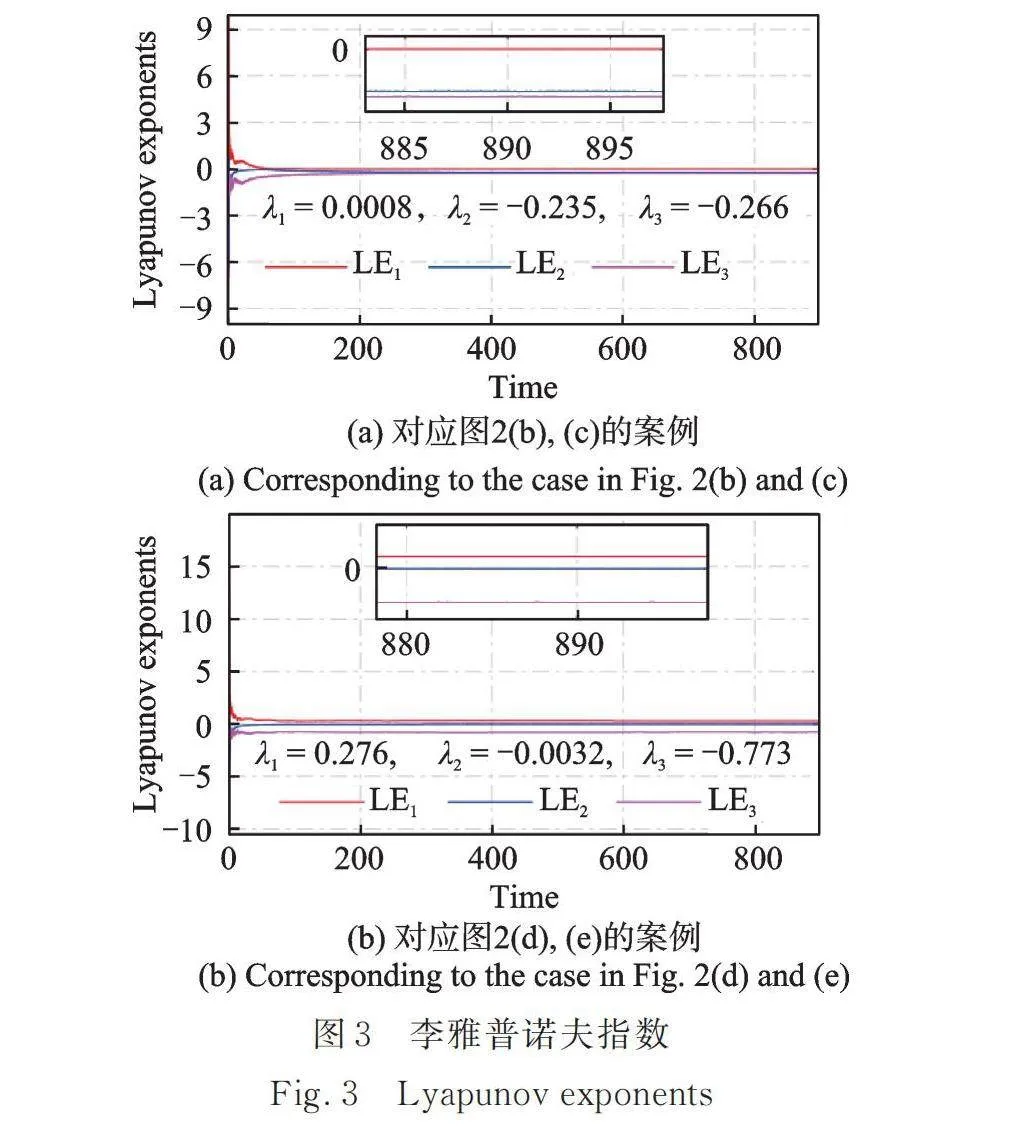
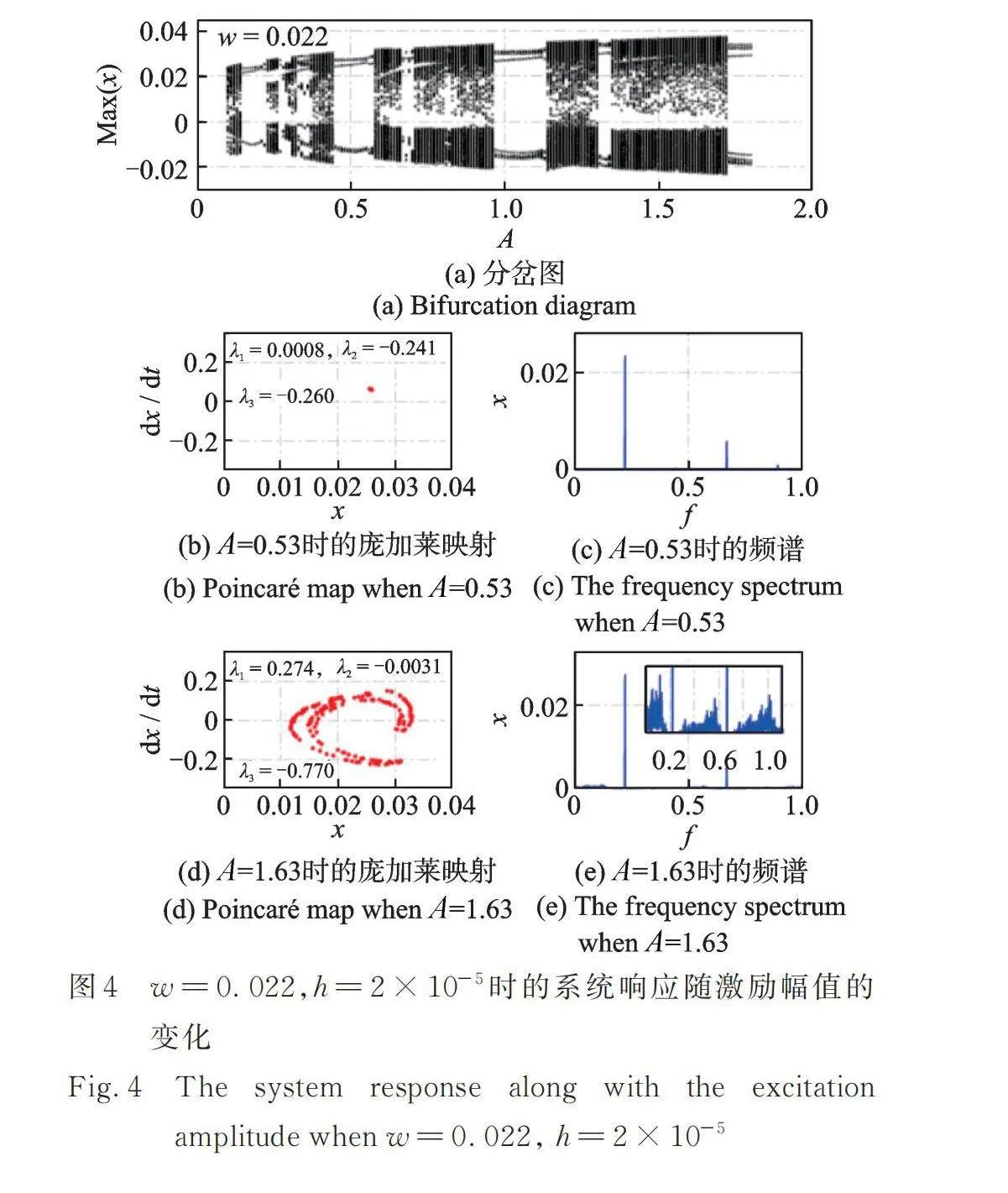
图2～5展示了当势阱高度时，不同势阱宽度下非线性俘能系统响应随激励幅值的变化。其中，图3详细展示了图2中李雅普诺夫指数随时间的变化趋势（其他图中的最终李雅普诺夫指数值已在图中标明）。从图2，4和图5中可以看出，随着势阱宽度的增大，非线性俘能系统发生混沌响应的区域将会整体朝着激励幅值增大的方向移动。在低激励幅值处的混沌区域将会变大。在特定的激励幅值下，系统发生周期响应时，其庞加莱映射为单个点，频谱中仅有明显的单频及其倍频成分，最大的李雅普诺夫指数［38‑39］（）约为0。当系统发生混沌响应时，其庞加莱映射具有明显的轨迹，频谱呈现明显的多频成分，最大李雅普诺夫指数大于0［38‑39］。

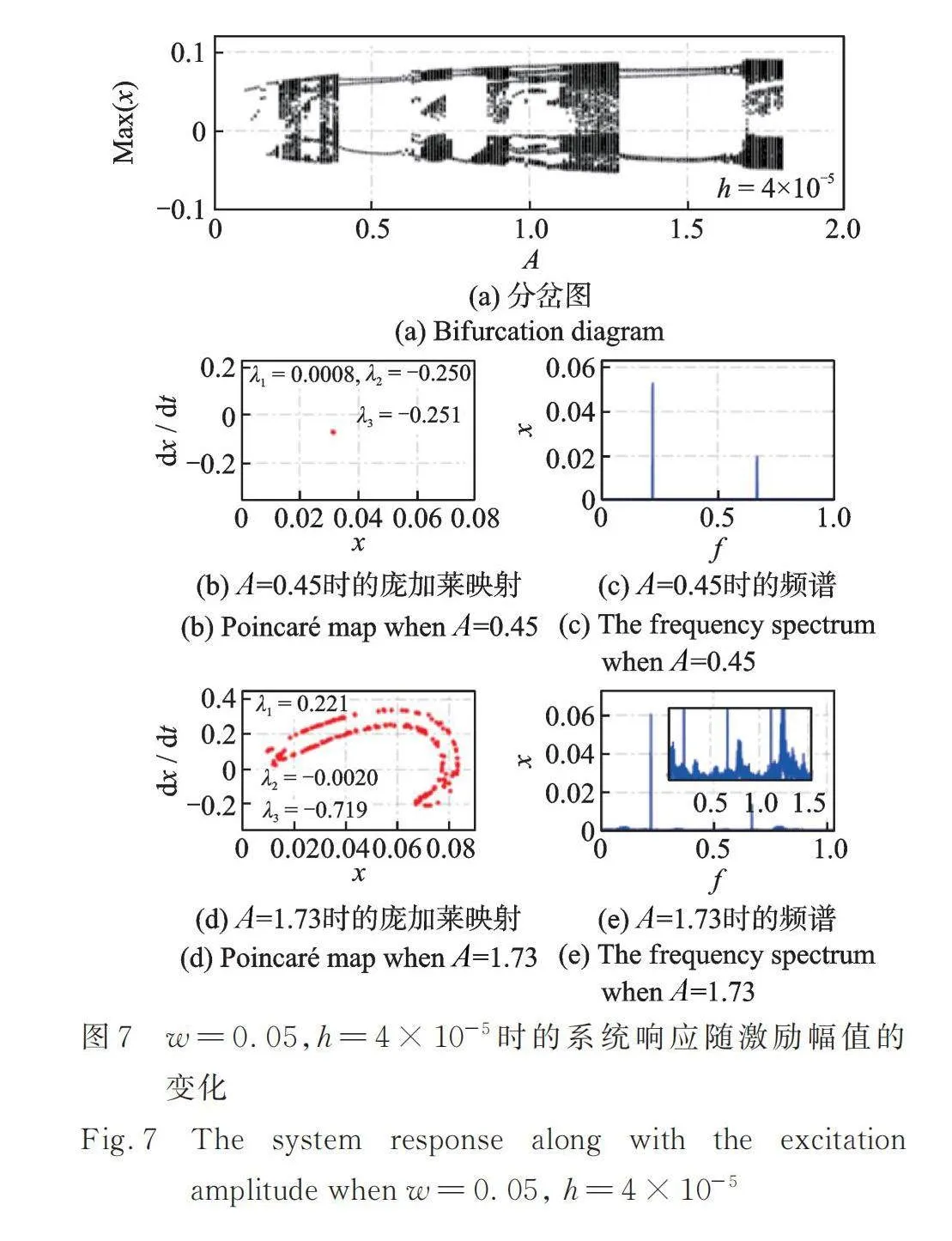
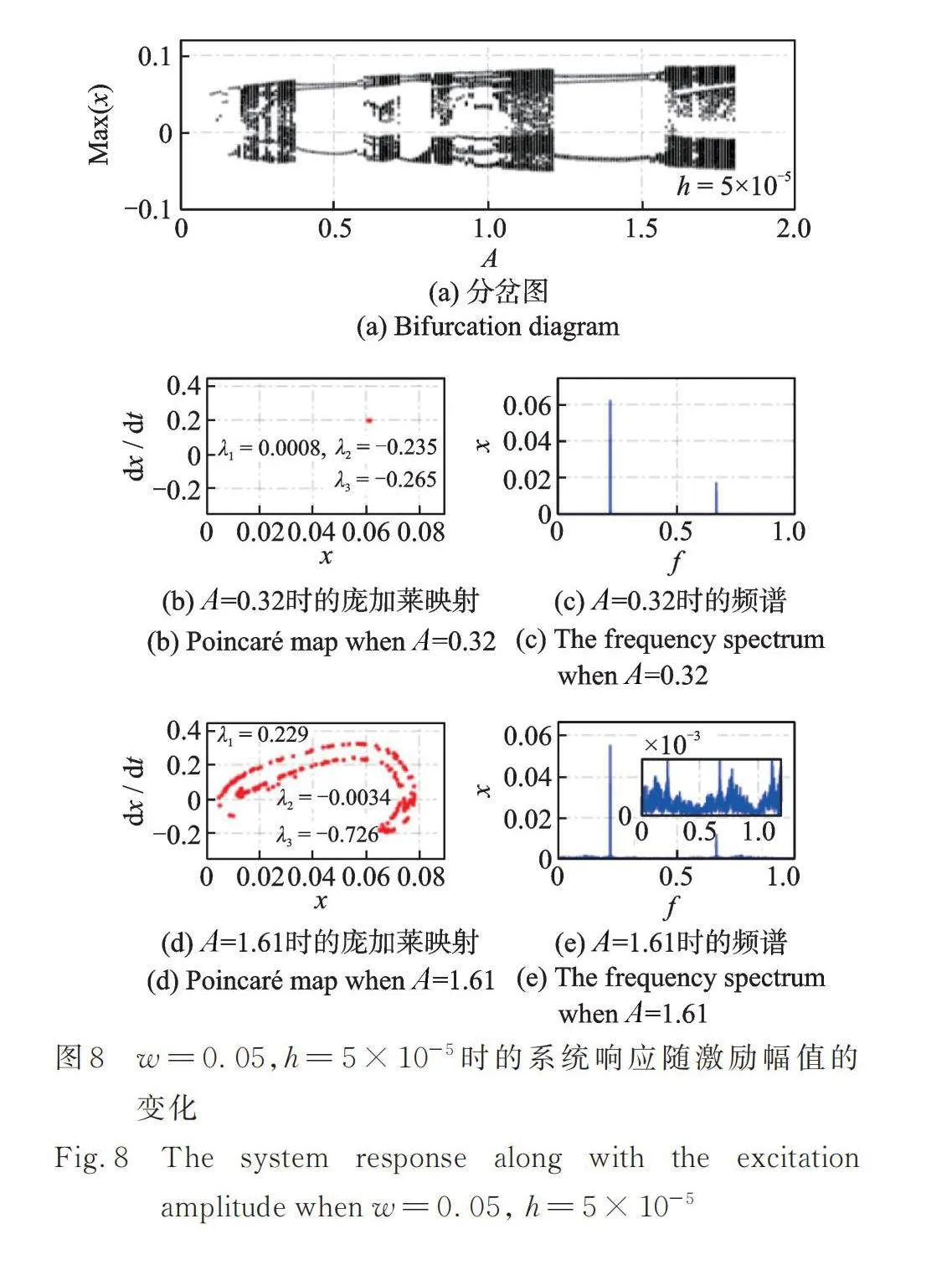
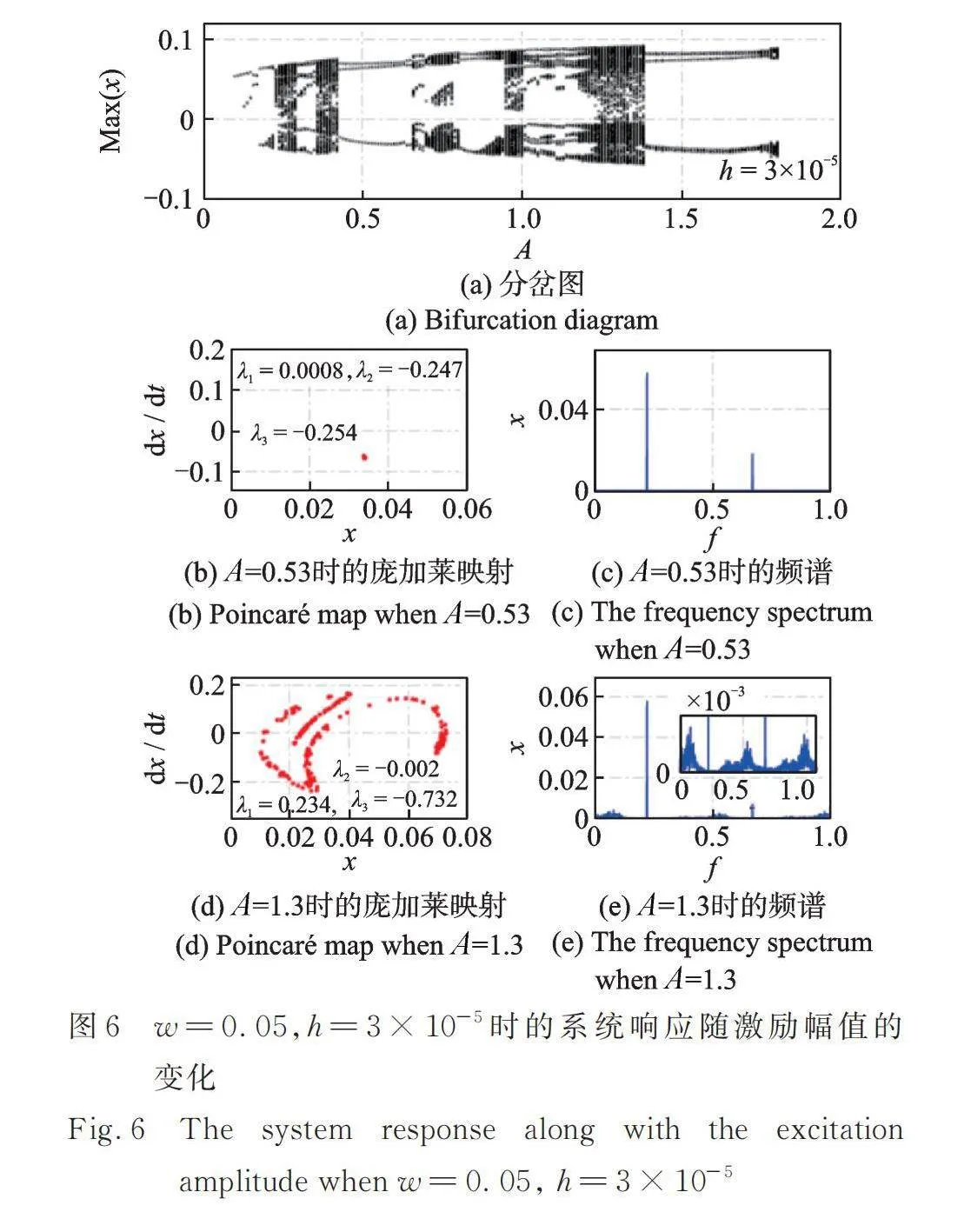
2.2 势阱高度对系统响应的影响

图6～8展示了当势阱宽度时，不同势阱高度下非线性俘能系统响应随激励幅值的变化。同样地，在取固定的激励幅值时，其对应的庞加莱映射、频谱图以及李雅普诺夫指数均能够证明系统是周期响应或是混沌响应，进一步说明了分岔图的准确性。此外，从图中可知，在保证势阱宽度不变的条件下增大势阱高度，在分岔图中体现的混沌区域将会整体朝着激励幅值减小的方向移动。在高激励幅值处的混沌区域将会增大。

3 在故障诊断中的应用

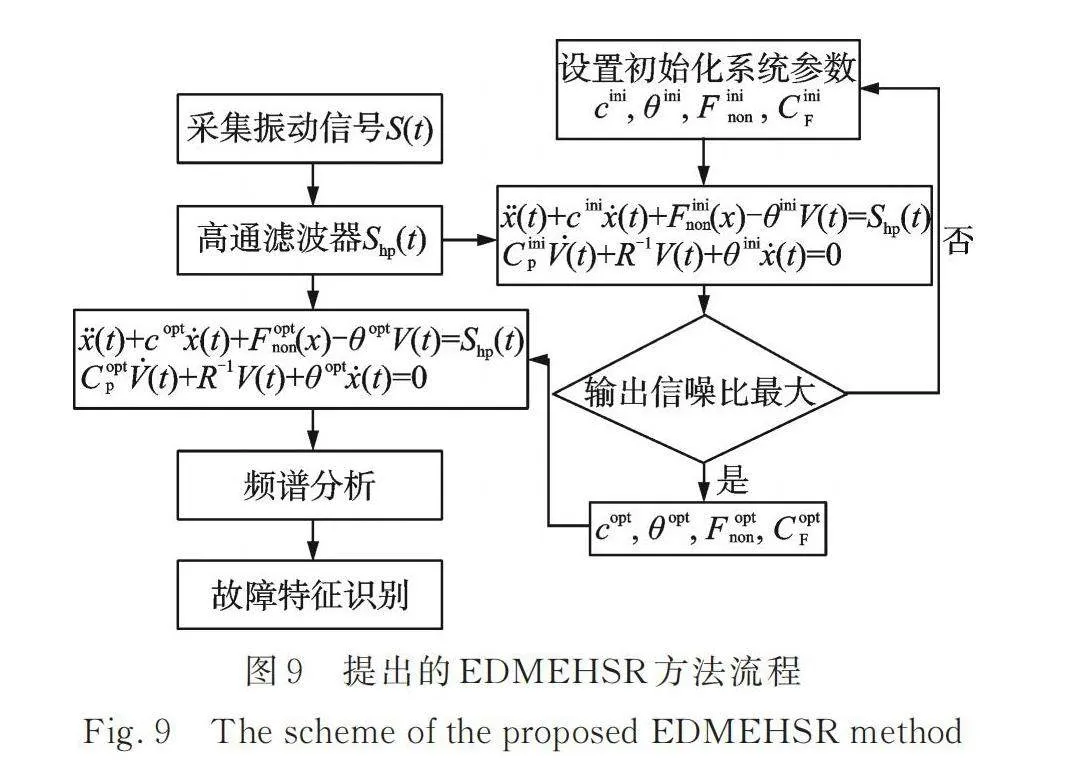
非线性系统的随机共振现象已成功应用于增强俘能系统的输出性能［27‑29］，本节探索机电耦合动力学模型俘能系统的随机共振现象（Stochastic Resonance Phenomenon of the Electromechanical Dynamic Model of the Energy Harvester，EDMEHSR）在故障诊断领域中的应用。如图9所示，EDMEHSR方法的主要流程为：步骤1，获得采集信号的包络信号；步骤2，对包络信号进行高通滤波（去除低频成分）；步骤3，输入到机电耦合方程（1）和（2），利用龙格‑库塔方法获得输出信号；步骤4，计算输出信噪比；步骤5，重复步骤1～4，记录输出信噪比最大时的系统参数以及输出信号。

3.1 仿真验证

为了验证提出的EDMEHSR方法的有效性，将其应用到仿真的轴承内圈和轴承外圈故障信号中。仿真信号模型如下式所示［40］：

（6）

式中 第一项表示周期成分，第二项表示随机脉冲成分，第三项表示干扰谐波成分，第四项表示加性白噪声。可表示为：

（7）

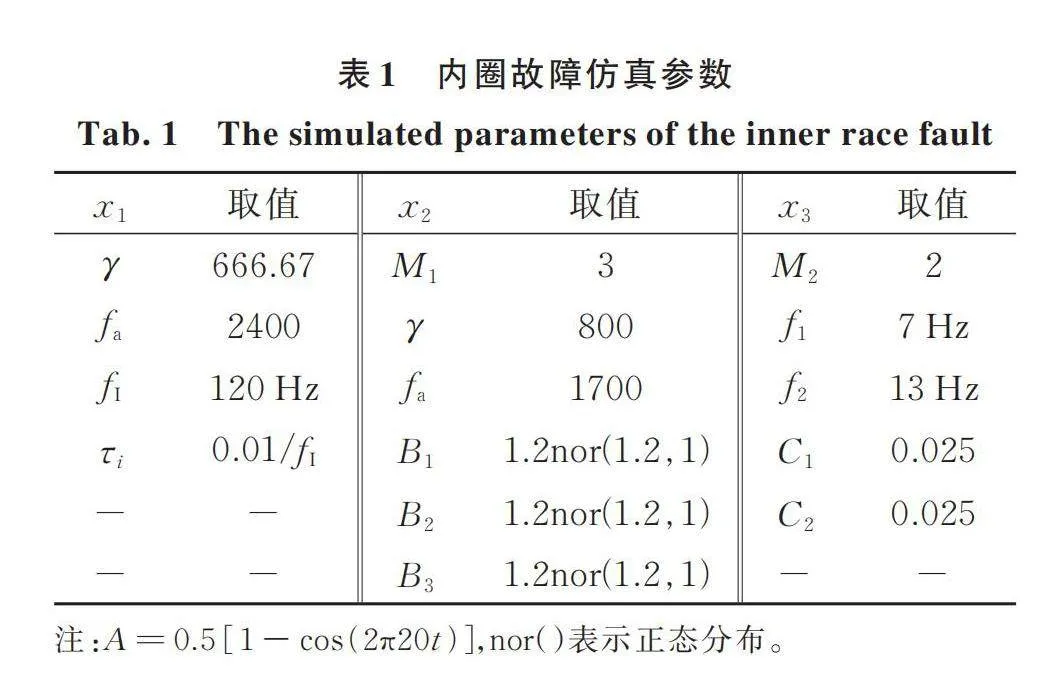
仿真参数如表1和2所示，仿真的轴承外圈故障频率（Ball Pass Frequency of Outer Race，）为73Hz，内圈故障频率（Ball Pass Frequency of Inner Race，）为120 Hz。

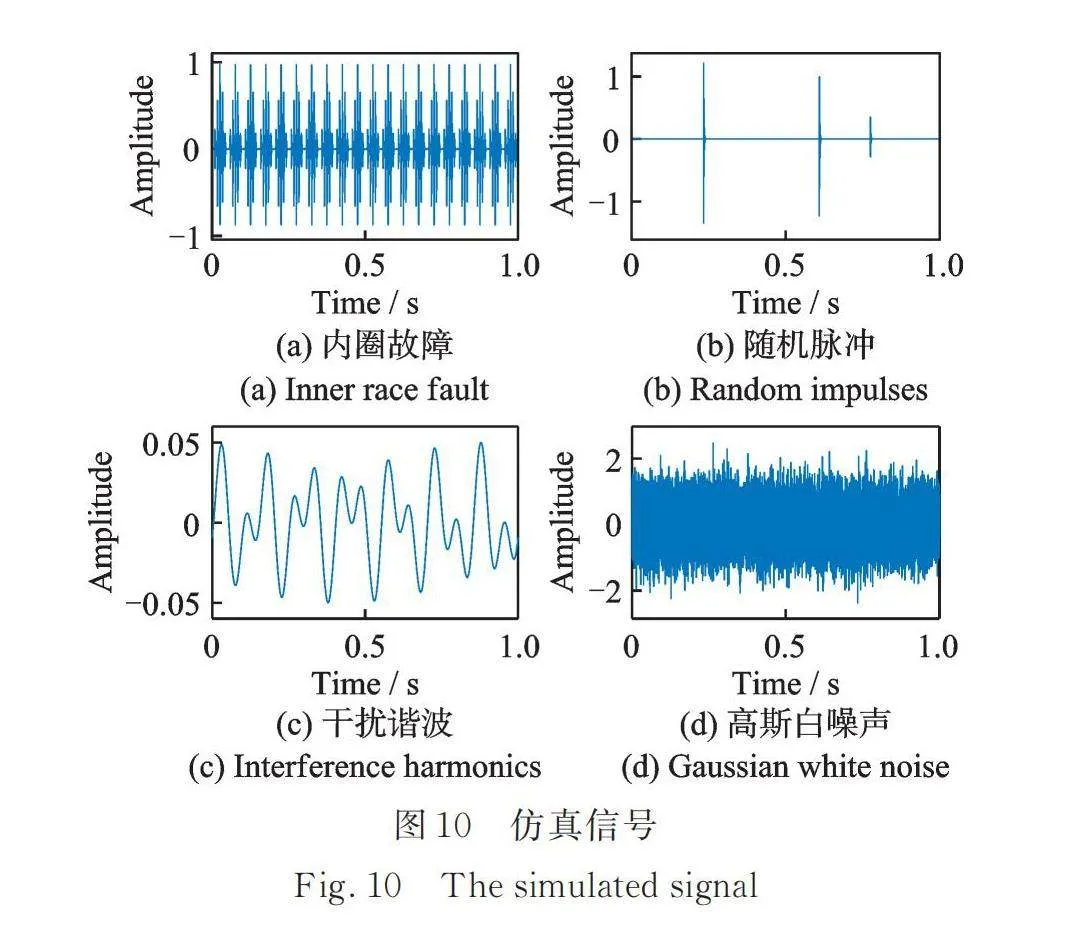
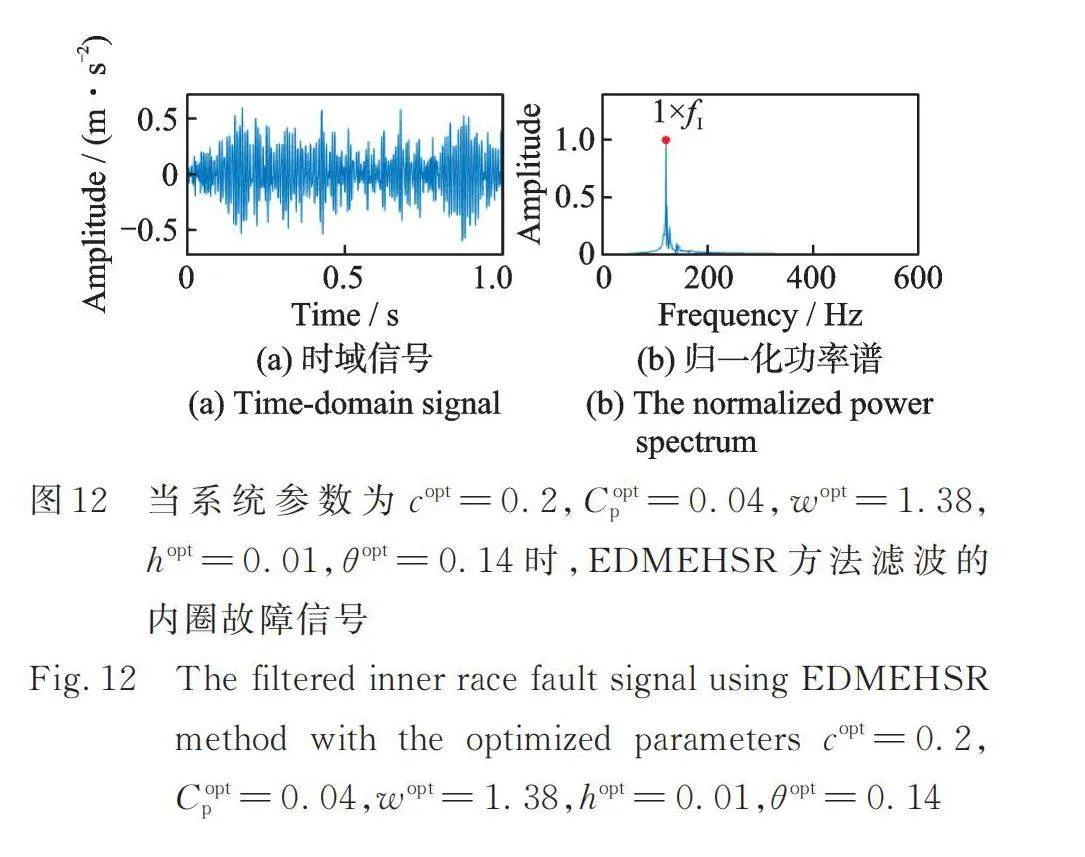
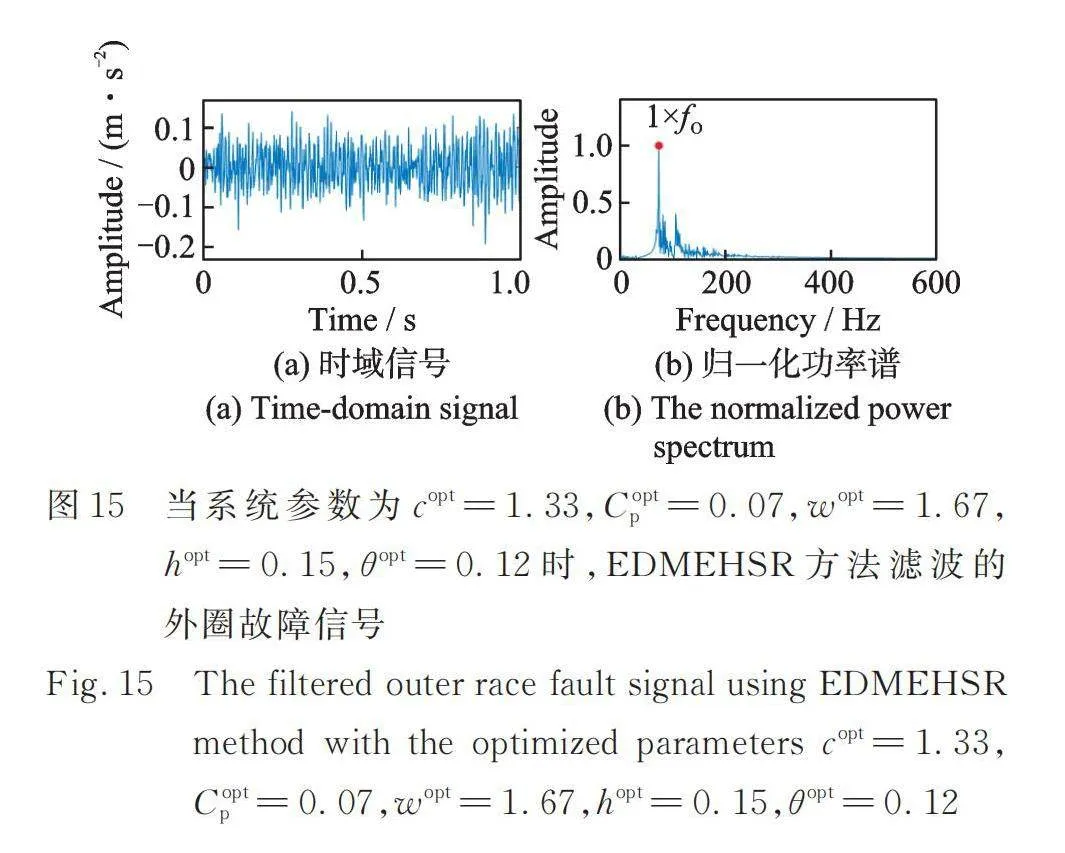
如图10与13所示，仿真的信号成分分别为内圈、外圈的周期脉冲信号、随机脉冲、干扰谐波以及高斯白噪声。仿真内圈混合信号及其归一化包络谱和仿真的外圈混合信号及其归一化包络谱分别如图11和14所示。在其对应的归一化包络谱中，故障特征频率处的幅值受噪声影响很大。应用EDMEHSR方法后（如图12与15所示），仿真的故障特征频率处的幅值得到增强，远远大于其他频率处的幅值。图11，12，14和15频谱对应的信噪比如表3所示，基于EDMEHSR方法可获得最高的信噪比输出信号。综上，这两个仿真案例有效证明了EDMEHSR方法的有效性和其增强目标信号的能力。

3.2 实验验证

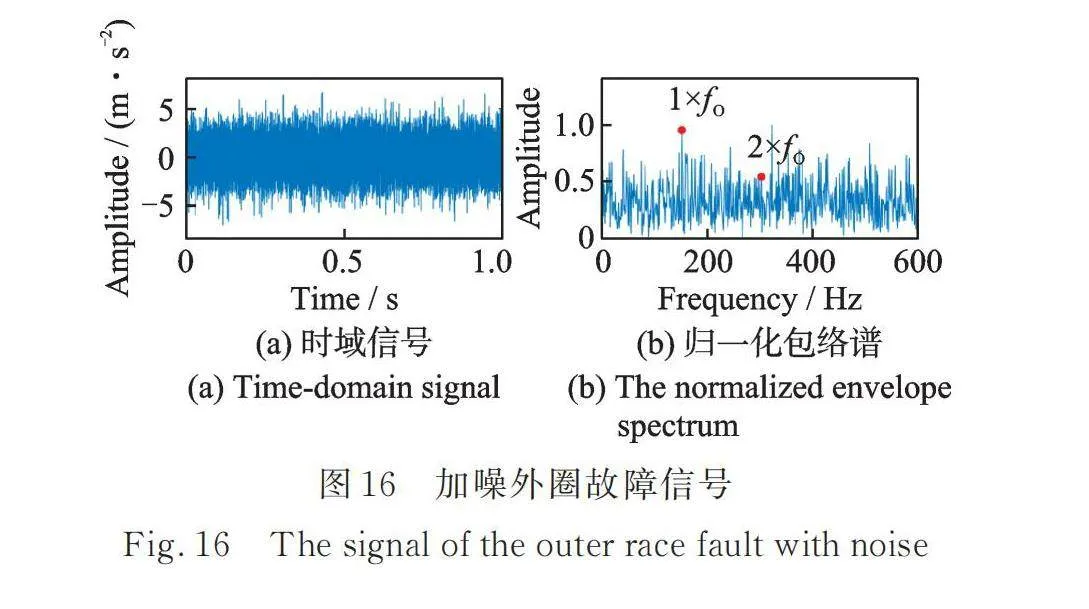
本节利用轴承外圈故障实验数据进一步验证本文提出的EDMEHSR方法的有效性。图16展示了加噪的轴承外圈故障实验信号及其归一化包络谱。图16（b）对应的SNR为-33.9489 dB，且从图中可观测到外圈故障特征频率的峰值几乎被噪声成分淹没。图17展示了利用优化参数的EDMEHSR方法获得的滤波信号及其归一化功率谱，优化参数为：，，，，。图17（b）对应的SNR为-15.3597 dB，且从图中可明显观测到外圈故障特征频率，指示轴承的外圈发生故障。此外，对比输出信号SNR可知，基于EDMEHSR的方法极大提高了故障特征频率处的信噪比。

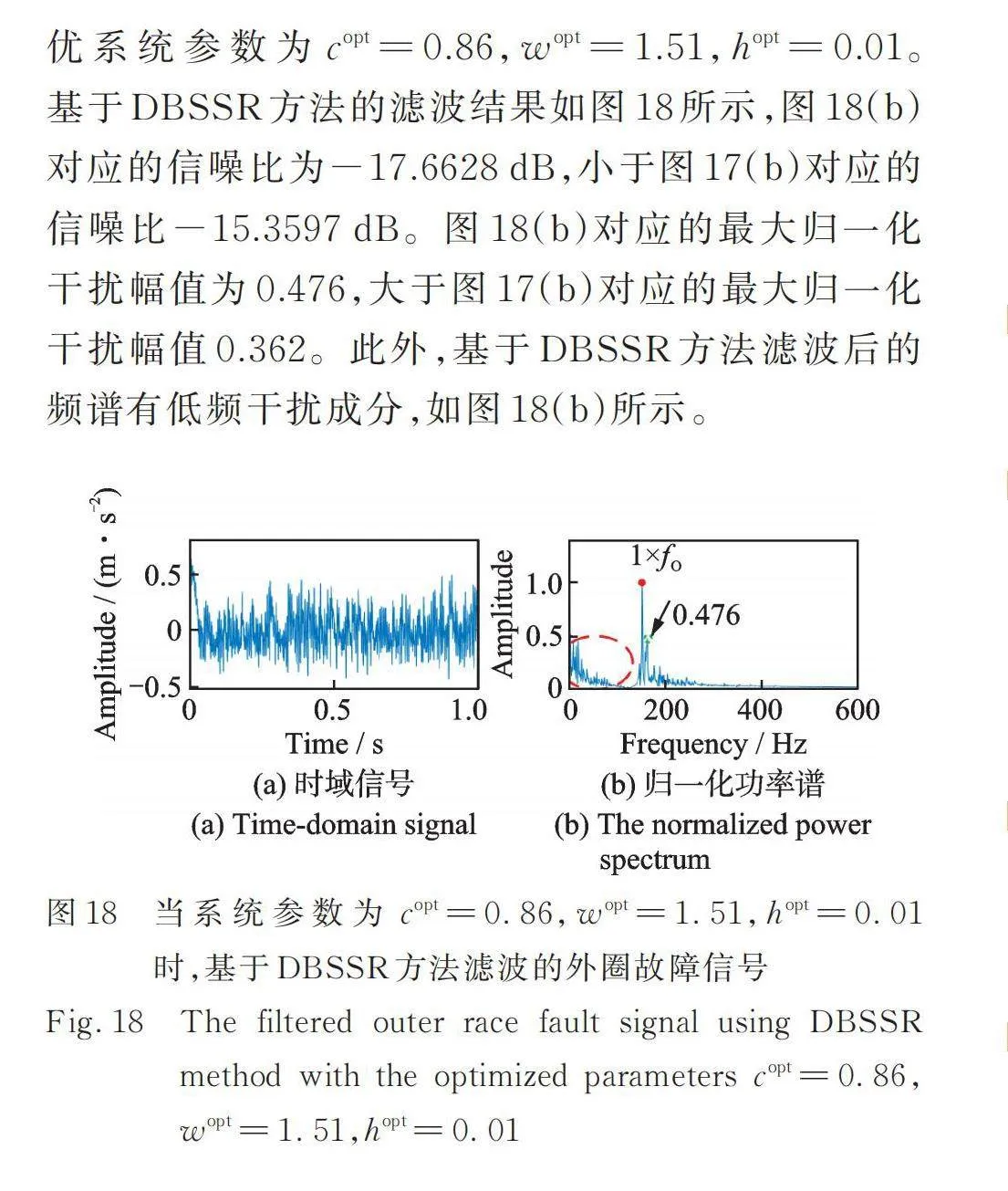
本节还将式（1）对应的解耦双稳态系统（不包含电压项）的随机共振现象（Stochastic Resonance Phenomenon of the Decoupled Bistable System，DBSSR）用于故障诊断，算法流程与图9展示的相同。以信噪比为优化指标，获得DBSSR方法的最优系统参数为，，。基于DBSSR方法的滤波结果如图18所示，图18（b）对应的信噪比为-17.6628 dB，小于图17（b）对应的信噪比-15.3597 dB。图18（b）对应的最大归一化干扰幅值为0.476，大于图17（b）对应的最大归一化干扰幅值0.362。此外，基于DBSSR方法滤波后的频谱有低频干扰成分，如图18（b）所示。

综上，在相同优化流程的情况下，基于机电耦合系统的随机共振现象的故障诊断方法获得的滤波信号具有信噪比高，受干扰小的优点。

4 结 论

本文建立了基于解耦的鞍点退化势能函数的机电耦合动力学模型，数值分析了不同激励幅值下非线性俘能系统的输出响应（周期响应与混沌响应），为非线性俘能系统的结构设计提供参考。最后实现了非线性俘能系统机电耦合动力学模型随机共振现象在故障诊断中的应用。本文主要结论如下：

势阱高度对系统的影响与势阱宽度产生的影响完全相反。增大势阱宽度将使非线性俘能系统发生混沌响应的区域向着大激励幅值方向移动，且在低激励幅值处的混沌区域将会增大。因此在设计具有周期响应特征的非线性俘能系统时，可根据环境激励幅值等级，选取合适的势阱高度与势阱宽度值。

此外，仿真与实验轴承故障案例表明，基于机电耦合动力学模型俘能系统随机共振现象的方法可有效增强故障特征，滤除噪声干扰。这展示了一种非线性能量俘获系统作为非线性滤波器在故障诊断中的潜在工程应用。

参考文献：

［1］杨涛，周生喜，曹庆杰，等. 非线性振动能量俘获技术的若干进展［J］. 力学学报，2021，53（11）： 2894‑2909.

Yang Tao，Zhou Shengxi，Cao Qingjie，et al. Some advances in nonlinear vibration energy harvesting technology［J］. Chinese Journal of Theoretical and Applied Mechanics，2021，53（11）： 2894‑2909.

［2］Zhang Y，Wu X，Lei Y G，et al. Self‑powered wireless condition monitoring for rotating machinery［J］. IEEE Internet Things Journal，2023，11（2）： 3095‑3107.

［3］高鸣源，王平. 磁浮式轨道振动俘能机理与试验研究［J］. 铁道学报，2018，40（6）： 144‑153.

Gao Mingyuan，Wang Ping. Harvesting railroad vibration energy by magnetic levitation oscillation［J］. Journal of the China Railway Society，2018，40（6）： 144‑153.

［4］Cao H，Kong L J，Tang M F，et al. An electromagnetic energy harvester for applications in a high‑speed rail pavement system［J］. International Journal of Mechanical Sciences，2023，243： 108018.

［5］李支援，吕文博，马小青，等. 一种磁力滑动式翼型颤振能量俘获器［J］. 力学学报，2023，55（10）： 2146‑2155.

Li Zhiyuan，Lü Wenbo，Ma Xiaoqing，et al. A magnetic sliding airfoil flutter energy harvester［J］. Chinese Journal of Theoretical and Applied Mechanics，2023，55（10）： 2146‑2155.

［6］Wang J L，Zhou S X，Zhang Z E，et al. High-performance piezoelectric wind energy harvester with Y-shaped attachments［J］. Energy Conversion and Management，2019，181： 645‑652.

［7］Xie X D，Wang Q. A study on an ocean wave energy harvester made of a composite piezoelectric buoy structure［J］. Composite Structures，2017，178： 447‑454.

［8］Liu R W，He L P，Liu X J，et al. A review of collecting ocean wave energy based on piezoelectric energy harvester［J］. Sustainable Energy Technologies and Assessments，2023，59： 103417.

［9］Mitcheson P D，Yeatman E M，Rao G K，et al. Energy harvesting from human and machine motion for wireless electronic devices［J］. Proceedings of the IEEE，2008，96（9）： 1457‑1486.

［10］Yang Z B，Zhou S X，Zu J，et al. High‑performance piezoelectric energy harvesters and their applications［J］. Joule，2018，2（4）： 642‑697.

［11］Zhou S X，Zuo L. Nonlinear dynamic analysis of asymmetric tristable energy harvesters for enhanced energy harvesting［J］. Communications in Nonlinear Science and Numerical Simulation，2018，61： 271‑284.

［12］Huang D M，Han J L，Zhou S X，et al. Stochastic and deterministic responses of an asymmetric quad‑stable energy harvester［J］. Mechanical Systems and Signal Processing，2022，168： 108672.

［13］Tai W C，Zuo L. On optimization of energy harvesting from base‑excited vibration［J］. Journal of Sound and Vibration，2017，411： 47‑59.

［14］Li Z Y，Zhou S Z，Zhang H，et al. Periodic solutions and bifurcations of a tristable flutter‑based energy harvester［J］. Aerospace Science and Technology，2024，144： 108815.

［15］Huang D M，Han J L，Li W，et al. Responses，optimization and prediction of energy harvesters under galloping and base excitations［J］. Communications in Nonlinear Science and Numerical Simulation，2023，119： 107086.

［16］Hou C W，Li C H，Shan X B，et al. A broadband piezo‑electromagnetic hybrid energy harvester under combined vortex‑induced and base excitations［J］. Mechanical Systems and Signal Processing，2022，171： 108963.

［17］Mei X T，Zhou S X，Yang Z C，et al. Enhancing energy harvesting in low‑frequency rotational motion by a quad‑stable energy harvester with time‑varying potential wells［J］. Mechanical Systems and Signal Processing，2021，148： 107167.

［18］Wang J X，Su W B，Li J C，et al. A rotational piezoelectric energy harvester based on trapezoid beam： simulation and experiment［J］. Renewable Energy，2022，184： 619‑626.

［19］Fang S T，Chen K Y，Lai Z H，et al. Analysis and experiment of auxetic centrifugal softening impact energy harvesting from ultra‑low‑frequency rotational excitations［J］. Applied Energy，2023，331： 120355.

［20］靳艳飞，许鹏飞，李永歌，等. 多稳态动力系统中随机共振的研究进展［J］. 力学进展，2023，53（2）： 357‑394.

Jin Yanfei，Xu Pengfei，Li Yongge，et al. Stochastic resonance of multi‑stable dynamical systems： a review［J］. Advances in Mechanics，2023，53（2）： 357‑394.

［21］Kojima N，Lamsal B，Matsumoto N. An adaptive tuning stochastic resonance approach for image enhancement on illumination variant images［J］. Journal of the Institute of Industrial Applications Engineers，2017，5（1）： 24‑31.

［22］Jiao S B，Shi J Q，Wang Y，et al. A novel image noise reduction method for composite multistable stochastic resonance systems［J］. Heliyon，2023，9（3）： e14431.

［23］McInnes C R，Gorman D G，Cartmell M P. Enhanced vibrational energy harvesting using nonlinear stochastic resonance［J］. Journal of Sound and Vibration，2008，318（4‑5）： 655‑662.

［24］Zhang Y S，Zheng R C，Shimono K，et al. Effectiveness testing of a piezoelectric energy harvester for an automobile wheel using stochastic resonance［J］. Sensors，2016，16（10）： 1727.

［25］Xu H T，Zhou S X. Periodicity‑assist double delay-controlled stochastic resonance for the fault detection of bearings［J］. Measurement，2024，225： 114018.

［26］Xu H T，Zhou S X，Yang T. Stochastic resonance of a high‑order‑degradation bistable system and its application in fault diagnosis with variable speed condition［J］. Mechanical Systems and Signal Processing，2023，186： 109852.

［27］Kim H，Tai W，Parker J，et al. Self‑tuning stochastic resonance energy harvesting for rotating systems under modulated noise and its application to smart tires［J］. Mechanical Systems and Signal Processing，2019，122： 769‑785.

［28］Gong X L，Xu P F，Liu D，et al. Stochastic resonance of multi‑stable energy harvesting system with high‑order stiffness from rotational environment［J］. Chaos，Solitons and Fractals，2023，172： 113534.

［29］Shi P M，Liu Z X，Li M D，et al. Nonlinear dynamics analysis of enhancing energy harvesting from intense vibration based on improved asymmetric bistable stochastic resonance model［J］. Chinese Journal of Physics，2023，90：223‑236.

［30］Lai Z H，Leng Y G. Weak‑signal detection based on the stochastic resonance of bistable Duffing oscillator and its application in incipient fault diagnosis［J］. Mechanical Systems and Signal Processing，2016，81： 60‑74.

［31］Lei Y G，Qiao Z J，Xu X F，et al. An underdamped stochastic resonance method with stable‑state matching for incipient fault diagnosis of rolling element bearings［J］. Mechanical Systems and Signal Processing，2017，94： 148‑164.

［32］张刚，徐浩，张天骐. 二维双阱势系统随机共振机理研究及应用［J］. 振动与冲击，2021，40（12）： 15‑22.

Zhang Gang，Xu Hao，Zhang Tianqi. A study and application of stochastic resonance mechanism in a two-dimensional bistable potential system［J］. Journal of Vibration and Shock，2021，40（12）： 15‑22.

［33］贺利芳，刘秋玲，张刚. 高斯势分段双稳随机共振在不同噪声下的轴承故障诊断［J］. 振动与冲击，2023，42（3）： 30‑42.

He Lifang，Liu Qiuling，Zhang Gang. Bearing fault diagnosis under different noises with GPPBSR system［J］. Journal of Vibration and Shock，2023，42（3）： 30‑42.

［34］Yang T，Xu H T，Tang J，et al. Exploring nonlinear degradation benefit of bio‑inspired oscillator for engineering applications［J］. Applied Mathematical Modelling，2023，119： 736‑762.

［35］Zhou S X，Cao J Y，Lin J. Theoretical analysis and experimental verification for improving energy harvesting performance of nonlinear monostable energy harvesters［J］. Nonlinear Dynamics，2016，86（3）： 1599‑1611.

［36］Moysis L，Lawnik M，Volos C. Density‑colored bifurcation diagrams‒a complementary tool for chaotic map analysis［J］. International Journal of Bifurcation and Chaos，2023，33（15）： 2330036.

［37］Moysis L，Giakoumis A，Gupta M K，et al. Observers for rectangular descriptor systems with output nonlinearities： application to secure communications and microcontroller implementation［J］. International Journal of Dynamics and Control，2021，9（2）： 530‑540.

［38］李海涛，丁虎，陈立群. 带有非对称势能阱特性的双稳态能量采集系统混沌动力学分析［J］. 振动与冲击，2020，39（18）： 54‑59.

Li Haitao，Ding Hu，Chen Liqun. Chaotic dynamics of a bi‑stable energy harvesting system with asymmetric potential well characteristics［J］. Journal of Vibration and Shock，2020，39（18）： 54‑59.

［39］Li H，Shen Y J，Han Y J，et al. Determining Lyapunov exponents of fractional‑order systems： a general method based on memory principle［J］. Chaos，Solitons and Fractals，2023，168： 113167.

［40］Miao Y H，Zhao M，Lin J，et al. Application of an improved maximum correlated kurtosis deconvolution method for fault diagnosis of rolling element bearings［J］. Mechanical Systems and Signal Processing，2017，92： 173‑195.

Analysis and fault diagnosis application of the electromechanical dynamic model of the nonlinear energy harvester

XU Hai‑tao，ZHOU Sheng‑xi

（School of Aeronautics，Northwestern Polytechnical University，Xi’an 710072，China）

Abstract： The study of the influence of potential well parameters on the output of a nonlinear energy harvester system is conducive to the design of the high-performance energy harvester system. Meanwhile，the stochastic resonance phenomenon in the corresponding electromechanical coupling dynamics model of the energy harvester system can be used to enhance the characteristics of weak faults，so as to effectively identify weak faults. This paper proposes a decoupled saddle-point-degradation bistable potential function，and the electromechanical dynamic model is introduced. The bifurcation diagram under different excitation amplitudes is obtained to discuss the effect of the barrier width and the barrier height on the responses （periodic response and chaotic response）. According to the methods of the Poincaré map，the frequency spectrum analysis，and the Lyapunov exponent，the periodic response and the chaotic response are examined at a fixed excitation amplitude，which is consistent with that obtained from the bifurcation diagram. Based on the electromechanical dynamic model perturbed by the random noise，the stochastic-resonance-based method is proposed for fault diagnosis，which achieves the enhancement of the simulated and experimental bearing fault characteristics.

Key words： nonlinear system；energy harvesting；fault diagnosis；Lyapunov exponent；Poincaré map

作者简介： 徐海涛（1993―），男，博士研究生。E‑mail： xuhaitao@mail.nwpu.edu.cn。

通讯作者： 周生喜（1987―），男，博士，教授。E‑mail： zhoushengxi@nwpu.edu.cn。