基于状态/参数交替优化估计的齿轮时变啮合刚度辨识方法研究

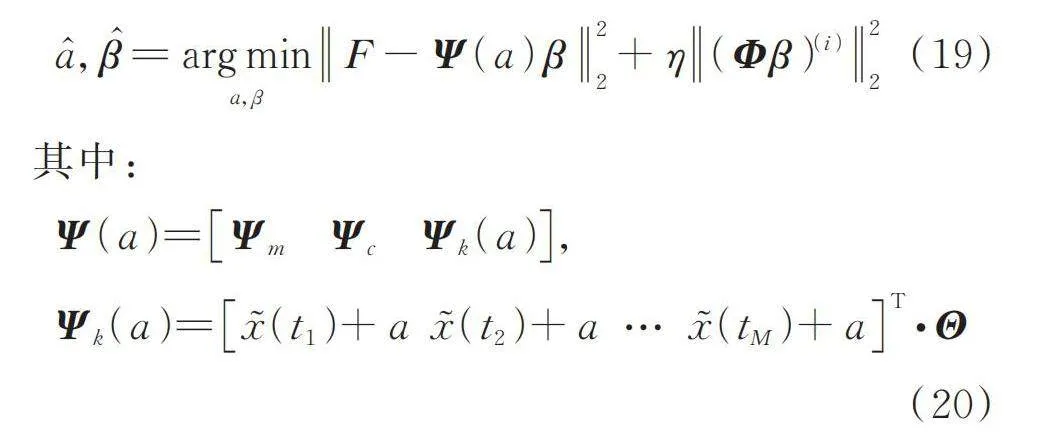
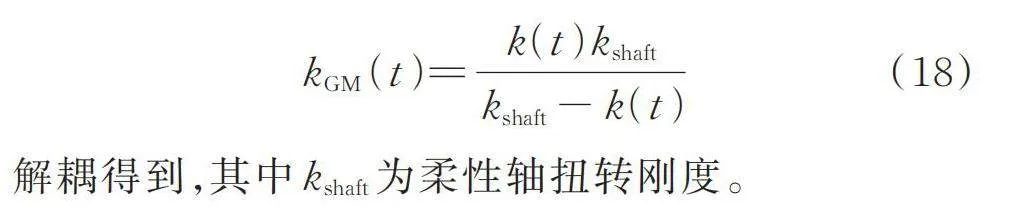
摘要： 齿轮副啮合刚度是齿轮传动动力学模型中的重要参数，啮合刚度识别对于齿轮传动系统振动与噪声的分析以及状态监测具有重要意义。由于齿轮传动系统的时变啮合刚度很难用直接测量的方法得到，因此有必要发展基于数据驱动的齿轮时变啮合刚度辨识方法。为了解决该难题，本文提出了一种系统状态和模型参数交替优化方法以辨识齿轮传动系统时变啮合刚度。该方法以齿轮啮合频率为基频构造傅里叶基函数库表征齿轮时变啮合刚度，并进一步提出了一种基于再生核希尔伯特空间的降噪方法来估计系统状态和模型参数。系统状态变量与时变啮合刚度在动力学模型与数据双重约束下进行交替迭代优化，实现对齿轮传动系统时变啮合刚度的辨识。齿轮传动动力学仿真和齿轮传动系统实验结果验证了所提齿轮时变啮合刚度辨识方法的有效性。

关键词： 参数辨识； 齿轮传动系统； 时变啮合刚度； 交替优化

中图分类号： O327； TH113.1； TH132.41 文献标志码： A 文章编号： 1004-4523（2024）10-1707-07

DOI：10.16385/j.cnki.issn.1004-4523.2024.10.008

引 言

齿轮结构被广泛应用于机械传动系统。在齿轮动力学模型中，时变啮合刚度是反映齿轮系统动态特性的重要参数，其数值变化可导致机械传动系统产生振动和噪声。对齿轮副啮合刚度进行建模与识别，有助于齿轮传动系统的优化设计和状态监测［1⁃5］。

确定齿轮副时变啮合刚度的方法可分为两种：数值计算［6⁃8］和实验辨识［9⁃11］。齿轮啮合刚度数值计算方法主要包括解析法、有限元法和混合法。解析法基于材料力学原理对齿轮啮合刚度进行数学建模，如势能法［12］和石川法［13］。有限元法则在计算中综合考虑了齿轮几何结构、轮齿缺陷、材料性能等多种因素的影响。HU等［14］构建了含有齿隙的有限元模型，并研究了轮齿修形对啮合刚度的影响。与解析法相比，有限元法在复杂齿轮结构仿真中具有更高的计算精度，但其计算时间随着有限元模型的网格细化而大幅增加。为减少有限元法的计算量并保持其高计算精度，混合法（解析⁃有限元法）被用以替代有限元法计算齿轮的离散啮合刚度。在混合法中，齿轮副结构的整体变形由有限元法计算得到，而轮齿接触区的局部变形由解析法确定。CHANG等［15］通过解析赫兹解推导齿轮副的局部接触变形，有效避免了所构建有限元模型对轮齿接触区域的过度细化。CHEN等［16］在轮齿接触点附近构建了局部刚性区以避免模型的局部畸变，并利用所构建的解析⁃有限元混合模型分析了不同裂纹扩展路径对啮合刚度的影响。实验辨识一般通过编码器或成对加速度传感器预先测量齿轮系统传动误差来估计啮合刚度，也可应用模态分析、光弹性法、数字图像相关法等技术辨识齿轮副啮合刚度。例如RAGHUWANSHI等［11］在全啮合周期内的齿轮副多个啮合点处进行模态分析实验，得到离散的齿轮副啮合刚度估计。

上述数值方法在计算啮合刚度时需要精确的齿轮几何结构先验信息，而模态分析法［11］等实验辨识法则需要多次改变齿轮副啮合角进行密集测试，这为齿轮时变啮合刚度辨识带来了困难。为了解决上述难题，本文提出一种系统状态和模型参数交替优化的辨识方法，该方法可在齿轮结构先验信息缺失的条件下通过系统输入和输出信号辨识齿轮时变啮合刚度，仿真和实验结果验证了该方法的有效性。

1 齿轮时变啮合刚度辨识问题

在齿轮传动系统动力学模型中，齿轮副间的相互作用由齿轮啮合界面描述。典型的齿轮传动动力学模型如图1所示，I为转动惯量，r为基圆半径，θ为旋转角位移，T为扭矩，下标1，2分别表示主、从动轮。通过引入等效质量和传动误差的概念，该模型的动力学方程可表示为：

（1）

其中：

（2）

式中 m为齿轮副等效质量；c和k分别为齿轮副的啮合阻尼与啮合刚度；为啮合力；e为几何传动误差（也称空载传动误差）。

若直接对式（1）所示的齿轮传动系统模型进行啮合刚度辨识，需要预知几何传动误差e。测量几何传动误差要求齿轮系统以极低的转速与扭矩（近似空载，扭矩大小仅使齿轮副在整个啮合周期恰好保持接触）运转，从而避免系统动态特性和齿轮副弹性变形的影响。然而，齿轮副在低转速下的运行平稳性往往并不理想，不利于载荷的有效加载和几何传动误差的测量。考虑到低速测量的实际缺陷，本文的输入、输出信号在中高转速下获得：齿轮系统分别在两次不同的扭矩输入下运行，则与两啮合力（fa ，fb）相对应的动力学方程可表示为：

（3）

（4）

将式（3）与式（4）作差，可得：

（5）

式中 状态变量表示两个不同扭矩下的动态传动误差（Dynamic Transmission Error，DTE）测量值之差。系统输入表示对应啮合力之差。DTE定义为。

值得注意的是，式（5）对应的啮合刚度辨识问题不再需要预知几何传动误差e，有效避免了低速空载（或低速轻载）的严苛测量条件。

2 齿轮系统状态及参数交替优化

啮合刚度是齿轮动力学模型中的时变参数，其数值随着传动过程中啮合点的移动而变化。啮合刚度曲线与轮齿的几何形态及齿轮副的啮合状态密切相关，可以反映齿轮系统的动力学行为。为从系统输入、输出信号中辨识啮合刚度，本节提出了一种状态/参数交替优化方法以辨识齿轮时变啮合刚度。

2.1 时变啮合刚度辨识方法

为辨识齿轮传动系统时变啮合刚度，以啮合频率为基频构建傅里叶基函数库，用来表征齿轮副的时变啮合刚度与啮合阻尼：

（6）

假设有M个采样点，为辨识系统参数，根据方程（5），可采用最小二乘法估计回归系数：

（7）

其中：

（8）

然而，最小二乘法容易产生过拟合，为了克服这一缺陷，引入正则项优化参数估计：

（9）

式中 ，为对时间的第i阶导数。为得到啮合刚度曲线的平滑估计，本文将i取为2。超参数可通过交叉验证法［17］确定，并采用自适应矩估计（Adaptive Moment Estimation，ADAM）方法［18］求解优化问题。

相应地，齿轮系统的参数估计可表示为：

（10）

啮合刚度辨识需要传动误差数据及其第一、第二阶时间导数（）。若仅传动误差可测，则可通过对序列的差分计算近似得到。然而，测量过程的噪声信号将在差分运算中被大幅放大，从而降低啮合刚度的辨识精度。

为了降低噪声干扰，本文提出一种基于再生核希尔伯特空间（Reproducing Kernel Hilbert Space，RKHS）［19⁃20］的降噪方法，用于处理含有噪声的质量项及阻尼耦合项（）：

（11）

式中 为RKHS正则项；γ为权重系数；Z由再生核希尔伯特空间映射得到。

式（11）所示优化问题的解可表示为：

（12）

式中 为Gram矩阵，向量为质量及阻尼耦合项（）在再生核希尔伯特空间的映射：

（13）

式中 单位矩阵的维度为。得益于高斯核的通用性和简洁性，本文选取高斯核来构建矩阵G：

（14）

式中 σ为高斯核函数的标准偏差。

然后，基于RKHS的降噪方法被进一步应用于估计系统状态参数：

（15）

其中：

（16）

在式（16）对应的目标函数中，第一项J1确保了系统状态的平滑性，第二项J2限制了传动误差估计值与其测量值间的偏离；，为权重系数。

然后，回归系数的估计值更新为：

（17）

可按式（10）更新啮合刚度的估计值。

将式（13）中的数据替换为优化后的进行估计，再通过式（12）更新系统质量与阻尼项的组合估计。进一步地，通过式（15）和（16）更新系统的状态估计。最后，通过式（10）和（17）相应地更新啮合刚度估计。交替更新系统的状态与参数估计直至收敛或达到更新次数上限。

2.2 时变啮合刚度辨识流程

齿轮系统状态和模型参数具体迭代更新流程如图2所示。

步骤1：测量并记录齿轮副在两次不同输入扭矩下的转角qIkb9Fl8gma2tat0HB1qwg==及扭矩信号。通过式（9）初始化回归系数，通过式（10）确定啮合刚度的初始估计。

步骤2：交替优化系统状态及参数。

步骤2.1：通过式（12）和（13）估计质量及阻尼耦合项Z；

步骤2.2：通过式（15）和（16）估计传动误差x；

步骤2.3：通过式（10）和（17）重新估计啮合刚度k；

步骤2.4：用更新后的传动误差及啮合刚度估计构造替换式（13）中的。

步骤3：重复步骤2直至Z，k，x估计值的变化量小于设定值或达到迭代次数上限。

3 仿真与实验验证

3.1 仿真算例

为验证所提齿轮时变啮合刚度辨识方法的有效性，采用表1中的参数构建齿轮系统动力学模型（式（1））进行动态仿真。齿轮副啮合刚度的真值由MA等［21］所提解析法计算得到，啮合阻尼依据瑞利阻尼模型按10%阻尼比取值。几何传动误差参考DONG等［22］采用的建模方式，假设其由主、从动轮的跳动误差（偏心）引起，误差参数如表1所示。

依据所提啮合刚度辨识方法，齿轮动力系统的输入扭矩设为10 N·m和30 N·m，输入轴转速为600 r/min。齿轮系统输出的传动误差信号由四阶龙格⁃库塔法计算得到。采样频率为23 kHz，采样时间为10 s。为模拟实际测量环境，输出的传动误差信号按信噪比（Signal⁃to⁃Noise Ratio，SNR） =30，25，20 dB混入高斯白噪声。在回归矩阵中，傅里叶级数的基频（齿轮副啮合频率）为230 Hz，频率最高倍数N设为40。同时，非线性动力学稀疏识别（Sparse Identification of Nonlinear Dynamics，SINDy）方法［23］被用于辨识同一齿轮传动系统的啮合刚度。

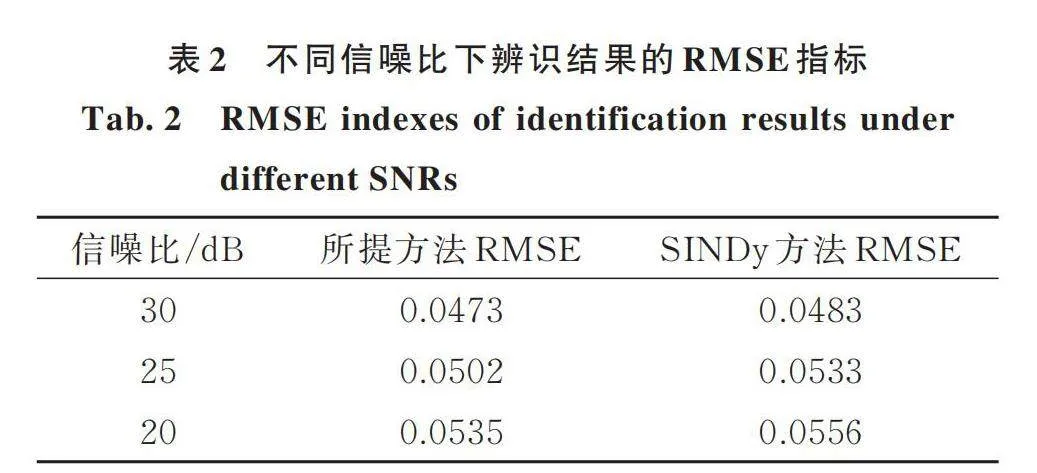
辨识得到的时变啮合刚度曲线及其真值如图3所示。表2为所提方法与SINDy方法在不同信噪比下辨识结果的均方根误差（Root Mean Square Error，RMSE）指标，其定义为刚度估计与其真值间的均方根误差。

识别齿轮系统参数需要同时用到DTE信号及其一阶、二阶导数数据。当仅DTE信号可测时，SINDy方法直接使用对噪声敏感的传动误差信号高阶导数进行刚度估计。与SINDy方法相比，本文方法通过状态信号在再生核希尔伯特空间的映射变换有效削弱噪声影响。此外，本文方法引入了齿轮动力系统的物理模型与测量数据双重约束，在保证所估计刚度曲线和状态曲线平滑性的同时，限制了状态估计与其测量值间的偏差。本节啮合刚度的辨识结果表明，在相同噪声环境下，所提方法相较于SINDy方法具有更高的辨识精度。

3.2 实验验证

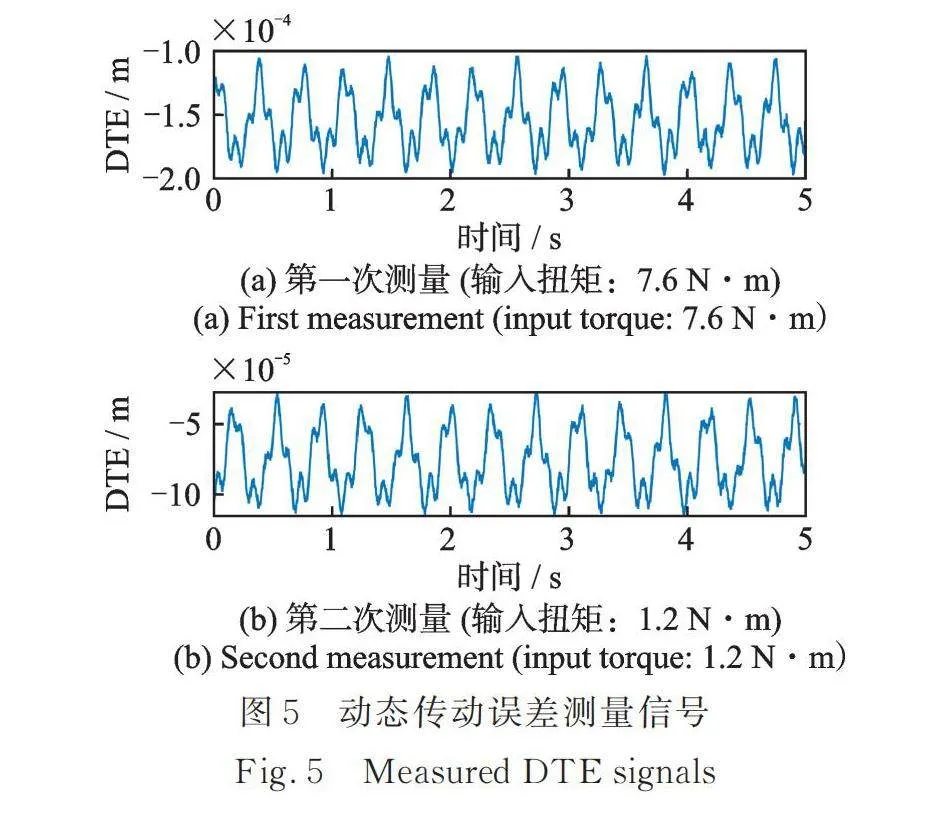
为进一步验证所提啮合刚度辨识方法的有效性，以图4所示的齿轮箱为对象开展实验。安装在输入轴和输出轴端的编码器每转产生1024个脉冲信号。为了简化实验配置，啮合力近似为，其中输入扭矩可由安装在输入轴侧的单个动态扭矩传感器检测得到。在输入扭矩大小分别为7.6 N·m和1.2 N·m的条件下开展测试，输入轴转速为600 r/min。数据采集仪的采样频率为500 kHz，采样时间为5 s。图5为两次不同输入扭矩下动态传动误差信号的测量结果。对两次不同啮合力对应的实测DTE信号按相关性最大化进行对齐，然后计算其差值，得到系统的输出信号x。

齿轮箱参数与仿真中的齿轮副参数（见表1）一致，区别在于齿轮实验台的输入、输出轴是柔性件（因此会参与构成齿轮副的啮合）。相应地，齿轮啮合刚度kGM（t）需要从总刚度估计中按：

（18）

解耦得到，其中为柔性轴扭转刚度。

此外，传动误差信号的直流分量无法通过编码器测量得到。为了确定未知直流分量a，系数向量的初始化过程被改写为：

（19）

其中：

（20）

传动误差信号x被修正为用以估计系统状态及参数。图6所示为采用所提方法和SINDy方法辨识得到的齿轮啮合刚度曲线。作为参考，依照表1所示齿轮箱的先验信息，利用MA等［20］所提解析法计算啮合刚度的理论值。实验结果显示，所提方法辨识的啮合刚度与解析法计算结果的一致性明显优于SINDy方法，表明所提齿轮时变啮合刚度方法具有较高的辨识精度。

4 结 论

本文针对齿轮传动系统时变啮合刚度建模与辨识问题，提出了一种状态/参数交替优化估计方法。首先，为表征啮合刚度时变特性，构建以齿轮啮合频率为基频的傅里叶基函数库来拟合时变刚度，并提出了兼顾齿轮动力系统物理模型约束与刚度曲线平滑性要求的参数初始化方法。进一步地，通过引入物理模型与数据双重约束，实现对系统状态与模型参数的交替优化。同时，状态测量信号的噪声在再生核希尔伯特空间的映射变换中被削减，有效提高了啮合刚度辨识精度。齿轮传动的数值仿真和动态实验验证了所提齿轮时变啮合刚度辨识方法的有效性。需要注意的是，当系统转速较高时，实验测试的采样频率不宜设置得过低，否则会影响对输入、输出轴转角的测量精度，从而降低啮合刚度的辨识精度。

参考文献：

［1］马志赛，丁千，刘莉，等. 线性时变结构模态参数时域辨识方法的研究进展［J］. 机械工程学报，2018，54（23）： 137-159.

MA Zhisai，DING Qian，LIU Li，et al. Research progress on time-domain modal parameter estimation methods for linear time-varying structures［J］. Journal of Mechanical Engineering，2018，54（23）： 137-159.

［2］蔡宇，刘旭，程英豪. 线性变参数振动系统的全局辨识［J］. 机械工程学报，2022，58（23）： 114-122.

CAI Yu，LIU Xu，CHENG Yinghao. Global identification of linear parameter-varying vibration systems［J］. Journal of Mechanical Engineering，2022，58（23）： 114-122.

［3］周国峰，刘博. 某空气舵系统非线性建模及参数识别［J］. 振动工程学报，2023，36（5）： 1216-1222.

ZHOU Guofeng，LIU Bo. Nonlinear modeling and parameter identification of an air rudder system［J］. Journal of Vibration Engineering，2023，36（5）： 1216-1222.

［4］SHI J F，GOU X F，ZHU L Y. Five-state engaging model and dynamics of gear-rotor-bearing system based on time-varying contact analysis considering gear temperature and lubrication［J］. Applied Mathematical Modelling，2022，112： 47-77.

［5］NATALI C，BATTARRA M，DALPIAZ G，et al. A critical review on FE-based methods for mesh stiffness estimation in spur gears［J］. Mechanism and Machine Theory，2021，161： 104319.

［6］CHEN Z G，ZHOU Z W，ZHAI W M，et al. Improved analytical calculation model of spur gear mesh excitations with tooth profile deviations［J］. Mechanism and Machine Theory，2020，149： 103838.

［7］COOLEY C G，LIU C G，DAI X，et al. Gear tooth mesh stiffness： a comparison of calculation approaches［J］. Mechanism and Machine Theory，2016，105： 540-553.

［8］YANG L T，ZENG Q，YANG H S，et al. Dynamic characteristic analysis of spur gear system considering tooth contact state caused by shaft misalignment［J］. Nonlinear Dynamics，2022，109（3）： 1591-1615.

［9］PANDYA Y，PAREY A. Experimental investigation of spur gear tooth mesh stiffness in the presence of crack using photoelasticity technique［J］. Engineering Failure Analysis，2013，34： 488-500.

［10］RAGHUWANSHI N K，PAREY A. Experimental measurement of gear mesh stiffness of cracked spur gear by strain gauge technique［J］. Measurement，2016，86： 266-275.

［11］RAGHUWANSHI N K，PAREY A. A new technique of gear mesh stiffness measurement using experimental modal analysis［J］. Journal of Vibration and Acoustics，2019，141（2）： 021018.

［12］DAI H，LONG X H，CHEN F，et al. An improved analytical model for gear mesh stiffness calculation［J］. Mechanism and Machine Theory，2021，159： 104262.

［13］SHI J L，MA X G，XU C L，et al. Meshing stiffness analysis of gear using the Ishikawa method［J］. Applied Mechanics and Materials，2013，401-403： 203-206.

［14］HU Z H，TANG J Y，ZHONG J，et al. Effects of tooth profile modification on dynamic responses of a high speed gear-rotor-bearing system［J］. Mechanical Systems and Signal Processing，2016，76-77： 294-318.

［15］CHANG L H，LIU G，WU L Y. A robust model for determining the mesh stiffness of cylindrical gears［J］. Mechanism and Machine Theory，2015，87： 93-114.

［16］CHEN K K，HUANGFU Y F，MA H，et al. Calculation of mesh stiffness of spur gears considering complex foundation types and crack propagation paths［J］. Mechanical Systems and Signal Processing，2019，130： 273-292.

［17］ARLOT S，CELISSE A. A survey of cross-validation procedures for model selection［J］. Statistics Surveys，2010，4： 40-79.

［18］KINGMA D P，BA J. ADAM： a method for stochastic optimization［J］. arXiv preprint arXiv：1412.6980，2014.

［19］LIN M M，CHENG C M，PENG Z K，et al. Nonlinear dynamical system identification using the sparse regression and separable least squares methods［J］. Journal of Sound and Vibration，2021，505： 116141.

［20］CHENG C M，ZHAO B X，FU C K，et al. A two-stage sparse algorithm for localization and characterization of local nonlinear structures［J］. Journal of Sound and Vibration，2022，526： 116823.

［21］MA H，ZENG J，FENG R J，et al. An improved analytical method for mesh stiffness calculation of spur gears with tip relief［J］. Mechanism and Machine Theory，2016，98： 64-80.

［22］DONG X J，HUANGFU Y F，YU X L，et al. Identification of the error excitation in gear systems： a mediator algorithm between simulation and experiment［J］. Journal of Sound and Vibration，2024，568： 118060.

［23］BRUNTON S L，PROCTOR J L，KUTZ J N. Discovering governing equations from data by sparse identification of nonlinear dynamical systems［J］. Proceedings of the National Academy of Sciences，2016，113（15）： 3932-3937.

Time-varying mesh stiffness identification of gear systems based on an alternating state/parameter optimization estimation

LIN Miao‑miao1，CHENG Chang-ming1，PENG Zhi‑ke1，2

（1.State Key Laboratory of Mechanical System and Vibration，Shanghai Jiao Tong University，Shanghai 200240，China； 2.School of Mechanical Engineering，Ningxia University，Yinchuan 750021，China）

Abstract： The time-varying mesh stiffness is a core parameter of gear systems，and the mesh stiffness identification is of great significance for the dynamic analysis and condition monitoring of gear transmission systems. Since it is difficult to directly measure the mesh stiffness，it is necessary to develop a data-driven time-varying mesh stiffness identification method. To deal with this problem，an alternating state-parameter optimization method is proposed to identify the time-varying mesh stiffness of gear systems. The Fourier series with the fundamental frequencipayzdxpwuQ7Cwg3lQ1RjA==y of the mesh frequency is constructed to characterize the mesh stiffness. Furthermore，a Reproducing Kernel Hilbert Space （RKHS）-based de-noise method is further proposed to estimate the system state and parameter. The system state and stiffness parameter are alternately optimized with the joint constrains of dynamic model and data to realize the time-varying mesh stiffness identification of gear transmission systems. The simulation and experimental studies validate the effectiveness of the new mesh stiffness identification method for gear systems.

Key words： parameter identification；gear transmission system；time-varying mesh stiffness；alternating optimization

作者简介： 林苗苗（1997―），女，博士研究生。E-mail：linmmiao@sjtu.edu.cn。

通讯作者： 程长明（1987―），男，博士，副教授，博士生导师。电话：（021）34206831-828；E-mail：ccming@sjtu.edu.cn。