非线性结构系统的局部连接刚度辨识方法研究

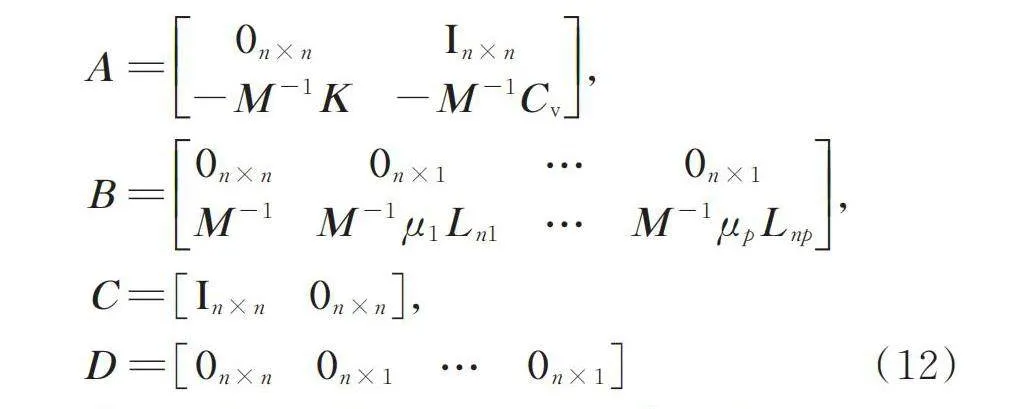
摘要： 连接结构在工程应用领域广泛存在，连接位置处的局部非线性特征对结构系统的动力学建模与特性预示具有重要影响。针对非线性结构系统局部连接参数未知或难以测量的问题，本文从结构动力学反问题的角度出发，提出一种基于频响函数变换的局部线性连接刚度辨识方法，通过与时域非线性子空间辨识方法相结合，可进一步获取非线性结构系统的局部线性和非线性连接刚度。设计并搭建三自由度结构系统的数值算例和实验系统，开展辨识方法的数值和实验验证，结果表明，所提方法能够分离并辨识得到非线性结构系统的标称线性系统频响函数和非线性参数，进而实现局部线性和非线性连接刚度的联合辨识。

关键词： 连接刚度辨识； 连接结构； 非线性系统； 非线性子空间辨识方法

中图分类号： O327；O322 文献标志码： A 文章编号： 1004-4523（2024）10-1698-09

DOI：10.16385/j.cnki.issn.1004-4523.2024.10.007

引 言

在机械、土木、航空航天等工程领域，大型结构系统中广泛存在着各种各样的连接形式，例如螺栓、铆接、焊接、楔环等［1⁃4］。由于加工、装配误差和使用磨损等因素，连接位置不可避免地存在局部非线性特征，给系统的动力学建模与特性预示带来挑战，甚至影响其工作性能，威胁结构的整体运行安全［5⁃7］。针对含局部连接的结构系统动力学问题，一方面需要进行非线性机理研究，探索局部连接的精细化建模方法［8⁃12］；另一方面需要开展数据驱动的局部连接特性辨识，对正向建模中难以精确表征的内部机理进行捕捉，进而准确获取真实工作条件下连接结构系统的动力学特性，是本文的研究重点。

关于系统辨识的研究始于20世纪50年代［13］，早期多以线性系统为研究对象，随着工程应用需求的日益拓展，辨识理论与方法研究不断深入，非线性系统辨识已逐渐成为当前工程应用研究领域的热点问题［14⁃18］。非线性系统辨识方法可分为线性化方法、时域方法、频域方法、时频分析、非线性模态分析、黑箱建模和模型更新等几大类［17⁃20］，近年来已在不同领域的工程结构系统辨识中得以应用，例如螺栓连接结构［21⁃23］、太阳能电池板［24］、卫星结构［25］、飞行器舵面［26⁃29］等，表现出了较大的发展前景。

在众多非线性系统辨识方法中，基于输出反馈思想的辨识方法近年来得到了较多关注。Adams等［30］最先提出输出反馈思想，其核心在于将非线性恢复力视为内部反馈力，令其与外部激励共同作用于标称线性系统以产生原始非线性系统的响应，并发展了基于输出反馈思想的频域非线性系统辨识（NIFO）方法［31］。Marchesiello等［32］基于输出反馈思想提出了时域非线性子空间辨识（Time⁃domain Nonlinear Subspace Identification，TNSI）方法，并应用于机械系统非线性参数辨识。Marchesiello等［33］提出消除辨识模型阶数过估计导致虚假极点的策略，提高了TNSI方法的辨识精度。Zhang等［34］分两步估计标称线性系统频响函数（Frequency Response Function，FRF）和非线性参数，在保证辨识精度的前提下，降低了TNSI方法的计算复杂度。Liu等［35］引入分离策略在不同激励幅值下分别辨识标称线性系统和非线性参数，降低了TNSI方法同步处理线性部分和非线性部分时由于两者数值量级相差较大而引起的耦合误差。Ma等［36］提出了一种仅输出的TNSI方法，在标称线性系统的特征矩阵或状态空间矩阵已知的前提下，只需测量输出数据即可对非线性参数进行辨识。孙玉凯等［29］采用TNSI方法对含间隙非线性的二元翼段进行辨识，得到了标称线性系统和非线性参数，并与条件逆向路径法进行了对比验证。Zhu等［37］引入相似系数和距离函数对标称线性系统的模态信息进行聚类，实现了TNSI方法的自适应模型定阶。

基于输出反馈思想的辨识方法提供了一类重要的非线性系统辨识框架，以TNSI方法为例，通过将非线性恢复力视为内部反馈力，可有效辨识标称线性系统和非线性参数。但需要说明的是，当结构系统某一位置同时存在线性和非线性连接刚度时，TNSI方法会将线性部分的连接参数归入标称线性系统中，导致局部连接参数的辨识结果中仅包含非线性部分，从而与真实情况产生严重偏差。与此同时，这类方法在估计标称线性系统时，可获得其频响函数以及固有频率、阻尼比等模态信息，但不能直观地获取局部连接位置的物理参数。因此，针对很多工程结构系统的局部连接参数未知或难以测量的问题，仍需进一步研究能够准确获取局部连接参数的非线性系统辨识方法，以期为工程连接结构的动力学建模与特性预示提供技术支撑。

综上所述，本文旨在发展非线性结构系统的局部连接刚度辨识方法。首先，利用结构系统刚度矩阵的性质，提出一种基于频响函数变换的局部线性连接刚度辨识方法；其次，将局部线性连接刚度辨识方法与TNSI方法相结合，以实现结构系统局部线性和非线性连接刚度的联合辨识；最后，基于数值算例和振动实验对所提结构系统的局部连接刚度辨识方法进行验证。

1 局部连接刚度辨识方法

1.1 局部线性连接刚度辨识

基于结构动力学方程的一般形式，本节对局部线性连接刚度辨识理论进行推导。对于一个自由度线性时不变结构系统，假设其质量矩阵为，阻尼矩阵为，刚度矩阵为，位移响应为，外激励为，则其动力学方程可用以下微分方程表示：

（1）

将式（1）变换到频域为：

（2）

式中 ；和分别为位移响应和外激励的傅里叶变换。由式（2）可得位移频响函数的表达式为：

（3）

对线性结构系统而言，其频响函数可基于输入⁃输出数据，采用时域线性子空间辨识（Time⁃domain Linear Subspace Identification，TLSI）方法进行估计。如在该结构系统第个自由度与边界之间附加线性连接刚度，则其位移频响函数的表达式为：

（4）

式中 为附加线性连接后的位移频响函数；为结构系统与边界之间附加的线性连接刚度矩阵，其第行第列的元素为，其余元素均为零。

由式（3）和（4）可知，通过位移频响函数逆矩阵做差的方式可求得结构系统与边界之间附加的线性连接刚度矩阵：

（5）

进一步，取矩阵的第行第列的元素即可得到结构系统与边界之间附加的线性连接刚度。当结构系统的响应信号为速度或加速度时，可先计算得到速度或加速度频响函数，再变换得到相应的位移频响函数，具体变换关系为：

（6）

式中 ，和依次为位移、速度和加速度频响函数。为叙述方便，后文仅针对位移频响函数进行讨论。

假设式（3）中结构系统的第个自由度与边界之间原本无线性弹簧连接，则其维刚度矩阵在第列上的元素之和为零：

（7）

式中 为刚度矩阵第列的元素之和。显然，当在结构系统的第个自由度与边界之间附加线性连接刚度后，如式（4）所示，此时新系统的刚度矩阵变为，其第列的元素之和不再为零，而是恰好等于。

将式（4）中频响函数逆矩阵第列元素的实部相加，可得：

（8）

式中 表示频响函数逆矩阵第列元素的实部之和，是一个以频率为自变量的二次曲线，其常数项部分恰好为。由此结合式（7）可知，用形式的二次曲线对进行拟合，取其常数项即可辨识得到局部线性连接刚度。

综上所述，基于频响函数变换的局部线性连接刚度辨识方法可归纳如下：首先采用TLSI方法估计频响函数，其次对频响函数逆矩阵列元素的实部进行求和，最后用形式的二次曲线对求和结果进行拟合，取其常数项即为结构系统与边界之间的局部线性连接刚度。

1.2 局部非线性连接刚度辨识

上一节中的局部线性连接刚度辨识方法不仅适用于线性结构系统，对非线性结构系统的标称线性部分同样适用，但前提是需要首先得到标称线性系统的频响函数。因此，针对非线性结构系统，可采用TNSI方法分离其标称线性系统和非线性参数，在辨识得到非线性参数的同时，获取标称线性系统的频响函数，进而完成局部线性连接刚度的辨识，具体过程如下。

对于非线性结构系统，其动力学方程为：

（9）

式中 非线性恢复力为个分量的总和，其中每个分量取决于表示非线性类型的描述函数；为需要辨识的非线性参数；表示非线性的位置向量。

将式（9）中的非线性恢复力视作内部反馈力，可进行如下变换：

（10）

引入状态向量和输出向量，并将式（10）的右侧视为广义输入向量，则式（10）可改写为如下状态空间模型：

（11）

式中 ，，和分别为系统矩阵、输入矩阵、输出矩阵和反馈矩阵，具体形式如下：

（12）

在已知结构系统的输入⁃输出数据的情况下，可采用TNSI方法辨识得到式（12）中的各个矩阵［32，36，38］，进而得到非线性结构系统的状态空间模型。进一步可计算得到非线性结构系统的扩展频响函数，如下：

（13）

式中 为非线性结构系统的标称线性系统频响函数，其形式与式（3）类似，具体为：

（14）

通过式（13）可对扩展频响函数进行分离，得到非线性参数和标称线性系统频响函数。进一步地，基于分离出的，通过采用第1.1节中提出的基于频响函数变换的局部线性连接刚度辨识方法，可辨识得到非线性结构系统的局部线性连接刚度。

1.3 局部连接刚度辨识流程

基于上述过程，可归纳出结构系统的局部连接刚度辨识流程，如图1所示。对于线性结构系统，首先基于时域的输入⁃输出数据，采用TLSI方法估计频响函数，其次对频响函数逆矩阵列元素的实部进行求和，最后用形式的二次曲线对求和结果进行拟合，取其常数项即为结构系统与边界之间的局部线性连接刚度。对于非线性结构系统，首先采用TNSI方法估计扩展频响函数，再将其进行分离可得到局部非线性连接刚度和标称线性系统频响函数，最后基于分离出的标称线性系统频响函数对局部线性连接刚度进行辨识，进而实现结构系统局部线性和非线性连接刚度的联合辨识。

2 数值验证

2.1 局部线性连接刚度辨识算例

为验证所提辨识方法的有效性，本节考虑一个三自由度结构系统数值算例，如图2所示。在第二个自由度处附加一个与边界相连的线性弹簧，其刚度为。三自由度结构系统的质量、阻尼和刚度矩阵如下所示：

（15）

在3个自由度上均施加白噪声激励，同时在得到的位移响应中加入信噪比为20 dB的噪声信号。基于激励和含噪声的位移时域数据，采用TLSI方法辨识得到三自由度结构系统的频响函数H11如图3所示，其中红色虚线为理论值，蓝色实线为辨识值。

图4给出了频响函数逆矩阵第一列到第三列的列元素实部的求和曲线，进一步用形式的二次曲线对其进行拟合，拟合结果如表1所示，其中常数项为相应自由度与边界之间的线性连接刚度，二次项系数反映的是相应自由度的质量大小。对比拟合值与理论值的偏差可知，基于频响函数变换的辨识方法具有准确获取局部线性连接刚度的能力。

将附加弹簧的刚度分别改为和，对各自频响函数逆矩阵的第二列元素的实部进行求和，得到不同连接刚度下的曲线拟合结果如表2所示，结果表明，对于不同量级的连接刚度，所提出的辨识方法均具有较高的辨识精度。

2.2 局部非线性连接刚度辨识算例

在第二个自由度处同时附加一个线性弹簧和一个单侧间隙非线性弹簧，如图5所示。单侧间隙非线性弹簧的描述函数如图6所示。

非线性恢复力的具体表达式如7式所示：

（16）

式中 d为间隙值；为间隙非线性刚度。

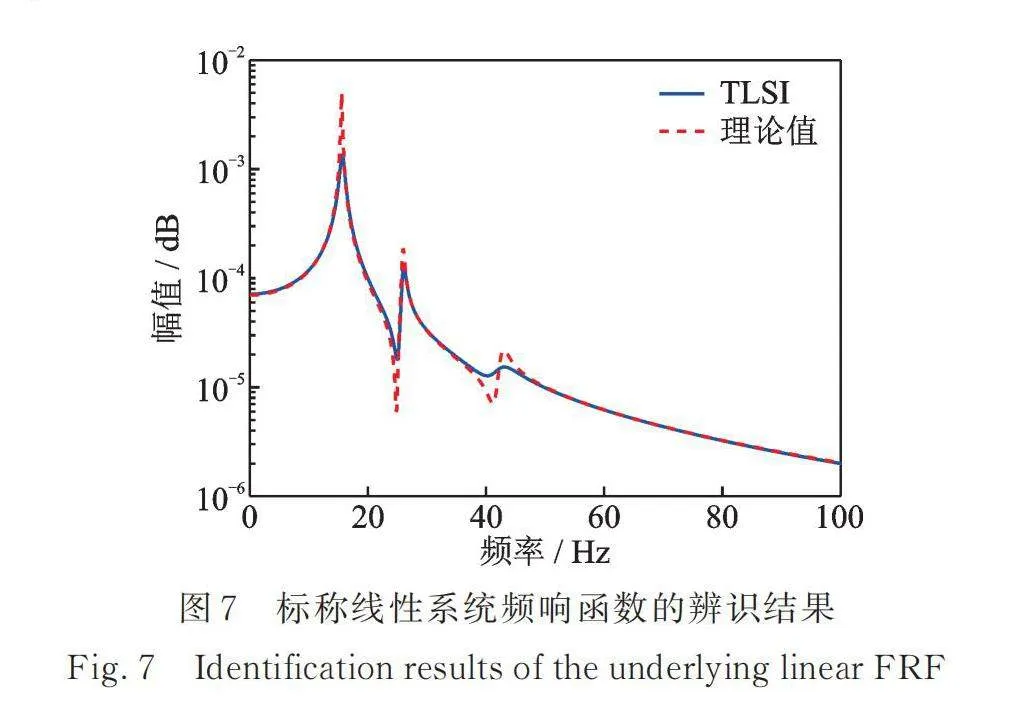
取线性弹簧刚度为，间隙非线性弹簧刚度为，间隙值为d=0.001 m。将间隙的理论值0.001 m代入非线性描述函数，采用TNSI方法对三自由度非线性结构系统进行辨识，分离出的标称线性系统频响函数如图7所示，同时可得到间隙非线性刚度的辨识结果如图8所示。

对分离出的标称线性系统频响函数矩阵求逆，图9给出了频响函数逆矩阵第二列元素实部的求和曲线及其拟合表达式，其中红色圆圈为列元素实部的求和结果，蓝色实线为其拟合后的二次曲线，可发现拟合曲线的常数项与线性连接刚度的理论值基本一致。综合图8和9的辨识结果可知，对于非线性结构系统，将基于频响函数变换的辨识方法与TNSI方法相结合，可实现结构系统局部线性和非线性连接刚度的联合辨识。

3 实验验证

对所提出的局部连接刚度辨识方法进行实验验证。对应上一节中的数值算例，搭建三自由度结构的实验系统，其原理图和实物图分别如图10和11所示。在第二层质量块m2处可附加线性和非线性弹簧，其中线性弹簧刚度可由测力计事先测量得出。为获取实验系统完整的频响函数矩阵，在每层质量块处均施加激励，同时布置加速度传感器以拾取响应信号。开展不同条件下的振动实验，然后基于输入⁃输出实测数据，采用基于频响函数变换的辨识方法和TNSI方法，对实验系统的局部附加连接刚度进行辨识。

3.1 局部线性连接刚度辨识实验

在第二层质量块处附加一个刚度为的线性弹簧，采用移动力锤法分别对3层质量块进行连续锤击激励，采样频率为2048 Hz，采样时间为8 s，其中敲击第二层质量块时的激励⁃加速度的时域数据如图12所示。

基于实验系统的输入⁃输出数据，采用TLSI方法辨识得到的频响函数曲线如图13所示，其中红色虚线为经典H1估计结果，蓝线实线为辨识结果。由图可知，二者吻合良好。

对频响函数逆矩阵第二列元素的实部求和，用形式的二次曲线对其进行拟合，如图14所示，可以发现拟合结果的常数项与真实的连接刚度基本吻合。如将附加弹簧的刚度改为，拟合结果依旧吻合良好。

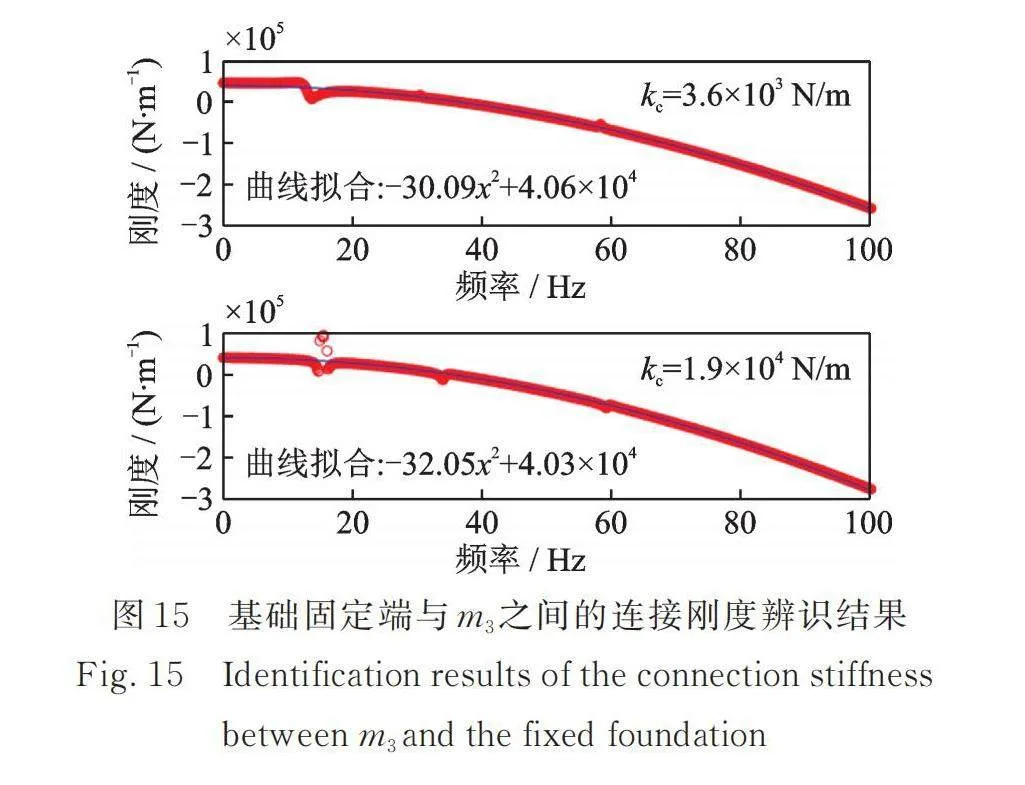
图15给出了不同附加弹簧下基础固定端与m3之间的连接刚度辨识结果，该结果由频响函数逆矩阵第三列元素的实部求和得出。对比可知，在不同附加弹簧连接刚度下，曲线拟合结果基本一致，这是由于附加弹簧并不会改变基础固定端与m3之间的连接刚度，也进一步证明了上述辨识方法及流程的合理性。综合图14和15的辨识结果可知，基于频响函数变换的辨识方法具有获取线性结构系统局部连接刚度的能力。

3.2 局部非线性连接刚度辨识实验

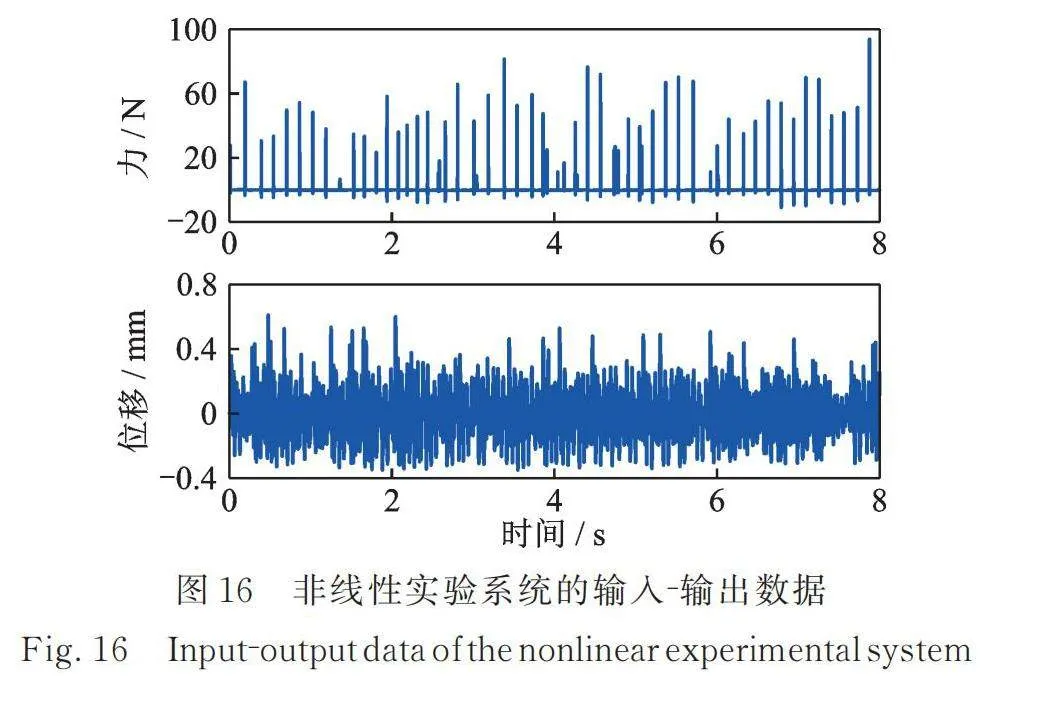
在第二层质量块处同时附加一个线性弹簧和一个单侧间隙非线性弹簧，其中线性弹簧的刚度为。在原有实验装置中加入激光位移传感器测量第二层质量块的位移，图16给出了第二层质量块处激励⁃位移的时域数据，基于位移数据可构造间隙非线性描述函数。

采用三线性函数法确定间隙值［28，32，38］，将uwP2ssMbZn9LJe6YJluvJw==假定的间隙区间［0.314 mm，0.319 mm］划分为5个等距的间隔，图17给出了区间内非线性恢复力的分布情况，可知，间隙值主要集中在0.316 mm附近。

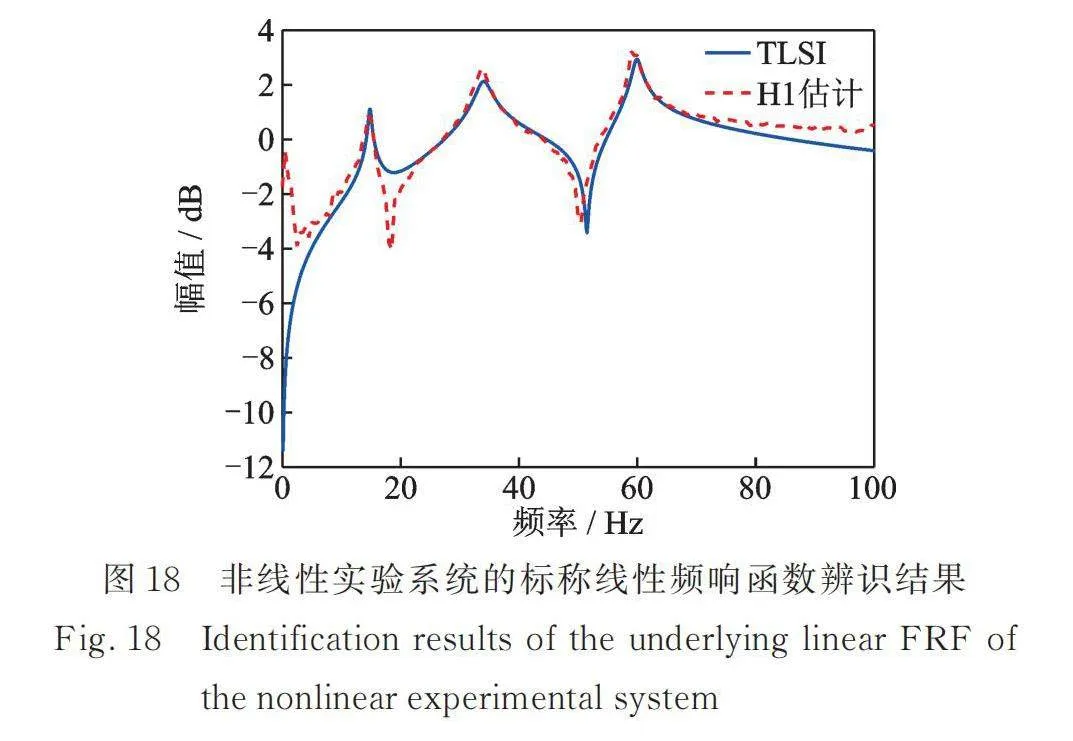
进一步将间隙值d=0.316 mm代入单侧间隙非线性描述函数中，基于非线性实验系统的输入⁃输出实测数据，采用TNSI方法对实验系统的线性部分和非线性部分进行分离。图18给出了标称线性系统频响函数H22的辨识结果，其中红色虚线为实验系统未触发间隙时的H1估计结果，蓝色实线为TNSI的辨识结果。

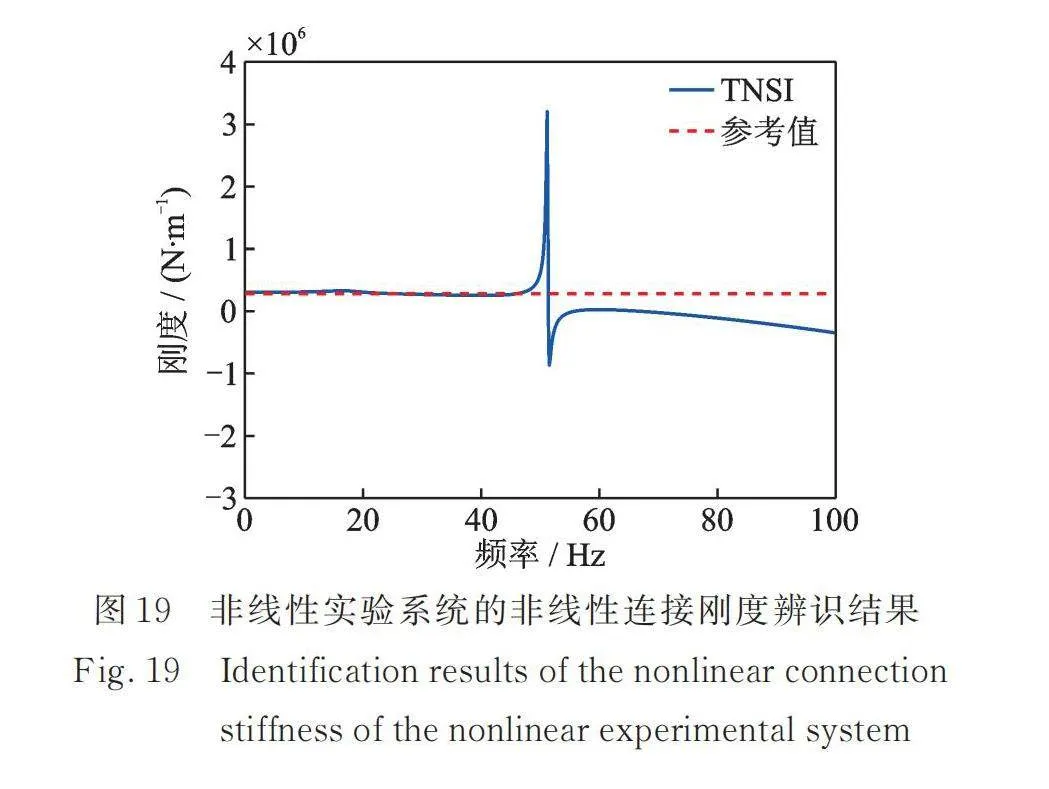
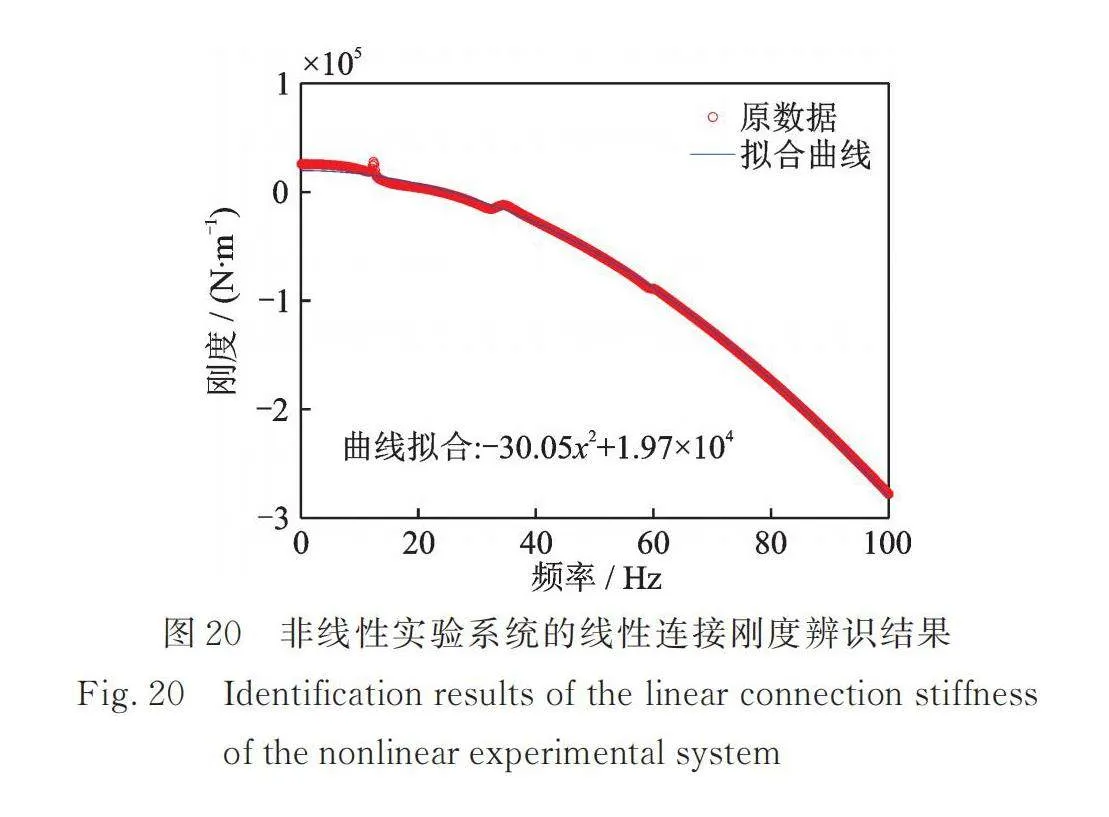
非线性弹簧连接刚度的辨识结果如图19所示。该结果在低频段较为稳定，可观察到辨识结果接近，基本符合真实的非线性连接刚度特性。基于TNSI分离出的标称线性系统频响函数，可得线性连接刚度的辨识结果如图20所示，综合图19和20的辨识结果可知，所提出的辨识方法能够对非线性结构系统中局部线性和非线性连接刚度进行联合辨识。

4 结 论

面向工程应用研究领域中的连接结构动力学问题，本文提出了一种非线性结构系统的局部连接刚度辨识方法。一方面，根据结构系统刚度矩阵的性质，提出了基于频响函数变换的局部线性连接刚度辨识方法，同时结合TNSI方法可实现局部线性和非线性连接刚度的联合辨识；另一方面，分别基于三自由度结构系统的数值算例和实验系统进行辨识方法验证。结果表明，所提方法能够对非线性结构系统中的局部线性和非线性连接刚度进行有效辨识，可用于获取非线性结构系统的局部连接刚度参数，服务工程连接结构的动力学建模与特性预示。

参考文献：

［1］王东，徐超，胡杰，等. 连接结构接触界面非线性力学建模研究［J］. 力学学报，2018，50（1）： 44-57.

Wang D，Xu C，Hu J，et al. Nonlinear mechanics modeling for joint interface of assembled structure［J］. Chinese Journal of Theoretical and Applied Mechanics，2018，50（1）： 44-57.

［2］Yuan J，El-Haddad F，Salles L，et al. Numerical assessment of reduced order modeling techniques for dynamic analysis of jointed structures with contact nonlinearities［J］. Journal of Engineering for Gas Turbines and Power，2019，141（3）： 031027.

［3］范新亮，王彤，夏遵平. 基于子结构解耦的连接特性识别新方法［J］. 力学学报，2021，53（12）： 3376-3388.

Fan X L，Wang T，Xia Z P. A new method of joint dynamic properties identification using substructure decoupling［J］. Chinese Journal of Theoretical and Applied Mechanics，2021，53（12）： 3376-3388.

［4］赵广，张泽新，袁运博，等. 榫连接结构接触刚度识别与验证［J/OL］. 航空动力学报，2023⁃11⁃08. https：//link. cnki net/urlid/11.2297.V.20231107.1613.003.

Zhao G，Zhang Z X，Yuan Y B，et al. Contact stiffness identification of tenon joint structures and verification［J/OL］. Journal of Aerospace Power. 2023⁃11⁃08. https：//link. cnki net/urlid/11.2297.V.20231107.1613.003.

［5］Li Z T，Han J L，Yun H W. Identification of piecewise linear aeroelastic systems［J］. Journal of Vibroengineering，2013，15（3）： 1526-1536.

［6］王博，马志赛，丁千，等. 基础激励下含间隙折叠舵面非线性系统辨识［J］. 振动与冲击，2020，39（4）： 122-128.

Wang B，Ma Z S，Ding Q，et al. System identification of folding rudders with freeplay nonlinearity under base excitation［J］. Journal of Vibration and Shock，2020，39（4）： 122-128.

［7］Panchal J，Benaroya H. Review of control surface freeplay［J］. Progress in Aerospace Sciences，2021，127： 100729.

［8］Festjens H，Chevallier G，Dion J L. Nonlinear model order reduction of jointed structures for dynamic analysis［J］. Journal of Sound and Vibration，2014，333（7）： 2100-2113.

［9］Zhan M，Guo Q T，Yue L，et al. Modeling and stochastic model updating of bolt-jointed structure［J］. Shock and Vibration，2018，2018： 8354249.

［10］任浩源，王毅，王亮，等. 基于非线性接触刚度的铰接/锁紧结构动力学建模方法［J］. 强度与环境，2021，48（6）： 31-38.

Ren H Y，Wang Y，Wang L，et al. A dynamic model of hinged-locking structures based on contact theory［J］. Structure and Environment Engineering，2021，48（6）： 31-38.

［11］聂肇坤，李刚，曾岩，等. 考虑舱段连接结构非线性的运载火箭动力学建模［J］. 固体火箭技术，2021，44（1）： 118-125.

Nie Z K，Li G，Zeng Y，et al. Dynamic modeling method of launch vehicle considering nonlinearity of cabin connection structures［J］. Journal of Solid Rocket Technology，2021，44（1）： 118-125.

［12］刘玉，赵迪文，艾延廷，等. 航空发动机螺栓连接结构薄层单元静力学非线性模型修正［J］. 航空动力学报，2023，38（6）： 1480-1488.

Liu Y，Zhao D W，Ai Y T，et al. Modification of static nonlinear model of thin layer element for aeroengine bolted structure［J］. Journal of Aerospace Power，2023，38（6）： 1480-1488.

［13］Zadeh L. On the identification problem［J］. IRE Transactions on Circuit Theory，1956，3（4）： 277-281.

［14］Nowak R D. Nonlinear system identification［J］. Circuits，Systems and Signal Processing，2002，21（1）： 109-122.

［15］邓杨. 基于参数化时频分析的非线性系统辨识［D］. 上海： 上海交通大学，2014.

Deng Y. Nonlinear system identification by using parameterized time-frequency analysis［D］. Shanghai： Shanghai Jiao Tong University，2014.

［16］Pang Z Y，Ma Z S，Ding Q，et al. An improved approach for frequency-domain nonlinear identification through feedback of the outputs by using separation strategy［J］. Nonlinear Dynamics，2021，105（1）： 457-474.

［17］Kerschen G，Worden K，Vakakis A F，et al. Past，present and future of nonlinear system identification in structural dynamics［J］. Mechanical Systems and Signal Processing，2006，20（3）： 505-592.

［18］Noël J P，Kerschen G. Nonlinear system identification in structural dynamics： 10 more years of progress［J］. Mechanical Systems and Signal Processing，2017，83： 2-35.

［19］Gomes G F，Mendez Y A D，Da Silva Lopes Alexandrino P，et al. A review of vibration based inverse methods for damage detection and identification in mechanical structures using optimization algorithms and ANN［J］. Archives of Computational Methods in Engineering，2019，26（4）： 883-897.

［20］Quaranta G，Lacarbonara W，Masri S F. A review on computational intelligence for identification of nonlinear dynamical systems［J］. Nonlinear Dynamics，2020，99（2）： 1709-1761.

［21］姜东，吴邵庆，史勤丰，等. 基于薄层单元的螺栓连接结构接触面不确定性参数识别［J］. 工程力学，2015，32（4）： 220-227.

Jiang D，Wu S Q，Shi Q F，et al. Contact interface parameter identification of bolted joint structure with uncertainly using thin layer element method［J］. Engineering Mechanics，2015，32（4）： 220-227.

［22］蒋国庆，洪荣，陈万华. 螺栓法兰连接结构简化动力学建模及模型参数辨识［J］. 振动与冲击，2020，39（15）： 170-175.

Jiang G Q，Hong R，Chen W H. Simplified dynamic modeling and model parametric identification for bolted flange connection structures［J］. Journal of Vibration and Shock，2020，39（15）： 170-175.

［23］南宫自军，陈磊磊，王杰. 典型航天结构连接刚度辨识及建模方法研究［J］. 导弹与航天运载技术（中英文），2022（6）： 21-25.

Nangong Z J，Chen L L，Wang J. Research on the modeling and identification of connection stiffness for typical aerospace structure［J］. Missiles and Space Vehicles，2022（6）： 21-25.

［24］Noël J P，Kerschen G，Foltête E，et al. Grey-box identification of a non-linear solar array structure using cubic splines［J］. International Journal of Non-Linear Mechanics，2014，67： 106-119.

［25］Noël J P，Marchesiello S，Kerschen G. Subspace-based identification of a nonlinear spacecraft in the time and frequency domains［J］. Mechanical Systems and Signal Processing，2014，43（1-2）： 217-236.

［26］De Filippis G，Noël J P，Kerschen G，et al. Model reduction and frequency residuals for a robust estimation of nonlinearities in subspace identification［J］. Mechanical Systems and Signal Processing，2017，93： 312-331.

［27］Ma Z S，Wang B，Zhang X，et al. Nonlinear system identification of folding fins with freeplay using direct parameter estimation［J］. International Journal of Aerospace Engineering，2019，2019： 3978260.

［28］Sun Y K，Yang C，Wu Z G，et al. Nonlinear system identification of an all movable fin with rotational freeplay by subspace-based method［J］. Applied Sciences，2020，10（4）： 1205-1222.

［29］孙玉凯，杨超，吴志刚. 含间隙非线性二元翼段的系统辨识［J］. 北京航空航天大学学报，2021，47（1）： 140-149.

Sun Y K，Yang C，Wu Z G. System identification of a 2-DOF wing section with freeplay nonlinearity［J］. Journal of Beijing University of Aeronautics and Astronautics，2021，47（1）： 140-149.

［30］Adams D，Allemang R J. A new derivation of the frequency response function matrix for vibrating non-linear systems［J］. Journal of Sound and Vibration，1999，227（5）： 1083-1108.

［31］Adams D E，Allemang R J. A frequency domain method for estimating the parameters of a non-linear structural dynamic model through feedback［J］. Mechanical Systems and Signal Processing，2000，14（4）： 637-656.

［32］Marchesiello S，Garibaldi L. A time domain approach for identifying nonlinear vibrating structures by subspace methods［J］. Mechanical Systems and Signal Processing，2008，22（1）： 81-101.

［33］Marchesiello S，Fasana A，Garibaldi L. Modal contributions and effects of spurious poles in nonlinear subspace identification［J］. Mechanical Systems and Signal Processing，2016，74： 111-132.

［34］Zhang M W，Wei S，Peng Z K，et al. A two-stage time domain subspace method for identification of nonlinear vibrating structures［J］. International Journal of Mechanical Sciences，2017，120： 81-90.

［35］Liu J，Li B，Miao H H，et al. A modified time domain subspace method for nonlinear identification based on nonlinear separation strategy［J］. Nonlinear Dynamics，2018，94（4）： 2491-2509.

［36］Ma Z S，Pang Z Y，Liang J X，et al. A novel output-only time-domain nonlinear subspace approach for identifying vibrating structures with clearance nonlinearity［J］. Journal of Sound and Vibration，2021，511： 116332.

［37］Zhu R，Jiang D，Marchesiello S，et al. Automatic nonlinear subspace identification using clustering judgment based on similarity filtering［J］. AIAA Journal，2023，61（6）： 2666-2674.

［38］庞志雅. 基于输出反馈思想的间隙非线性系统辨识方法研究［D］. 天津： 天津大学，2021.

Pang Z Y. Research on identification methods of nonlinear systems with clearance based on output feedback［D］. Tianjin： Tianjin University，2021.

Local connection stiffness identification for nonlinear structural systems

REN Yan-song1，2，MA Zhi-sai1，2，LI Ya-nan3，YU Jia-hui3，ZHANG Zhong3，DING Qian1，2

（1.School of Mechanical Engineering，Tianjin University，Tianjin 300350，China； 2.Tianjin Key Laboratory of Nonlinear Dynamics and Control，Tianjin 300350，China； 3.Beijing Institute of Structure and Environment Engineering，Beijing 100076，China）

Abstract： Jointed structures are widely used in engineering applications，and local nonlinear characteristics at the connection interface have an important influence on their dynamic modeling and characteristic prediction. Aiming at the problem that local connection parameters of nonlinear structural systems are unknown or difficult to measure，this paper proposes an identification method of local linear connection stiffness based on the FRF transformation from the perspective of inverse dynamic problems. By further combining with the time-domain nonlinear subspace identification method，the local linear and nonlinear connection stiffness of nonlinear structural systems can be finally obtained. The numerical example and experimental setup of the three degrees-of-freedom structural system are designed and further built to validate the proposed method. The results demonstrate that the proposed method can separate and identify the underlying linear FRF and nonlinear parameters of the nonlinear structural system，and subsequently realize the joint identification of the local linear and nonlinear connection stiffness.

Key words： connection stiffness identification；jointed structure；nonlinear system；nonlinear subspace identification method

作者简介： 任彦松（1999―），男，硕士研究生。E-mail： renystju@163.com。

通讯作者： 马志赛（1988―），男，博士，副教授。E-mail： zhisai.ma@tju.edu.cn。