附加式声学黑洞对悬臂板振动寿命影响研究

摘要： 结构在振动条件下的疲劳破坏对其自身的使用寿命以及使用者的人身安全均带来了隐患，目前对于解决结构振动疲劳有添加加强筋、敷设大量阻尼材料等方法，但往往效率较低，附加质量过大。为解决上述问题，提出将附加式声学黑洞（ABH）安装在结构上，通过降低结构响应达到降低应力幅值，延长使用寿命的目的。以悬臂板为基准结构，利用有限元方法进行了稳态动力学分析。结果表明，在附加矩形声学黑洞（RABH）后，悬臂板缺口处的应力响应明显降低。通过应力实验以及疲劳实验，验证了附加RABH可以降低结构危险点处应力响应，并延长悬臂板结构的振动疲劳寿命。

关键词： 声学黑洞； 悬臂板； 振动疲劳

中图分类号： TB535； O346.2 文献标志码： A 文章编号： 1004-4523（2024）10-1669-10

DOI：10.16385/j.cnki.issn.1004-4523.2024.10.004

引 言

随着工业水平的飞速发展，对于大型机械与装备的要求不仅仅局限于更高更快的性能，更体现在可靠性、使用寿命等问题上。而这些装备在使用中都要面临严重的振动问题，当其持续在振动环境下工作时，会面临结构振动疲劳失效的威胁，不仅大大缩减了装备的使用寿命，而且由于疲劳失效往往是长时间积累后的突然爆发，也会对装备使用者的人身安全造成难以估量的后果［1］。在中国飞机研制历程中，也遇到过由于结构共振导致疲劳失效的问题。例如某型飞机液压管的固有频率为535～537 Hz，而与其配套的液压泵的工作频率为528～540 Hz，在工作时发生共振现象，导致液压导管出现裂纹，飞机烧毁［2⁃3］。

20世纪70年代开始，基于发展振动强度试验的需求，国内研究人员提出了振动疲劳这一全新概念。王明珠［4］和姚卫星［5］认为，当振动频率与结构固有频率相当时，可视作振动疲劳问题；当振动频率低于结构固有频率时，可视作普通静态疲劳问题；当振动频率超出结构固有频率很多，已经接近声波的频率时，可视作声疲劳问题。姚起杭等［6］认为，振动疲劳是结构所受动态交变载荷（如振动、冲击、噪声载荷等）的频率分布与结构固有频率分布具有交集或相接近，从而使结构产生共振所导致的疲劳破坏现象。各位学者对于振动疲劳的定义虽然不尽相同，但对于振动疲劳的破坏机理，普遍还是认为与静态疲劳是一致的，均为交变应力所导致。当结构在振动环境下工作，交变载荷的频率接近结构固有频率时，结构动响应会迅速增大，交变应力也会随之增大，从而加快裂纹的产生［7］。

因此，结构振动疲劳寿命的预测与一般静态疲劳的寿命分析思路一致。首先结合外部载荷与模型得到结构响应，确定结构危险点位置，根据材料的疲劳性能曲线以及结构累计损伤理论，例如Miner线性累计损伤理论，进行疲劳寿命预测。在随机振动环境下，载荷较为复杂，结构的应力⁃应变响应需要进行一定的处理和等效。

目前振动疲劳寿命的估算方法主要分为频域法与时域法，时域法由于需要进行时域模拟，计算量极大，因此相关研究较少。频域法是在频域内利用响应功率谱密度（PSD）的谱参数描述响应应力信息，将较为复杂的应力响应转化为可以用于振动疲劳寿命估算的数据。目前主要使用的统计方法为峰值分布法与幅值分布法。峰值分布法主要应用于高斯分布过程，其峰值与谷值容易得到，但结构疲劳损伤主要由幅值决定，可以利用峰值概率密度函数得到等效应力或通过峰值循环计数处理得到幅值信息，进而进行寿命估算。而幅值分布法则可以通过雨流幅值分布模型直接进行疲劳寿命估算［4］。

目前对于振动疲劳的处理方法通常为在共振处安装加强筋、添加阻尼或者引入其他振动控制技术，但上述措施仍存在附加质量过大、控制系统复杂、效率不高等问题，大大降低了结构的可靠性。对振动疲劳的抑制亟需更高效、更便捷的解决方法。

声学黑洞（Acoustic Black Hole，ABH）结构是一种新型的波控制结构，得益于其重量轻、频率宽、效率高的特点而广受学者们的关注［8‑10］。当ABH结构的厚度h和到边缘的距离x满足幂函数，弯曲波的波速在变厚度结构传播过程中会逐渐减小，理论上当结构厚度减小到零时，弯曲波波速也随之为零，产生零反射现象［11］。传统的ABH在使用时，常内嵌入主结构作为陷波器使用［12］，Deng等［13］将声学黑洞嵌入圆柱体内，为ABH在舱体等场景下使用提供了可能。这样虽然可以产生良好的振动控制效果，但不可避免地会对主结构产生破坏，从而影响主结构整体的刚度与强度。针对这个问题，文献［14⁃17］结合动力吸振器的原理提出了附加式ABH用于结构的减振，并设计出一系列附加式ABH结构，例如圆盘形ABH结构、偏心圆盘形AABH结构。Deng等［18］探究了附加式ABH在梁结构上的最佳排布方法，展现了其在隔振方面的优异前景。Sheng等［19］将附加式ABH与失调效应相结合，显著地拓宽了作用频带，提升了衰减效果。Zhou等［20］提出了一种平面涡流型声学黑洞，以最小的空间获得了极长的黑洞区域。Deng等［21］提出一种声学黑洞复合板结构，将周期性ABH附加在主板上，为板的吸振提供了一种可靠、有效的手段。对于ABH自身的振动疲劳问题，Du等［22］基于高斯展开法对声学黑洞梁结构及板结构进行了随机振动疲劳分析，并确定了两种结构的危险点，为ABH结构随机振动疲劳分析提供了参考。而附加式ABH作为对结构共振状态下动响应有极强削减能力的器件，在控制振动疲劳危害这一方面应用还没有相关研究。

因此，本文针对悬臂板结构第一阶弯曲共振模态，结合声学黑洞效应以及动力吸振原理，设计出矩形声学黑洞（Rectangle Acoustic Black Hole，RABH）动力吸振器。在不改变悬臂板结构强度与刚度的前提下，通过附加的形式添加RABH，降低主结构在共振下的动响应，进而减小共振频率下危险点的应力水平，最终达到抵抗振动疲劳，延长结构寿命的目的。

1 RABH结构设计及性能验证

1.1 RABH结构设计

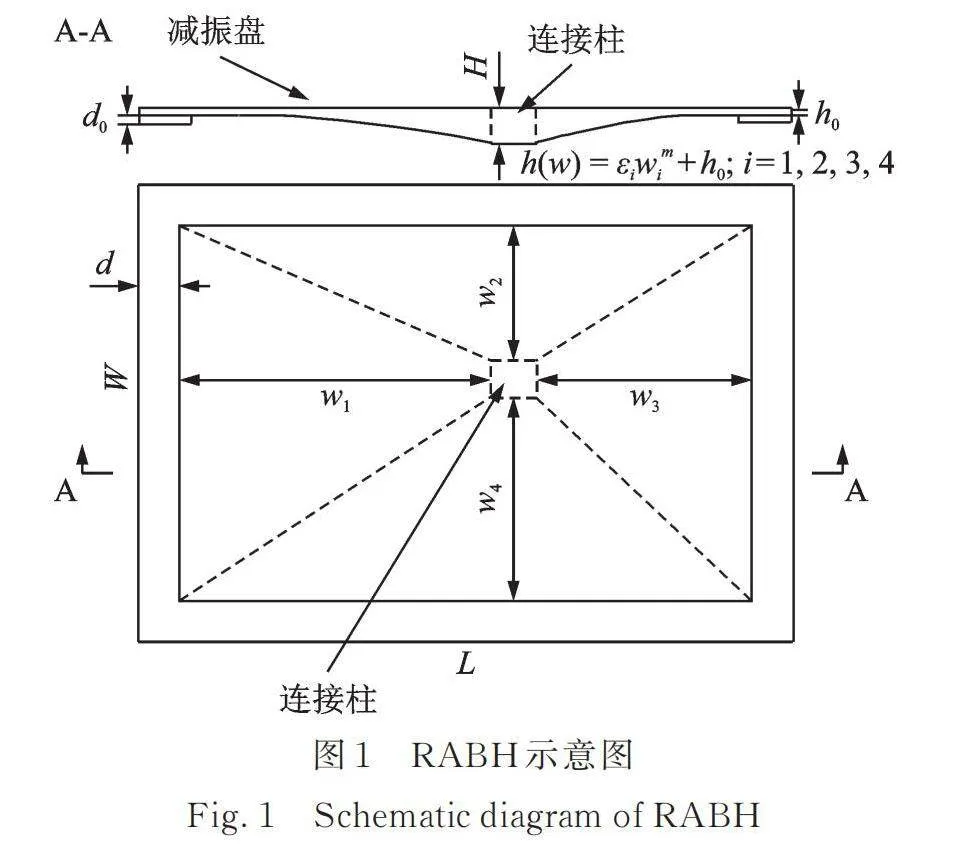
RABH由连接柱、裹设在连接柱外周面的减振盘与减振盘四周包围的均匀层组成。如图1所示，RABH由中心连接柱的四个外周面按照减振盘纵截面的厚度变化规律向远离连接柱的方向延伸，延伸长度分别为w1，w2，w3和w4，构成矩形减振盘区域，在减振盘区域四周包围一圈宽度为d、厚度为h0的均匀层，在日常使用中，一般会在RABH四周边缘区域安装一圈厚度为d0的丁基橡胶减振环。减振盘纵截面的厚度变化规律为：

（1）

式中 h（w）为减振盘纵截面的厚度；εi为i方向上厚度变化系数；wi为i方向上减振盘一点所对应横截面到减振盘边缘的距离；m为函数幂次，需要满足才能有效发挥声学黑洞效应；h0为减振盘区域最小厚度，同时也是均匀层区域的厚度。

1.2 有限元建模

为研究ABH对延长结构振动疲劳寿命的作用效果，首先在ABAQUS有限元仿真软件中进行动力学分析。本文选取如图2所示的悬臂板结构作为研究对象，悬臂板几何参数如图2所示，材料采用铝，材料属性如表1所示。

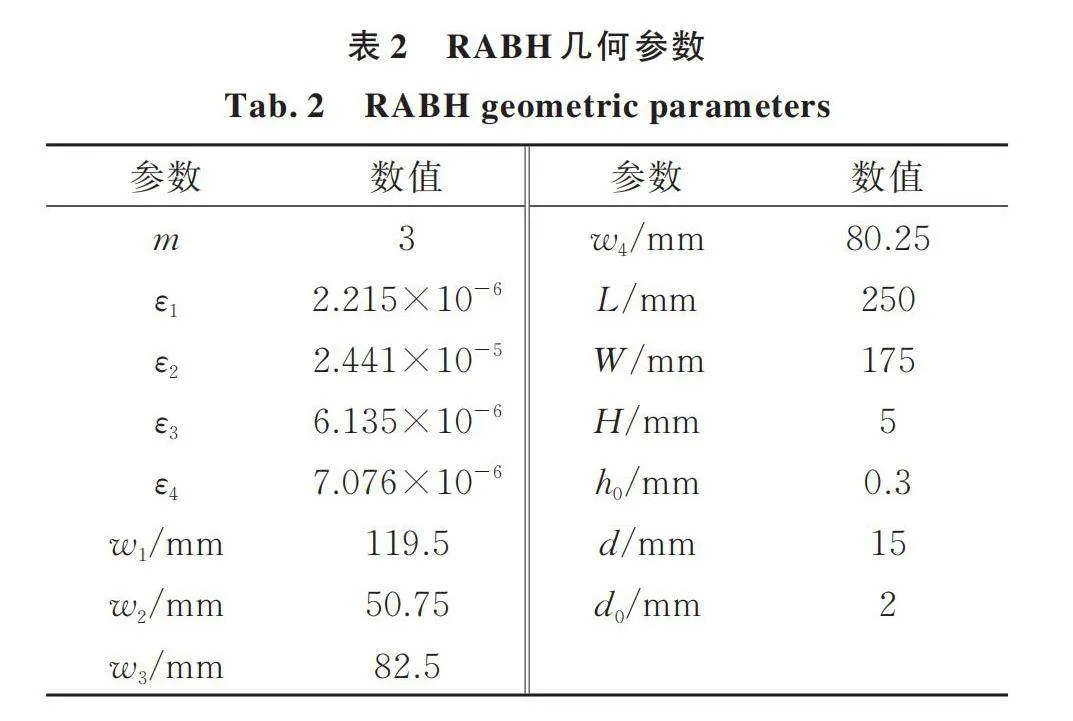
为了说明添加RABH对悬臂板振动疲劳寿命的影响，在悬臂板自由端分别添加RABH、等质量结构（Equal Mass，EM）与等质量块做对比研究，其质量均为160 g，其中，EM为质量与RABH完全相同的均匀厚度结构，并且在相同位置布置等质量的阻尼材料；等质量块为质量与RABH完全相同的长方体结构，不布置阻尼材料。RABH材料为铝，阻尼材料为丁基橡胶，材料参数如表1所示，几何参数如表2所示。图3为RABH⁃悬臂板的合成系统图，以悬臂板左端中点为原点，在（341 mm，0 mm）处添加RABH，EM和等质量块。

悬臂板结构与三种附加结构均采用二次网格三维实体单元（C3D20R），采用非均匀网格划分方法，厚度方向均保证至少2个单元，在RABH变厚度区域确保每个波长至少有10个单元。附加结构与悬臂板采用Tie连接的方式装配，在悬臂板的矩形夹持区域内施加固支约束。通过稳态动力学的模态法，对固支夹持区域施加z方向1 m/s2加速度的载荷，计算0～100 Hz的应力频响函数。这里对于附加结构的安装位置没有做优化，根据已有的附加式声学黑洞安装位置研究，一般将附加式声学黑洞安装在振动幅值最大处，可以最大程度发挥作用，因此将附加结构安装在悬臂板振动最大的自由端端部。

1.3 悬臂板上应力动力学仿真

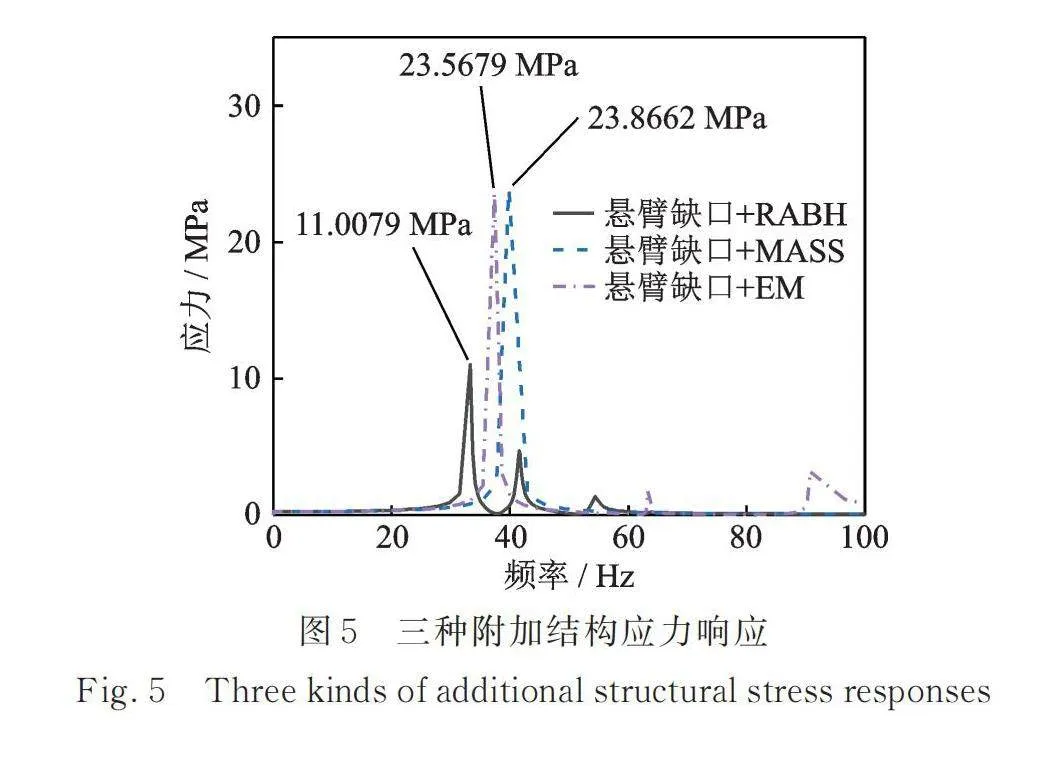
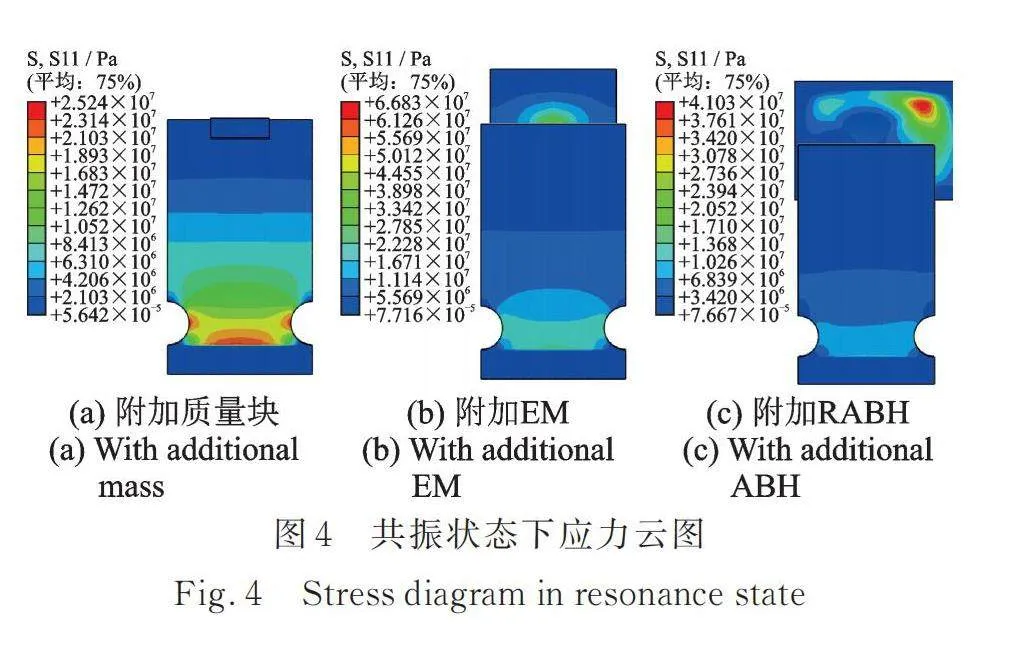
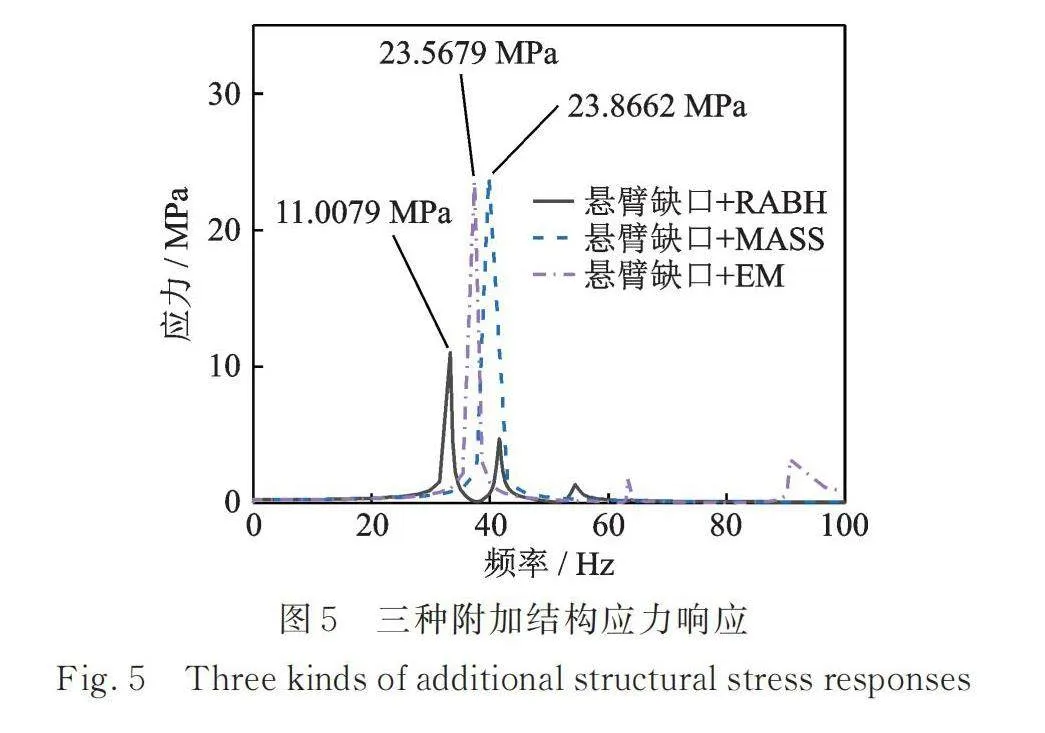
对悬臂板系统在0～100 Hz进行扫频，计算其在z方向基础激励1 m/s2加速度载荷下部件的应力分布情况，提取三种附加结构与悬臂板耦合系统共振频率下的应力云图如图4所示。可以观察到，悬臂板上凹口处的应力水平最大。提取悬臂板凹口处应力数值如图5所示。

附加等质量块时，前100 Hz的应力峰值出现在39.75 Hz处，凹口处应力大小为23.9 MPa；在附加EM的情况下，应力峰值出现在37.32 Hz处，凹口处的应力大小为23.6 MPa；在附加RABH的情况下，应力峰值出现在33.24 Hz处，凹口处应力大小为11 MPa。以上数据表明，添加RABH后悬臂板上应力峰值相比添加质量块后的应力峰值降低了约2倍。而附加EM后悬臂板凹口处应力却几乎没有减小，这主要是由于EM没有与主结构产生耦合，导致其附加的阻尼不能很好地发挥效果。为了更直观地体现附加RABH对悬臂板共振状态下应力峰值的削弱效果，将三种情况的悬臂板应力云图参考边界统一，如图6所示，可以更加直观地看到附加RABH后，悬臂板上的应力水平有着明显的降低。

以上数据是基于悬臂板结构应力峰值的比较，值得注意的是，对于附加RABH与EM的悬臂板系统，虽然悬臂板上出现应力峰值的位置没有改变，但整个系统的最大应力值却出现在附加结构本身上，RABH结构在33.24 Hz时达到了最大应力41 MPa，而EM的最大应力已经达到66.8 MPa，均超过了附加质量块时悬臂板系统的最大应力。这意味着RABH与EM这两种附加结构的工作寿命可能会小于附加质量块情况下悬臂板的寿命。对于EM来说，其对悬臂板应力的减小极其有限，自身最大应力却是附加质量块悬臂板最大应力的2.8倍；对于RABH来说，其对悬臂板应力的减小有一定的贡献，可以将悬臂板凹口处的应力减小一半，但是RABH自身最大应力也是附加质量块悬臂板最大应力的1.7倍，对于目前的RABH来讲其工作寿命可能还无法覆盖附加RABH后悬臂板的振动疲劳寿命，但其减小应力的效果还是有所体现。

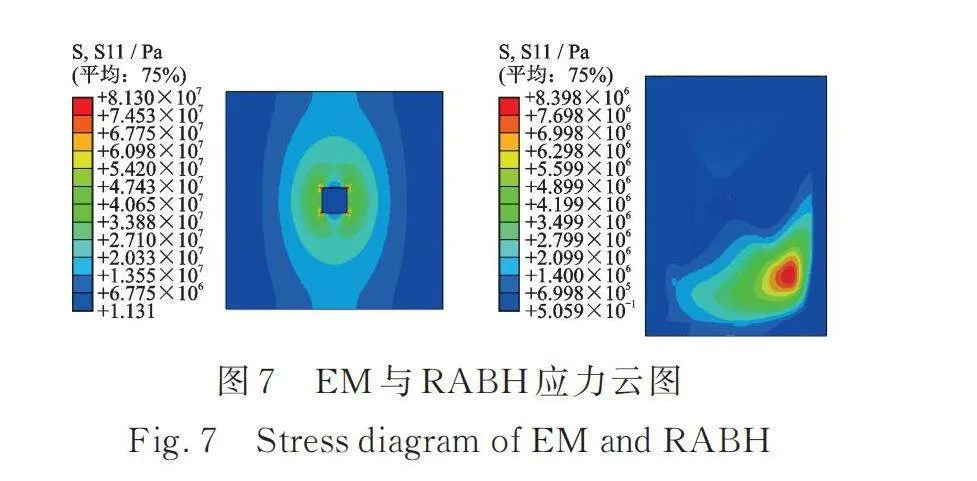
附加在悬臂板上的RABH与EM应力水平受悬臂板响应的影响，可能无法真实地反映出其自身的应力响应水平。为了消除悬臂板响应的影响，将RABH与EM的连接柱固支，并施加一个z方向1 m/s2的基础激励，提取两种结构前100 Hz响应最大的应力云图，如图7所示。可以观察到，RABH的最大应力依然出现在最长的斜边上，为8.398 MPa，EM的最大应力出现在连接柱的角上，为81 MPa，前100 Hz内RABH结构的最大应力在同样的载荷条件下比EM结构的最大应力小10倍左右，将云图调整至同一参考边界，如图8所示，可以更清晰地看到整个EM板面的应力几乎都大于RABH的最大应力。这说明了RABH的变厚度设计在自身应力响应控制方面要优于EM的阶梯式连接，但如何进一步减小自身应力水平，延长RABH工作寿命还需要进一步研究。

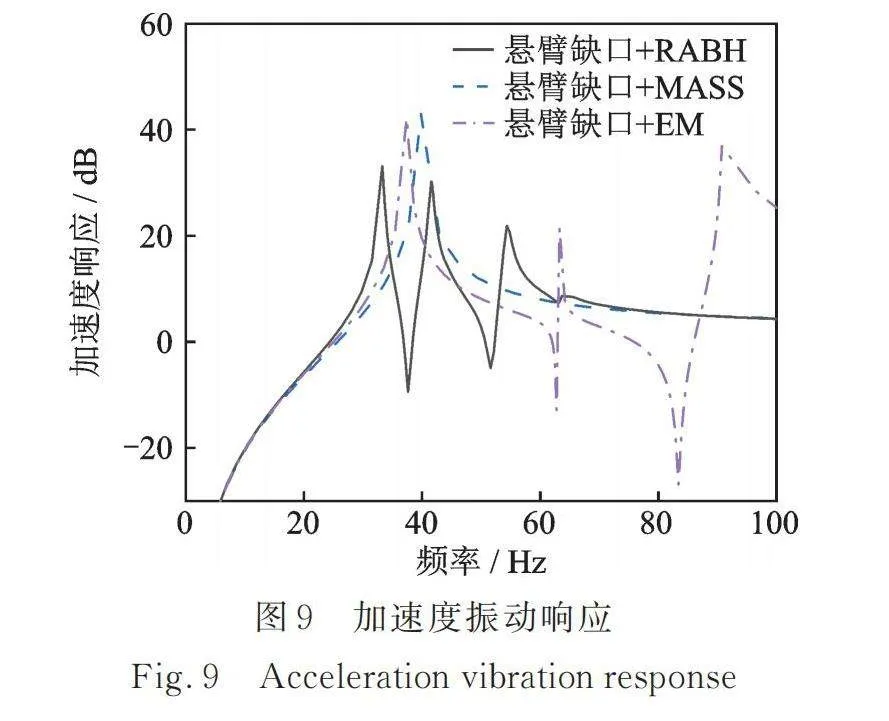
有研究表明，结构共振时的应力水平与共振时的动响应以及结构损失因子有密切联系。而附加式RABH可以高效地降低主结构动响应并且提高系统损失因子，为了进一步说明RABH减小悬臂板共振状态下应力响应的作用机理，提取了悬臂板自由端端部的振动加速度响应如图9所示。

根据加速度响应图可以看出，附加等质量块的振动响应依旧只在39.75 Hz处有一个共振峰，附加EM的最大峰值出现在37.24 Hz ，同时可以看到附加RABH的系统发生了共振峰分裂的动力吸振现象，也就是说对于悬臂板第一阶模态的振动，RABH既可以发挥动力吸振作用又可以发挥ABH高效的阻尼耗散作用，从而大幅减小振动响应，而附加EM的系统只发挥了其粘贴少量阻尼的作用，导致阻尼作用很有限。观察峰值可以发现，附加RABH后最大峰值为33.1 dB，相较于质量块降低了10 dB，而附加EM只降低了0.7 dB。以上数据一定程度上验证了结构共振时应力大小与动响应大小的联系，证明了RABH具备高效降低结构共振时动响应的能力，并且以此减小结构共振状态下的应力水平，延长振动疲劳寿命。

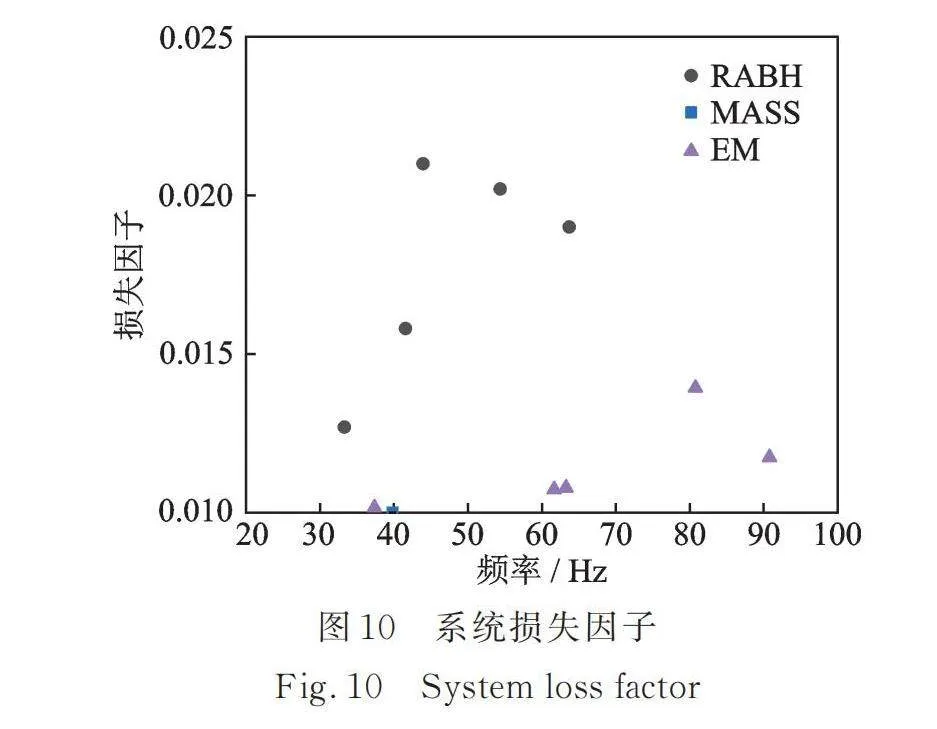
对于结构动响应的衰减，很大一部分是归功于RABH高效能量耗散作用。通过附加RABH可以极大地提高系统的损失因子，提高减振效果。提取系统损失因子，如图10所示。对于附加质量块的系统，由于质量块与悬臂板的材料都为铝，因此系统损失因子和铝一致，为0.01。附加EM系统损失因子均在0.01015～0.0139之间，而附加RABH的系统损失因子在0.0127～0.021之间，对比EM系统有着一定的提升；而在系统共振频率附近附加RABH的损失因子为0.0127，附加EM的损失因子为0.01015，其主要原因是EM无法与悬臂板第一阶模态耦合，EM上的阻尼材料无法发挥作用，而RABH在此频率与悬臂板产生耦合，发挥了其能量聚集效应，使振动能量聚集在布满阻尼材料的结构边缘，高效发挥阻尼的耗散作用，这也解释了为何附加EM的加速度响应要大于附加RABH的系统。

综上所述，附加RABH的系统中RABH可以与主结构产生动力吸振效应，并且能充分发挥ABH能量聚集效应以提高系统损失因子。以此减小整个系统的动响应，并减小悬臂板上应力水平，为RABH对悬臂板振动疲劳寿命的延长提供理论支持。

1.4 悬臂板其他应力降低措施分析

由上文的分析得到，通过在悬臂板端部附加RABH的方法能够有效降低悬臂板缺口处的应力水平，在本节中将计算在悬臂板上添加加强筋的方法对结构应力的降低效果，以探究附加RABH相较于传统方法的优势。此外，在上文的研究中，附加RABH质量约占悬臂板质量的20%，且附加质量在悬臂板的自由端，而应力最大处接近根部，附加的质量是否会影响悬臂板的应力响应也需要进一步分析。因此本节还将计算无附加质量悬臂板的应力响应，以分析附加质量的影响。

在悬臂板正反两面共添加14条加强筋，加强筋长度为310 mm，覆盖悬臂板自由区域，每条加强筋重12.6 g，总附加质量为176.4 g，略大于RABH的重量。计算带加强筋悬臂板系统与无附加的悬臂板在0～100 Hz扫频，z方向基础激励1 m/s2加速度载荷下部件的应力分布情况，提取两种悬臂板系统共振频率下的应力云图如图11所示。

由图11（a）可见，无附加的悬臂板最大应力为19.9 MPa，出现在47.88 Hz时，与上文附加质量块的23.9 MPa和RABH的11 MPa等结果对比可以得出，在悬臂板自由端附加质量会引起根部应力响应水平的增大，但附加RABH所带来的阻尼效应和动力吸振效应可以弥补附加质量引起的应力响应增大，并进一步削弱悬臂板应力响应。

由图11（b）可见，添加了加强筋的悬臂板最大应力减小为13.67 MPa，出现在67.56 Hz时，而重量更轻的RABH方案最大应力仅为11 MPa，因此RABH不管是在重量上还是效果上比传统的加强筋方案都有明显的优势，验证了附加式声学黑洞在延长结构振动寿命方向有着非常好的前景。

2 试验验证

2.1 RABH降低主结构动响应及应力特性验证

本节内容利用振动台系统，对悬臂板分别附加质量块和RABH时的加速度响应以及应变大小进行研究，以验证RABH对于悬臂板共振时应力的影响，为接下来的疲劳试验提供一些数据支撑。试验测试系统如图12所示，包括激励部分与测试部分。激励部分由苏试公司的振动控制系统产生激振信号，通过功率放大器，驱动振动台产生振动；测试部分通过东华公司的采集卡，采集加速度计以及应变片的数据，将数据传回计算机内的东华采集软件进行分析处理。

本次试验使用的悬臂板以及RABH尺寸与仿真计算中的相同，材料均为铝，悬臂板重量为1052 g，由于加工误差和阻尼裁切粘贴误差，RABH的实际重量为203 g，质量块的重量为200 g，占悬臂板重量的20%左右。RABH与质量块通过螺栓与螺母安装在悬臂板上，悬臂板通过夹具与振动台连接在一起。

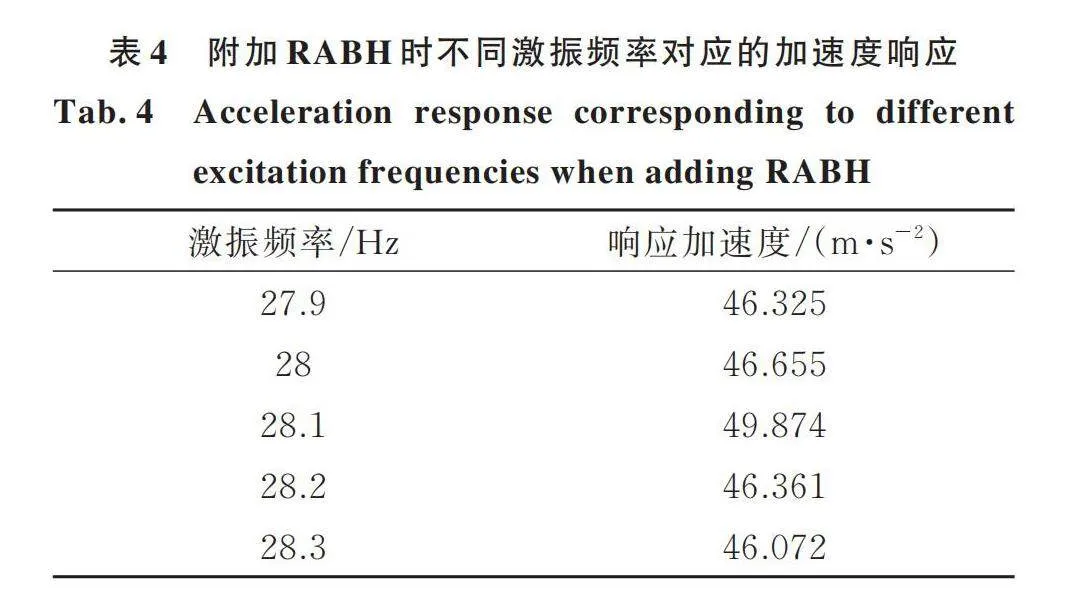
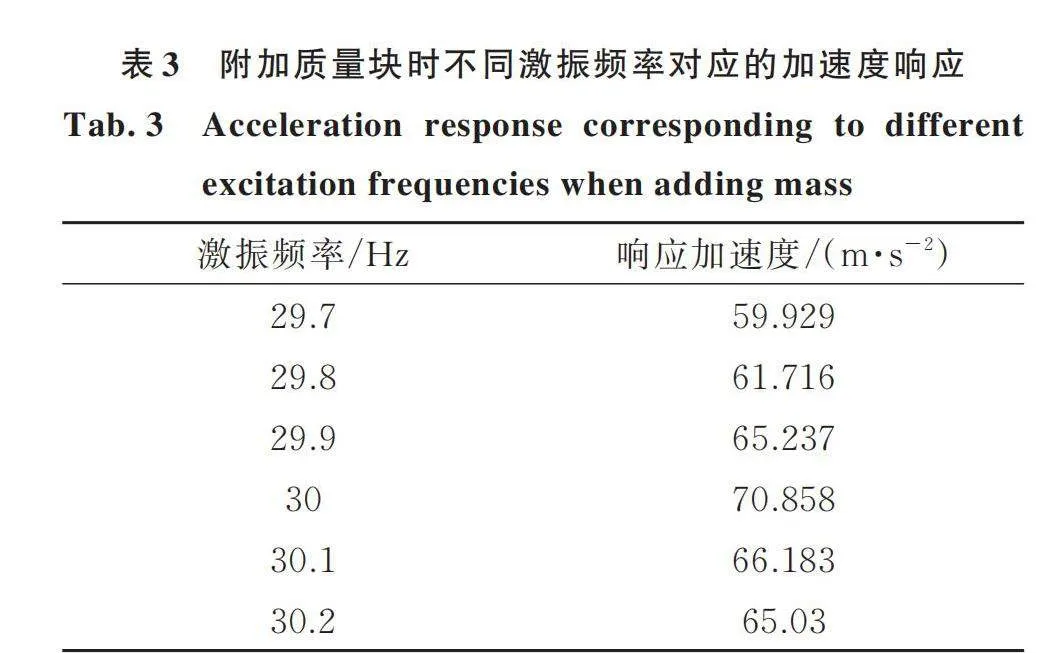
由于试验的目的是比较悬臂板在共振状态下附加RABH与质量块的应力与加速度响应的区别。为了找到结构共振频率，在共振频率附近以0.1 Hz为间隔步，步进式进行单频激励，同时测试加速度响应，最终找到响应最大的频率作为系统的共振频率。本次试验激振加速度为0.1g，为了确保试验数据可信，本次试验在同一根悬臂板上完成，两种附加情况下的加速度计以及应变片粘贴位置均一致。试验布置如图13所示，附加质量块以及附加RABH的加速度数据表3和4所示。

由表3，4数据可以确定结构的共振频率，附加质量块时为30 Hz，附加RABH时为28.1 Hz。将这两种附加结构以此频率定频激励，加速度设定为0.1g，测试得到两种附加结构凹口处应变如图14所示。

由图14可以得到，附加RABH的凹口处有着100 με左右的下降，并且加速度响应水平也有着明显的降低，这说明附加RABH可以有效地降低主结构的动响应水平以及应力水平。计算附加质量块的悬臂板凹口处应力为21 MPa左右，附加RABH的应力为14 MPa左右，为接下来的疲劳试验提供了一定的数据支撑。与仿真结果对比，附加质量块时应力值为23.9 MPa，附加RABH时为11 MPa，附加质量块结果对应较好，附加RABH时效果没有达到仿真中的效果，分析其原因主要有两点，一是边界条件的影响，试验中的夹具达不到仿真中的完全固支；二是由于加工误差导致RABH模型不够精确，与悬臂板的耦合程度未达到仿真计算中的水平，影响了能量聚集效果。

2.2 悬臂板结构振动疲劳寿命验证

本次试验的主要目的是测试附加质量块以及附加RABH的悬臂板系统的振动疲劳寿命，并验证RABH在延长结构振动疲劳寿命方面的实际效果。

构建如图15所示的振动疲劳试验系统。本次试验使用的是振动台系统中的水平滑台，通过夹具将悬臂板固定在振动台的水平滑台上。由于在振动的过程中，悬臂板的固有频率会有变化，为了确保结构始终处于共振的频段内，本次试验的激励形式为1 Hz的窄带扫频激励，中心频率为悬臂板初始的共振频率。经过初步的扫频测试，以附加质量块与附加RABH的悬臂板扫频条件下加速度响应最大的频率作为初始共振频率，分别为29.1和28.2 Hz，因此最终两种附加形式的悬臂板疲劳试验的振动频率分别为28.6～29.6 Hz与27.7～28.7 Hz，设定振动台激励形式为扫频。由于载荷频率在结构固有频率附近，响应较大，为确保结构应力响应水平处于疲劳区且不处于塑性破坏区，经过预实验确定激励加速度为0.6g。每隔30 min停止振动检查悬臂板的状态，并确保夹具保持紧固状态。

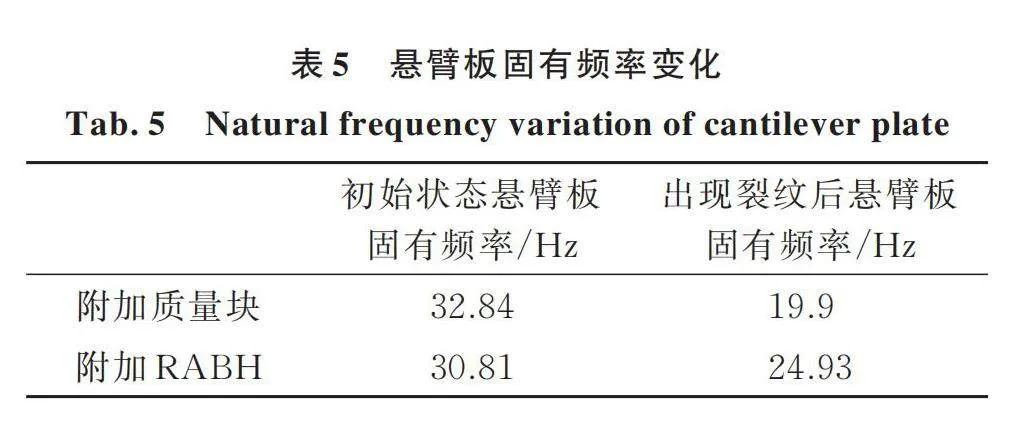
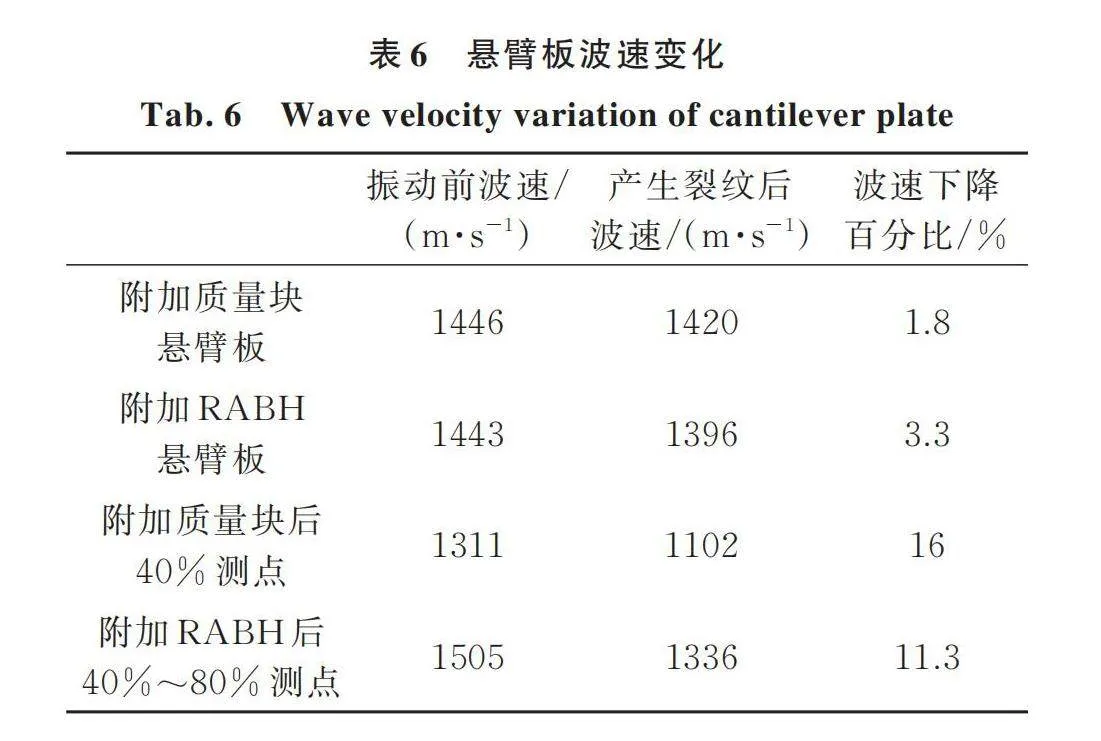
关于振动疲劳试验的终止条件目前还没有一个明确的标准，大部分是采用固有频率的下降作为判断标准，但是对于本次试验的样件固有频率只有30 Hz左右来说，5%左右固有频率的下降所对应的只有1.5 Hz左右，在实际测试中发现，夹具的松紧程度、振动台冷却系统的噪声，包括力锤测试本身的实验误差都会影响到结构固有频率的准确性，难以分辨测得的固有频率的下降是外界条件的干扰还是试件本身的固有频率下降。为了确保结构寿命测试的准确性，本次试验的终止条件为悬臂板结构出现肉眼可见的裂纹，并且将固有频率的下降作为判断试件是否疲劳失效的辅助评判标准。同时为了使试验数据更加可信，本次试验还引入了悬臂板波速的测量，振动疲劳会使结构刚度下降，波速也会有明显的下降，因此这里同时用结构波速的下降作为悬臂板疲劳失效的辅助评价标准。固有频率的测试使用的是力锤法，波速的测量是由压电片给出波信号，利用激光测振仪对悬臂板上取得的测试点进行测量，其中测试区域位于悬臂板凹口区域，长度为50 mm，共设定26个测点，测点间距为2 mm，将测得的数据通过MATLAB程序拟合出测量区域的波速与波传播云图，波速测量流程图如图16所示。经过测试，附加质量块的悬臂板与附加ABH的悬臂板初始固有频率分别为32.84和30.81 Hz（如表5所示），测试悬臂板凹口处的波速为1446和1443 m/s（如表6所示）。

最终附加质量块的悬臂板在振动540 min后，在根部出现了大裂纹，附加ABH的悬臂板在振动790 min后在悬臂板的凹口处出现了大裂纹，裂纹情况如图17所示。与仿真计算中应力最大处位置相对应。

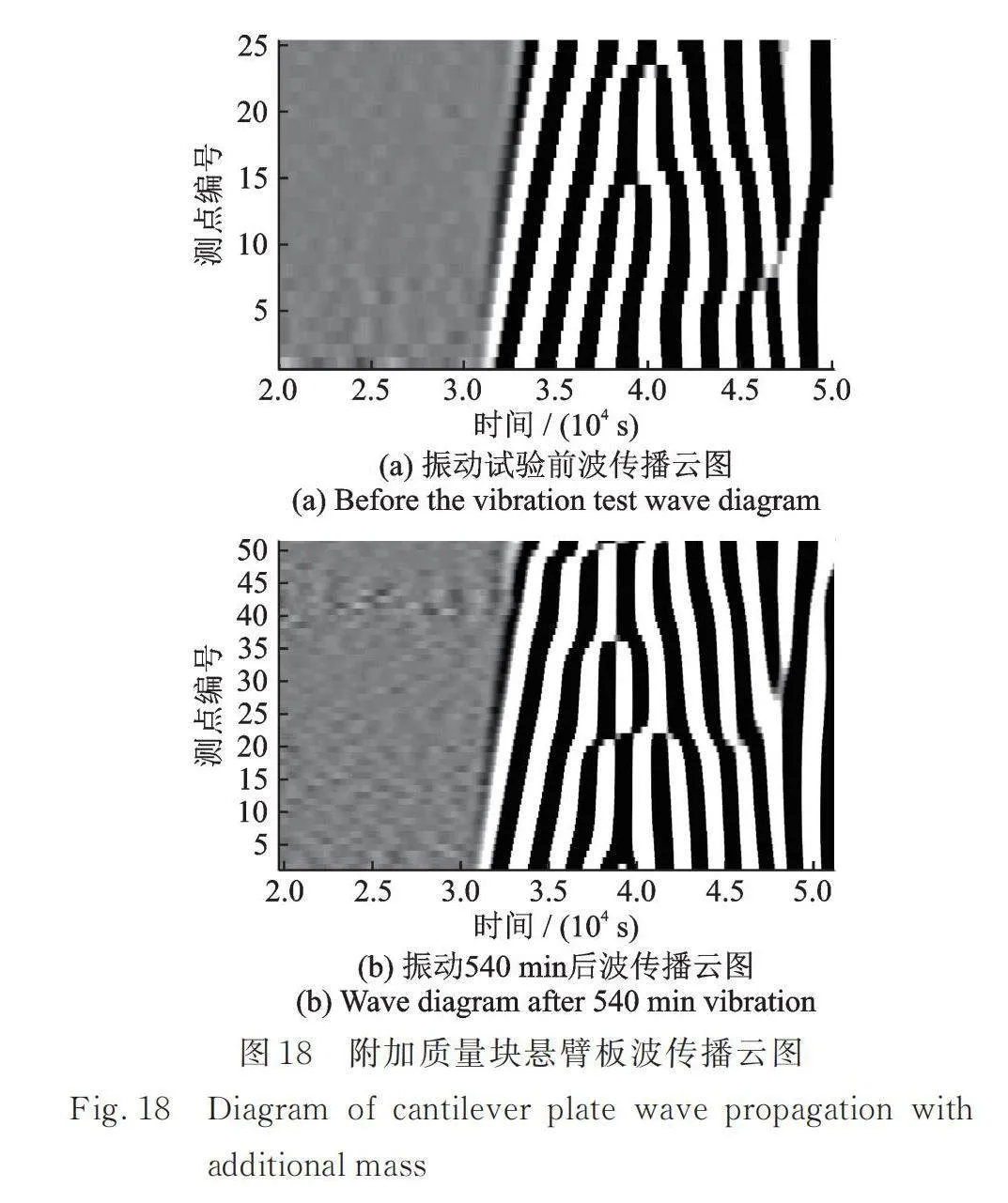
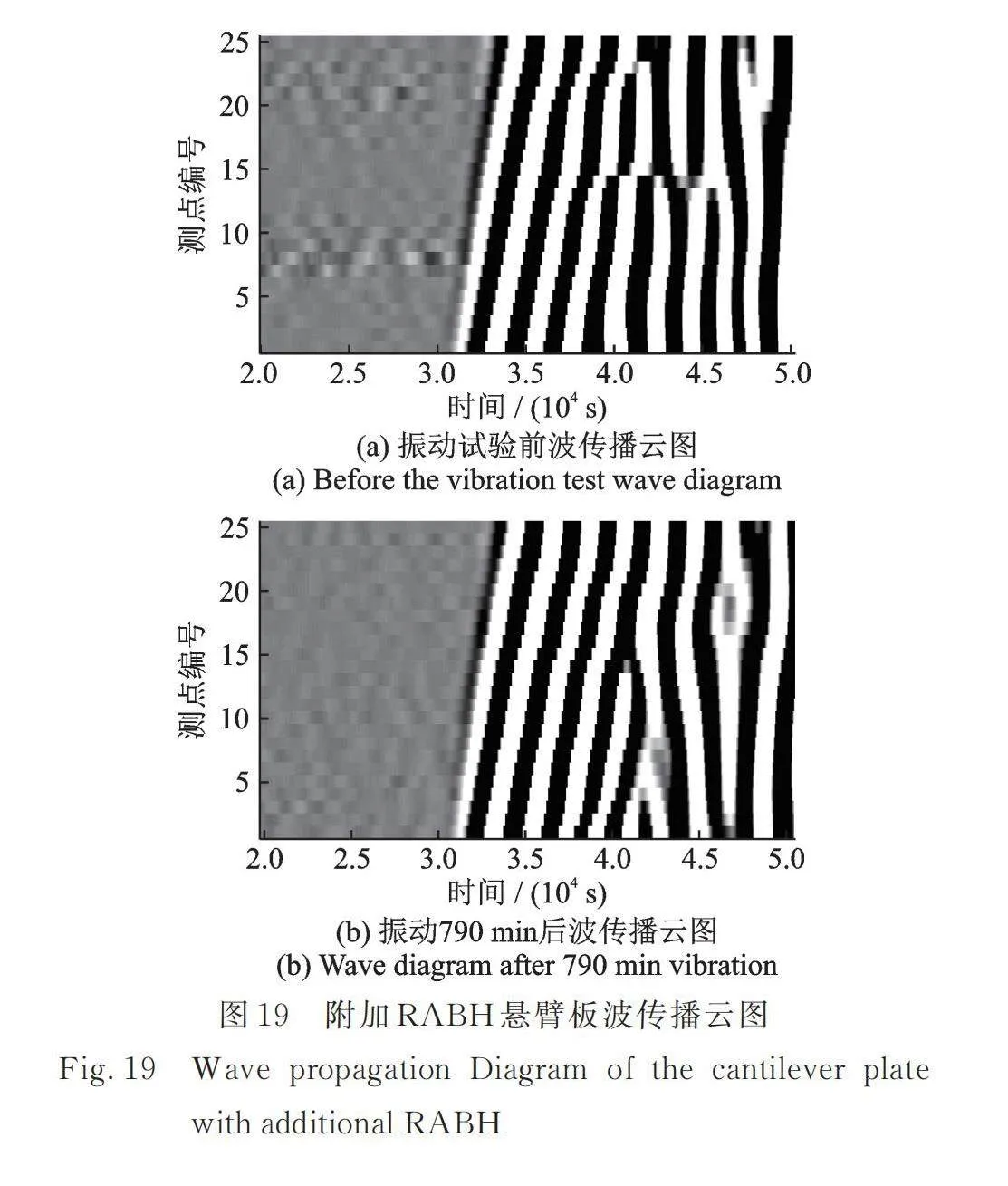
在出现裂纹后，两种悬臂板的固有频率分别变为19.9和24.93 Hz。波速也同样有着明显的下降，如表6所示，结合裂纹出现位置和波的传播云图可以看到，附加质量块的悬臂板的波速在靠近根部的位置有着明显的下降，因为振动540 min后由于根部出现的大裂纹对波速影响较大，现有的25个测点会出现数据不连续等情况，因此将振动540 min后的悬臂板测点增加1倍至51个测点，测试区域长度不变，依旧是50 mm，这样每两个测点的间隔为1 mm。计算初始与产生裂纹后的波速如表6所示，发现波速有所下降，但是下降的幅度并不大。观察如图18和19所示的初始与产生裂纹后的波传播云图，相比于初始情况，产生裂纹后的云图可以看到有部分弯曲出现。附加质量块的弯曲出现在后40%测点附近，附加RABH的弯曲出现在中间40%～80%测点附近，这与实际裂纹产生位置相对应。取附加质量块初始状态下、产生裂纹后的后40%点以及附加RABH初始状态下、产生裂纹后的中间40%～80%测点计算波速比较，如表6所示，附加质量块的悬臂板出现裂纹后的波速有着16%的下降。而附加RABH的悬臂板有着11.3%的波速下降。综合以上数据可以证实两块悬臂板均已达到疲劳失效状态。

由以上数据可以判断，本次试验中附加质量块的悬臂板振动540 min之后在根部发生疲劳失效，附加RABH的悬臂板在振动790 min后在凹口处发生疲劳失效。将振动时间换算成秒，并与两种结构的中心振动频率相乘得到载荷循环次数如表7所示，附加RABH后悬臂板的振动疲劳寿命延长了41.77%。

综上所述，本次试验结果表明，添加声学黑洞之后，主结构在共振时的动态响应减小，从而导致结构危险点处的应力有所下降。因此在不改变主结构刚度强度的条件下，可以有效延长结构的振动疲劳寿命。验证了RABH对于悬臂板结构有着明显的振动寿命延长效果。

试验中附加RABH虽取得了寿命延长的效果，但与预期尚有差距。主要原因分析如下：附加RABH在振动第690 min时发生断裂，那么至少在RABH开始产生疲劳到断裂的这一段时间内，附加结构对悬臂板应力的削弱作用失效了，导致损伤在这一段时间内快速累积，加快了悬臂板疲劳失效。这也指明了ABH吸振器下一阶段的研究重点应转向对其自身疲劳寿命的研究，以更安全可靠地投入工程使用。

2.3 RABH自身振动疲劳寿命探索

在上一节中提到过关于附加RABH之后，整个系统的最大应力转移到了RABH上，这样就有可能导致RABH的寿命要小于悬臂板的寿命。在实际试验中，附加RABH的悬臂板系统在振动到690 min时，RABH产生了疲劳破坏，载荷循环次数为1167480，发生破坏的位置在最长的一条斜边上，查看仿真结果可以发现，仿真中的应力最大处与实际疲劳破坏发生处位置一致，如图20所示。

参考试验中附加质量块的悬臂板疲劳寿命与附加RABH的悬臂板疲劳寿命，RABH自身的1167480次循环的寿命位于两者中间。虽然其寿命大于附加质量块时的悬臂板寿命，但其无法覆盖其附加的悬臂板的完整寿命周期，在实际使用中就会带来一些安全隐患，这为今后ABH的结构设计提出了更多需要考虑的因素，ABH大多工作于振动环境下，因此ABH本身也面临着严峻的疲劳问题。本文提出了简单估算ABH自身应力水平的方法，并通过试验验证了ABH的疲劳发生点与其仿真中应力最大处相对应，为今后ABH的设计提供了了一定的参考。

3 结 论

本文分别对悬臂板附加质量块与附加RABH的情况进行了振动分析与疲劳分析，得到以下结论：

（1）通过仿真计算以及试验验证，在共振状态下，附加RABH的悬臂板会比附加质量块的悬臂板拥有更低的动响应以及应力水平。在不改变悬臂板结构刚度和强度的前提下，理论上可以延长悬臂板的振动疲劳寿命。

（2）通过振动疲劳试验，验证了RABH对主结构有着明显的振动疲劳寿命延长的效果，相比于附加质量块，附加RABH的悬臂板的振动疲劳寿命有40%左右的增加。展现了通过附加ABH实现结构振动疲劳寿命延长的良好应用前景。

（3）探究了RABH自身的振动疲劳寿命与主结构疲劳寿命的关系，通过仿真计算和试验，目前RABH的工作寿命都无法覆盖悬臂板的振动疲劳寿命，对ABH在实际工程使用上有一定的影响。因此需要对RABH如何提升自身工作寿命做进一步研究。本文提出了简单估算ABH自身应力水平的方法，为今后ABH结构设计提供一定的参考。

参考文献：

［1］刘文光，陈国平，贺红林，等. 结构振动疲劳研究综述［J］.工程设计学报，2012，19（1）： 1-8.

Liu Wenguang，Chen Guoping，He Honglin，et al. Review of studying on vibration fatigue［J］. Chinese Journal of Engineering Design，2012，19（1）： 1-8.

［2］周凌波. 航空典型结构件的随机振动疲劳寿命分析［D］.南京： 南京航空航天大学，2014.

Zhou Lingbo. Random vibration fatigue life analysis of aircraft typical structures［D］. Nanjing： Nanjing University of Aeronautics and Astronautics，2014.

［3］徐志刚，陈荣，李权，等. 某型飞机进气道在噪声环境中的振动疲劳分析［J］. 装备环境工程，2011，8（4）： 100-103.

Xu Zhigang，Chen Rong，Li Quan，et al. Vibration fatigue analysis of plane inlet channel under noisy environment［J］. Equipment Environmental Engineering，2011，8（4）： 100-103.

［4］王明珠. 结构振动疲劳寿命分析方法研究［D］. 南京： 南京航空航天大学，2009.

Wang Mingzhu. Research on life analysis method for structure vibration fatigue［D］. Nanjing： Nanjing University of Aeronautics and Astronautics，2009.

［5］姚卫星. 飞机结构疲劳寿命分析的一些特殊问题［J］. 南京航空航天大学学报，2008，40（4）： 433-441.

Yao Weixing. Some special subjects of fatigue life prediction on aircraft structures［J］. Journal of Nanjing University of Aeronautics and Astronautics，2008，40（4）： 433-441.

［6］姚起杭，姚军. 工程结构的振动疲劳问题［J］. 应用力学学报，2006，23（1）： 12-15.

Yao Qihang，Yao Jun. Vibration fatigue in engineering structures［J］. Chinese Journal of Applied Mechanics，2006，23（1）： 12-15.

［7］何丁妮，廖云飞，崔韦，等. 不同疲劳加载方法对金属悬臂梁性能影响的试验研究［J］. 实验力学，2022，37（3）： 430-438.

He Dingni，Liao Yunfei，Cui Wei，et al. Experimental study on effect of different fatigue loading method on performance of metal cantilever beam［J］. Journal of Experimental Mechanics，2022，37（3）： 430-438.

［8］Mironov M A. Propagation of flexural wave in a plate whose thickness decreases smoothly to zero in a finite interval［J］. Soviet Physics-Acoustics，1988，34（3）：318-319.

［9］Krylov V V，Shuvalov A L. Propagation of localised flexural vibrations along plate edges described by a power law［J］. Institute of Acoustics，2000，22（2）： 263-270.

［10］Krylov V V. New type of vibration dampers utilising the effect of acoustic black holes［J］. Acta Acustica United with Acustica，2004，90（5）： 830-837.

［11］Mironov M A，Pislyakov V V. One-dimensional acoustic waves in retarding structures with propagation velocity tending to zero［J］. Acoustical Physics，2002，48（3）： 347-352.

［12］Krylov V V，Tilman F J B S. Acoustic ‘black holes’ for flexural waves as effective vibration dampers［J］. Journal of Sound and Vibration，2004，274（3-5）： 605-619.

［13］Deng J，Guasch O，Maxit L，et al. Vibration of cylindrical shells with embedded annular acoustic black holes using the Rayleigh-Ritz method with Gaussian basis functions［J］. Mechanical Systems and Signal Processing，2021，150： 107225.

［14］Ji H L，Wang N，Zhang C，et al. A vibration absorber based on two-dimensional acoustic black holes［J］. Journal of Sound and Vibration，2021，500： 116024.

［15］Ji H L，Zhao X N，Wang N，et al. A circular eccentric vibration absorber with circumferentially graded acoustic black hole features［J］. Journal of Vibration and Acoustics，2022，144（2）： 021014.

［16］Ji H L，Liang Y K，Qiu J H，et al. Enhancement of vibration based energy harvesting using compound acoustic black holes［J］. Mechanical Systems and Signal Processing，2019，132： 441-456.

［17］何璞，王小东，季宏丽，等. 基于声学黑洞的盒式结构全频带振动控制［J］. 航空学报，2020，41（4）： 223350.

He P，Wang X D，Ji H L，et al. Full-band vibration control of box-type structure with acoustic black hole［J］. Acta Aeronautica et Astronautica Sinica，2020，41（4）： 223350.

［18］Deng J，Gao N S，Chen X. Ultrawide attenuation bands in gradient metabeams with acoustic black hole pillars［J］. Thin-Walled Structures，2023，184： 110459.

［19］Sheng H，He M X，Ding Q. Vibration suppression by mistuning acoustic black hole dynamic vibration absorbers［J］. Journal of Sound and Vibration，2023，542： 117370.

［20］Zhou T，Cheng L. Planar swirl-shaped acoustic black hole absorbers for multi-directional vibration suppression［J］. Journal of Sound and Vibration，2022，516： 116500.

［21］Deng J，Chen X，Yang Y，et al. Periodic additive acoustic black holes to absorb vibrations from plates［J］. International Journal of Mechanical Sciences，2024，267： 108990.

［22］Du W Q，Li S X，Luo Y X. A frequency domain method for vibration fatigue analysis of acoustic black hole structure［J］. International Journals of Fatigue，2023，172： 107605.

Study on the effect of additional acoustic black hole on vibration life of cantilever plate

ZOU Yu-qi1，ZHU Shen-yan1，WANG Chao-yan1，2，TAO Chong-cong1，ZHANG Chao1，WU Yi-peng1，JI Hong-li1，QIU Jin-hao1

（1.State Key Laboratory of Mechanics and Control for Aerospace Structures，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，China； 2.Nanjing Institute of Information Technology，Nanjing 210016，China）

Abstract： The fatigue failure of the structure under vibration conditions has brought hidden dangers to its own service life and the personal safety of the user. At present，there are solutions for the structural vibration fatigue such as adding reinforcement bars and laying a large amount of damping materials，but the efficiency is often low and the additional mass is excessive. In order to solve the above problems，an additional acoustic black hole （ABH） is installed on the structure to reduce the stress amplitude and extend the service life by reducing the structural response. Using a cantilever plate as the reference structure，the steady state dynamics analysis is carried out by the finite element method. The results show that the stress response at the gap of cantilever plate is significantly reduced after the addition of rectangular acoustic black hole （RABH）. Through stress and fatigue experiments，it is verified that additional RABH can reduce the stress response at the dangerous point of the structure and extend the vibration fatigue life of cantilever plate structure.

Key words： acoustic black hole；cantilever plate；vibration fatigue

作者简介： 邹宇琪（1999―），男，硕士研究生。E-mail： 490297036@qq.com。

通讯作者： 季宏丽（1983―），女，教授，博士生导师。E-mail： jihongli@nuaa.edu.cn。