结构动载荷识别研究进展
2024-10-24姜金辉张方









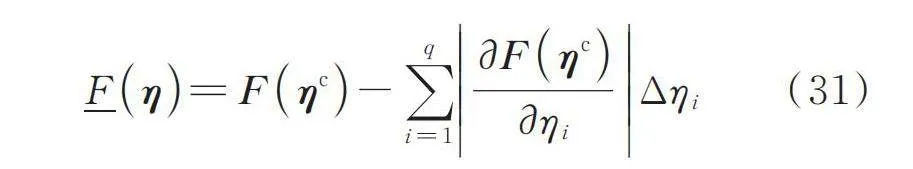







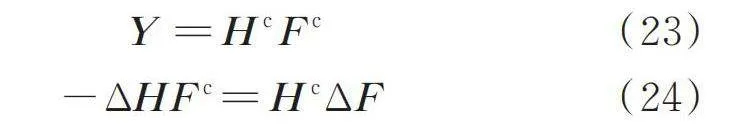


























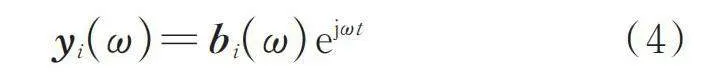

摘要: 作用于工程结构上的动载荷由于环境等限制难以通过直接测量的方式获取,基于动响应信息间接识别或重构动载荷已成为一种十分有效的途径。动载荷识别经过数十年的发展,已经形成了一系列行之有效的方法。本文总结了动载荷识别方法的研究历程及主要成果,系统性阐述了典型时、频域方法以及基于函数拟合思想、正则化策略、贝叶斯框架、数据驱动等动载荷识别方法,并讨论了各方法的优缺点以及适用范围。此外,还针对载荷识别过程中普遍存在的结构参数不确定问题以及输入条件不确定问题进行了总结。动载荷位置识别也是动载荷识别问题的重要组成部分,本文对现有位置识别方法进行了归纳分析。探讨了动载荷识别方法的工程应用,并分析了现有方法的局限性。结合当前实际工程应用中日益迫切的需求及动载荷识别领域面临的问题,展望了未来动载荷识别亟需攻克的技术难题以及可能的发展方向和重点领域。
关键词: 动载荷识别; 数据驱动; 不确定性; 位置识别; 工程应用
中图分类号: O327; TB123 文献标志码: A 文章编号: 1004-4523(2024)10-1625-26
DOI:10.16385/j.cnki.issn.1004-4523.2024.10.001
1 概 述
在当前工程和科技领域中,各种装备和结构存在着大量的振动问题,由振动引起的结构的安全性、可靠性等问题成为被关注的焦点。解决振动问题首先要对振动溯源,然而,大多数情况下,工程上很难或无法直接测定结构上的振源(即所作用的外载荷)。如图1所示的高层建筑受到的风雨载荷、火箭发射时外部脉动压力、水下推进器对舰体结构的动载荷等,这些因强风、强流、水流以及波浪等作用而施加到结构上的动载荷,通常很难被直接测量或者无法测量。确定实际工况下结构的振源是振动工程中最棘手的问题之一,在这个背景下,动载荷识别以其独特的研究思路成为确定工程结构和装备外载荷的一种重要手段。
动载荷识别(或重构、反演)的基本原理是根据实测的结构系统动态响应和已知结构系统的动态特性,反演作用于结构系统的动态激励,属于结构动力学的第二类逆问题,是数学中典型的源识别反问题[1]。动载荷识别涵盖动载荷位置识别以及动载荷幅值重构;前者是指确定动载荷在结构上作用的位置,后者是指确定动载荷在时域或者频域内的幅值。动载荷识别旨在基于响应和动力学模型反演分析结构受到的外部载荷,揭示载荷变化对结构系统的影响,从而为动力学分析、控制及设计提供重要依据,确保工程结构设计的可行性、安全性、可靠性、舒适性。动载荷识别是结构动力学重要的研究方向,也是一个涉及动力学、测试技术、信号分析以及计算数学等多学科的重要研究领域。
动载荷识别技术最早可以追溯到20世纪70年代,源自于航空工业,用于研究直升机旋翼桨毂中心的动载荷。至今,动载荷识别已发展近50年,吸引了越来越多的学者从事该领域的研究,也形成一些经典的算法和理论,促进了航空航天领域结构动力学的发展,该技术也被推广应用至交通运输、建筑结构、防风抗灾、健康监测等工程领域。动载荷识别的不断发展不仅使工程结构具备更高水平的安全性和可靠性,同时也为国家重大装备系统的研制赋能,推动大型复杂结构动力学设计水平的不断提升。
本文总结归纳动载荷识别的研究成果,分析当前动载荷识别领域面临的挑战和问题,探讨动载荷识别在工程上的应用可能性及目前的局限性,并展望动载荷识别技术的未来发展方向。通过全面了解动载荷识别技术的发展,有望更好地实现其在工程实践、科学研究和创新领域中的潜在应用。
2 动载荷识别研究历程及成果
动载荷识别技术起源于1979年,最初应用于航空工业,获取频域内结构加速度响应与载荷之间的频响函数矩阵[2],并通过直接求逆的方式完成未知动载荷识别。但是这一类频域动载荷识别方法在结构固有频率附近识别精度较差;此外,该方法受限于信号采样时长,难以对冲击载荷等瞬时载荷进行识别。因此,研究者们利用未知激励与结构动响应之间的时序卷积关系,提出了时域动载荷识别方法。20世纪90年代,随着动载荷识别技术发展的不断深入,针对复杂连续结构的动载荷识别成为研究热点,基于模态坐标变换将连续结构离散化的动载荷识别方法应运而生[3]。21世纪以来,动载荷识别技术的发展也进入“快车道”,逐渐突破传统动力学领域,与信号处理、数理统计等领域不断融合,形成了诸如基函数拟合、卡尔曼滤波等一系列动载荷识别方法。随着动载荷识别技术的应用日益广泛,研究对象也从单点、多点集中载荷向分布动载荷过渡;另外,为了降低动载荷识别过程中的不适定性,一系列基于正则化思想[4]的动载荷识别方法得以飞速发展,这些方法有效地提升了动载荷识别的稳定性。随着计算机技术的发展,无需掌握结构动特性的基于数据驱动策略的动载荷识别方法也逐渐成为了研究热点。
为了进一步满足工程中对于动载荷识别精度与效率的需求,针对工程结构中存在难以避免的不确定性,研究人员引入不同的假设并提出相应的动载荷识别方法,进一步提升了动载荷识别技术的工程应用可行性;动载荷识别技术仍在不断完善更新,动载荷识别方法的发展历程如图2所示。
本节从典型的时域、频域动载荷识别方法出发,依次阐述基于基函数拟合、正则化策略、贝叶斯框架、数据驱动的动载荷识别方法,介绍动载荷识别中的两类不确定性问题以及动载荷位置识别的研究进展,并对研究现状及典型成果进行归纳总结,如图3所示。
2.1 典型的时、频域动载荷识别方法
经过多年的不断发展,已经形成了许多典型的动载荷识别方法,主要包括两大类:一类是频域方法,以直接求逆法、逆虚拟激励法、模态叠加法等为代表;另外一类是时域方法,典型代表包括传统积分法、时域迭代法和Green核函数方法等,如图4所示。
频域方法将时域信号进行傅里叶变换,得到幅频特性曲线,该方法对样本长度有一定要求,适用于长时或平稳载荷识别。频响函数直接求逆法源于航空领域,Bartlett等[2]根据加速度响应对直升机桨毂中心的动载荷进行了识别;Giansamte等[5]根据加速度响应和传递函数矩阵对AH‑1G直升机飞行时主轴和尾桨受到的动载荷进行了识别。频响函数直接求逆法简单易实施,但Starkey等[6]研究发现这种方法的抗干扰能力较差,尤其是对固有频率附近的载荷识别结果较差。Karlsson[7]发现频响函数矩阵的逆运算对响应测量噪声和模型误差高度敏感,会严重影响载荷识别结果的稳定性。
根据频响函数直接求逆法,识别确定性载荷的表达式为:
(1)
式中 为待识别的频域内的动载荷列阵;为频响函数矩阵的广义逆;为频域内的动响应列阵。
识别随机载荷的表达式为:
(2)
式中 为待识别的激励功率谱密度矩阵;为动响应的功率谱密度矩阵;和分别为频响函数矩阵的共轭和转置。
为减小随机载荷识别的计算量,Lin等[8]将虚拟激励法进行逆向推广,提出了适用于平稳随机载荷识别的逆虚拟激励法。针对随机载荷识别中的病态逆问题,姜金辉等[9]提出一种条件数权重法。Jia等[10]综合分析了响应测量误差和频响函数误差对随机载荷识别结果的影响,分别提出加权正则化方法和加权总体最小二乘法。逆虚拟激励法的具体理论如下:
(3)
构造虚拟响应:
(4)
认为虚拟响应由虚拟激励产生:
(5)
识别激励功率谱密度矩阵:
(6)
式中 r为响应功率谱密度矩阵的秩。
时域法相较频域法起步较晚,但针对冲击载荷、非平稳载荷的识别具有较大优势,并且对较短时间样本的识别也具有优势,大部分传统时域方法的思路是基于结构外部激励与动响应之间的时序卷积关系来重构动载荷。Hollandsworth 等[11]利用时域卷积法,将试验采集到的加速度数据积分为速度数据,成功识别出作用在结构上的冲击载荷。赵凤遥等[12]将动载荷在微小的时间单元中视为线性力,利用Duhamel积分推导了待识别外载荷的识别公式,该方法结合了多种类型的动响应组合进行载荷识别,算例表明了该方法的可行性。胡杰等[13]将Duhamel积分离散化,提出了基于传递函数矩阵的动载荷识别方法。此外,研究人员在直接积分的基础之上提出了一种基于精细积分思路的动载荷时域识别方法。文祥荣等[14]、王静等[15]基于精细逐步积分法重构了作用在比例阻尼系统的动载荷时间历程,并结合数值仿真验证了该方法的可行性与精度。此外,王淑娟等[16]对精细积分法进行改进,结合二阶系统解耦进一步提高了时域动载荷识别的精度。
除传统时域积分方法之外,在结构动力学计算中,Newmark‑β算法、Wilson‑θ算法是计算正问题的一类重要的数值迭代计算方法,在一定的条件下可保证算法的稳定性[17]。诸多学者提出了基于Newmark‑β和Wilson‑θ算法的动载荷识别时域迭代算法。Newmark‑β方法最早的研究对象是多自由度离散系统。Kortis等[18]构建了桥梁的有限元模型,成功应用Newmark‑β方法识别车‑桥接触载荷。Liu等[19]推导了基于显式Newmark‑β的动载荷识别方法,采用多自由度系统作为仿真算例验证了该方法的精度。随着研究的进一步深入,一些学者也提出了将Newmark‑β方法应用于连续系统。Jiang等[20]基于模态坐标变换将连续系统解耦为多自由度系统,应用Newmark‑β法获得载荷与响应显式的卷积表达式,结果表明该方法具有较好的稳定性和抗噪性。Wilson‑θ法同样是一种数值迭代积分算法,具有直观、高精度等优点[21]。Wilson‑θ方法的基本思想与Newmark‑β方法类似,都是将时间离散化,根据t时刻的响应对t+Δt时刻的响应进行计算。所不同的是,Wilson‑θ法引进参数θ,将假设的加速度线性变化范围由[t,t+Δt]扩大到了[t,t+θΔt]时间段。陈英华[22]推导了基于Wilson‑θ方法的动载荷识别方法,并通过仿真算例验证其效果。诸多学者也针对Wilson‑θ方法的载荷识别精度开展了相关研究。姜金辉等[17]对比分析了Wilson‑θ方法中的时间间隔、测点数目及位置等因素对识别结果的影响,最后引入黄金分割法改善载荷识别算法的累计误差。徐菁等[23]利用二分法迭代修正Wilson‑θ方法的动载荷识别结果,提高了Wilson‑θ算法的稳定性及抗噪性能;此外,使用拟静态初值法获取Wilson‑θ算法初值,进一步提高了识别精度[24]。以Newmark‑β和Wilson‑θ等算法为代表的时域迭代动载荷识别方法具有思路清晰、易于编程实现的特点。这一类动载荷识别算法都可以分成显式和隐式两种形式。隐式动载荷识别算法存在累计误差,随着分析时间的增长,识别结果有可能发散。显式动载荷识别算法虽然没有累计误差,但在计算过程中涉及大维度矩阵求逆,容易出现矩阵病态问题,造成识别误差。
在线性时不变假设下,对时域上响应与载荷之间的卷积关系进行离散,即可得到脉冲核函数矩阵,从而建立载荷识别正问题。目前,Green函数是最常用的一种脉冲核函数。Wu等[25]提出两种识别冲击载荷的方法,第一种方法基于Green函数,第二种方法基于试验,不涉及Green函数,两种方法的识别结果一致良好。韩旭等[26]分别基于Green脉冲函数和Heaviside阶跃函数建立了载荷识别正问题,并采用三种不同的正则化方法处理反问题,对某车型引擎盖上作用的正弦载荷和三角载荷进行了识别。缪炳荣等[27]基于Green函数对不同正则化方法处理病态问题的结果进行了分析。孔帅等[28]基于Green函数对船体结构上冲击冰载荷的识别进行了研究。Liu 等[29]、He等[30]、Wu等[31]基于Green函数对不确定性结构动载荷识别方法进行了研究。Green函数简化了时域上复杂的卷积关系,但是也存在着严重的不适定性问题。
2.2 基于函数拟合思想的动载荷识别方法
基函数拟合的本质是通过已知的基函数最大程度上拟合逼近目标函数或者数据,是信号处理、数据拟合分析、图像处理等方面的得力工具。将基函数拟合法引入动载荷识别,把动载荷基于基函数进行展开,将动载荷的识别转化为基函数系数的识别,进而根据识别出的基函数系数重构作用于结构上的动载荷。常见的基函数拟合法有:冗余字典法、径向基函数法、小波变换法、广义正交多项式法等。
冗余字典法利用过度完备的基函数集合,更加灵活地表达各种信号,其选取的基函数不必满足正交性。但是,冗余字典法通常包含大量的基函数,这导致未知数的数量增多进而计算难度增大,并且对于不同的载荷情况,可能需要先验知识或反复试验。Liu等[32]提出了一种基于压缩感知和冗余字典的移动力识别方法,其识别流程图如图5所示。该方法可以有效缩短采集数据的样本长度,同时提高移动力识别的准确性,增强抗噪性,实现载荷识别精度和识别效率的平衡。Pan等[33]研究了包含缓变谐波和冲击载荷的复杂移动力识别问题,提出一种基于加权L1范数正则化和冗余级联字典的混合移动力识别方法,来解决传统单一基函数集无法对移动力进行稀疏表示的问题,该法准确性高,噪声鲁棒性强,并可准确获取移动力的局部冲击信息。何文博等[34]针对噪声对复杂动载荷识别精度影响大等问题,提出了一种基于冗余扩展余弦字典的L1范数正则化识别法,该法对拍频载荷与连续冲击载荷的表示具有较高的稀疏性,提高了复杂载荷在不同噪声水平下的载荷识别精度,其抗噪性能优于传统正则化方法。
径向基函数通常指一类基于径向对称的数学函数,可高效地处理多元问题,计算中储存方便、运算简单,在载荷识别领域可减小核矩阵规模,改善病态性。池林等[35]指出现有时域识别法大多基于单位脉冲函数或阶跃函数近似,这导致计算的离散时间间隔显著影响病态程度,为此提出了基于径向基函数的时域动载荷识别法以有效减小矩阵病态性。
小波变换通常指使用小波函数,即具有短时窗口的波形,对信号进行变换,它发展了短时傅里叶变换局部化的思想。其时间窗可时变,具有对频域辨识能力强的优点,利用小波变换可提升抗噪性能,提升动载荷识别精度。Wang等[36]针对时域卷积积分的不稳定性问题,提出了多自由度系统动载荷识别的小波‑模态复合变换方法,提高了计算效率,增强了识别抗噪性能。Li等[37]针对逆傅里叶变换的局限性以及载荷识别过程中的病态性等问题,提出一种基于小波多分辨率的载荷识别法,以及影响该方法精度的参数定性和定量规则,通过数值仿真验证了该方法在载荷识别精度方面的优势。Lu等[38]利用小波尺度函数和最小二乘时元法提高了识别精度,利用最小二乘运算中的积分过程提高了抗噪性能。
上述研究主要是针对集中动载荷,事实上,分布动载荷在时间域与空间域两个维度连续分布,基函数拟合思想更适用于分布动载荷识别。分布动载荷时空特性使得分布动载荷识别相对于集中动载荷识别的未知参数更多,难度也更大。目前,分布动载荷识别主要是利用基函数拟合思想将时间维度和空间维度分别离散,实现降维。
Karlsson[7]讨论了空间分布形式已知、幅值大小未知的分布简谐力的动载荷识别情况,研究的重点在于线性系统简谐外力与结构上响应之间的灵敏度分析。Granger等[39]针对未知空间分布形式的随机动载荷识别,基于各阶振型函数将复杂的分布随机动载荷时域历程进行广义傅里叶展开,并结合模态坐标变换法及正则化算法,在频域内建立了激励互功率谱密度的识别模型。张方等[40]提出了级数系数平衡法,通过幂级数展开构建了分布动载荷识别模型。为提高分布动载荷的识别精度,张方等[41]提出利用切比雪夫正交多项式叠加拟合载荷的空间分布,完成了频域内一维分布动载荷的识别,随后进一步研究该方法在二维分布动载荷识别问题上的可行性,并通过仿真算例和试验讨论了该方法的识别精度。姜金辉[42]利用勒让德正交多项式,分别开展了一维梁结构以及二维薄板结构的平稳分布随机动态载荷识别,并通过仿真与结构的风洞试验进行了验证。Li等[43]提出了一种基于Green函数和切比雪夫正交多项式的分布动载荷识别方法,分别识别了时间历程以及空间分布函数。Wang等[44]根据切比雪夫多项式和泰勒展开的区间分析法,采用加速度响应作为观测信号对未知结构系统上的分布载荷进行识别,并验证了该方法的有效性和精度,其识别流程如图6所示。
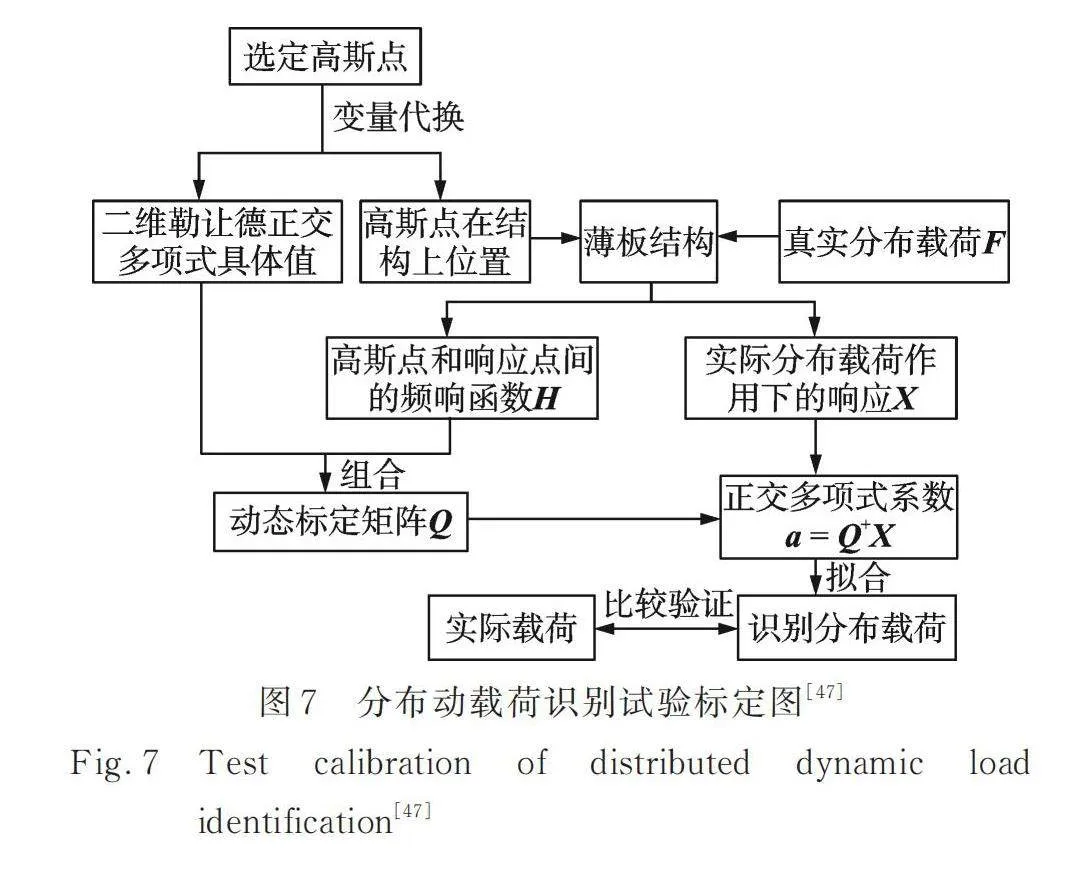
在传统的分布动载荷识别技术中,一般通过建立有限点的结构动响应信息与表征分布动载荷的有限维特征之间的传递特性关系来完成识别,确定该传递特性关系是重构分布动载荷的一个重要环节,亦即动态标定过程[45]。姜昊[46]利用切比雪夫多项式完成了非接触分布激励的动态标定,将有限元仿真动态标定应用到载荷识别中,开创了一种新思路。然而,传统的仿真动标定方法基于有限元模型实现,存在模型误差,进而使得动标定矩阵存在偏差,最终导致分布动载荷的识别误差。为解决传统动标定方法的局限性,Jiang等[47]针对分布动载荷识别过程中传统动标定方法存在模型误差的问题,基于勒让德正交多项式和高斯积分提出了一种新的试验动标定方法,如图7所示,解决了传统方法中模型误差导致载荷识别结果不精确的问题,有效提升了分布动载荷的识别精度。除广义正交多项式拟合方法外,学者们还研究了其他分布动载荷识别方法,如小波变换[48] 、虚拟场法[49]、样条插值法[50]、盲源分离技术[51]、子区域插值技术[52]等。
分布动载荷识别的研究总体而言仍处于基础阶段,依然面临很多问题及挑战,主要表现在:(1)分布动载荷分布特征及识别方法研究还不够充分;(2)分布动态载荷的测量和施加困难,工程上难以施加分布动态载荷以进行载荷识别验证;(3)分布动载荷随时间、空间连续变化,识别的未知参数更多,识别难度也更大;(4)分布动载荷识别的不适定问题比集中动载荷识别更为严重。由此可见,分布动载荷识别方面的研究仍是动载荷识别领域内亟需解决的重要问题之一。
2.3 基于正则化策略的动载荷识别方法
在动载荷识别这一反问题的研究过程中,不适定性问题尤为突出。数学上不适定性是指方程解不满足存在性、唯一性和稳定性三个条件中的一个,动载荷识别问题中不适定性的典型特征是解的不稳定性。对于下式描述的动载荷识别系统模型:
(7)
已知结构响应向量y和系统矩阵H,反求载荷向量f需要对系统矩阵进行求逆运算。当系统矩阵的条件数过大时,求解出的载荷向量f并不满足稳定性。若响应y中含有微小噪声,或系统矩阵H存在误差,则会导致识别载荷的误差变得很大,因此直接求逆的方式不能得出准确的载荷。
正则化方法是改善不适定性问题的有效方法,其基本思想是通过施加合理的附加条件或边界约束,求解不适定问题的正则化解,然后从这些解中挑选最适合方程的解。
载荷识别中经典的正则化方法主要有截断奇异值分解法(TSVD)和Tikhonov法。截断奇异值分解法由奇异值分解法发展而来,如下式所示:
(8)
式中 和为由左右奇异值向量构成的正交矩阵;为矩阵的奇异值。
将奇异值按照从大到小的顺序排列,并设置阈值,使得矩阵奇异值满足以下关系:
(9)
用截断奇异值分解法求得解为:
(10)
梅立泉等[53]引入TSVD正则化方法处理反问题的不适定性,对不同噪声的实测响应进行了面载荷的反演求解,算例表明,TSVD正则化方法对响应误差的适应性强,识别精度高。但是截断奇异值分解法在动载荷识别上存在一些不足,如识别精度受测量噪声、响应类型及数量影响较大。因此,Zhen等[54]基于TSVD和广义奇异值分解(GSVD)正则化技术,提出了一种截断广义奇异值分解(TGSVD)正则化方法用于识别动态轴载荷,仿真结果表明,TGSVD与传统方法相比精度更高、适应性更好、抗噪性更强。
Tikhonov正则化方法于20世纪40年代由前苏联院士Tikhonov提出,主要思路是将原始问题的求解转化为一个最优化问题,如下式所示:
(11)
式中 表示正则化参数。
通过求解该问题可以获得Tikhonov正则化解:
(12)
式中I为单位矩阵。
Fan等[55]改进了Tikhonov正则化方法,提出了一种改进的正则化算法(IRA),在对四自由度振动系统的数值模拟研究中,结合Tikhonov正则化方法,讨论了采样频率和噪声水平对IRA正则化参数的影响。最后,对悬臂梁在冲击和谐波载荷作用下进行了实验,验证了IRA的优势。
对比上述正则化方法,迭代正则化方法可以处理更大规模的不适定问题,其基本原理是通过迭代逐步逼近真实的解,在每次迭代中,将正则化项添加到目标函数中,以帮助控制解的稳定性和精度。常用的迭代正则化方法有牛顿迭代法、Landweber迭代法、共轭梯度法和最小二乘法等。Wang等[56]在新的迭代正则化算子的基础上,提出了一种新的快速收敛迭代正则化方法,用于随机结构的动态载荷识别,并且通过数值算例验证了所提方法在随机结构参数下重构作用于工程结构的载荷的可行性和收敛性。在未来的研究中,这种新开发的迭代正则化算法可以应用于具有随机结构参数的航空结构分布式动载荷辨识。
近年来,也有学者将稀疏正则化方法用于动载荷识别问题中。稀疏正则化方法通过引入稀疏性约束,迫使解向量中尽可能多的元素为零,从而挖掘出数据中的重要特征[57]。Qiao等[58]提出了一种基于字典的通用稀疏正则化模型进行载荷辨识,发展了变量分离近似稀疏重构方法解决高噪声响应中的稀疏正则化问题,对悬臂薄板结构上的冲击力与谐波力进行识别,证明了基于稀疏正则化识别的结果是稳定和精确的。
在动载荷识别中,正则化参数的选取对于提高识别精度和稳定性非常重要。后验策略是一种常用的方法,它不需要提前知道数据集中的噪声水平和其他相关信息,而是通过使用训练好的模型和验证集来评估不同正则化参数的性能。在后验策略中常用的方法是广义交叉验证(GCV)和L曲线法。然而,在某些情况下,GCV函数曲线可能过于平坦,无法准确地找到最小值,L曲线法在动载荷识别中需要提前确定最优正则化参数的近似范围,如果无法准确地确定这个范围,可能会导致选择的正则化参数不够理想。Choi等[59]对普通交叉验证(OCV)、广义交叉验证(GCV)和L曲线准则的方法进行了比较,以应用于结构动力学的载荷识别,对比表明,L曲线法在高噪声情况下比OCV或GCV表现更好,但在噪声水平较低时表现较差。在实际应用中,正则化参数的选取仍没有统一的标准,研究者可以根据具体情况选择合适的后验策略或尝试多种策略相结合,在实践中不断优化正则化参数的选取策略。
2.4 基于贝叶斯框架的动载荷识别方法
贝叶斯方法是近几十年发展起来的数理统计的一个重要分支。其基本思想是:通过条件概率密度和假设的未知量的先验概率密度,利用贝叶斯公式求解后验概率,然后根据后验概率密度的大小对未知量进行估计。
贝叶斯基本公式是贝叶斯框架的核心。设和分别代表事件和事件,和分别代表其发生的概率,为和联合发生的概率,为在事件已经发生的条件下,事件发生的可能性。则贝叶斯公式如下:
(13)
若事件代表响应信息,事件代表参数,则贝叶斯公式可以改写为:
(14)
求解该模型的最大后验概率估计即可得到参数的估计值,即
(15)
贝叶斯理论这种由先验信息推导出后验概率的思想,与动载荷识别中由响应到载荷的逆向过程很相似,贝叶斯理论框架也被应用到动载荷识别中。经过多年的发展,形成了基于卡尔曼滤波的动载荷识别方法以及贝叶斯正则化方法等许多研究成果。
卡尔曼滤波(KF)方法是针对高斯型噪声、线性系统的一种特殊的贝叶斯方法。Kalman[60]最早提出了卡尔曼滤波方法,经过发展和完善,已被广泛应用于导航、载荷识别以及损伤识别等诸多工程领域中。卡尔曼滤波适用于线性高斯系统,其优势在于能充分考虑模型误差和测量误差,且是一种递归算法,运行效率很高。卡尔曼滤波理论本质是融合了预测结果和测量结果的系统状态估计,主要包含测量更新和状态更新两个过程。
(16)
(17)
式中 为先验状态向量;为后验状态向量;为测量响应;为卡尔曼滤波增益矩阵;和为状态更新方程中的参数矩阵;表示k时刻的激励载荷;和为测量更新方程中的参数矩阵。即根据当前时刻的观测值,对前一时刻的最佳估计作线性修正,得到当前时刻的最佳估计。
传统的卡尔曼滤波算法假定激励已知,估计状态向量。为了识别结构上的未知激励,常见的做法是在卡尔曼滤波识别系统状态的基础上,引入最小二乘方法识别动载荷[61];或者是将未知载荷视为状态向量的一部分,组成增强状态向量,使用卡尔曼滤波技术识别出此状态向量[62]。Jiang等 [63]使用卡尔曼滤波算法实现了动载荷的在线识别。杨智春等[64]注意到卡尔曼滤波算法需要合理选择权系数,并对现有系数选取方式进行总结,主要包含常系数、自适应权系数和智能模糊权系数的选取三种类型,并指出智能模糊权系数的收敛性更好。Saeed等 [65]参照卡尔曼滤波思想,分别针对状态估计和激励识别两个阶段提出了双卡尔曼滤波方法。该方法具有更好的低频抗漂移性能,但对激励的模型误差矩阵比较敏感,一旦参数设置不合理,载荷识别效果也不佳。梁忠仔[66]提出了一种改进的双卡尔曼滤波方法,并使用LabVIEW设计了一个动载荷在线识别系统,实现了对结构未知载荷的高效识别。
针对非线性系统的动载荷识别问题,研究人员分别提出了扩展卡尔曼滤波(EKF)和无迹卡尔曼滤波(UKF)。EKF算法通过计算每一个时刻的雅可比矩阵将非线性系统线性化,计算量较小,但只有一阶精度,适用于弱非线性结构。EKF算法需要计算一组Sigma采样点来解决强非线性问题,它能够达到泰勒级数展开的二阶精度,但计算量较大。
Ma等[67]基于EKF和递归最小二乘法(RLS)提出了一种估计非线性结构体系输入载荷的在线反演方法。谢丽宇等[68]基于EKF算法对非线性阻尼系统的未知动载荷进行识别,仿真算例表明该算法对非线性系统也适用。张肖雄等[69]将投影矩阵引入EKF算法进行载荷识别,通过分段线性结构和非线性 Duffing 系统验证了此方法的有效性。Guo等[70]基于改进UKF,开发了一种新的非线性结构载荷识别方法。王婷等[71]引入无迹变换改善了卡尔曼滤波算法的性能,使之能适用于非线性系统的载荷识别,具有至少二阶识别精度。
针对结构参数和载荷同时未知的情况,有学者提出将未知参数以及状态向量组成广义状态向量。此时系统的状态方程和测量方程均变成非线性方程,应用EKF算法和UKF算法,即可实现对系统状态、结构参数和未知载荷的联合识别。
Yang等[72]提出了自适应EKF算法,根据响应残差跟踪结构参数的变化情况。但该算法需要求解强非线性方程,不能满足在线识别要求。Lei等[73]简化了Yang等[72]提出的算法,分阶段识别出载荷和状态向量。该算法能同时识别结构未知参数和载荷,并且适用于非线性结构。Naets等[74]利用扩展卡尔曼滤波算法将结构状态向量、参数、激励组成一个增广向量,应用PBH准则判定系统的可观测性,并采用虚拟位移的概念稳定地识别出系统的增广向量,从而求得结构参数未知情况下的动载荷。黄丽媛[75]利用扩展卡尔曼滤波理论,分别对桥梁结构以及剪切型框架结构进行了参数识别和动载荷识别。
Ding等[76]提出了约束UKF方法,将动荷载识别问题转化为多项式系数的识别。该方法能同时识别结构参数和外部激励,但需识别的未知参数数量较多,导致计算效率不高。Al‑Hussein等[77‑78]提出了基于无迹卡尔曼滤波的两阶段识别方法,首先利用最小二乘算法估计未知荷载和参数,然后结合传统无迹卡尔曼滤波方法对系统的非线性参数进行识别,该方法需要将系统的全部动力学响应作为观测量,条件较为苛刻。郑翥鹏等[79]基于测量误差的方差最小化原则,提出一种未知激励下的无迹卡尔曼滤波算法,能同时识别未知载荷和非线性参数。Lei等[80]提出了一种适用于未知激励的无迹卡尔曼滤波方法,可以在观测部分测点信息的情况下识别非线性结构参数,并同步估计结构未知输入力。
利用卡尔曼滤波估计状态向量时,对初始条件和噪声都不敏感。但是卡尔曼滤波算法识别结构动载荷,仅测量加速度响应容易使识别载荷受到低频噪声的干扰。EKF算法和UKF算法作为卡尔曼滤波算法的改进,可以用于非线性系统,也可以用于动载荷和结构参数的联合识别。由于需要同时进行未知载荷和未知参数的共同递归识别,EKF算法和UKF算法的稳定性要弱于KF算法,需要合理地设置滤波参数。卡尔曼滤波各算法的对比如图8所示。
贝叶斯框架中的贝叶斯正则化方法同样也被用于动载荷识别问题。贝叶斯正则化方法的主要思想是将未知激励看成随机变量,构造合适的先验分布和似然函数,令似然函数取最大值从而求出作为后验分布的载荷值。贝叶斯正则化的主要公式如下:
(18)
(19)
(20)
式中 为贝叶斯正则化初始化参数。
相关的估计流程如图9所示。
Jin等[81]利用贝叶斯正则化方法,为正则化参数的选择提供了新的思路。Jiang等[82]将贝叶斯正则化方法与Green核函数相结合以降低识别误差。此外还提出了一种新的算法来确定正则化参数的初始值,最后通过仿真和实验,表明了所提方法在处理问题的不适定性时具有明显的优势。Luo等[83]将贝叶斯正则化方法应用于分布动载荷的频域识别中,通过数值算例与Tikhonov正则化方法对比,验证了此方法的有效性。Aucejo等[84]提出了最优贝叶斯正则化方法,可以在给定可用数据的情况下确定最可能的参数,并用仿真和实验验证了该方法的有效性。严刚等[85]将冲击载荷重建问题转换为基函数系数的稀疏正则化重构问题,并用贝叶斯压缩感知方法求解该重构问题,对作用在复合材料结构上的冲击载荷时间历程进行识别,实验表明其对冲击载荷的识别具有较好的效果。Samagassi等[86]将压缩感知技术与贝叶斯正则化相结合,可以实现载荷的时域重构和定位。仿真结果表明所提出的方法优于传统的Tikhonov正则化方法。
2.5 基于数据驱动技术的动载荷识别方法
随着机器学习及人工智能的不断发展,基于数据驱动技术的动载荷识别方法逐渐建立。数据驱动动载荷幅值识别方法的基本思路是在掌握大量先验数据样本的基础上,在结构响应与动载荷之间建立映射关系,将结构动特性信息用“黑匣子”模型进行替换,进而实现不依赖结构模型而是由数据驱动的动载荷幅值识别。
在生物神经元细胞的启发下,通过建立人工神经元基本结构并组建神经网络,进而提出诸如卷积计算、门结构运算等思想,最终形成一系列人工神经网络方法,如图10所示。人工神经网络方法是近年来机器学习领域的热门问题,基于人工神经网络的深度学习动载荷幅值识别方法利用先验经验进行网络模型训练,不需要结构模型参数的参与,从而避免了动力学系统的不适定问题。早在20世纪90年代,国内外学者开始研究基于神经网络的动载荷识别方法。张方等[87]根据动力学理论推导了时域识别中神经网络的自回归函数,建立了具有时延反馈的神经网络识别模型。将网络的训练过程称为神经网络的动标定,并给出了针对各类载荷的标定方法。从神经网络载荷识别方法研究起步阶段,针对的载荷类型就不局限于集中载荷,分布动载荷、移动载荷等多种工程中常见的载荷类型也成为了神经网络载荷识别方法的研究对象。
BP神经网络因其具有自非线性映射性、适应能力强、泛化能力优越等优点被引入载荷识别问题中,并应用于海洋平台[88]、水轮发电机[89]等多种不同工程领域。但是随着BP神经网络应用范围的逐步扩大,其容易陷入局部最优化的问题也逐渐凸显。许多学者将优化方法与该神经网络结合,形成改进BP神经网络载荷识别方法以满足日益复杂的工程实际需求。王珲玮[90]针对陷入局部最优问题提出结合遗传算法优化权值的GA‑BP神经网络,对飞行器结构进行了动载荷识别,并且分析了模型的抗噪性。许扬等[91]提出了基于BP神经网络和多因素权重法的风电机组载荷预测方法。
近10年间基于神经网络的动载荷识别研究取得了较大的进展。相比前期来说,目前研究阶段的神经网络模型规模和数据规模更大、算法更加复杂[92]。如图11所示双向循环神经网络以其独特的结构建立了时间序列的前后依赖关系,并通过网络结构对数据的全序列进行遍历以提取数据特征。Yang等[93]针对简支梁结构,提出了一种基于深度双向循环神经网络的动载荷识别方法,验证了典型动载荷识别问题的可行性,考查了多点识别模型的抗噪能力,评估了超参数以及测点对识别结果的影响。
此外,Yang等[94]基于如图12所示的一维空洞卷积神经网络提出了一种动载荷识别方法,针对简支梁结构对典型动载荷进行了考查,并与传统方法进行了比较。Yang等[94]还对载荷识别中的卷积层做了一定程度的物理解释,并针对模型不确定参数问题、频域识别问题进行了研究,发现一维空洞卷积神经网络在动载荷识别问题上有较强的应用价值和实际工程意义。
为避免单一神经网络出现局部最优及泛化能力不足等问题,以多种神经网络取长补短构建新的载荷识别方法也成为了热门研究方向。廖圣瑄等 [95]将遗传算法神经网络与循环神经网络两个模型结合建立了风电机组轮毂载荷的预测模型。杨特等 [96]针对平稳随机载荷问题,利用小波变换与长短时记忆神经网络相结合的方法进行载荷识别。宋先知等 [97]基于BP神经网络和长短记忆神经网络建立了钻井过程中大钩载荷和转盘扭矩的预测模型。由于深度学习处理能力的提升,针对的载荷类型与应用的工程结构更加复杂,同时也逐渐用于处理不确定性结构[98]、非线性系统[99‑100]等的动载荷识别中。
对于基于数据驱动的动载荷识别方法来说,目前还处于研究的初级阶段。大部分研究都是基于振动数据建立动载荷识别逆模型进行可行性分析,尚未从数据特征、神经网络模型建立、解决工程难题等角度对该领域进行研究,有待进一步发展以形成完善的研究体系。此外如何降低该方法对数据规模的依赖、提升算法的可解释性、提高算法的鲁棒性也是未来潜在的发展方向。
2.6 两类不确定问题的动载荷识别方法
2.6.1 结构不确定动载荷识别方法
上文描述的动载荷识别方法都默认结构是确定的,但在实际工程中,由于制造或测量误差、材料离散性、工作环境复杂等原因,许多结构都存在不确定因素,如材料参数、几何尺寸、边界条件等。这些不确定因素会导致实际结构动力学特性与设计值之间存在偏差,此时确定性结构动载荷识别方法不再适用,否则会影响动载荷识别精度。目前,主要采用概率模型和非概率模型来处理动载荷识别中的不确定结构问题。如图13所示,概率模型需要充足的样本信息,来获得不确定性参数的概率分布特性;非概率模型仅需要不确定性参数的区间范围,适用于样本信息不足的情况。
概率模型包括蒙特卡罗模拟方法、矩阵摄动法和多项式混沌展开法。蒙特卡罗模拟方法[101]按照已知概率分布抽取随机变量的样本,对所有样本进行统计试验,将求得的统计特征值作为待求解问题的数值解,计算量非常大,不便于工程应用。矩阵摄动法将求解变量和已知变量展开为不确定性参数的幂级数形式,利用同幂项系数相等原理,将不确定性问题简化为多个确定性问题,计算量较小。孙兴盛等[102]假设杆桁架结构的横截面积、车门结构的弹性模量为不确定性参数,相互独立且服从正态分布,根据矩阵一阶摄动理论,将不确定结构动载荷识别问题转化为两类确定性逆问题,即不确定性参数均值处动载荷的识别和动载荷关于各不确定性参数的灵敏度。Wang等[56]假设机翼结构的弹性模量和泊松比为不确定性参数,相互独立且服从正态分布,基于文中提出的迭代正则化方法和矩阵一阶摄动理论对机翼不确定结构动载荷进行了识别。
矩阵摄动法虽然原理简单,但仅适用于结构不确定性水平较低的动载荷识别问题,假设动载荷识别正问题为,对于不确定结构,可以将不确定性参数表示为:
(21)
式中 为不确定性参数的均值部分;为不确定性参数的扰动部分。
根据矩阵摄动理论:
(22)
展开式(22),根据同幂项系数相等原理可得:
(23)
(24)
由于扰动部分相比均值部分较小,待识别载荷和传递函数可以近似表示为其在不确定性参数均值处的一阶泰勒展开,推导可得:
(25)
综上,不确定性问题被转化为了式(23)和式(25)描述的两类确定性问题。
多项式混沌展开法采用多项式基组合成随机空间来描述随机变量的不确定性,可以处理结构不确定性水平较高的动载荷识别问题。Wu等[103]假设随机载荷、梁结构的弹性模量和密度服从高斯分布,将不确定性参数和待识别随机载荷基于Karhunen‑Love(K‑L)展开,并分析了响应样本数量和不确定性水平对移动载荷识别结果的影响。Liu等[29]假设杆桁架结构的横截面积和密度相互独立且服从正态分布,车门和车窗的弹性模量相互独立且分别服从对数正态分布和伽玛分布,采用概率密度函数或其导数概率密度函数近似表示不确定性参数,将待识别载荷基于Gegenbauer多项式展开。Wu等[31]提出一种识别复杂不确定结构随机载荷的时域方法,假设卫星模型的弹性模量服从高斯分布,将响应和待识别载荷基于混沌多项式展开。多项式混沌展开法的适用范围较广,但需要充足的样本信息来获得不确定性参数的概率密度函数表达式。
非概率模型包括区间分析方法和凸模型理论,仅需要不确定性参数的上下界,就可以识别出载荷的上下界。Shigeru等[104]提出一种由不确定性位移响应识别线弹性体节点力的方法,根据凸模型理论将不确定性问题转化为两类确定性问题,即位移响应均值处的载荷识别和待识别载荷关于不确定性位移响应的灵敏度。王晓军等[105]假设位移响应为有界不确定性参数,将其用区间向量的形式表示,对不同位移测点识别结果求交集,以减小载荷识别结果的区间半径,提高识别精度。Liu等[106]假设杆桁架结构的弹性模量、密度和阻尼系数为不确定性参数,根据区间分析方法将不确定结构动载荷识别问题转化为两类确定性逆问题,并发现与蒙特卡罗模拟方法相比,这种方法在保证计算精度的同时,提高了计算效率。He等[30]提出一种基于非接触式声压的动载荷识别方法,假设车身结构的弹性模量和密度为不确定性参数,分别采用区间模型和椭球凸模型描述不确定性参数,发现椭球凸模型的载荷识别边界比区间模型宽。Liu等[107]假设机翼结构外蒙皮和内填料的弹性模量为不确定性参数,将其用区间向量的形式表示,基于响应叠加分解原理识别了不确定机翼结构的随机载荷边界。Wang等[36]提出基于小波变换和模态复合变换的动载荷识别方法,并将其与区间分析方法相结合,对不确定梁、板结构上的动载荷进行了识别。Cui等[108]在区间分析方法的基础上,引入卷积神经网络重构不确定结构的载荷区间,并分析了测点分布和样本数量对识别精度的影响。区间分析方法和凸模型理论适用于不确定性参数样本信息不足的情况,但它们不能处理结构不确定性水平较高的动载荷识别问题。对于不确定结构,根据区间分析理论,不确定性参数可以用区间向量的形式表示为:
(26)
式中 和分别表示不确定性参数区间向量的上界和下界。
区间向量可以改写为:
(27)
式中 表示不确定性参数区间向量的中值;表示不确定性参数区间向量的半径。
由于扰动部分相比中值较小,待识别载荷可以近似表示为其在不确定性参数区间中值处的一阶泰勒展开:
(28)
根据自然区间扩张定理,由式(28)可得:
(29)
于是,区间分析方法确定的载荷上界和下界的表达式分别为:
(30)
(31)
概率模型和非概率模型的基本思路都是将不确定性问题简化为确定性问题求解,降低了直接求解不确定结构动载荷识别问题的难度。但是,现有不确定结构动载荷识别研究局限于结构材料参数和几何尺寸的不确定性,如弹性模量、密度、阻尼、横截面积等,几乎没有对边界条件、连接关系等结构不确定性因素展开研究,并且通常假设各不确定性参数相互独立,很少考虑它们之间的相关性。
2.6.2 输入条件不确定动载荷识别方法
无论是最初的频响函数直接求逆载荷识别方法还是现如今发展迅猛的数据驱动动载荷识别方法,都离不开结构动响应作为输入,在动载荷识别过程中也会存在输入条件不确定问题。输入条件不确定问题可以分为两类:一是结构初始振动状态不确定,二是测点位置不确定。针对测点位置布置的研究目前尚在起步阶段,并未形成系统性的指导方法,因此本文不进行赘述。前面提及的动载荷识别方法,尤其是时域动载荷识别方法中都存在一个共同的假设:结构的初始振动响应为零。换句话说,也就是在进行载荷识别任务之前结构必须处于静止状态。但是在实际工程中,往往存在响应信号开始采集之前结构就已经处于振动状态的情况,例如:汽车驶入桥梁、摩天大楼受到风载以及火箭发射遥测数据采集等。同时,由于时域动载荷识别方法对于初始条件十分敏感,当初始条件不确定时,基于传统时域识别方法的动载荷识别结果会出现较大误差,如图14所示。
为解决这一问题,许多学者提出了考虑初始条件信息不足时的改良方法,以得到更准确的识别结果。例如,Pan等[109]针对未知初始条件下的外部力重建问题,提出利用冗余字典法表征未知移动荷载并采用模态空间表示未知初始条件,并引入稀疏正则化方法提升识别结果的稳定性;胡大士[110]提出一种冰载荷反演方法,能够在冰载荷作用的时间段内整体进行反求,并且不受初始条件的影响,克服了传统方法中对初始条件敏感的问题。
Jiang等[111]通过虚拟扩展响应将未知初始条件下的振动响应分解为待识别载荷引起的受迫振动和初始条件引起的自由衰减振动,并统一了动载荷受迫振动响应和初始条件引起的自由振动响应,结合Newmark‑β显式算法,构建了未知初始条件下的动载荷识别的模型,并给出了考虑未知初始条件下的动载荷识别流程,如图15所示。通过数值仿真与试验进行了验证,均取得良好识别效果。该方法不仅可以提高识别的准确性和稳定性,还进一步降低工程应用的门槛,拓宽动载荷识别技术的应用范围,促进了动载荷识别技术在实际工程中的应用。
2.7 动载荷位置识别方法
动载荷识别包含载荷位置识别和载荷幅值重构这两类问题。相对于载荷幅值重构,目前载荷位置识别问题的研究成果较少,且大部分的位置识别都是针对冲击载荷的位置识别。目前已有的动载荷位置识别方法有穷举法、三角测距法、支持向量机、人工神经网络、时间序列反演方法和参考数据库方法等。为提升求解效率,遗传算法、分离变量法等算法也被应用到位置识别中。
穷举法通过大量的测点获取载荷作用下的结构振动信息,通过激励点遍历及数值优化算法实现载荷的位置识别[112‑113]。穷举法往往需要采集大量的数据,这会导致载荷位置识别高成本的同时,数据处理上也存在一定的困难[114]。蒋祺等 [115]提出了动载荷位置识别的当量载荷误差判别法,使用不同测点在相同位置反演出的当量载荷误差,重构了单点和两点激励下平面板的动载荷位置。张景等[116]根据结构系统参数建立响应与外部载荷之间的卷积关系式,基于分离变量算法将载荷信息从脉冲响应函数矩阵中分离出来,并根据响应信息选取合适的模态,结合正则化方法解决病态问题,大大减少了矩阵求逆次数,提高了识别效率。Liu等 [117]根据最大化最小化(MM)原理提出了快速非凸重叠群稀疏性算法(FaNogSa),允许在响应测点的数量小于潜在冲击位置的数量情况下,识别冲击载荷位置并重构其时间历程。祝德春[118]提出了动载荷位置识别的最小系数判别法,由振动响应识别出系统上所有虚拟激励位置处的当量动载荷,数值上相等的两组当量动载荷所对应的虚拟激励位置即为载荷真实作用位置。如图16所示。
三角测距法是一种可以简单、有效、低成本获得载荷位置的方法,利用了冲击点、波速和冲击波到达不同测点位置的时间之间的数学关系,将动载荷位置识别问题表示为传感器和冲击波之间几何关系的非线性数学问题[119]。Zhao等 [120]提出并验证了一种集成碰撞定位方案,使用动态应变仪接收信号的到达时间,将三角定位技术与混合粒子群优化和遗传算法相结合,实现了冲击载荷的位置重构,识别精度可满足工程要求。Jang等[121]在结合三角定位技术的基础上,通过神经网络训练来提高对于信号传播距离估计的准确性。然而,三角测距法在应用于各向异性复合材料板结构时存在一定局限。由于三角测距法的应用前提是冲击波在不同传播方向上的速度已知或相同,在复合材料结构中波速随波传播方向的变化而变化,使得三角测距法难以实现低速冲击的高精度定位。此外,如何使用尽可能少的传感器以及提高识别准确率是三角测距载荷位置识别方法未来研究的方向。
支持向量机(SVM)方法的基本思想是通过非线性变换将原始样本空间变换为高维空间,从而将非线性问题转化为线性可分离问题。近年来,基于SVM的数据驱动方法已被广泛应用于定位结构所受的低速冲击。Datta等[122]从时间和应变信号中提取特征,包括峰值、平均值、标准差和能量指数,并将其选为最小二乘支持向量回归模型的输入集,以定位冲击载荷。Liu等 [123]通过基于bat算法的优化SVR模型,将时域特征、频域特征和时频域特征相结合,实现了更准确的载荷定位。虽然基于SVM的动载荷位置识别方法可以成功定位,但其对大规模训练样本难以实施,用SVM解决多分类问题存在困难。同时,SVM方法对缺失数据敏感,对参数和核函数的选择敏感。
人工神经网络方法因其具有抗干扰能力以及应用范围广被研究人员引入动载荷位置识别领域。Thiene等[124]以弯曲复合材料板为研究对象,采用神经网络重构冲击载荷并与传统的识别方法进行了对比。Wen等[125]采用快速傅里叶变换和主成分分析技术提取冲击信号的特征向量作为BP神经网络模型的输入,以相应的冲击坐标为输出,对模型进行训练,实现了碳纤维增强材料层压板的冲击载荷定位,平均误差为2.1 cm。
时间序列反演方法最早被应用于声源定位,后来被用于解决动载荷定位问题[126]。在时间序列反演方法的基础上,Park等[127]提出了一种冲击定位技术,利用时间反演、结构表面安装的压电换能器和扫描激光多普勒振动计精确定位复杂结构中的冲击载荷,并成功应用到各向同性和各向异性的结构中。Ciampa等[128]在时间序列反演方法基础上,针对复合材料结构,并结合响应信息及格林函数提出了冲击激励重构的一种图像处理方法,实现了冲击载荷空间和时间域的重构。时间序列反演方法被广泛应用于冲击载荷定位研究,但它要求足够的、高质量的响应信息以保障冲击载荷的高精度定位。
参考数据库方法通过训练网格上包含不同冲击信号信息的参考信号,将其与待识别冲击状态下采集获得的信号进行比较,并从最相似的参考信号中估计任意随机冲击载荷的作用点位置。参考数据库方法在传感器数量较少的情况下提供了更可靠的撞击定位结果。Jang等[129]基于参考数据库方法提出了一种冲击载荷定位的改进算法,减少了训练点,并且在低信噪比的信号下实现了载荷位置识别。Liu等[130]将参考数据库与随机分形搜索算法相结合,用于冲击载荷的定位。参考数据库方法需要大量时间从监测区域收集密集的训练点来建立参考数据库,这就意味着大多数当前参考数据库方法的定位准确程度很大程度上依赖于训练点的数量,并需要大量的时间成本。
针对动载荷位置识别问题,目前已经发展出多种方法并在工程中应用。但是,目前研究大多集中在已知载荷数目的位置识别,当载荷数目未知时的载荷位置识别仍是比较困难的课题。此外,现有的方法大多是针对冲击集中动载荷的定位,对于其他类型的集中动载荷或者分布动载荷,载荷位置识别需要进一步的研究。而且提高载荷位置识别效率和精度也是未来亟需解决的问题。
至此,本节对动载荷幅值识别方法和位置识别方法进行了归纳与总结,并描述了几种常用的动载荷识别过程中处理反问题不适定性的正则化方法。同时,还引出了结构不确定和输入条件不确定动载荷识别两类问题。在工程实际应用中,存在测点信息有限、工程结构复杂、工作环境恶劣等情况,可能会加剧反问题不适定性和两类不确定问题对动载荷识别精度的影响。因此,需要对这些问题展开深入研究,发展适用于复杂结构及恶劣工况的动载荷识别方法,从而拓宽动载荷识别技术的工程应用范围。
3 工程应用和局限
动载荷识别是确保工程结构设计的准确性、可行性、可靠性、安全性的基本工作,同时也是动力学分析中十分必要的环节。目前,动载荷的研究成果已广泛应用于航空航天、建筑结构、机械工程、能源系统等具有动载荷特征的工程领域,如图17所示。
在航空航天领域,需要获取飞行器在飞行过程中承受的各类动态载荷,用于实现飞行器飞行控制、健康监测等精细化管理。动载荷识别技术在该领域的部分应用如图18所示。这些外部激励力难以直接测量或者力传感器的设置会阻碍系统的运行、增加飞行器结构的负重。因此科研技术人员间接利用遥测数据或振动传感器上的响应数据,运用动载荷识别技术识别结构所受到的外载荷。例如,直升机旋翼桨叶所受载荷是直升机主要振动来源,文献 [131]利用正交多项式拟合的方法识别了直升机旋翼桨叶的分布动载荷;针对飞机的方向舵,Wang等[132]提出了一种不确定性结构的分布式动载荷识别方案;针对航天器与火箭之间的相互作用载荷难以被直接测量的问题,吴邵庆等[133]将星箭连接环上的作用载荷归类为环形分布随机动载荷进行识别;根据火箭运行过程中的遥测数据,研究人员也提出了相应的动载荷识别方法,并分别用于识别火箭整流罩[134]和固体火箭截面上的载荷[135]。
在建筑结构领域,建于地面的高层建筑[136]、核电站内的管道[137]、近海工程的海洋石油平台[138]等,它们可能承受强风、水流、地震以及波浪等各种动分布载荷的作用,动荷载及其作用下的结构响应是分析、设计建筑结构安全性和适用性的主要控制指标。动载荷识别技术在该领域的部分应用如图19所示。针对桥梁结构,车辆载荷会对桥梁安全可靠性、使用寿命产生重大影响。一些学者在对车辆载荷进行研究的过程中,也促进了移动载荷识别方法的不断发展[139]。如潘楚东[140]借助稀疏正化和移动平均的思想,实现对桥梁的移动载荷和结构损伤的同时识别;田瑞欣[141]通过BP 神经网络进行桥梁移动荷载相关参数的识别,为桥梁的全寿命周期运营管理提供数据支持;Fitzgerald 等[142]通过优化Tikhonov正则化参数的选取方式,准确识别桥梁上所承受的车辆动态轴重。
在机械工程领域,动载荷识别有助于评估机械零件的耐久性和受力情况,从而指导设计和改进工艺。部分应用如图20所示。对于工程机械,大多数工作环境都比较恶劣,结构承受的动载荷情况十分复杂。针对矿山机械结构,Wang等[144]引入优化算法来确定矿山机械运行过程中的实际工程动载荷。在岩石掘进机的使用中[145],准确获取结构所承受的载荷是掘进机自动调节截割参数的基础,为掘进机作业安全性和截割效率的提高提供可靠的依据。履带行驶系统长期工作在恶劣的环境中,张志宏等[146]提出了针对履带行驶系统中链板间拉力的动载荷识别方法,为履带系统的结构优化设计和耐久性分析提供了参考。Liu等[147]对机械工程领域内的动载荷识别技术进行了系统介绍,为实际复杂结构的动载荷识别提供了指导,并为进一步的研究提供了可能。
在能源系统领域,大力开发和利用可再生能源已经成为必然趋势。随着风能和水势能等绿色能源的迅速开发,全球范围内的风电和水电装机容量在不断增长,行业面临的动力学和承载问题也不断凸显。该领域所面临的部分动力学问题如图21所示。为开发更具竞争力和高可靠性的发电机组,必须掌握这些发电机组所承受的各项载荷,可以为后续机组的轻量化和可靠性设计提供支撑。巫发明[148]将动态载荷识别技术应用于风电机组传动链和塔筒的受载分析,将机组的受载情况作为基本运行数据,提供给机组进行监控和部件健康诊断分析;针对风机转子系统,毛文贵等[149]提出了改进的信赖域模型管理技术近似优化算法来识别其中的不对中载荷,作为风力发电系统故障诊断的评判依据之一;针对水轮发电机组竖向振动问题,宋志强等[150]提出了基于正交多项式分解的水力机组动荷载时域识别方法,为机墩竖向动荷载的确定提供了有效途径。
除了上述应用领域外,动载荷识别方法在其他方面也得到了应用,如临时看台动载荷识别[151]、路面谱识别[152]、桅杆结构动载荷识别[153]、支撑平台动载荷识别[154]等。
然而动载荷识别技术发展到今天,受到了系统模型建立、信号测试预处理、载荷特性、噪声特性等多方面因素的影响。当前的动载荷识别技术仍然存在以下局限和不足:
(1)结构的高复杂度对载荷识别在工程上的应用带了极大的挑战。识别结构动载荷之前,往往需要对结构模型进行简化,难免引起一定的模型误差。准确的模型参数是进行载荷识别的基础,但实际工程中,模型参数并不容易确定。比如阻尼参数数值小且难以确定,环境中的温度、湿度都会对阻尼产生影响,从而影响载荷识别的精度。另外,在实际工程应用中存在一定的非线性因素,比如大挠度梁、非线性接触等非线性因素会加大系统建模的难度,载荷识别结果的可靠性也难以保障。
(2)有限的测量信息及噪声扰动也阻碍了动载荷识别技术在工程应用中的快速发展。在实际工程结构中,传感器的类型选择和布置受到了具体应用场景的限制,能测定的动响应信息往往是受限的、有限的,特定的响应类型、有限的测点布置对动载荷识别方法提出了苛刻的要求。另外,响应信号测试会受到噪声干扰,测量的高噪声水平必将严重阻碍动载荷识别的应用。目前各类动载荷识别方法对于测量噪声一般考虑为高斯白噪声,但实际情况下响应中的噪声并不一定是高斯白噪声,例如遥测数据中背景噪声的非高斯特性比较明显,在此假设下,动载荷识别方法将不能准确地识别结构上的未知载荷。此外,在实际测量过程中,动响应有时并不是从零初始条件开始测试,对于低阻尼结构而言,初始条件的估计错误也会使载荷识别的时域结果产生偏差。
(3)动载荷模型难以精确表征制约了动载荷识别的工程应用。工程结构会受到多种载荷的耦合作用,如飞机机翼会同时受到发动机激励、舵面激励以及分布气动力激励的共同作用,载荷类型复杂,载荷作用空间也未知。工程结构如位于高温、高压和强电磁场等环境中,这些苛刻的工作环境也很难用恰当的载荷模型进行模拟。如何精确地构建符合实际情况的载荷模型是一项十分具有挑战性的工作。
(4)动载荷识别作为动力学的逆问题,耦合复杂高维度系统,往往存在着严重的病态问题。工程结构模型复杂度、载荷维数过大、或测点选择不恰当、识别算法类型等因素都可能加剧问题的病态性。目前流行的正则化方法仅仅是改善载荷识别问题的病态性,理想的做法是避免所构建的动载荷识别模型病态。
上述动载荷识别在工程实际应用中的局限,严重影响了动载荷识别技术进一步推广,动载荷识别方法目前还存在极大的发展空间。由于在设计阶段无法给出合适的动载荷,众多装备在研制过程中还是采用“静力学设计,动力学校核”的策略,这种策略可能会出现反复迭代的设计循环,增加了时间和经济上的成本。若能事先准确获取外部激励信息,为结构动力学设计、优化提供输入依据,必能缩短研发周期,提高动力学设计的效率。预期未来随着产品设计愈来愈趋于精细化,测量仪器的精度不断提高,以及算法理论的不断创新,动载荷识别也必然会在各个领域得到更广泛的应用。
4 总结与展望
本文对动载荷识别基本原理、发展历程、研究成果以及存在的关键问题进行了归纳和讨论。动载荷识别技术发展至今,得益于动力学精细化建模、测试传感、机器学习和大数据等技术的不断发展;动载荷识别技术已经被应用于航空航天、建筑结构、机械工程、能源系统等领域。但是,仍然存在很多瓶颈限制了动载荷识别技术的工程应用,本文对目前动载荷识别的工程应用进行了总结,并分析了应用中的局限性。
未来结构动载荷识别要侧重基础理论研究和工程应用研究,两者相辅相成,相互促进。在基础理论研究中,突破动载荷识别的核心科学问题,发展精准化、高效化、智能化、实时化的动载荷识别方法;在工程应用中实现动载荷识别的在线化、系统化、普适化、规范化,提升动载荷识别技术的成熟度。动载荷识别技术的发展必将促进重大装备等工程结构的动力学设计、优化、控制等能力的大幅提升。具体而言,未来动载荷识别技术或将朝以下发展方向展开:
(1)面向动载荷识别高精度的需求,未来还需对动载荷识别的不适定问题、不确定问题进行持续研究,突破初始条件未知等信息不足的动载荷识别难题,进一步提高载荷识别的稳定性和识别精度;
(2)动载荷识别与人工智能(AI)技术的结合。目前以数据驱动为主要手段的人工智能方法发展迅速,在模式辨识等方向具有独特的优势。将人工智能与动载荷识别相结合,发展基于小样本数据的、可解释性强、鲁棒性强的动载荷人工智能算法,研究基于数字孪生的深度学习策略,也将成为未来的发展方向;
(3)发展适用于非线性结构、时变结构、不确定性结构的动载荷识别方法,进一步提升动载荷识别的适用范围;
(4)针对载荷类型多样、特性不一、作用形式复杂的载荷识别问题,发展多源混合载荷及基础激励载荷的重构方法,同步准确辨识出不同形式载荷源,厘清各形式载荷对响应的贡献;
(5)针对航空飞行器、直升机旋翼等复杂结构系统气动载荷源辨识的难题,建立适用于航空航天结构连续分布气动载荷的反演方法,实现航空航天结构动载荷环境的准确预示;
(6)面向无人驾驶汽车、智能飞行器、机器人等智能系统智能感知的需求,开展动力学环境的反演方法研究,实现动力学环境的在线化、高效化、智能化预示,对于促进智能设备的发展意义重大;
(7)动载荷识别技术也离不开先进的测量技术,将来采取分布式或更先进的测量技术,实施多源信息融合,获取高精度的、足够多的响应信息,为动载荷识别提供可靠的输入信息;
(8)发展高效率的动载荷位置识别方法,大幅度提升动载荷位置识别效率;开展动载荷位置和个数辨识以及分布动载荷位置定位方法研究,拓展位置识别的内涵;进一步发展动载荷位置和幅值的同步识别;
(9)将动载荷识别技术与结构健康监测相结合,开展在线动载荷识别及结构健康监测研究,及时高效地重构激励动载荷并评估结构健康状态,为工程结构的维护提供科学可靠依据,提高结构的安全性与可靠性;
(10)针对不断涌现的诸如高温、高速等极端苛刻环境,热场、磁场、电场等多场耦合环境,新材料、新布局形式等复杂结构模型,开展高精度、高效率动载荷识别研究;
(11)开发可应用于工程实践的动载荷识别软硬件平台系统,结合云计算等优势,促使动载荷识别方法的网络化,提升动载荷识别技术的成熟度,解决重大装备面临的动力学技术瓶颈。
参考文献:
[1]许锋,陈怀海,鲍明.机械振动载荷识别研究的现状与未来[J].中国机械工程,2002,13(6):526‑531.
XU Feng,CHEN Huaihai,BAO Ming. Force identification for mechanical vibration: state-of-the‑art and prospect[J]. China Mechanical Engineering,2002,13(6):526‑531.
[2]Bartlett F D,Flannelly W D. Modal verification of force determination for measuring vibratory loads[J]. Journal of the American Helicopter Society,1979,24:10‑18.
[3]Desanghere G,Snoeys R. Indirect identification of excitation forces by modal coordinate transformation[C]// 3rd International Modal Analysis Conference. Orlando,USA,1985: 685‑690.
[4]Wang L,Liu Y R,Xu H Y. Recent developments in dynamic load identification for aerospace vehicles considering multi‑source uncertainties[J]. Transactions of Nanjing University of Aeronautics & Astronautics,2021,38(2): 271‑287.
[5]Giansamte N,Jones R,Calapodas N J. Determination of in‑flight helicopter loads[J]. Journal of the American Helicopter Society,1982,27(3):58‑64.
[6]Starkey J M,Merrill G L. On the ill‑condition nature of indirect force‑measurement techniques[J]. International Journal of Analysis and Experimental Modal Analysis,1989,4(3):103‑108.
[7]Karlsson S E S. Identification of external structural loads from measured harmonic responses[J]. Journal of Sound and Vibration,1996,196(1):59‑74.
[8]Lin J H,Guo X L,Zhi H,et al. Computer simulation of structural random loading identification[J]. Computers & Structures,2001,79(4):375‑387.
[9]姜金辉,陈国平,张方.多点平稳随机载荷识别方法研究[J].振动工程学报,2009,22(2):162‑167.
JIANG Jinhui,CHEN Guoping,ZHANG Fang. Identification method of multi‑point stationary random load[J]. Journal of Vibration Engineering,2009,22(2):162‑167.
[10]Jia Y,Yang Z C,Guo N,et al. Random dynamic load identification based on error analysis and weighted total least squares method[J]. Journal of Sound and Vibration,2015,358:111‑123.
[11]Hollandsworth P E,Busby H R. Impact force identification using the general inverse technique[J]. International Journal of Impact Engineering,1989,8(4): 315‑322.
[12]赵凤遥,张运良,马震岳. 动载荷的时域识别方法及其应用[J]. 水电能源科学,2005(1): 8‑11.
ZHAO Fengyao,ZHANG Yunliang,MA Zhenyue. Method and application of dynamic load identification in time domain[J]. Water Resources and Power,2005(1): 8‑11.
[13]胡杰,范宣华.一种时域载荷识别数值算法及其不适定性研究[J]. 应用力学学报,2017,34(2): 324‑328.
HU Jie,FAN Xuanhua. Ill‑posedness research of a load identification method in time domain[J]. Chinese Journal of Applied Mechanics,2017,34(2): 324‑328.
[14]文祥荣,智浩,孙守光. 结构动态载荷识别的精细逐步积分法[J]. 工程力学,2001,18(4): 117‑122.
WEN Xiangrong,ZHI Hao,SUN Shouguang. Highly precise direct integration scheme for structural dynamic load identification[J]. Engineering Mechanics,2001,18(4): 117‑122.
[15]王静,陈海波,王靖. 基于精细积分的冲击载荷时域识别方法研究[J]. 振动与冲击,2013,32(20): 81‑85.
WANG Jing,CHEN Haibo,WANG Jing. Impulsive load identification in time domain based on precise time‑integration method[J]. Journal of Vibration and Shock,2013,32(20): 81‑85.
[16]王淑娟,韩伟民,王国巧,等. 基于二阶系统解耦的精细积分格式下动载荷时域识别[J]. 计算力学学报,2017,34(5): 631‑637.
WANG Shujuan,HAN Weimin,WANG Guoqiao,et al. Dynamic load identification using second‑order formulation in time domain based precise time‑integration[J]. Chinese Journal of Computational Mechanics,2017,34(5): 631‑637.
[17]姜金辉,徐菁,张方,等. Wilson‑θ反分析法的动载荷识别精度的若干问题[J].振动、测试与诊断,2013,33(5):782‑788.
JIANG Jinhui,XU Jing,ZHANG Fang,et al. Accuracy of the load identification based on inverse analysis of Wilson‑θ method[J]. Journal of Vibration,Measurement & Diagnosis,2013,33(5):782‑788.
[18]Kortis J,Daniel L. Application of the Newmark numerical method with contact algorithm to the solution of the vehicle‑bridge interaction[J]. Procedia Engineering,2016,153:298‑303.
[19]Liu K,Law S S,Zhu X Q,et al. Explicit form of an implicit method for inverse force identification[J]. Journal of Sound and Vibration,2014,333(3):730‑744.
[20]Jiang Jinhui,Ding Ming,Li Jun. A novel time‑domain dynamic load identification numerical algorithm for continuous systems[J]. Mechanical Systems and Signal Processing,2021,160: 107881.
[21]Mohammadzadeh S,Ghassemieh M,Park Y. Structure-dependent improved Wilson‑θ method with higher order of accuracy and controllable amplitude decay[J]. Applied Mathematical Modelling,2017,52: 417‑436.
[22]陈英华. 动载荷时域Wilson‑θ识别方法和PATRAN二次开发 [D]. 南京:南京航空航天大学,2010.
CHEN Yinghua. Dynamic load identification Wilson‑θ method in time domain and PATRAN secondary development[D]. Nanjing: Nanjing University of Aeronautics and Astronautics,2010.
[23]徐菁,张方,姜金辉,等.运用数值迭代的动载荷识别算法[J].振动工程学报,2014,27(5): 702‑707.
XU Jing,ZHANG Fang,JIANG Jinhui,et al. An algorithm of dynamic load identification based on numerical iteration[J]. Journal of Vibration Engineering,2014,27(5): 702‑707.
[24]徐菁,张方,姜金辉,等.基于拟静态初值的载荷识别数值修正算法[J].振动与冲击,2016,35(2): 39‑44.
XU Jing,ZHANG Fang,JIANG Jinhui,et al. Numerical correcting algorithm for load identification based on quasi‑static initial value[J]. Journal of Vibration and Shock,2016,35(2): 39‑44.
[25]Wu E,Tsai T D,Yen C S. Two methods for determining impact‑force history on elastic plates[J]. Experimental Mechanics,1995,35(1):11‑18.
[26]韩旭,刘杰,李伟杰,等.时域内多源动态载荷的一种计算反求技术[J].力学学报,2009,41(4):595‑602.
HAN Xu,LIU Jie,LI Weijie,et al. A computational inverse technique for reconstruction of multisource loads in time domain[J]. Chinese Journal of Theoretical and Applied Mechanics,2009,41(4):595‑602.
[27]缪炳荣,周凤,陈翔宇,等. 利用核函数和不同正则化方法的结构载荷识别混合技术研究[J].振动工程学报,2018,31(4):553‑560.
MIAO Bingrong,ZHOU Feng,CHEN Xiangyu,et al. Research of the structure load identification hybrid technology using kernel function and different regularization method[J]. Journal of Vibration Engineering,2018,31(4):553‑560.
[28]孔帅,崔洪宇,季顺迎.船体结构冰载荷反演方法及试验验证[J].中国机械工程,2020,31(3):281‑288.
KONG Shuai,CUI Hongyu,JI Shunying. Ice load identification method of ship structures and experimental verification[J]. China Mechanical Engineering,2020,31(3):281‑288.
[29]Liu J,Sun X S,Han X. Dynamic load identification for stochastic structures based on Gegenbauer polynomial approximation and regularization method[J]. Mechanical Systems and Signal Processing,2015,56‑57:35‑54.
[30]He Z C,Lin X Y,Li E,A non‑contact acoustic pressure-based method for load identification in acoustic-structural interaction system with non‑probabilistic uncertainty[J]. Applied Acoustics,2019,148:223‑237.
[31]Wu S Q,Zheng Y,Sun Y W,et al. Identify the stochastic dynamic load on a complex uncertain structural system[J]. Mechanical Systems and Signal Processing,2021,147:107114.
[32]Liu Huanlin,Yu Ling,Luo Ziwei,et al. Compressed sensing for moving force identification using redundant dictionaries[J]. Mechanical Systems and Signal Processing,2020,138:106535.
[33]Pan Chudong,Yu Ling,Liu Huanlin,et al. Moving force identification based on redundant concatenated dictionary and weighted L1‑norm regularization[J]. Mechanical Systems and Signal Processing,2018,98:32‑49.
[34]何文博,许步锋,冯振宇,等.利用冗余扩展余弦字典的复杂动载荷识别研究[J].振动工程学报,2024,37(3):512‑521.
HE Wenbo,XU Bufeng,FENG Zhenyu,et al. Identification of complex dynamic load using redundant extended cosine transform dictionary[J]. Journal of Vibration Engineering,2024,37(3):512‑521.
[35]池林,刘杰,姜潮.时域内动态载荷识别的径向基形函数法[J].中国机械工程,2013,24(3):285‑289.
CHI Lin,LIU Jie,JIANG Chao. Radial basis shape function method for identification of dynamic load in time domain[J]. China Mechanical Engineering,2013,24(3):285‑289.
[36]Wang Lei,Xu Hanying,Liu Yaru,et al. A novel dynamic load identification approach for multi‑source uncertain structures based on the set‑theoretical wavelet transform and layered noise reduction[J]. Structures,2023,51:91‑104.
[37]Li Zong,Feng Zhipeng,Chu Fulei,et al. A load identification method based on wavelet multi‑resolution analysis[J]. Journal of Sound and Vibration,2014,333(2):381‑391.
[38]Lu C,Zhu L C,Liu J,et al. The least squares time element method based on wavelet approximation for structural dynamic load identification[J]. International Journal of Computational Methods,2023,20(9): 2350008.
[39]Granger S,Perotin L. An inverse method for the identification of a distribution random excitation acting on a vibrating structure part 1: theory[J]. Mechanical Systems and Signal Processing,1999,13(1): 53‑65.
[40]张方,朱德懋. 动态载荷时域识别的级数方法[J]. 振动工程学报,1996,9(1):1‑8.
ZHANG Fang,ZHU Demao. Identification of dynamic load based on series expansion[J]. Journal of Vibration Engineering,1996,9(1):1‑8.
[41]张方,秦远田,邓吉宏.复杂分布动载荷识别技术研究[J]. 振动工程学报 ,2006,19(1):81‑85.
ZHANG Fang,QIN Yuantian,DENG Jihong. Research of identification technology of dynamic load distributed on the structure[J]. Journal of Vibration Engineering,2006,19(1):81‑85.
[42]姜金辉. 分布随机动载荷识别理论与方法[D]. 南京:南京航空航天大学,2010.
JIANG Jinhui. Reconstruction of distributed random dynamic loads‑theory and methodology[D]. Nanjing: Nanjing University of Aeronautics and Astronautics,2010.
[43]Li K,Liu J,Han X,et al. A novel approach for distributed dynamic load reconstruction by space-time domain decoupling[J]. Journal of Sound and Vibration,2015,348: 137‑148.
[44]Wang Lei,Liu Yaru,Liu Yisi. An inverse method for distributed dynamic load identification of structures with interval uncertainties[J]. Advances in Engineering Software,2019,131 :77‑89.
[45]Jiang Jinhui,Kong Huangfei,Yang Hongli,et al. One identification method of distributed dynamic load based on modal coordinate transformation for thin plate structure[J]. International Journal of Computational Methods,2021,18(7): 1‑18.
[46]姜昊. 非接触分布激励下的动态标定技术[D].南京:南京航空航天大学,2008.
Jiang Hao. The technology of the dynamic calibration under non‑contact distributed excitation[D]. Nanjing: Nanjing University of Aeronautics and Astronautics,2008.
[47]Jiang J H,Luo S Y,Zhang F. One novel dynamical calibration method to identify two‑dimensional distributed load[J]. Journal of Sound and Vibration,2021,515: 116465.
[48]杨帆,张方.基于小波级数分解法的动载荷识别研究[J].清华大学学报(自然科学版),2013,53(8):1166‑1171.
YANG Fan,ZHANG Fang. Identification of dynamic force based on wavelet series decomposition[J]. Journal of Tsinghua University(Science and Technology),2013,53(8):1166‑1171.
[49]Berry A,Robin O,Pierron F. Identification of dynamic loading on a bending plate using the virtual fields method[J]. Journal of Sound and Vibration,2014,333(26):7151‑7164.
[50]Li Xiaowang,Zhao Haitao,Chen Zheng,et al. Identification of distributed dynamic excitation based on Taylor polynomial iteration and cubic Catmull‑Rom spline interpolation[J]. Inverse Problems in Science and Engineering,2020,28(2):220‑237.
[51]Liu J,Li K. Sparse identification of time‑space coupled distributed dynamic load[J]. Mechanical Systems and Signal Processing,2021,148: 107177.
[52]Zheng Y,Wu S Q,Fei Q G. Distributed dynamic load identification on irregular planar structures using subregion interpolation[J]. Journal of Aircraft,2021,58(2): 288‑299.
[53]梅立泉,崔维庚.面载荷识别的TSVD正则化方法[J].应用力学学报,2010,27(1):140‑144.
MEI Liquan,CUI Weigeng. TSVD regularization method for area load reconstruction[J]. Chinese Journal of Applied Mechanics,2010,27(1): 140‑144.
[54]Zhen Chen,Chan T H T. A truncated generalized singular value decomposition algorithm for moving force identification with ill‑posed problems[J]. Journal of Sound and Vibration,2017,401: 297‑310.
[55]Fan Yuchuan,Zhao Chunyu,Yu Hongye,Research on dynamic load identification based on explicit Wilson‑θ and improved regularization algorithm[J]. Shock and Vibration,2019,2019: 8756546.
[56]Wang L J,Peng Y L,Xie Y X,et al. A new iteration regularization method for dynamic load identification of stochastic structures[J]. Mechanical Systems and Signal Processing,2021,156:107586.
[57]陈辉,缪炳荣,赵浪涛,等. 基于L1范数正则化和最小二乘优化的冲击载荷识别研究[J].噪声与振动控制,2023,43(1):62‑67.
CHEN Hui,MIAO Bingrong,ZHAO Langtao,et al. Research on impact load identification based on L1‑norm regularization and least squares optimization[J]. Noise and Vibration Control,2023,43(1):62‑67.
[58]Qiao B J,Zhang X W,Wang C X,et al. Sparse regularization for force identification using dictionaries[J]. Journal of Sound & Vibration,2016,368:71‑86.
[59]Choi H G,Thite A N,Thompson D J. Comparison of methods for parameter selection in Tikhonov regularization with application to inverse force determination[J]. Journal of Sound and Vibration,2007,304(3‑5): 894‑917.
[60]Kalman R E. A new approach to linear filtering and prediction problems[J]. Journal of Fluids Engineering,1960,82 (1):35‑45.
[61]Steven Gillijns,Bart De Moor. Unbiased minimum-variance input and state estimation for linear discrete‑time systems with direct feedthrough[J]. Automatica,2007,43(5): 934‑937
[62]Lourens E,Reynders E,De Roeck G,et al. An augmented Kalman filter for force identification in structural dynamics[J]. Mechanical Systems and Signal Processing,2012,27:446‑460.
[63]Jiang Jinhui,Luo Shuyi,Mohamed M Shadi,et al. Real‑time identification of dynamic loads using inverse solution and Kalman filter[J]. Applied Sciences,2020,10(19): 6767.
[64]杨智春,贾有.动载荷识别方法的研究进展[J].力学学报,2015,47(2):384.
YANG Zhichun,JIA You. Advance of studies on the identification of dynamic load[J]. Chinese Journal of Theoretical and Applied Mechanics,2015,47(2):384.
[65]Saeed Eftekhar Azam,Eleni Chatzi,Costas Papadimitriou. A dual Kalman filter approach for state estimation via output‑only acceleration measurements[J]. Mechanical Systems and Signal Processing,2015,60: 866‑886.
[66]梁忠仔. 动载荷在线识别方法研究[D]. 南京:南京航空航天大学,2018.
LIANG Zhongzi. Research on the method of online identification of dynamic load[D]. Nanjing:Nanjing University of Aeronautics and Astronautics,2018.
[67]Ma C K,Ho C C. An inverse method for the estimation of input forces acting on non‑linear structural systems[J]. Journal of Sound and Vibration,2004,275: 953‑971.
[68]谢丽宇,李宪之,张睿,等. 基于自适应扩展卡尔曼滤波的消能减震结构及附加阻尼力识别[J]. 湖南大学学报(自然科学版),2020,47(11): 66‑73.
XIE Liyu,LI Xianzhi,ZHANG Rui,et al. Identification of a passively‑controlled energy dissipation structure and additional damping force based on adaptive extended Kalman filter[J]. Journal of Hunan University (Natural Sciences),2020,47(11):66‑73.
[69]张肖雄,贺佳. 基于扩展卡尔曼滤波的结构参数和荷载识别研究 [J]. 工程力学,2019,36(4):221‑230.
ZHANG Xiaoxiong,HE Jia. Identification of structural parameters and unknown excitations based on the extended Kalman filter[J]. Engineering Mechanics,2019,36(4):221‑230.
[70]Guo L,Ding Y,Wang Z,et al. A dynamic load estimation method for nonlinear structures with unscented Kalman filter[J]. Mechanical Systems and Signal Processing,2018,101:254‑273
[71]王婷,万志敏.基于无迹变换的结构载荷/参数联合识别的GDF法[J].振动与冲击,2022,41(9):75‑80.
WANG Ting,WAN Zhimin. GDF‑UT algorithm for joint identification of structural loads/parameters[J]. Journal of Vibration and Shock,2022,41(9):75‑80.
[72]Yang J N,Pan S,Huang H. An adaptive extended Kalman filter for structural damage identifications Ⅱ: unknown inputs[J]. Structural Control and Health Monitoring,2007,14(3): 497‑521.
[73]Lei Y,Jiang Y Q,Xu Z Q. Structural damage detection with limited input and output measurement signals[J]. Mechanical Systems and Signal Processing,2012,28: 229‑243.
[74]Naets F,Croes J,Desmet W. An online coupled state/input/parameter estimation approach for structural dynamics[J]. Computer Methods in Applied Mechanics & Engineering,2015,283:1167‑1188.
[75]黄丽媛. 基于滤波技术的桥梁结构参数识别研究[D]. 南京:东南大学,2019.
HUANG Liyuan.Research on parameter identification of bridge structure based on filter technique[D]. Nanjing: Southeast University,2019.
[76]Ding Y,Zhao B Y,Wu B,et al. Simultaneous identification of structural parameter and external excitation with an improved unscented Kalman filter[J]. Advances in Structural Engineering,2015,18(11):1981‑1998.
[77]Al‑Hussein A,Haldar A. Novel unscented Kalman filter for health assessment of structural systems with unknown input[J]. Journal of Engineering Mechanics,2015,141(7): 0401501.
[78]Al‑Hussein A,Haldar A. Unscented Kalman filter with unknown input and weighted global iteration for health assessment of large structural systems[J]. Structural Control and Health Monitoring,2016,23(1): 156‑175.
[79]郑翥鹏,邱昊,夏丹丹,等.未知激励下的无迹卡尔曼滤波新方法[J].工程力学,2019,36(6):29‑35.
ZHENG Zhupeng,QIU Hao,XIA Dandan,et al. A novel unscented Kalman filter with unknown input[J]. Engineering Mechanics,2019,36(6):29‑35.
[80]Lei Y,Xia D D,Erazo K,et al. A novel unscented Kalman filter for recursive state‑input‑system identification of nonlinear systems[J]. Mechanical Systems and Signal Processing,2019,127: 120‑135.
[81]Jin B T,Zou J. Augmented Tikhonov regularization[J]. Inverse Problems,2009,25(2): 025001.
[82]Jiang J H,Tang H Z,Mohamed M S,et al. Augmented Tikhonov regularization method for dynamic load identification[J]. Applied Sciences,2020,10(18): 6348.
[83]Luo S Y,Jiang J H,Zhang F,et al. Distributed dynamic load identification of beam structures using a Bayesian method[J]. Applied Sciences,2023,13(4):2537.
[84]Aucejo M,De Smet O. An optimal Bayesian regularization for force reconstruction problems[J]. Mechanical Systems and Signal Processing,2019,126: 98‑115.
[85]严刚,孙浩.基于贝叶斯压缩感知的复合材料结构冲击载荷识别研究[J].振动工程学报,2018,31(3):483‑489.
YAN Gang,SUN Hao. Identification of impact for composite structure using Bayesian compressive sensing[J]. Journal of Vibration Engineering,2018,31(3):483‑489.
[86]Samagassi S,Jacquelin E,Khamlichi A,et al. Bayesian sparse regularization for multiple force identification and location in time domain[J]. Inverse Problems in Science and Engineering,2019,27(9):1221‑1262.
[87]张方,朱德懋. 基于神经网络模型的动载荷识别[J]. 振动工程学报,1997,10(2): 156‑162.
ZHANG Fang,ZHU Demao. The dynamic load identification research based on neural network model[J]. Journal of Vibration Engineering,1997,10(2): 156‑162.
[88]林近山,窦春红,马汝建. 基于神经网络的海洋平台振动载荷识别[J]. 石油机械,2007,35(9): 95‑97.
LIN Jinshan,DOU Chunhong,MA Rujian. Vibration load identification of offshore platform based on neural network[J]. China Petroleum Machinery,2007,35(9): 95‑97.
[89]沙瑞华,张运良,李冬阳. 改进BP网络用于水轮发电机组动载识别的探讨[J]. 东北水利水电,2005,23(2): 8‑10.
SHA Ruihua,ZHANG Yunliang,LI Dongyang. Discussion on hydrogenerator dynamic load distinguished by improved BP network[J]. Water Resources & Hydropower of Northeast China,2005,23(2): 8‑10.
[90]王珲玮. 基于神经网络的飞行器力载荷识别算法研究[D]. 杭州: 浙江大学,2018.
WANG Hunwei. Research on load identification algorithm of aircraft based on neural network[D]. Hangzhou: Zhejiang University,2018.
[91]许扬,蔡安民,张林伟,等. 基于BP神经网络和多因素权重法的风电机组载荷预测和分析[J]. 热力发电,2022,51(8): 42‑49.
XU Yang,CAI Anmin,ZHANG Linwei,et al. Load prediction and analysis of wind turbine based on BP neural network and multi‑factor weight method[J]. Thermal Power Generation,2022,51(8): 42‑49.
[92]夏鹏,杨特,徐江,等. 利用时延神经网络的动载荷倒序识别[J]. 航空学报,2021,42(7): 382‑390.
XIA Peng,YANG Te,XU Jiang,et al. Reversed time sequence dynamic load identification method using time delay neural network[J]. Acta Aeronautica et Astronautica Sinica,2021,42(7): 382‑390.
[93]Yang H J,Jiang J H,Chen G P,et al. A recurrent neural network‑based method for dynamic load identification of beam structures[J]. Materials,2021,14(24): 7846.
[94]Yang H J,Jiang J H,Chen G P,et al. Dynamic load identification based on deep convolution neural network[J]. Mechanical Systems and Signal Processing,2023,185: 109757.
[95]廖圣瑄,马晓明,韩中合,等. 基于组合模型的风电机组轮毂载荷预测方法研究[J]. 中国测试,2021,47(5): 39‑45.
LIAO Shengxuan,MA Xiaoming,HAN Zhonghe,et al. Research on prediction method of wheel hub load of wind turbine based on combined model[J]. China Measurement & Test,2021,47(5): 39‑45.
[96]杨特,杨智春,梁舒雅,等. 平稳随机载荷的信号特征提取与深度神经网络识别[J]. 航空学报,2022,43(9): 402‑410.
YANG Te,YANG Zhichun,LIANG Shuya,et al. Feature extraction and identification of stationary random dynamic load using deep neural network[J]. Acta Aeronautica et Astronautica Sinica,2022,43(9): 402‑410.
[97]宋先知,朱硕,李根生,等. 基于BP‑LSTM双输入网络的大钩载荷与转盘扭矩预测[J]. 中国石油大学学报(自然科学版),2022,46(2): 76‑84.
SONG Xianzhi,ZHU Shu,LI Gensheng,et al.Prediction of hook load and rotary drive torque during well-jCpmFMvp687t3wmeDBNdlMSK2Q61aFlrKlPY+Zl9NY0=drilling using a BP‑LSTM network[J]. Journal of China University of Petroleum(Edition of Natural Science) ,2022,46(2): 76‑84.
[98]Wang L,Liu Y R,Gu K X,et al. A radial basis function artificial neural network (RBF ANN) based method for uncertain distributed force reconstruction considering signal noises and material dispersion[J]. Computer Methods in Applied Mechanics and Engineering,2020,364: 112954.
[99]Zhou J M,Dong L L,Guan W,et al. Impact load identification of nonlinear structures using deep Recurrent Neural Network[J]. Mechanical Systems and Signal Processing,2019,133: 106292.
[100]Ghajari M,Sharif‑Khodaei Z,Aliabadi M H,et al. Identification of impact force for smart composite stiffened panels[J]. Smart Materials and Structures,2013,22(8):085014.
[101]Schuëller G I. A state‑of‑the‑art report on computational stochastic mechanics[J]. Probabilistic Engineering Mechanics,1997,12(4):197‑321.
[102]孙兴盛,刘杰,丁飞,等.基于矩阵摄动的随机结构动态载荷识别技术[J].机械工程学报,2014,50(13):148‑156.
SUN Xingsheng,LIU Jie,DING Fei,et al. Identification method of dynamic loads for stochastic structures based on matrix perturbation theory[J]. Journal of Mechanical Engineering,2014,50(13):148‑156.
[103]Wu S Q,Law S S. Moving force identification based on stochastic finite element model[J]. Engineering Structures,2010,32(4):1016‑1027.
[104]Shigeru Nakagiri,Keiko Suzuki. Finite element interval analysis of external loads identified by displacement input with uncertainty[J]. Computer Methods in Applied Mechanics and Engineering,1999,168(1‑4):63‑72.
[105]王晓军,杨海峰,邱志平,等.基于Green函数的动态载荷区间识别方法研究[J].固体力学学报,2011,32(1):95‑101.
WANG Xiaojun,YANG Haifeng,QIU Zhiping,et al. Research on interval identification method for dynamic loads based on Green’s function[J]. Chinese Journal of Solid Mechanics,2011,32(1):95‑101.
[106]Liu J,Sun X S,Meng X H,et al. A novel shape function approach of dynamic load identification for the structures with interval uncertainty[J]. International Journal of Mechanics and Materials in Design,2016,12(3):375‑386.
[107]Liu Yaru,Wang Lei. A two‑step weighting regularization method for stochastic excitation identification under multi‑source uncertainties based on response superposition-decomposition principle[J]. Mechanical Systems and Signal Processing,2023,182:109565.
[108]Cui W X,Jiang J H,Sun H Y,et al. Data‑driven load identification method of structures with uncertain parameters[J]. Acta Mechanica Sinica,2024,40(2): 523138.
[109]Pan C D,Yu L. Identification of external forces via truncated response sparse decomposition under unknown initial conditions[J]. Advances in Structural Engineering,2019,22(15): 3161‑3175.
[110]胡大士. 基于正则化方法的动载荷识别技术研究[D]. 大连:大连理工大学,2020.
HU Dashi. Research on dynamic load identification technology based on regularization method[D]. Dalian: Dalian University of Technology,2020.
[111]Jiang J H,Cui W X,Chen S,et al. A novel dynamic load identification method based on improved basis functions and implicit Newmark‑β for continuous system with unknown initial conditions[J]. Mechanical Systems and Signal Processing,2024,208: 110987.
[112]严刚,周丽.加筋复合材料结构的冲击载荷识别[J].航空学报,2008,29(5):1150‑1156.
YAN Gang,ZHOU Li. Impact load identification for stiffened composite structure[J]. Acta Aeronautics et Astronautics Sinica,2008,29(5):1150‑1156.
[113]胡锡涛,曾捷,李艳芬,等.基于粒子群‑克里金法的筒段应变场重构与载荷位置识别[J].强度与环境,2021,48(2):15‑21.
HU Xitao,ZENG Jie,LI Yanfen,et al. Reconstruction of wall strain field and static load identification of tube section based on PSO‑Kriging[J]. Structure & Environment Engineering,2021,48(2):15‑21.
[114]闫东东,胡宇博,郎利辉,等.大跨距复合材料结构弯曲载荷监测及定位方法[J].中国机械工程,2023,34(18):2257‑2267.
YAN Dongdong,HU Yubo,LANG Lihui,et al. Bending load monitoring and positioning method of long‑span composite structures[J]. China Mechanical Engineering,2023,34(18):2257‑2267.
[115]蒋祺,张方,姜金辉,等.动态载荷位置识别当量载荷误差判别法[J].振动、测试与诊断,2015,35(4):620‑625.
JIANG Qi,ZHANG Fang,JIANG Jinhui,et al. The equivalent load error method of dynamic load position determination[J]. Journal of Vibration,Measurement & Diagnosis,2015,35(4):620‑625.
[116]张景,张方,姜金辉.采用分离变量法的载荷位置识别技术研究[J].振动工程学报,2021,34(3):584‑591.
ZHANG Jing,ZHANG Fang,JIANG Jinhui. Identification of dynamic load location based on variable separation method[J]. Journal of Vibration Engineering,2021,34(3):584‑591.
[117]Liu J J,Qiao B J,Chen Y C,et al. Impact force reconstruction and localization using nonconvex overlapping group sparsity[J]. Mechanical Systems and Signal Processing,2022,162:107983.
[118]祝德春. 线弹性系统动态载荷位置识别及其实验技术研究[D]. 南京: 南京航空航天大学,2012.
ZHU Dechun. Research of dynamic load location identification and experimental technology of linear elastic system[D]. Nanjing: Nanjing University of Aeronautics and Astronautics,2012.
[119]Chen B,Hei C,Luo M Z,et al. Pipeline two-dimensional impact location determination using time of arrival with instant phase (TOAIP) with piezoceramic transducer array[J]. Smart Materials and Structures,2018,27(10): 105003.
[120]Zhao G,Hu H X,Li S X,et al. Localization of impact on composite plates based on integrated wavelet transform and hybrid minimization algorithm[J]. Composite Structures,2017,176: 234‑243.
[121]Jang B W,Kim C G. Impact localization of composite stiffened panel with triangulation method using normalized magnitudes of fiber optic sensor signals[J]. Composite Structures,2019,211: 522‑529.
[122]Datta A,Augustin M J,Gupta N,et al. Impact localization and severity estimation on composite structure using fiber Bragg grating sensors by least square support vector regression[J]. IEEE Sensors Journal,2019,19(12): 4463‑4470.
[123]Liu Q,Wang F D,Li J D,et al. A hybrid support vector regression with multi-domain features for low-velocity impact localization on composite plate structure[J]. Mechanical Systems and Signal Processing,2021,154: 107547.
[124]Thiene M,Sharif‑Khodaei Z,Aliabadi M H. Comparison of artificial neural networks and the transfer function method for force reconstruction in curved composite plates[J]. Key Engineering Materials,2015,627: 301‑304.
[125]Wen X L,Sun Q Z,Li W H,et al. Localization of low velocity impacts on CFRP laminates based on FBG sensors and BP neural networks[J]. Mechanics of Advanced Materials and Structures,2022,29(26): 5478‑5487.
[126]De Simone M E,Ciampa F,Meo M. A hierarchical method for the impact force reconstruction in composite structures[J]. Smart Materials and Structures,2019,28(8): 085022.
[127]Park B,Sohn H,Olson S E,et al. Impact localization in complex structures using laser‑based time reversal[J]. Structural Health Monitoring,2012,11(5): 577‑588.
[128]Ciampa F,Meo M. Impact localization on a composite tail rotor blade using an inverse filtering approach[J]. Journal of Intelligent Material Systems and Structures,2014,25(15): 1950‑1958.
[129]Jang B W,Kim C G. Impact localization on a composite stiffened panel using reference signals with efficient training process[J]. Composites,Part B: Engineering,2016,94B: 271‑285.
[130]Liu Q,Wang F D,Liu M X,et al. A two‑step localization method using wavelet packet energy characteristics for low‑velocity impacts on composite plate structures[J]. Mechanical Systems and Signal Processing,2023,188: 110061.
[131]李政.直升机旋翼桨叶模型分布动载荷时域识别研究[D]. 南京: 南京航空航天大学,2014.
Li Zheng. Time‑domain identification of distributed dynamic load on helicopter rotor blade model[D]. Nanjing: Nanjing University of Aeronautics and Astronautics,2014.
[132]Wang Lei,Liu Yaru. A novel method of distributed dynamic load identification for aircraft structure considering multi‑source uncertainties[J]. Structural and Multidisciplinary Optimization,2020,61(5):1929‑1952.
[133]吴邵庆,何子豪,尹健,等.星箭界面环形分布随机动载荷频域识别[J].东南大学学报(自然科学版),2022,52(5):825‑832.
WU Shaoqing,HE Zihao,YIN Jian,et al. Identification of annularly distributed random dynamic load between satellite and rocket in frequency domain[J]. Journal of Southeast University(Natural Science Edition),2022,52(5):825‑832.
[134]张开华. 运载火箭时域分段拟合动态载荷识别研究[D]. 大连: 大连理工大学,2022.
ZHANG Kaihua. Dynamic load identification of launch vehicles by time‑domain piece‑wise fitting[D]. Dalian: Dalian University of Technology,2022.
[135]尹云玉.固体火箭横向响应载荷识别方法[J].宇航学报,2009,30(6):2135‑2139.
YIN Yunyu. The identification method of transverse responding load for solid rocket[J]. Journal of Astronautics,2009,30(6):2135‑2139
[136]Zhi L H,Fang M X,Li Q S. Estimation of wind loads on a tall building by an inverse method[J]. Structural Control and Health Monitoring,2017,24(4): e1908.
[137]吴瑞犇. 基于遗传算法和神经网络的核管道载荷识别与优化研究[D]. 大连: 大连理工大学,2021.
WU Ruiben. Research on nuclear pipeline load identification and optimization based on genetic algorithm and neural network[D]. Dalian: Dalian University of Technology,2021.
[138]黄秉钧,彭涛,寇雨丰,等.基于卷积神经网络的波浪砰击载荷识别方法[J].船舶工程,2023,45(5):42‑48.
HUANG Bingjun,PENG Tao,KOU Yufeng,et al. A wave slamming load identification method based on convolution neural network[J]. Ship Engineering,2023,45(5):42‑48.
[139]吴邵庆. 基于有限元‑小波伽辽金法的车桥系统移动载荷识别[D]. 南京: 南京航空航天大学,2006.
WU Shaoqing. Moving force identification of bridge-vehicle system based on FEM and Wavelet‑Galerkin method[D]. Nanjing University of Aeronautics and Astronautics,2006.
[140]潘楚东.桥梁移动荷载与结构损伤稀疏正则化识别[D].广州:暨南大学,2018.
PAN Chudong. Sparse regularization‑based detection on moving force and structural damage of bridges[D].Guangzhou: Jinan University,2018.
[141]田瑞欣. 基于BP神经网络的桥梁移动荷载识别[D].西安:长安大学,2021.
TIAN Ruixin. Bridge moving load recognition based on BP neural network[D]. Xi’an: Chang’an University,2021.
[142]Fitzgerald P C,Sevillano E,O’Brien E J,et al. Bridge weigh‑in‑motion using a moving force identification algorithm[J]. Procedia Engineering,2017,199: 2955‑2960.
[143]胡烁.基于有限元法的连续梁移动荷载识别[D]. 石家庄: 石家庄铁道大学,2022.
HU Shuo. Moving load identification of continuous beam based on fince5706333eed7bfc3b85b45540bc0a30a9d82f687f8f1c0766f0b63817dc6ed4ite element method[D]. Shijiazhuang: Shijiazhuang Tiedao University,2022.
[144]Wang P,Yang G L,Xiao H. Dynamic load identification theoretical summary and the application on mining machinery[J]. Applied Mechanics and Materials,2013,330:811‑814.
[145]王维琴. 岩巷掘进机截割岩石动载荷识别技术的研究[D].太原:太原理工大学,2013.
WANG Weiqin. Research of cutting rock dynamic load identification for rock roadheader[D]. Taiyuan:Taiyuan University of Technology,2013.
[146]张志宏,张宏,陈有,等.基于遗传神经网络的履带行驶系统载荷识别方法[J]. 振动与冲击,2022,41(3): 54‑61.
ZHANG Zhihong,ZHANG Hong,CHEN You,et al. Load identification method of track driving system based on genetic neural network[J]. Journal of Vibration and Shock,2022,41(3): 54‑61.
[147]Liu R X,Dobriban E,Hou Z C,et al. Dynamic load identification for mechanical systems: a review[J]. Archives of Computational Methods in Engineering,2022,29(2):831‑863.
[148]巫发明. 大型双馈风电机组关键部件动力学特性分析与载荷识别研究[D].兰州:兰州理工大学,2022.
WU Faming. Dynamic characteristics analysis and load identification and verification of key components of large wind turbine[D]. Lanzhou:Lanzhou University of Technology,2022.
[149]毛文贵,李建华,郭杰,等.基于改进的信赖域模型管理技术识别风电转子系统不对中载荷[J].振动与冲击,2023,42(1):74‑80.
MAO Wengui,LI Jianhua,GUO Jie,et al. Identification of misalignment load of wind turbine rotor system based on improved trust region model management technology[J]. Journal of Vibration and Shock,2023,42(1):74‑80.
[150]宋志强,刘云贺.基于正交多项式分解的水轮机竖向动荷载识别[J].水利学报,2016,47(11):1449‑1455.
SONG Zhiqiang,LIU Yunhe. Vertical dynamic load identification of hydraulic turbine based on orthogonal polynomial decomposition[J]. Journal of Hydraulic Engineering,2016,47(11):1449‑1455.
[151]陈文博,郭惠勇.基于云模型和离散卡尔曼滤波的临时看台结构动荷载识别[J].振动与冲击,2023,42(18):233‑240.
CHEN Wenbo,GUO Huiyong. Dynamic load identification of temporary stands based on the cloud model and discrete Kalman filter[J]. Journal of Vibration and Shock,2023,42(18):233‑240.
[152]Jiang J H,Seaid M,Mohamed M S,et al. Inverse algorithm for real‑time road roughness estimation for autonomous vehicles[J]. Archive of Applied Mechanics,2020,90(6):1333‑1348.
[153]瞿伟廉,孙静,王锦文.桅杆结构动态荷载识别研究[J].武汉理工大学学报,2008,30(4):76‑79.
QU Weilian,SUN Jing,WANG Jinwen. Research on dynamic load identification of guyed mast[J]. Journal of Wuhan University of Technolog7ULeXaSmAR4YD8aQ5MGI5g==y,2008,30(4):76‑79.
[154]Yang Hongji,Jiang Jinhui,Chen Guoping,et al. Dynamic force reconstruction for structural support platforms based on the combined strategy of experiment and simulation[J]. International Journal of Structural Stability and Dynamics,2024,24(1):2450008.
Research progress on structural dynamic load identification
JIANG Jin‑hui,ZHANG Fang
(State Key Laboratory of Mechanics and Control for Aerospace Structures,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China)
Abstract: Direct measurement of dynamic loads on engineering structures is challenging due to environmental constraints. Therefore,the indirect identification or reconstruction of dynamic loads,using dynamic response information,has emerged as a highly effective method. Over decades,dynamic load identification has evolved,resulting in a series of valid solutions. This paper begins by reviewing the research history and main achievements of dynamic load identification methods. It provides a systematic exposition of typical frequency domain and time domain methods,as well as dynamic load identification methods which are based on various approaches such as function fitting,regularization strategies,Bayesian frameworks,and data-driven techniques. The advantages and disadvantages ,as well as application scope of each method,are also discussed. Additionally,this paper summarizes common issues in the load identification process,including uncertainties in structural parameters and input conditions. Identifying the position of dynamic loads is also a crucial aspect of the dynamic load identification problem. This paper analyzes the methods currently available for position identification. This paper delves into the engineering applications of dynamic load identification methods and analyzes the limitations of current methods. Considering the current challenges in the field of dynamic load identification and the increasing demands in practical engineering applications,the paper anticipates the technical difficulties that need to be addressed. It also discusses potential future development directions and key areas in dynamic load identification.
Key words: dynamic load identification;data‑driven;uncertainties;position identification;engineering applications
作者简介: 姜金辉(1981—),男,博士,教授,博士生导师。E‑mail:jiangjinhui@nuaa.edu.cn。
