基于位移PID-速度ADRC的轨迹跟随控制

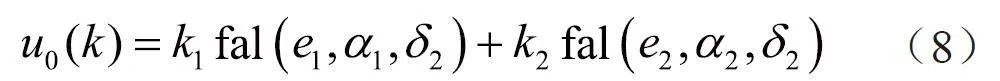
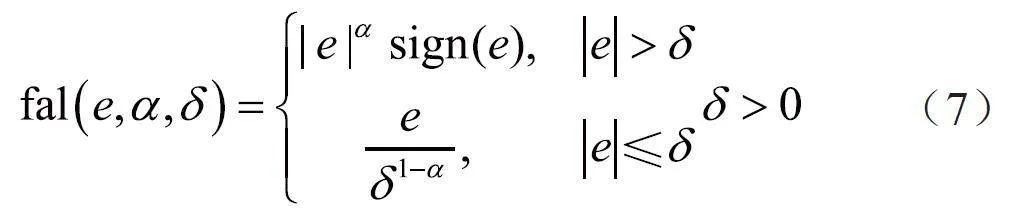
［摘 要］路径跟踪在移动机器人控制中具有重要的作用，文章针对差速轮移动机器人的轨迹跟踪控制问题，提出了一种综合纵向控制和横向控制的方法。纵向控制包括纵向位置控制和速度控制，其中纵向位置控制采用PID 控制器，通过计算实际位置与期望位置之间的差异，生成适当的控制信号，从而实现位置的调节和速度补偿。而速度控制采用自抗扰控制，引入扰动观测器和补偿器，对外界扰动进行实时估计和补偿，提高系统的鲁棒性和抗干扰能力。横向控制采用纯跟踪算法，具有简单易行、实时性好的特点，能够实现机器人与目标轨迹的高精度跟踪。试验结果表明，文章所提出的控制方法表现出优秀的性能和鲁棒性，适用于差速轮移动机器人的轨迹跟踪应用。

［关键词］移动机器人；路径跟随；自抗扰控制；纯跟踪

［中图分类号］TP273 ［文献标志码］A ［文章编号］2095–6487（2024）04–0152–03

1 概述

随着人工智能、传感技术和运动技术的进步，移动机器人能够以越来越高的精度自主移动。文章提出了一种位移PID– 速度自抗扰控制（ADRC），用于移动机器人的轨迹跟踪，该控制方法具有适应环境变化的能力。同时，文章还采用纯跟踪算法来实现机器人的横向控制，以确保控制的实时性。

2 模型建立

差速轮是一种常用于移动机器人的驱动系统，其具有简单且可靠的结构。为了实现差速轮的精确控制和路径规划，需要建立准确的差速轮运动学模型。差速轮移动机器人运动学模型为：

式中，x、y为机器人在世界坐标系下的位置坐标，θ为机器人的航向角。

在实际应用中，可以根据差速轮的几何特性和运动约束，通过数学建模和分析来推导差速轮运动学模型，从而实现对差速轮运动的控制。

3 纵向位移PID–速度ADRC闭环控制

3.1 控制框架

在差速轮移动机器人路径跟踪控制中，通常会在执行控制前进行规划。规划的目标是生成路径规划和速度规划，以实现差速轮移动机器人的准确导航。差速轮移动机器人需对参考轨迹点和速度进行跟踪控制，控制分为纵向控制和横向控制。文章设计的纵向控制结构如图1 所示。

在纵向误差控制中，采用了基于PID 控制器的纵向误差控制策略。该控制器的输入是参考点与车辆位置之间的纵向误差，输出是基于参考点处目标速度的速度补偿。这个速度补偿与目标速度相加后，作为自抗扰控制器的输入，进而计算出用于控制对象的控制量。

3.2 纵向位置PID控制

定义差速轮移动机器人与参考轨迹的纵向位置误差为e，离散化的PID 控制器表达式如下：

式中，Kp、Ki、Kd分别为PID控制器的比例系数、积分系数、微分系数。

在实际应用中，移动机器人的运动受到驱动力和外界环境的影响，导致其速度和加速度存在一定的限制，因此需要对速度和加速度进行约束。

4 纵向速度自抗扰控制

自抗扰控制能够实时估计和补偿系统中的干扰，从而提升系统的鲁棒性和抗干扰能力。ADRC 的基本结构包括以下3 个主要组成部分。

4.1 跟踪微分器

根据位移误差PID 控制输出的u（k）作为速度输入存在一些问题，如果直接将其作为速度控制的输入并采用PID 控制，可能会导致系统出现震荡或超调现象。因此，在输入速度时需要增加过渡过程来解决这些问题，跟踪微分器可提供这个过渡过程。

定义跟踪微分器为以下离散形式的系统：

式中，v（t）为目标速度；v1为跟踪速度；v2为跟踪加速度，是v（t）的近似微分；r为收敛速度；h为采样步长。

该系统的输入为v（t），输出为v1 和v2。

其中fhan（.）函数的计算方式为：

4.2 扩张状态观测器

ADRC 中的扩张状态观测器通过引入扩张状态变量来描述系统中未建模的动态特性和未知干扰，从而实现对这些因素的补偿和抑制。设计的扩张状态观测器为以下离散形式：

式中，z1为观测速度，z2为观测加速度，z3为扩张状态，y为实际速度输出，h0为采用步长，β01、β02、β03、α01、α02、b0、δ1均为可调参数。

其中函数fal（.）为：

观测器观测的状态量是z1、z2、z3，其中，调整相应的系数可得到一个观测效果较好的观测器。

4.3 非线性状态误差反馈

ADRC 中的非线性状态误差反馈（NLSEF）通过比较实际系统状态与期望系统状态之间的误差，生成非线性反馈信号，从而修正控制器的输出。对于NLSEF，先将z1 和v1 作差得跟踪速度误差e1，再将z2 和v2 作差得跟踪加速度误差e2，然后将得出的误差采用非线性组合的方式计算为控制量：

式中，k1、k2为权重系数，α1、α2、δ2均为可调参数。

最后，由u0 结合观测扰动z3（k）形成的实际控制量为u，将u 输入到移动机器人执行器中从而实现纵向控制：

5 纯跟踪算法横向控制

在横向控制中，文章采用纯跟踪算法，其是一种基于几何关系确定曲率的方法，该曲率将驱动差速轮移动机器人到达选定的路径点。目标点是已知轨迹上与当前机器人位置偏离一定距离ld 的点。假设差速轮移动机器人中心点可以按照一定的转弯半径r 到达该预瞄点，然后根据视距ld、转弯半径r 和差速轮移动机器人坐标系下预瞄点的朝向角α 之间的几何关系，确定差速轮移动机器人的转向角度，得到圆弧曲率γ与视距ld 之间的关系和角速度表达式为：

式中，x为目标点相对于机器人的横向误差。

6 仿真试验

文章对跟踪微分器的响应、扩张状态观测器的响应和双移线的轨迹跟踪进行仿真试验。

跟踪微分器及扩张状态观测器的响应试验如图2所示。由图2 可知，跟踪微分器具有较好的速度跟踪效果，并且没有高频颤振，以及扩张状态观测器对系统状态量观测有非常好的效果。

双移线的轨迹跟踪效果如图3 所示，具有较好的跟踪效果，图中不间断曲线为跟踪的双移线轨迹，“*”曲线为离散的跟踪轨迹点。

7 结束语

文章提出了一种基于纯跟踪算法的横向控制和位路径曲率的变化具有较好的适应性，能够保持良好的轨迹跟踪性能。在纵向控制方面，位移PID控制能够实现位置误差的精确控制，而速度ADRC控制则能够提供较好的鲁棒性和抗干扰能力。试验结果表明，这种组合控制策略使得移动机器人能够稳定地跟踪轨迹，具有较高的实用性。

参考文献

[1] DIANAYANAKIEV，IOANNISKANELLAKOPOULOS.Speed Tracking and Vehicle Follower Control Design forHeavy-Duty Vehicles[J].Vehicle System Dynamics，2007，25（4）：251-276.

[2] 李以农，郑玲，郝奕，等. 基于参数自整定模糊 PID 的汽车纵向控制[J]. 江苏大学学报（自然科学版），2006，27（1）：22-26.

[3] RIVERA D E，MORARI M，SKOGESTAD S .Internalmodel control ：PID controller design[J].Industrial &Engineering Chemistry Process Design & Development，1986，25（1）：2163.

[4] 曹杰华. 一种基于纯跟踪算法的单舵轮AGV 路径跟随方法及系统：CN202210562076.8[P].2022-09-02.

[5] 靳欣宇，张军，刘元盛，等. 基于Stanley 算法的自适应最优预瞄模型研究[J]. 计算机工程，2018，44（7）：42-46.

[6] 许万，曹松，罗西，等. 双轮差速移动机器人轨迹跟踪混合控制算法研究[J]. 组合机床与自动化加工技术，2018（3）：78-83.

[7] 韩京清. 从PID 技术到“自抗扰控制”技术[J]. 控制工程，2002（3）：13-18.