压电纳米声子晶体梁结构表面效应带隙特性研究

摘"要： 通过纳米尺寸下的纯弹性材料环氧树脂和压电材料PZT-4沿着轴向周期性交替排布，提出了压电纳米声子晶体梁结构的力学模型.将表面压电理论与Euler梁理论相结合，结合平面波展开法，建立了计算该模型能带结构的表面效应平面波展开法.进一步地，外加电压和外加轴力被用来研究机电耦合效应对带隙的影响，残余面应力和材料内禀长度被用来研究表面效应对带隙的影响，以及晶胞内PZT-4对环氧树脂的长度比和高宽比被用来研究几何参数对带隙的影响.研究结果和进一步的分析表明，影响规律对基于压电纳米声子晶体梁的纳米机电系统的设计过程和主动控制将起到积极的推动作用.

关键词： 压电纳米声子晶体梁；平面波展开法；表面效应；机电耦合效应

中图分类号：TB535"""文献标志码：A"""""文章编号：1673-4807（2024）04-025-07

Study on bandgap properties of a piezoelectric phononiccrystal nanobeam with surface effects

QIAN Denghui，LIU Guoqing，ZHANG Zexin，GE Haoran，ZOU Peng

（School of Naval Architecture amp; Ocean Engineering， Jiangsu University of Science and Technology， Zhenjiang 212100， China）

Abstract：The model of piezoelectric phononic crystal nanobeam is proposed by periodically repeating elastic material epoxy and piezoelectric material PZT-4 at nanoscale along the axial direction. The plane wave expansion method with surface effects is derived and formulized by coupling surface piezoelectric theory， Euler beam theory and traditional plane wave expansion method to calculate the corresponding band structures. Moreover， the external electrical voltage and axial force are chosen to investigate the influences of electro-mechanical coupling effects on band gaps. Residual surface stress and material intrinsic length are picked as the influencing parameters related to surface effects. Ratio of the length of PZT-4 to that of epoxy in a unit cell and the height-width ratio are chosen to research the effects of geometric parameters on band gaps. The results and analysis are expected to be helpful in designing piezoelectric nanobeam-based devices.

Key words：piezoelectric phononic crystal nanobeam， plane wave expansion method， surface effect， electro-mechanical coupling effect

作为一种人造周期性复合弹性结构，近三十年来，形式各异的声子晶体以其独有的弹性波/声波带隙特性吸引了广大国内外专家学者的关注［1］.针对工程中比较常用的杆、梁、单板以及双层板等基本弹性结构，传统声子晶体的设计思路可以被引入其中从而满足相应的工程需求［2］.此外，基于多物理场耦合下的声子晶体也获得了一定的研究，比如压磁声子晶体、压电声子晶体、磁电弹声子晶体等［3-4］.其中，压电声子晶体基于机械场和电场之间的相互转换实现对带隙的有效调控，并进一步基于电场对带隙的调节规律实现对带隙的主动控制.上述声子晶体结构均是处于宏观尺寸，相应带隙频段所对应的量级一般是从赫兹（Hz）到兆赫（MHz）之间.近年来，随着纳米技术在各领域的迅猛发展，开始涌现出一批对纳米尺寸的新型声子晶体结构的研究［5］，这使得所获带隙频段对应的量级急剧上升到千兆赫（GHz）甚至太兆赫（THz）.综上所述，若将压电材料与纳米材料相结合并引入到声子晶体中构成压电纳米声子晶体结构，将汇聚压电材料、纳米材料以及声子晶体的优良特性为一体，并能通过各组分之间相互耦合展现出新的物理性能.对压电纳米声子晶体结构的深入研究将促进新型压电纳米器件的产生，并为纳米机电系统应用提供新的可能.

压电纳米声子晶体结构所展现的带隙特性及其后续主动控制研究均离不开行之有效的带隙计算方法.就目前而言，国内外文献中只出现少量对压电纳米声子晶体结构的直接性研究.文献［6］基于非局部理论的传递矩阵法，考虑材料的内部特征尺寸，对一维层状压电纳米声子晶体结构的平面波模态进行了详细的研究.文献［7］应用平面波展开法对多种晶格分布下的不同形状散射体所构成的二维压电纳米声子晶体的能带结构进行了计算，并对相应带隙特性展开了研究.但是近年来，有关压电纳米结构的力学性能和宏观声子晶体的带隙特性已经获得了一定的研究.

对于宏观尺寸结构，大量实验和工程案例已经证明，经典连续介质力学理论可以被成熟有效地用来研究不同结构的力学性能.但是对于纳米量级结构，已有研究表明大多数与材料相关特性以及力学性能均表现出明显的尺寸依赖性，这就导致广泛应用的宏观连续介质力学理论难以继续适用.但基于此经典力学理论，通过进行修正，学者们提出了一些高阶连续介质力学理论.其中，比较常用的有：表面弹性理论、非局部弹性理论、偶应力弹性理论以及应变梯度弹性理论［8-11］等.对于上述高阶连续介质力学理论，目前均开展了大量研究，各理论均存在一定的不足及自身的适用性.对于纳米尺度下的梁板结构，表面弹性理论的适用性已被广泛证明.表面弹性理论是由文献［12］首次提出，该理论假设研究对象是由块体和表面层两部分构成，并且表面层被假设为无厚度的薄膜且无滑移地粘贴在块体上.因此，块体和表面层中的基本方程显然会有所区别.基于此理论，近年来出现大量关于表面效应对不同纯弹性纳米结构的各种力学特性的影响研究［13］.但对于压电纳米结构，传统表面弹性理论不能直接适用.通过在表面弹性理论中考虑表面压电和表面介电性能的影响，文献［14］建立了表面压电模型.目前，该模型已被广泛用于研究各类压电纳米结构相关力学特性.基于Kirchhoff板模型，文献［15］将表面压电理论引入到压电纳米板中，并对该板的振动响应和机电耦合特性展开研究.基于Timoshenko梁模型和表面压电模型，文献［16］对集中力作用下的压电纳米梁的弯曲挠度和共振频率进行了详细推导.结果表明表面压电性和表面残余应力对压电纳米梁弯曲和振动行为的影响非常显著.基于表面压电理论，文献［17］对纤维増强型压电纳米薄膜在反平面剪切变形下的机电耦合行为展开了研究，并进一步讨论了表面效应和纤维形状对材料宏观机电耦合行为的影响机制.

对于宏观声子晶体能带结构计算方法的研究，目前比较成熟的有平面波展开（PWE）法［1］、传递矩阵（TM）法［18］、有限元（FE）法［19］等.针对不同类型的声子晶体结构，上述方法均有其各自的适用范围.由于本项目在带隙计算这一环节是基于平面波展开法而展开的，所以这里对该方法稍做详细介绍.平面波展开法是基于声子晶体特有的结构周期性，将密度、弹性常数等结构参数以及位移场以空间傅里叶级数进行展开并截断，再与Bloch定理相结合，从而将能带结构的计算化为广义特征值问题的求解.研究表明，平面波展开法对于只包含固体或流体的声子晶体具有非常好的适用性［20］.通过进一步结合超胞技术并考虑空间傅里叶级数展开的平移对称性，该方法同样可被应用于带有缺陷的声子晶体［21］.平面波展开法最常被诟病的问题便是收敛性，对于组元结构参数相差较大的声子晶体，一般可以采用改进平面波展开法来提高收敛效果［22］.但是，平面波展开法对由固体和流体（或流体）混合而成的声子晶体不具备适用性［1］.

在众多科研人员对压电纳米结构以及声子晶体结构的研究基础上，文中通过在压电纳米梁中引入声子晶体设计思路从而构成压电纳米声子晶体梁结构.结合表征压电纳米梁的表面压电理论以及计算声子晶体能带结构的平面波展开法，从而提出兼具机电耦合效应、表面效应的压电纳米声子晶体梁结构带隙计算方法，并建立该结构所特有的带隙特性.

1"模型和方法

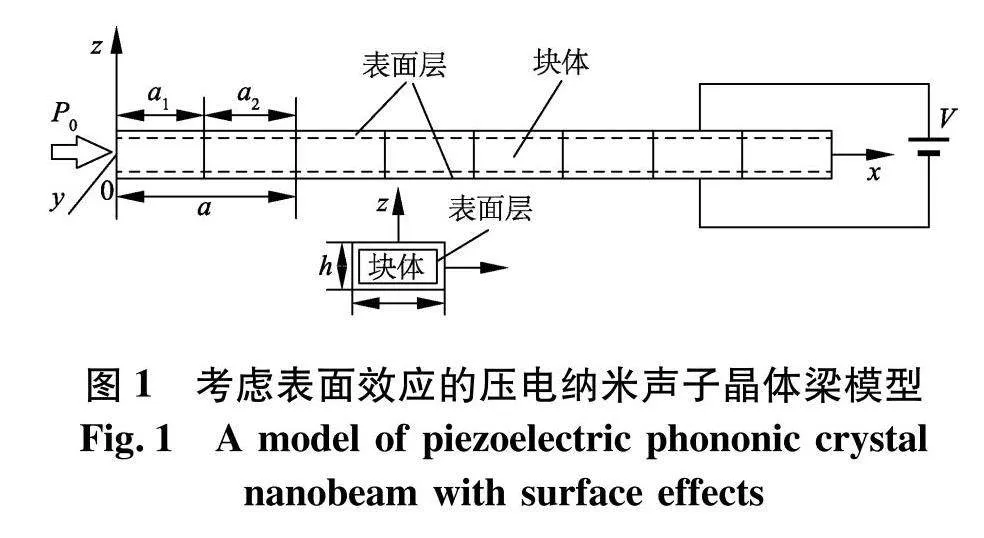
如图1，矩形截面压电纳米声子晶体梁结构由压电材料PZT-4和弹性材料环氧树脂周期交替构成.以轴向为x轴，宽度方向为y轴以及高度方向为z轴建立笛卡尔坐标系，如图所示.其中，施加在PZT-4上的外加电场为V，外加轴向力为P0.一个晶胞内的PZT-4和环氧树脂长度分别为a1和a2，因此晶格常数为a=a1+a2.对于截面，宽度和高度分别为b和h.此外，材料之间的界面效应忽略不计，且考虑表面效应存在于纳米梁的表面，这就导致梁被分为块体和表面层两部分.

假设宽度b和高度h远小于晶格常数a，根据Euler-Bernoulli梁理论，轴向应变εx与位移w（x，t）之间的关系可以写为：

εx=-z2w（x，t）x2（1）

假设电场Ez仅仅存在于z向，跟电势φ之间的关系可以表示为：

Ez=-φz（2）

对于PZT-4的块体部分，机电耦合本构方程可以写为：

σx=c11εx-e31Ez（3）

Dz=e31εx+κ33Ez（4）

式中：σx为轴向应力；Dz为z向电位移；c11、e31和κ33分别为弹性常数、压电常数和介电常数.

对于PZT-4的表面层部分，本构方程可以写为［12］：

σsx=σ0x+cs11εsx-es31Esz（5）

Dsz=D0z（6）

式中：σsx和εsx分别为表面应力和表面应变；Dsz和Esz分别为表面电位移和表面电场；σ0x和D0z分别为残余表面应力和残余表面电位移；cs11和es31分别为表面弹性常量和表面压电常量.

忽略自由电荷，由高斯定律可得：

Dzz=0（7）

由式（1、2、4、7），并且考虑电场边界条件φ-h2=0和φh2=V，可以求得电势为：

φ=-e312κ332w（x，t）x2z2-h24+Vhz+V2（8）

将式（2、8）代入到（3、5）中，PZT-4块体和表面层中的轴应力可以由弯曲位移分别表示为：

σx=e31Vh-c11+e231κ33z2w（x，t）x2（9）

σsx=σ0x+es31Vh-cs11+es31e31κ33z2w（x，t）x2（10）

对于环氧树脂的块体部分，弹性本构方程可以写为：

σx=Eεx（11）

式中，E为弹性模量.

对于环氧树脂的表面层部分，本构方程可以写为：

σsx=σ0x+Esεsx（12）

式中，Es为表面弹性模量.

将公式（1）代入到（11、12），环氧树脂块体和表面层中的轴应力可以由弯曲位移分别表示为：

σx=-Ez2w（x，t）x2（13）

σsx=σ0x-Esz2w（x，t）x2（14）

所有的表面层参数跟体块相应参数具有一定的对应关系：

pslspb（15）

式中：ps和pb分别为表面层和块体中相应参数；ls为材料内禀长度.

根据广义Young-Laplace方程以及一系列公式推导［8］，考虑表面效应的纳米梁振动控制方程可以写为：

2Mx2-P2w（x，t）x2-x∫STxzdS-∫STzdS=

-ρA2w（x，t）t2（16）

式中：M=-∫AσxzdA和P=P0+∫AσxdA分别为弯矩和轴力；Tx=σsxx和Tz=σsxRc分别为表面应力引起的牵引力跳跃；Rc为曲率半径，并且Tz仅仅作用于梁的顶面和底面；S和A分别为截面的周长和面积；ρ为材料密度.

将式（9，10）代入到式（16）中，并且考虑振动为简谐的，最终考虑表面效应的压电纳米梁振动控制方程可以用弯曲位移表示为：

2x2bh312c+bh22+h36cs2w（x）x2-

2bσ0x+2bes31Vh+be31V2w（x）x2=ω2ρ1Aw（x）（17）

式中：c=c11+e231/κ33，cs=cs11+es31e31/κ33；ρ1为PZT-4的密度.

类似地，将式（13、14）代入到式（16）中，可以得到考虑表面效应的弹性纳米梁振动控制方程：

2x2bh312E+bh22+h36Es2w（x）x2-2bσ0x2w（x）x2=ω2ρ2Aw（x）（18）

式中，ρ2为环氧树脂的密度.

定义：

m1（x）=bh312c+bh22+h36cs（19）

n1（x）=2bσ0x+2bes31Vh+be31V（20）

p1（x）=ρ1A（21）

m2（x）=bh312E+bh22+h36Es（22）

n2（x）=2bσ0x（23）

p2（x）=ρ2A（24）

此外，应用m（x），n（x）和p（x）分别为（m1（x），m2（x）），（n1（x），n2（x））和（p1（x），p2（x）），式（17、18）可以统一写为：

2x2m（x）2w（x）x2-n（x）2w（x）x2=ω2p（x）w（x）（25）

由于压电纳米声子晶体梁在轴向的材料周期性，m（x），n（x）和p（x）可以展开成空间傅里叶级数形式：

ξ（x）=∑Gξ（G）eiGx（26）

其中，

ξ（G）=ξ2f+ξ1（1-f）""G=0

（ξ2-ξ1）ψ（G）G≠0（27）

式中：ξ（x）被用来统一表示m（x），n（x）和p（x）；ξ1和ξ2分别为PZT-4的相应参数；f=a2/a表示环氧树脂的填充率.此外，ψ（G）=fsin（Ga2/2）/（Ga2/2），且G为一维倒格矢.

根据Bloch定理和结构的周期性，w（x）可以表示为：

w（x）=∑G′wk（G′）ei（k+G′）x（28）

式中，k为不可约Brillouin区的边界上的Bloch波矢.

将公式（26，28）代入到式（25）中，并且考虑倒格矢的个数为N，则可以得到：

（MG+NG-ω2PG）×（w（G））=0（29）

其中，

（MG）ij=（k+Gi）2m（Gi-Gj）（k+Gj）2（30）

（NG）ij=n（Gi-Gj）（k+Gj）2（31）

（PG）ij=p（Gi-Gj）（32）

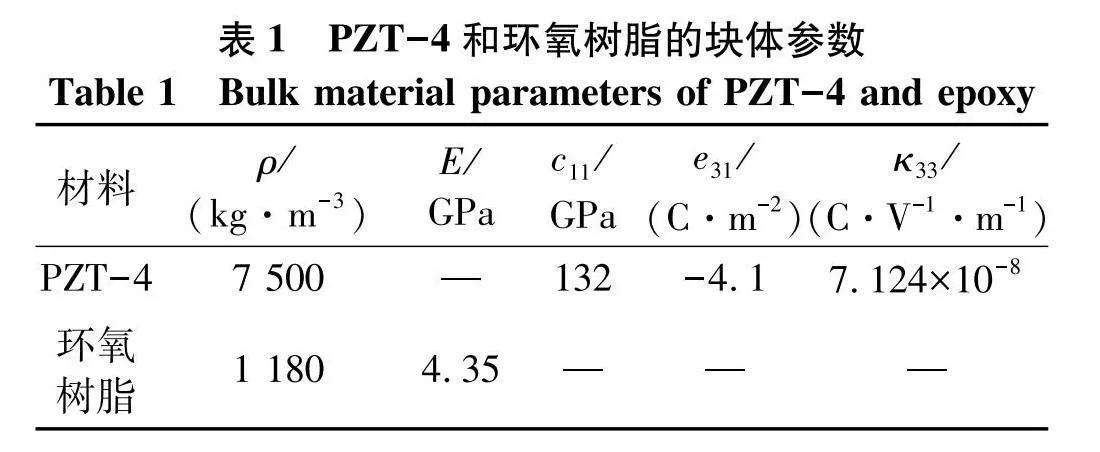
式（29）表示一个关于ω2的广义特征值问题.通过求解每一个Bloch波矢下的该方程，可以最终得到该压电纳米声子晶体梁的表面效应能带结构.PZT-4和环氧树脂的块体参数如表1［13］，且相应的表面层参数可以通过式（15）求得.

表1"PZT-4和环氧树脂的块体参数

Table 1"Bulk material parameters of PZT-4 and epoxy

材料ρ/（kg·m-3）E/GPac11/GPae31/（C·m-2）κ33/（C·V-1·m-1）

PZT-47 500—132-4.17.124×10-8

环氧树脂1 1804.35———

2"结果和分析

2.1"能带结构

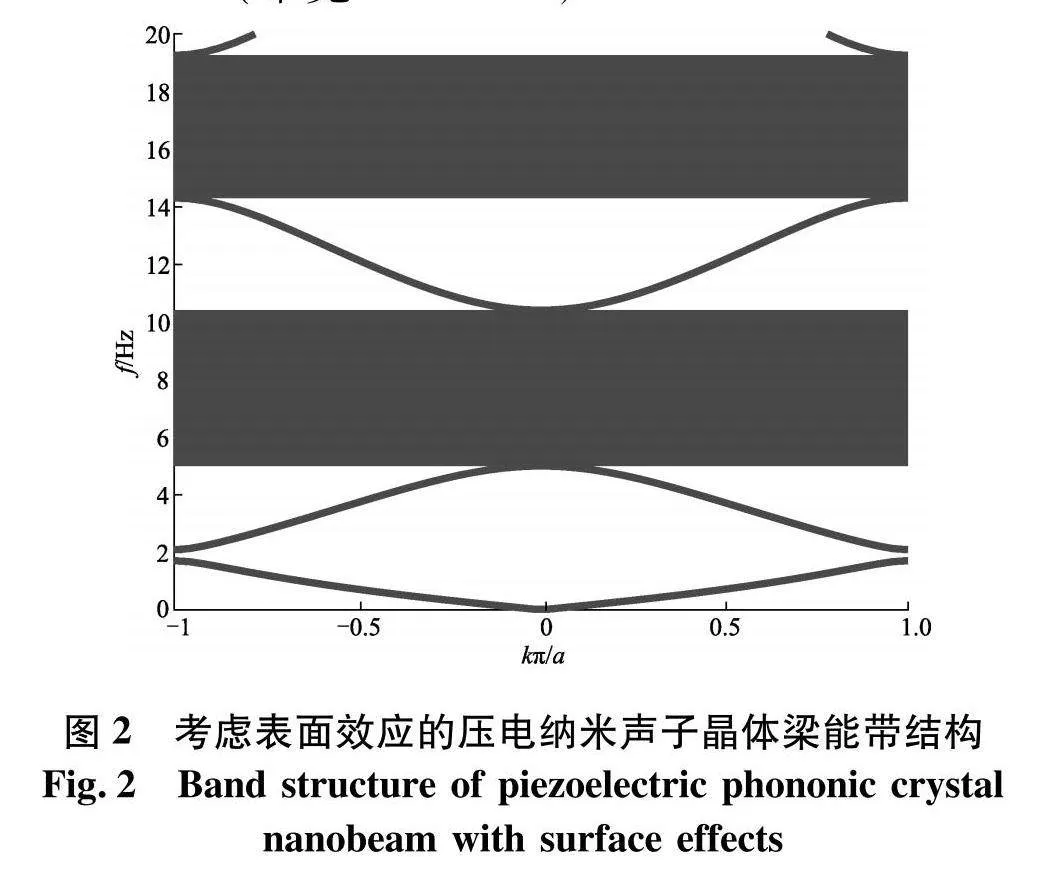
图2为考虑表面效应的压电纳米声子晶体梁能带结构.计算过程中，所有材料参数如表1.几何参数：a1=a2=50 nm，b=h=10 nm；表面层参数：σ0x=1 N·m-1，ls=1 nm.此外，外加电压：V=0.2 V，外加轴向力为：P0=1×10-8 N.为了满足收敛性需求，选用N=2×50+1个平面波数.从图中可以看出，20 GHz以下可以打开好几条完整带隙.在这里，前两阶带隙被选用研究其带隙特性，分别是1.71～2.09 GHz（带宽0.38 GHz）以及4.99～10.41 GHz（带宽5.42 GHz）.

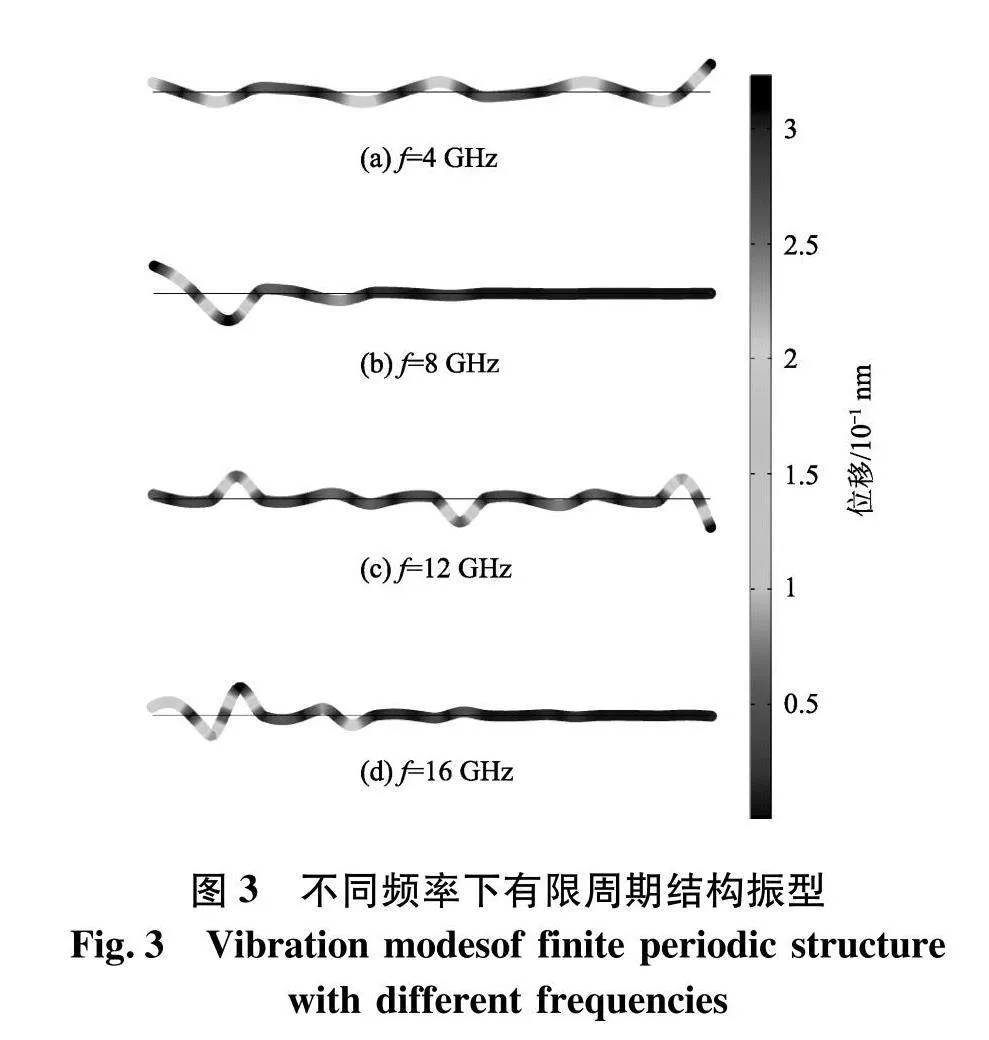
为了进一步揭示带隙和通带频段所对应的振动性质，图3给出了不同带隙和通带频段下的相应有限结构振型.此处，选用了4个频率，分别为4，8，12、16 GHz.从图2可以看出，4、12 GHz分别落在第二和第三条通带频段内，8 GHz和16 GHz分别落在第二和第三阶带隙频段内.此外，有限结构基于声子晶体晶胞，共选用了5个周期.材料和几何参数与图2一致，激励点和响应点分别选择梁的两端.从图3可以看出，当频率落在通带频段内，振动可以无阻碍地沿着梁向前传播.但是，当频率落在带隙频段内，振动会迅速衰减而无法进一步向前传播.基于压电纳米声子晶体梁的通带和带隙特性，以及通带和带隙频段均处于GHz量级，该结构在超高频谐振器、滤波器等声学和振动器件上拥有非常广阔的应用前景.

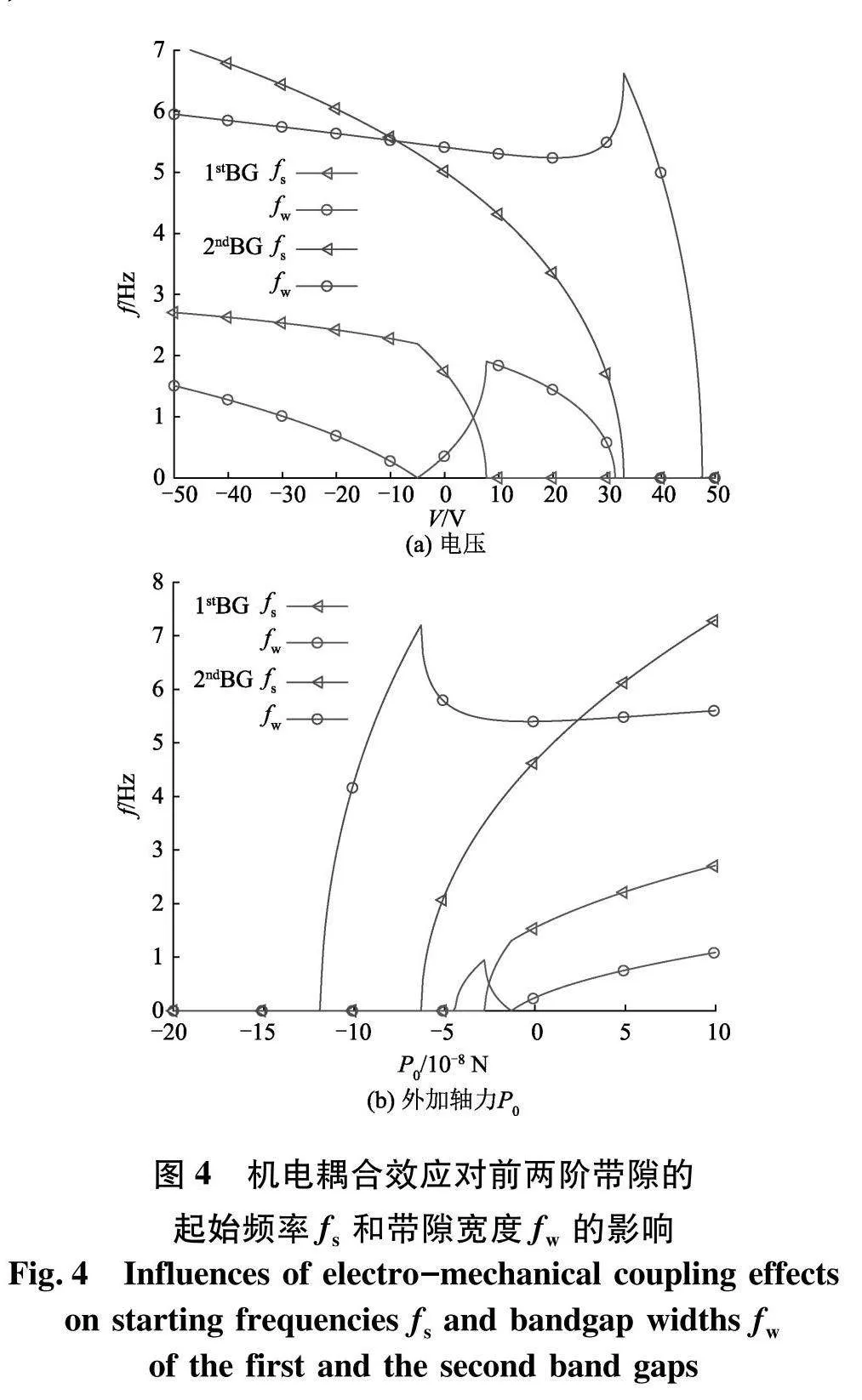
2.2"机电耦合效应对带隙的影响

电压V对前两阶带隙的起始频率fs和带隙宽度fw的影响如图4（a）.算例中除了V以外其余参数均与图2中一致，且V的区间从-50～50 V.对于前两阶带隙的变化规律相似.均是随着电压的变大，起始频率一直在降低直到为0，而带隙宽度先减后增再减小，最终也是趋于0.因此，为了满足工程上对带隙一定宽度的需求，电压要尽量避免太大且在峰值对应电压附近调节.

图4（b）给出了外加轴力P0对前两阶带隙的起始频率fs和带隙宽度fw的影响.除了P0以外其余参数均与图2一致，且P0的区间从-20×10-8 N到10×10-8 N.如图，外加轴力P0对前两阶带隙的影响是类似的，且恰好跟电压V相反.随着P0的增加，起始频率从0开始一直增加，而带隙宽度从0开始先增后减再增加.所以，为了达到一定的带隙宽度，外加轴力要尽量避免太小且在峰值附近调节.

此外，从图4中可以看出，参数对带隙起始频率的影响较为规律，而对带隙宽度的影响存在突变.这是因为带隙宽度是由带隙截止频率和起始频率之差求得，而随着参数的变化，带隙起始和截止频率所在能带往往会发生变化.

2.3"表面效应对带隙的影响

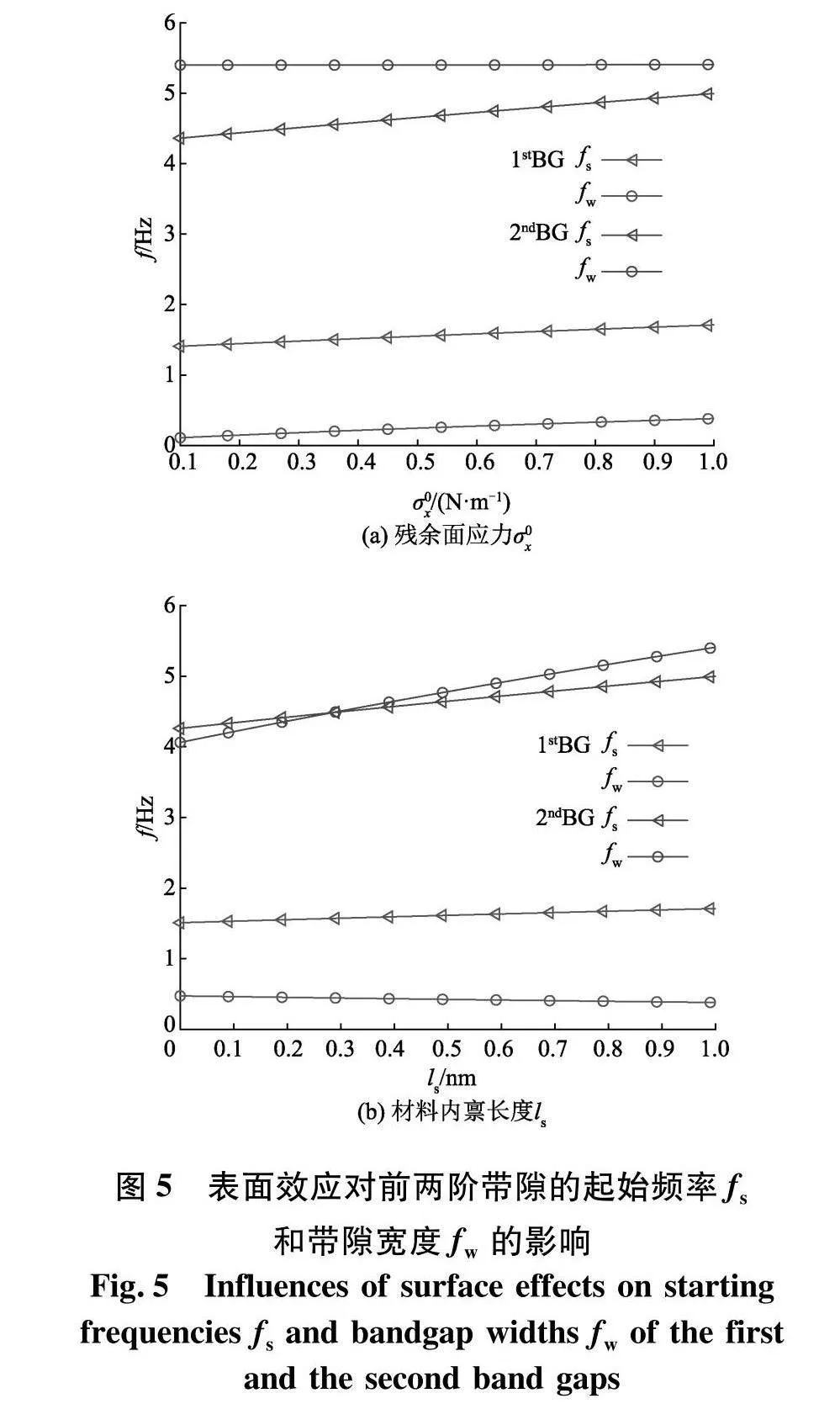
表面效应主要由残余面应力σ0x和材料内禀长度ls来表征.σ0x对前两阶带隙的起始频率fs和带隙宽度fw的影响如图5（a）.除σ0x以外所有参数均与图2一致，且σ0x的区间为0.1 N·m-1到1 N·m-1，这归因于典型的残余面应力就是在该区间取值［8］.对于前两阶的起始频率和带隙宽度，均是随着残余面应力的增加而增加.但σ0x对第二阶带隙的宽度影响很小，几乎可以认为保持不变.

图5（b）给出了材料内禀长度ls对前两阶带隙的起始频率fs和带隙宽度fw的影响.除ls以外所有参数均与图2一致，且ls的区间为0～1 nm.对于第一阶带隙的起始频率以及第二阶带隙的起始频率和带隙宽度，均是随着材料内禀长度的增加而增加.但是，随着材料内禀长度的增加，第一阶带隙的宽度反而一直减小.

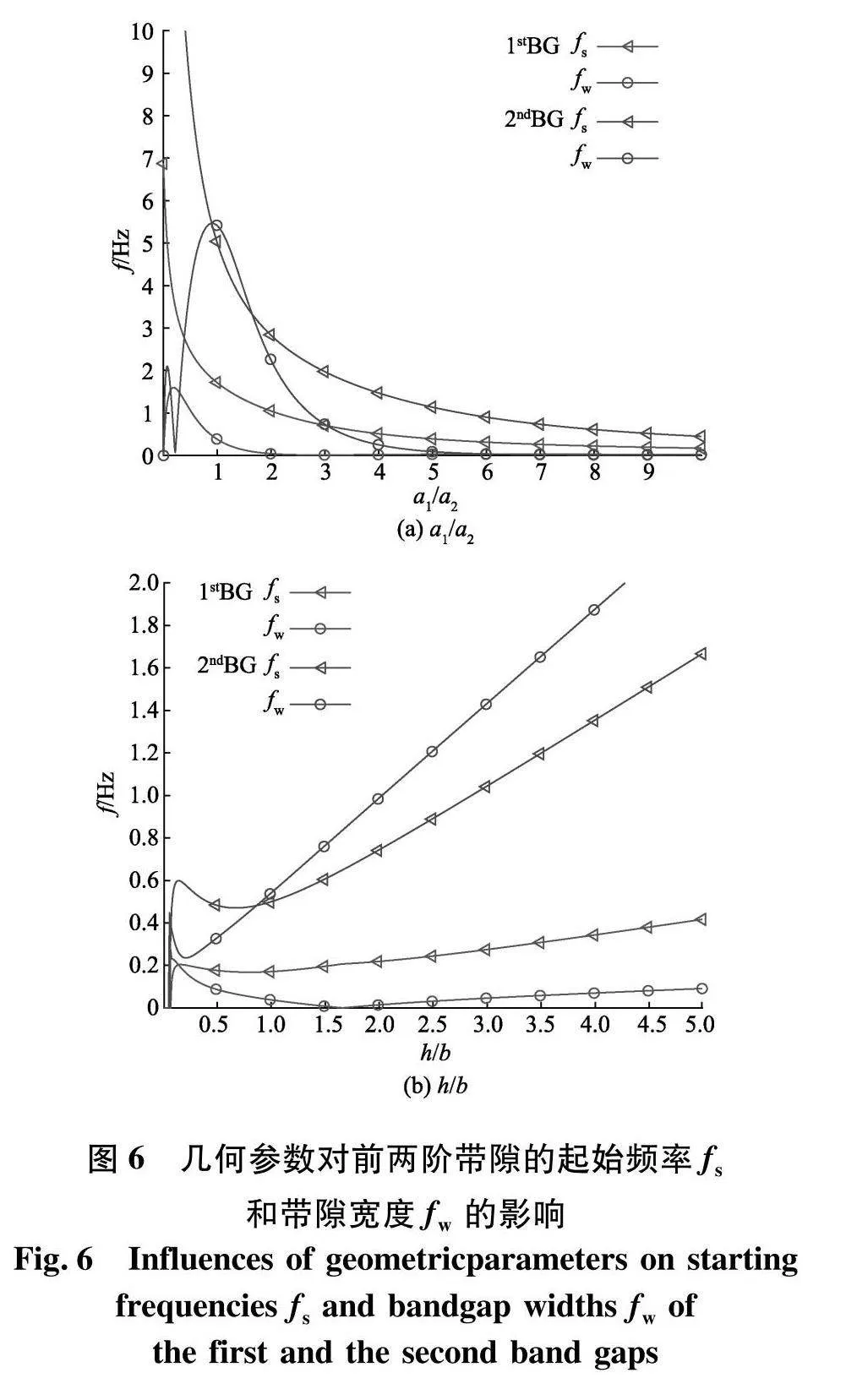
2.4"几何参数对带隙的影响

为了研究几何参数对带隙的影响，晶胞内PZT-4和环氧树脂的长度比a1/a2和高宽比h/b被选作影响因子.图6（a）和（b）分别给出了a1/a2和h/b对前两阶带隙的起始频率fs和带隙宽度fw的影响.对于起始频率，两阶带隙的影响规律类似：随着a1/a2的增加，均是逐渐降低至0；随着h/b的增加，起始频率呈现出先增加后降低再增加的趋势.但是对于带隙宽度，随着a1/a2的增加，第一阶和第二阶带隙分别经历一个和两个峰值之后逐渐降至0；随着h/b的增加，两阶带隙均是经历一个峰值之后再逐渐增大.

因此，在设计压电纳米声子晶体梁的过程中，带宽峰值所对应的长度比和高宽比可以被选用以达到使得带隙尽可能宽的目的.

3"结论

通过无限周期重复压电材料和弹性材料构造了一个压电声子晶体梁模型.基于表面弹性理论、Euler梁理论和平面波展开法，计算了该模型的能带结构.基于能带结构图和振型图分析，当频率落在通带频段内，振动可以无阻碍地沿着梁向前传播.但是，当频率落在带隙频段内，振动会迅速衰减而无法进一步向前传播.因此，该结构在超高频声学和振动器件领域拥有广阔前景.此外，从机电耦合效应、表面效应和几何参数3个角度分析了带隙的影响规律.

（1） 随着外加电压的增大或者外加轴向力的减小，第一阶和第二阶带隙均是起始频率逐渐降低至零，而带隙宽度先减后增再减小，最终趋于零；

（2） 随着残余面应力的增加，两阶带隙起始频率和带隙宽度均增加；而随着材料内禀长度的增加，第一阶带隙的起始频率以及第二阶带隙的起始频率和带隙宽度均增加，而第二阶带隙的宽度减小.

（3） 随着晶胞内PZT-4和环氧树脂长度比的增加，第一阶和第二阶带隙起始频率均逐渐降低至零，而带隙宽度分别经历一个和两个峰值之后逐渐降至零；随着高宽比的增加，两阶带隙起始频率和带隙宽度均呈现出先增加后降低再增加的趋势.

参考文献（References）

［1］"温华兵， 李军， 李兵. 质量块-支架梁局域共振板结构的低频振动带隙特性研究［J］. 江苏科技大学学报（自然科学版）， 2019， 33（3）： 43-48.

［2］"CHUANG Kuochi， YUAN Zhiwen， GUO Yongqiang， et al. A self-demodulated fiber Bragg grating for investigating impact-induced transient responses of phononic crystal beams［J］. Journal of Sound amp; Vibration， 2018， 431： 40-53.

［3］"QIAN Denghui， SHI Zhiyu. Bandgap properties in locally resonant phononic crystal double panel structures with periodically attached spring-mass resonators［J］. Physics Letters A， 2016， 380（41）： 3319-3325.

［4］"孙炜海， 张超群， 鞠桂玲， 等. 含磁电弹夹层的压电/压磁声子晶体带隙特性研究［J］. 物理学报， 2018， 67（19）： 194303.

［5］"WAGNER M R， GRACZYKOWSKI B， REPARAZ J S， et al. Two-dimensional phononic crystals： disorder matters［J］. Nano Letters， 2016， 16（9）： 5661.

［6］"YAN Dongjia， CHEN Ali， WANG Yuesheng， et al. In-plane elastic wave propagation in nanoscale periodic layered piezoelectric structures［J］. International Journal of Mechanical Sciences， 2018（142/143）： 276-288.

［7］"MIRANDA J E， SANTOS J M C. Complete band gaps in nano-piezoelectric phononic crystals［J］. Materials Research， 2017， 20： 15-38.

［8］"YAN Zhi， JIANG Liying. The vibrational and buckling behaviors of piezoelectric nanobeams with surface effects［J］. Nanotechnology， 2011， 22（24）： 245703.

［9］"LIU Chen， KE Liaoliang， WANG Yuesheng， et al. Thermo-electro-mechanical vibration of piezoelectric nanoplates based on the nonlocal theory［J］. Composite Structures， 2013， 106（12）： 167-174.

［10］"MINDLIN R D， TIERSTEN H F. Effects of couple-stresses in linear elasticity［J］. Archive for Rational Mechanics amp; Analysis， 1962， 11（1）： 415-448.

［11］"LAM D C C， YANG F， CHONG A C M， et al. Experiments and theory in strain gradient elasticity［J］. Journal of the Mechanics amp; Physics of Solids， 2003， 51（8）： 1477-1508.

［12］"GURTIN M E， MURDOCH A I. A continuum theory of elastic material surfaces［J］. Archive for Rational Mechanics amp; Analysis， 1975， 57（4）： 291-323.

［13］"李郑梁， 庞苗. 考虑高阶表面效应的非局部纳米板屈曲分析［J］. 科技通报， 2018， 34（5）： 7-10.

［14］"HUANG Ganyun， YU Shouwen. Effect of surface piezoelectricity on the electromechanical behaviour of a piezoelectric ring［J］. Physica Status Solidi， 2006， 243（4）： 22-24.

［15］"YAN Zhi， JIANG Liying. Surface effects on the electroelastic responses of a thin piezoelectric plate with nanoscale thickness［J］. Journal of Physics D Applied Physics， 2012， 45（25）： 1-5.

［16］"XU Xiaojian， DENG Zichen， WANG Bo. Closed solutions for the electromechanical bending and vibration of thick piezoelectric nanobeams with surface effects［J］. Journal of Physics D Applied Physics， 2013， 46（40）： 405302.

［17］"FANG Xueqian， HUANG Mingjuan， ZHU Zitao， et al. Surface free energy effect on electro-mechanical behavior of piezoelectric thin film with square nanofibers under anti-plane shear［J］. Acta Mechanica， 2015， 226（1）： 149-156.

［18］"张振国， 耿晓雯， 刘英， 等. 一维二组元声子晶体结构参数的传递矩阵法反演研究［J］. 噪声与振动控制， 2017， 37（4）： 185-187.

［19］"吴吉恩， 胡瑞霞， 邓科. 压电声子晶体能带结构的有限元方法模拟［J］. 吉首大学学报（自然科学版）， 2018， 39（3）： 31-34.

［20］"HUANG Jiankun， SHI Zhifei. Attenuation zones of periodic pile barriers and its application in vibration reduction for plane waves［J］. Journal of Sound amp; Vibration， 2013， 332（19）： 4423-4439.

［21］"LI Xiaochun， LIU Zhengyou. Coupling of cavity modes and guiding modes in two-dimensional phononic crystals［J］. Solid State Communications， 2005， 133（6）： 397-402.

［22］"CAO Yongjun， HOU Zhilin， LIU Youyan. Convergence problem of plane-wave expansion method for phononic crystals［J］. Physics Letters A， 2004， 327（2/3）： 247-253.

（责任编辑：贡洪殿）