基于黏粒含量的黄河下游堤防土水特征曲线预测研究

关键词：土水特征曲线；黏粒含量；围压；黄河下游堤防

黄河下游堤防大多由民埝多次培厚加高而成，虽然新近加固时已有相关规范标准，但其堤身土体级配差别较大。此外，受黄河流域气候的影响，黄河下游堤防土体长期处于季节性干湿交替状态，土体含水量的变化会引起堤身及堤基强度降低、结构变形，存在堤防开裂、堤身蛰坑等安全隐患，遭遇强降雨时．甚至造成背河堤坡严重垮塌等险情。土水特征曲线（SoilWater Characteristic Curve，简称SWCC）是描述土中含水量与基质吸力关系的曲线，也可描述非饱和土水一力一化耦合过程，土的渗透、强度和变形等力学特征都与SWCC密切相关。因此，研究黄河下游堤防土体的SWCC变化规律对堤防稳定性评价、汛期堤防重点查勘与加固等具有重要的现实指导意义。

早期研究SWCC的方法大体可分为两类：一类是通过不同试验仪器或测试方法进行实测，称为直接测定法，如常见的压力板仪法、张力计法、滤纸法、蒸汽平衡法、冷镜露点法等，不同的方法适用于不同的吸力范围。研究者常采用多种方法相结合的方式获得宽广吸力范围的土水特征曲线，并在研究中不断探寻可降低试验难度及耗时的测定方法。另一类是采用经验公式或不同形式的数学模型进行研究，比较经典的测算模型有Gardner模型、Brooks-Corey模型、Van Genuchten模型、FX模型等，这些模型大多基于经验、土体孔径分布以及曲线的形状特征所建立。随着对岩土体的深入研究，人们认识到土体孔径分布及颗粒表面等都存在分形特征，加之经典测算模型存在幂函数、对数函数特征，因此有学者利用分形理论来预测土水特征曲线。

目前用于直接测量的试验方法仍有耗时长、成本高、数据离散等缺点，而已有的测算模型依赖较多特征参数，尤其是描述孔径分布的特征参数往往需要压汞法或其他技术（如核磁共振、CT）测量孔径分布曲线，其时间长、成本较高。此外，黄河下游堤防多为堤路结合方式，而对于非饱和土体在荷载作用下的含水量与基质吸力之间的关系目前虽有初步认识，但针对不同围压条件下的定量测算模型、模型参数对应的物理意义等还需进一步研究。

为此，本文以黄河下游堤防土样为研究主体，通过分析不同土质的土水特征曲线，以黏粒含量与干密度为指标，探求适用于黄河下游堤防非饱和土土水特征曲线的简易测算模型，并根据实测含水量与基质吸力的关系，拓展该简易模型用来描述黄河下游堤防不同围压下的土水特征曲线，以期为黄河下游堤防堤基抗剪强度、非饱和渗透以及堤防边坡稳定性评价等提供方便、快捷的土水特征曲线测算方法。

1黄河下游堤防概况及数据收集

1.1黄河下游堤防概况

黄河堤防与骨干水库、河道工程以及滞洪区共同组成了黄河现状防洪工程体系。黄河下游堤防随着河道变迁经历代不断修建而成，新中国成立以来，黄河下游进行了三次大规模修堤，时间分别为1950-1957年、1962-1965年、1974-1985年，并于1996年启动黄河标准化堤防工程建设，对堤防堤身进行标准化帮宽加固。目前，黄河下游临黄大堤长1371.2km，其中：左岸从孟州市中曹坡至利津四段，长747.0km;右岸从邙山头至垦利二十一户，长624.2km（含孟津堤7.6km）。

黄河下游堤防在原有民埝基础上多次加高加固，加上下游河道善淤多变，导致早期就地取土修筑的堤身土体组成复杂，大体可分为黏土、壤土、砂壤土、粉土、粉砂、极细砂以及砂土七大类土鉴于原始资料年代久远、部分指标残缺，按《土工试验规程》（SD128-1984）划分。虽新近加固的堤身土体在土质及压实度方面进行了严格的控制，但其堤身土体的含水量及结构随季节变化仍会发生不同程度的改变，这是导致堤顶硬化道路开裂、堤身裂缝甚至临背河堤坡失稳变形的主要原因。

1.2数据收集

本研究收集了黄河下游堤防土样的实测资料（见表1），土样信息主要包括位置、干密度、黏粒含量以及实测土水特征曲线，共计20个土样。土样分布在黄河下游不同河段，土的分类涵盖了黏土、壤土、极细砂等主要堤身土质，干密度为1.3～1.7g/cm3。

1～18号土样数据来自同一出处，主要量测内容为不同基质吸力对应的脱湿及吸湿过程的土样含水量，测定方法为压力仪法。本文为方便区别不同吸力段实测值，将基质吸力范围为50～1500kPa的组次称为中吸力段，2～1000kPa的组次称为中低吸力段。

19、20号土样数据来自不同的文献资料，数据集内容主要为不同围压条件下的脱湿土水特征曲线，两者均为非饱和土三轴仪测定结果。19号土样的围压分别为0、100、200、300 kPa，基质吸力范围为0～80kPa;20号土样的围压分别为50、100、200、300、400kPa，基质吸力范围为0.1～50 kPa。

2土水特征曲线与黏粒含量关系探讨

2.1脱湿曲线特征

影响土水特征曲线的因素主要包括土的矿物成分、颗粒级配、干密度、收缩性、应力以及温度等。除矿物成分的影响外，其他因素均通过孔径来影响土水特征曲线，最终反映在曲线的形状上。经研究，黄河干支流的非黏土矿物组成基本相同，黏性土矿物组成也基本相同。本文主要聚焦于孔径的影响，考虑到颗粒级配是影响孔径的重要因素且测量手段简单快捷，因此基于颗粒级配尤其是黏粒的含量进行脱湿曲线的对比分析。

图1汇总了1～18号土样的脱湿曲线（中吸力段数据），根据黏粒含量以及脱湿曲线的不同大体将其分为4组，图中不同虚线表示各分组的模型拟合曲线（模型将在3.1节详细阐述），不同颜色的区域表示各分组模型拟合的80%预测带。

从图1中可以看出，黏粒含量越大，相同基质吸力对应的含水量越大，其原因是土样中黏粒越多，土体中的孔隙直径越小，对应的进气值以及残余含水量越大。4组土样的土水特征曲线位于明显不同的分区，但相邻组别土样分布区域有所重叠。18个土样的干密度范围为1.3～1.5g/cm’，在图中未区分干密度的影响，推断区域重叠原因可能是不同干密度导致孔隙大小不同。此外，黏粒含量为1%的土样（极细砂）与其他3组土样的土水特征曲线显著不同，最直观的表现为极细砂区域位于其他土样之下，且脱湿速率明显较小，这说明极细砂相较于壤土和黏土的持水能力较弱。

2.2吸湿与脱湿过程

土水特征曲线除上述脱湿过程外，还包括土样浸湿过程的吸湿曲线。图2为黏土、壤土、极细砂3种不同土质类型（黏粒含量不同）的中低吸力段脱湿及吸湿过程的土水特征曲线。可以看出：一方面，对于3种不同土类来说，曲线形状明显不同，随着黏粒含量的增大，其孔隙直径逐渐减小，相应的进气值增大，在同样含水量下的吸力逐渐增大，残余含水量也增大，且曲线斜率逐渐变小，脱水速率减小；另一方面，对于同一个土样来说，同一吸力时的脱湿含水量总是大于吸湿含水量，形成了明显的“滞回圈”。引起滞回效应的原因较为复杂，如孔隙尺寸均匀程度、孔隙几何形状、接触角大小等。在脱湿过程中要求气体通过颗粒间最细小的孔隙，水分的排出由小孔径孔隙所决定，而吸水过程中大孔径孔隙占主导地位，反映在图2中，即黏粒含量最大的粉质黏土孔隙大小差别最大，其滞回效应最明显：相比而言，黏粒含量最小的极细砂土体颗粒间孔隙最大且孔隙大小均匀，脱湿及吸湿曲线几乎重合，滞回效应最弱。

3与黏粒含量相关的土水特征曲线模型

3.1模型提出

目前有非常多的土水特征曲线模型，且不同模型存在不同的适用条件，模型参数大多与进气值、孔隙分布、残余含水量以及曲线斜率有关，如常用的Gardner模型、Van Genuchten模型以及FX模型等。以上模型所需参数较多，当量测基质吸力点数较少时，无法实现曲线拟合，给汛期黄河下游堤防安全的实时预报预警带来不便。近年来，有关学者通过压汞试验以及核磁共振等测量，证明了土体进气值、残余含水量与土体孔隙分布有较强对应关系。梳理有关研究成果发现，黄河下游堤防土样的土水特征曲线因黏粒含量不同而表现出明显的区别，考虑到不同干密度的土体孔隙大小不同，本文提出如下简易模型来预测黄河下游堤防非饱和土中吸力段土水特征曲线：

为验证本文模型适用性，利用Gardner模型拟合结果进行对比。表2为Gardner模型与本文模型在不同吸力段范围内的拟合结果统计，中吸力段因实测点较少、Gardner模型无法实现拟合计算，故其在表中无对应数据。经统计可看出：对于实测点较多的中低吸力段，Gardner模型及本文模型均可达到拟合优度R2>0.94的拟合精度：而当实测点数较少时，Gardner模型无法拟合并预测中吸力段土水特征曲线，本文模型可在一定程度上弥补这方面的不足。值得注意的是，本文模型对于极细砂的拟合精度普遍较其他类型土样的拟合精度低，原因可能是极细砂中的孔隙分布与黏粒含量较大的土样孔隙分布有明显区别。相比于脱湿曲线，本文模型对吸湿曲线的拟合精度较低，其原因是干燥脱水过程曲线由小直径孔隙决定，而在吸水过程中大直径孔隙占优势地位，小孔隙与黏粒含量相关度较高，大孔隙则与土体大颗粒含量、土体结构关系更密切，仅考虑黏粒含量不足以描述大孔径的分布特征。

3.2模型参数

图3为本文模型对1～18号土样脱湿过程中吸力段拟合所得参数a、6与m（m=np）之间的定量关系，参数a和参数b与m成线性关系，其中参数a为正相关，参数b为负相关。对于黏粒含量较小的极细砂（n=1%），参数a、b与m的关系点据严重偏离了其他土类的关系点据。此外，黏粒含量较小的轻壤土和轻粉质壤土（n=11%）以及砂质含量较大的砂质黏土也影响参数a的取值。

图4为1～18号土样吸湿过程中吸力段拟合结果，与脱湿曲线相同的是除极细砂以外，其他土样参数6与m成较好的负相关关系，且曲线斜率差别不大，而参数a则尚未发现与m有显著相关关系。图3、图4进一步印证了3.1节中提到的极细砂中孔隙分布与壤土、黏土孔隙分布有明显区别，且仅考虑黏粒含量及干密度因素不足以描述大孔径的分布特征，从而导致预测土水特征曲线脱湿过程的精度相对较低。

基于上述模型拟合参数a、b与黏粒含量n及干密度p之间的关系，在未来实际应用过程中，可在已知黄河下游堤防土体常规监测结果的基础上，预测中吸力段的土水特征曲线，在大幅降低直接测量时间成本的同时，为堤防洪水防御提供量化的支撑建议。如通过土水特征曲线、饱和渗透系数等基本特征参数，利用模型计算出堤防背水面的渗透量、滑塌临界时间等，为抢险救灾、确定居民安迁时机和规模提供建议。

4不同围压下的土水特征曲线预测

上文已明确参数a、b为黏粒含量n及干密度p的函数，为进一步贴近黄河下游堤防的受力情况，本节研究围压对土水特征曲线的影响，本文模型中引人参数c．具体模型形式如下：

利用该模型对19号土样在不同围压下的脱湿曲线实测值进行拟合，结果如图5所示。模型拟合优度R2均超过0.97，虽数据点数量较少，R2不能作为判定模型精度的唯一标准，但在一定程度上可以反映不同围压下的脱湿曲线特征。

从图5可以看出：随着围压a的增大，相同含水量对应的基质吸力逐渐增大。目前，有关学者认为围压并非直接影响土水特征曲线，而是通过改变土体干密度或孔隙状态来影响非饱和土的持水特征。但是，对于黄河堤防来说，往往需要关注不同偎堤水流速度、水深以及堤防在不同荷载条件下的持水特征，而这些因素将随着洪水过程及调度措施不断变化，采用实测孔隙度作为预测的因变量，将大大增加预测的物资及时间成本。目前应用于治黄实践的黄河下游水沙数学模型或水库联合调度模型可根据不同调度方案计算出偎堤水深、流速的变化，进而获得作用在堤防上的应力变化。在实际应用过程中，便可根据土样的常规监测结果以及堤防应力变化，通过以上简易模型预测堤防在汛期的土水特征曲线，为汛期堤防的安全评价提供基础参数。因此，虽然应力并不是影响土水特征曲线的直接因素，但是在黄河防汛支撑研究中，使用原始土体的颗粒级配、干密度以及应力变化作为因变量的模型则更具便捷性和时效性。

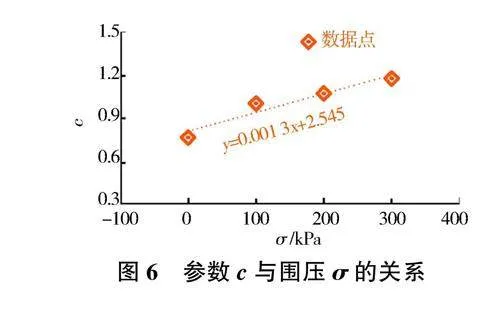
为进一步明确参数c与围压a之间的函数关系，将拟合参数c与围压a的关系点绘在图6中，结果表明随着围压的增大，参数c也增大。

同样，将20号土样在不同围压下的脱湿曲线实测值进行拟合。土样数据中尚未给定黏粒含量，可根据土质类型为粉质黏土（黏粒含量为30%～50%），分别假定n=30%、40%、50%为条件以及上文中参数a、6与m之间的函数关系，对20号土样进行拟合，结果如图7所示（以n=30%为例），拟合优度平均值为0.90。使用同样的方法，分别得出当黏粒含量分别为40%、50%时的参数c，与19号土样相同的是参数c随围压a的增大呈增大趋势。此外，结合19号土样及20号土样的拟合结果，当黏粒含量分别为17%、30%、40%、50%时，参数c与围压a的关系曲线斜率分别为0.0013、0.0014、0.0018、0.0023，由此可以推断，随着黏粒含量的增大，参数c随围压增大的速率也增大。本文初步探讨了模型中参数c的变化规律，但其具体的函数表达形式还需进一步的数据及理论支撑。

5结论

1）黄河下游堤防土体的土水特征曲线随黏粒含量的不同呈现出不同的特点，脱湿曲线可根据黏粒含量分为不同的区域，黏粒含量越大，相同含水量对应的基质吸力越大，相应的进气值越大，残余含水量越大，脱水速率越小，滞回效应越显著。

2）本文提出的与黏粒含量相关的土水特征曲线模型，对于黏粒含量为20%以上的壤土及黏土的脱湿曲线的适用性较好，可满足黄河下游堤防绝大多数土样类型的SWCC预测。

3）随着围压的增大，黄河下游堤防非饱和土相同含水量对应的基质吸力逐渐增大。本文模型引入与围压成正相关关系的参数c，可实现不同荷载下的土水特征曲线预测，在一定程度上满足了为汛期黄河防汛调度及时提供决策支撑建议的需要。