无线电测向运动的训练方法

〔摘 要〕 无线电测向运动作为科技体育运动，是逐渐从实际应用及军事中分离出来形成的运动，其集体育、科技于一体，深得学生喜欢。本文主要研究怎样结合小学生特点，进行无线电测向运动训练，通过对比，找到高效、实用、行之有效的训练方法，即运用概率与数理统计的方法分析平时训练数据，运用数学期望E（X）统计日常训练数据，由此反映每个学生在日常训练中的大致水平，并引入方差D（X）到成绩统计中，测算学生在日常训练中的成绩稳定性。

〔关键词〕 无线电测向；运动项目；训练方法

〔中图分类号〕 G424 〔文献标识码〕 A 〔文章编号〕 1674-6317 （2024） 22 097-099

在平时训练中，我们发现由于受各种因素的影响，学生的成绩起伏较大，这导致教练员不能系统地把握学生的训练情况，不能对症下药，有针对性地改善训练计划，从而影响训练效果。故而引入概率论与数理统计中的数学期望来统计学生的训练成绩，从而实现全面了解学生水平的目的。

一、引入数学期望E（X）判断学生的训练水平

运用概率与数理统计的方法分析平时训练数据，运用数学期望E（X）统计出学生的日常训练数据，它是简单算术平均的一种推广，类似加权平均，通过对数学期望的计算，可以反映出每个学生在日常训练中的大致水平。在日常训练中，受各种主观及客观条件的制约，即使是同一位学生的训练成绩有时也有很大的差异性。尤其是刚开始接触无线电测向运动训练的新成员，成绩忽好忽差、忽高忽低，让教师很难了解学生的水平。引入数学期望E（X）可以快速地了解学生的总体情况。

在实际中，由于测向运动是在规定时间让学生用测向设备找到规定的电台，小学阶段找台数为4个，且按规定顺序不能有误。所以具体操作如下：

为了方便计算，以每个学生的10次训练结果为一组，统计出学生10次训练中分别准确找到0个电台、1个电台、2个电台、3个电台和4个电台的概率，分别与0，1，2，3，4相乘后相加，即为每个学生在这10次训练中的数学期望。之所以将训练次数定为10次，是因为这样能较方便地统计出学生找出正确的电台的概率，方便计算数学期望值，这个数据反映了学生的10次训练的综合水平。现在引入计算数学期望E（x）的方法可以将学生的成绩量化，从而方便比较学生之间的差异，更好地改进训练方法。

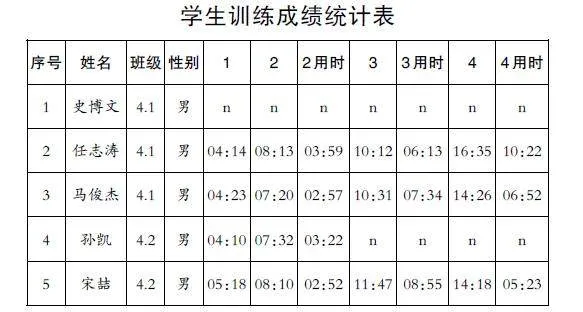
由于小学阶段学生找台数规定为4个，且按规定顺序不能有误，所以，要先计算出学生找台的准确率。如下表所示，这是一张学生平时训练的成绩统计表，每训练一次都会得到一张。

表中，n代表找错台，用时为null，即为空；数字1，2，3，4分别代表找到1号台，2号台，3号台，4号台所花费的时间，中间的“2用时，3用时，4用时”分别代表找到1号台到找到2号台的时间间隔，找到2号台到找到3号台的时间间隔，找到3号台到找到4号台的时间间隔。

但是单看这种成绩表，直观性很差，尤其是学生成绩起伏较大时，有时这次训练成绩很好，有时那次训练成绩很差，很难看出一位学生的整体水平。由此产生一个问题，如何利用这类成绩表，来反映一位学生一个阶段内的综合性水平。通过数学期望的引入，可以直观地了解学生的训练水平，具体计算方法如下。

将10张这样的成绩单进行统计，分别统计出每个学生找到0个电台、1个电台、2个电台、3个电台和4个电台的概率，以1号学生史博文为例，在10次训练中，他准确地找到1个台的次数为1次，准确找到2个台的次数为3次，准确找到3个台的次数为0次，准确找到4个台的次数为3次，1个台也没找到的次数为6次，所以他的找台率分别为：0.6，0.1，0.3，0，0（为方便起见，将一个台也没找到的概率放在最前面）；

同理2号学生任志涛在10次训练中，他准确地找到1个台的次数为2次，准确找到2个台的次数为5次，准确找到3个台的次数为2次，准确找到4个台的次数为1次，1个台也没找到的次数为0次，所以他的找台率分别为：0，0.2，0.5，0.2，0.1；

3号学生马俊杰在10次训练中，他准确地找到1个台的次数为1次，准确找到2个台的次数为3次，准确找到3个台的次数为3次，准确找到4个台的次数为3次，1个台也没找到的次数为0次，所以他的找台率分别为：0，0.1，0.3，0.3，0.3；

4号学生孙凯在10次训练中，他准确地找到1个台的次数为1次，准确找到2个台的次数为7次，准确找到3个台的次数为1次，准确找到4个台的次数为1次，1个台也没找到的次数为0次，所以他的找台率分别为：0，0.1，0.7，0.1，0.1；

5号学生宋喆在10次训练中，他准确地找到1个台的次数为2次，准确找到2个台的次数为3次，准确找到3个台的次数为5次，准确找到4个台的次数为0次，1&个台也没找到的次数为0次，所以他的找台率分别为：0，0.2，0.3，0.5，0。

以此类推，算出每个同学在10次训练中分别找到0个电台、1个电台、2个电台、3个电台和4个电台的概率。

然后将学生10次的训练结果总结统计出准确找到0个电台、1个电台、2个电台、3个电台和4个电台的概率，分别与0、1、2、3、4相乘后相加，即为每个学生在这10次训练中的数学期望值。具体计算方法如下：

在10次训练中分别找到0个电台、1个电台、2个电台、3个电台和4个电台的概率第一位学生史博文为0.6，0.1，0.3，0，0，分别与相对应的台数0，1，2，3，4相乘，则第一位学生史博文的数学期望E（x1）=0×0.6+1×0.1+2×0.3+3×0+4×0=0.7；

第二个学生任志涛的找台概率为0，0.2，0.5，0.2，0.1；分别与相对应的台数0，1，2，3，4相乘，则第二学生任志涛的数学期望E（x1）=0×0+1×0.2+2×0.5+3×0.2+4×0.1=2.2；

第三个学生马俊杰的找台概率为0，0.1，0.3，0.3，0.3；分别与相对应的台数0，1，2，3，4相乘，则第三个学生马俊杰的数学期望E（x1）=0×0+1×0.1+2×0.3+3×0.3+4×0.3=2.8；

第四个学生孙凯的找台概率为0，0.1，0.7，0.1，0.1；分别与相对应的台数0，1，2，3，4相乘，则第四个学生孙凯的数学期望E（x1）=0×0+1×0.1+2×0.7+3×0.1+4×0.1=2.2；

第五个学生宋喆的找台概率为0，0.2，0.3，0.5，0；分别与相对应的台数0，1，2，3，4相乘，则第五个学生宋喆的数学期望E（x1）=0×0+1×0.2+2×0.3+3×0.5+4×0=2.3。

以此类推，可以算出所有同学10次训练的数学期望。根据计算得知，前五个同学中，马俊杰数学期望最高，史博文数学期望值最低，对应相关成绩，马俊杰找到4个台的概率也是五人中最高的。查看后面的数据就会发现，有的同学找到4个台的概率没有马俊杰高，但其数学期望却要高于马俊杰的2.8，这是因为数学期望算的是一种均值，对应到训练中，算的是一个阶段内学生的平均成绩。根据数学期望，可以看出学生在此阶段内的大致水平，并以此为依据，及时调整训练计划。

同时，我们也发现了存在的其他问题。在数学期望值一样的情况下，如何分析学生的训练成绩。二号同学任志涛和四号同学孙凯的数学期望值都是2.2，但他们的找台概率明显不同。怎样区分这里的同学的能力水平呢？

二、引入方差D（X）判断学生的训练成绩

在平时训练中，由于学生成绩波动较大，很难判断两个学生谁的成绩稳定一些，尤其当两个学生水平接近的情况下。在这种情况下可以引入方差的概念加以判断。方差是在概率论和统计方差衡量随机变量或一组数据时离散程度的度量。概率论中方差用来度量随机变量和其数学期望（即均值）之间的偏离程度。现引入成绩统计中，可以测算学生在日常训练中的成绩稳定性。离散型方差的计算式为：D（X）=<E：＼小学科学2024-22期361＼Image＼image2.pdf>，其中μ=E（X）。由于这个公式计算起来比较麻烦，我们采用随机变量方差的化简公式D（X）=E（X2）-[E（X）]2。因此计算方差的方法为先将数学期望中的0，1，2，3，4替换成他们的平方，即0，1，4，9，16再与对应的概率相乘计算出数学期望，然后与已经计算的数学期望的平方相减就得到对应的方差（方差无负值）。如第一位学生史博文的找台概率为0.6，0.1，0.3，0，0，分别与相对应的台数的平方0，1，4，9，16相乘，再与他的数学期望0.7的平方相减，则第一位学生史博文的数学期望D（X1）=（0×0.6+1×0.1+4×0.3+9×0+16×0）-0.5=0.8；

第二个学生任志涛的找台概率为0，0.2，0.5，0.2，0.1；分别与相对应的台数的平方0，1，4，9，16相乘，再与他的数学期望2.2的平方相减，则第二个学生任志涛的数学期望D（X2）=（0×0+1×0.2+4×0.5+9×0.2+16×0.1）-4.8=0.8；

第三个学生马俊杰的找台概率为0，0.1，0.3，0.3，0.3；分别与相对应的台数的平方0，1，4，9，16相乘，再与他的数学期望2.8的平方相减，则第三个学生马俊杰的数学期望D（X3）=（0×0+1×0.1+4×0.3+9×0.3+16×0.3）-7.8=1；

第四个学生孙凯的找台概率为0，0.1，0.7，0.1，0.1；分别与相对应的台数的平方0，1，4，9，16相乘，再与他的数学期望2.2的平方相减，则第四个学生孙凯的数学期望D（X4）=（0×0+1×0.1+4×0.7+9×0.1+16×0.1）-4.8=0.6；

第五个学生宋喆的找台概率为0，0.2，0.3，0.5，0；分别与相对应的台数的平方0，1，4，9，16相乘，再与他的数学期望2.3的平方相减，则第五个学生宋喆的数学期望D（X5）=（0×0+1×0.2+4×0.3+9×0.5+16×0）-5.3=0.6。

因为方差越小越稳定，表示数据间差别小，稳定性高。所以虽然第二个学生任志涛的数学期望和第四个学生孙凯相等，但是根据方差计算结果，第四个学生孙凯的成绩要比第二个学生任志涛稳定得多；这是对学生成绩的一个重要参考，尤其是在比赛选拔过程中学生成绩相近的情况下。先利用数学期望进行排序，再根据方差进行进一步的判断。

综上所述，利用数学期望要结合方差进行才能达到好的效果，只看其中一项是不全面的。因为只从数学期望分析，看到的只是学生一个阶段成绩的平均情况，而许多学生平时训练时成绩很不稳定，只看平均值并不能全面了解学生的真实水平。而方差只代表稳定性，有的学生十分稳定，但是在训练成绩止步不前的基础上，这样的稳定只能说明此类学生的训练计划需要调整，并不代表学生的水平提高。只有将这两种数据结合起来，才能比较全面地了解一位学生的一个阶段内的训练结果。

三、训练存在的问题与研究设想

（一）存在的问题

方差只注重稳定性，但过于稳定说明学生没有进步，不稳定又很难判断学生成绩是上升了还是下降了，所以只能在一定条件下结合其他成绩参考使用，在比赛前选拔运动员时作为一项重要指标，平时限制较大。本课题只对测向运动中学生找台过程中的准确率进行了研究，在如何缩短找台时间上并未太多涉及，只侧重于训练的一个方面，并没有全面的研究。

（二）研究设想

数学期望注重于平均值，方差的统计只注重稳定性，在细化研究时都有局限性。今后在此基础上结合找台率进行学生的精细化个性化研究。本次课题主要研究为提高学生有效性训练，引入数学期望及方差对学生成绩进行统计，可以快速、高效地了解学生的训练成绩及稳定性，今后可以将学生的找台时间加入统计计算的范畴，探索新的加权方式，将找台准确率与找台时间有机统一起来，进行更加完整的研究。

参考文献

[1]中华人民共和国教育部.关于加强和改进中小学实验教学的意见[S]北京：教基〔2019〕16号，2019.11.

[2]肖继先.概率论与数理统计[M].北京：科学出版社，2012.