Polypad工具在数学教学中的应用

摘要：本文介绍了一款实用工具——Polypad，并通过教学片段分析和总结了该工具在数学教学中的应用，希望通过合理运用能够提高学生学习数学的主动性。

关键词：实用工具；Polypad；教学片段

中图分类号：G434 文献标识码：A 论文编号：1674-2117（2024）19-0093-03

教学片段一：利用Polypad进行平面镶嵌活动

《义务教育数学课程标准（2022年版）》提出：“初中阶段综合与实践领域，可采用项目式学习的方式，以问题解决为导向，整合数学与其他学科的知识和思想方法，让学生从数学的角度观察与分析问题、思考与表达、解决与阐释社会生活以及科学技术中遇到的现实问题，感受数学与科学、技术、经济、金融、地理、艺术等学科领域的融合，积累数学活动经验，体会数学的科学价值，提高发现与提出问题、分析与解决问题的能力，发展应用意识、创新意识和实践能力。”“实践性”是综合与实践内容的基本特征之一，而单靠实践比较耗时、费力，此时若适当借助数字资源辅助教学，则会收到意想不到的效果。下面，笔者以七巧板为例介绍如何设计瓷砖进行平面镶嵌。具体操作步骤如下：

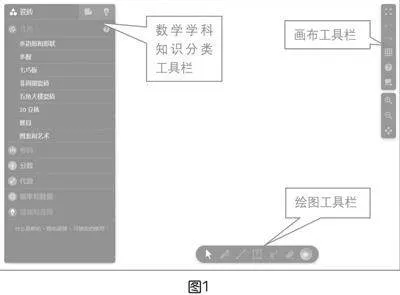
（1）进入Polypad操作界面（如图1），界面共分三个工具栏，左侧工具栏中有几何、代数和概率等大量实用工具，界面的空白处是画布区域。

（2）在Polypad界面左侧工具栏中打开“几何”下的“多边形和形状”，这里提供了一些常用的多边形，把一个正方形拖入到画布中，选中正方形后在图形下方会弹出一个工具框，选择“切”工具，把正方形切成两半。

（3）按照相同的方法，把正方形切成七部分，然后分别设置成不同的颜色进行区别，最后把它们分散排列开来，这样就制作好了一个七巧板，如下页图2所示。学生利用自己制作的七巧板就可以进行镶嵌活动了。

教学片段二：利用Polypad探寻杨辉三角规律

在数学学习中，学生经常需要通过观察来探究规律。“杨辉三角”是人教版八年级上册“阅读与思考”栏目的内容，利用传统的教学方式，教师往往难以激发学生参与探究的积极性，因此可以借助Polypad画布，引导学生绘制庞大的“杨辉三角”，然后从不同角度观察、探究其中蕴涵的规律。具体操作步骤如下：

（1）在Polypad界面左侧工具栏中打开“号码”下的“号码卡”，把号码拖到画布中并排列成杨辉三角图形。需要注意的是，利用号码卡最后一栏中的输入框可以输入任意一个号码，如图3所示。

（2）引导学生探究杨辉三角中蕴涵的规律。先让学生全选一行数字，然后选择复制，接着选择合并（如图4），此时所复制的这一行数会自动合成一个数，如第4行的5个数会合成16，重复这样的操作，学生容易发现每一行各数之和刚好是行数的平方。接着，引导学生继续合作探究杨辉三角中蕴涵的其他规律。

（3）教师打开“数学游乐场”课程部分的课例资源——帕斯卡三角（杨辉三角），与学生共同欣赏杨辉三角的美，探索、总结杨辉三角中蕴涵的规律。这里的杨辉三角非常庞大、简洁，而且具有互动性。例如，可以通过不同的颜色，体现从不同角度看到不同的序列以及由这些序列形成的神奇的图案，如斐波那契数列等。

教学片段三：利用Polypad探究函数图像的规律

在初中阶段，学生主要学习的函数是一次函数、二次函数和反比例函数。以二次函数为例，学生用描点法画图，基本上能看出二次函数表达式中的系数与图像和对称轴的关系，但是若每次改变a、b、c的值都用描点法画图，是比较耗时、费力的，此时可引导学生在Polypad中绘制二次函数图像并通过改变a、b、c的值来探究图像的变化规律。具体操作步骤如下：

（1）在Polypad界面左侧工具栏中打开“代数”下的“坐标和表格”，把一个坐标轴拖到画布中，接着打开“代数”下的“可变滑块”，拖动“a、b、c”三个可变滑块到画布中。

（2）选中界面最下方绘图工具栏中的“x2”方程工具，在画布中输入方程“a·x2+b·x+c”，然后单击它，界面下方出现绘图图标（如下页图5），单击它，系统就会自动绘制出二次函数的图像，改变三个可变滑块，改变系数的值，函数图像也会随着改变。

教学片段四：利用Polypad探究完全平方公式

教科书中的几何图形是静止的，难以激发学生探究的热情，若让学生借助Polypad画布制作“代数瓷片”，构造几何图形，则可以大大提高学生参与课堂的积极性。

例如，学生在学习完全平方公式时往往会出现“（x+y）2=x2+y2”的错误，若能借助Polypad，通过对面积的讨论，学生便可以发现完全平方公式与面积之间的内在联系，从而更容易记住公式“（x+y）2=x2+2xy+y2”，进而感受到几何与代数内在的统一性。具体操作如下：

（1）在Polypad界面左侧工具栏中打开“代数”下的“代数瓷片”，依次将面积为x2、y2、xy的矩形拖到画布中，拼接成如图6所示图形。

（2）当Polypad界面左侧工具栏中没有现成的“代数瓷片”时，可以教学生自己制作瓷片，如要在Polypad画布中构造图形说明等式“（x+3）2=x2+6x+9”，可以操作如下：

①从Polypad界面左侧工具栏中拖动面积为x2的瓷片，然后点击画布下方工具栏中的“复制”按钮，复制三份备用。

②单击第1张备份瓷片，点击画布下方工具栏中的“水平分割”按钮，点击2次，便可将其平均分成4份，然后点击画布下方工具栏中的颜色按钮，将颜色设置为绿色，并在这些瓷片上标注“x”，拖动其中的3份，拼接到瓷片（x2）下方。类似地，单击第2张备份瓷片，点击画布下方工具栏中的“垂直分割”按钮，点击2次，便可将其平均分成4份，然后点击画布下方工具栏中的颜色按钮，将颜色设置为绿色，并在这些瓷片上标注“x”，拖动其中的3份，拼接到瓷片（x2）右方。

③单击第3张备份瓷片，先后点击画布下方工具栏中的“水平分割”和“垂直分割”按钮各2次，便可把这块瓷片平均分成16份，然后点击画布下方工具栏中的颜色按钮，将颜色设置为橙色，在这些瓷片上标注“1”，然后拖动其中的9份依次拼接到刚才所得图形的右下方，得到一个正方形，这个正方形可以直观表达等式“（x+3）2=x2+6x+9”。

（3）滑动Polypad界面左侧工具栏下方的“x滑条”，可调整画布中图形的大小。学生可以用类似的方法，在画布中构造不同的图形来表示不同的等式，如x2-4x+4=（x-2）2，x2+6x+2=（x+3）2-7等，学生在操作中得以从几何的角度直观地理解完全平方公式和“配方”，体会几何与代数内在的统一性，感悟数形结合思想。

限于篇幅，Polypad更多的应用有待大家自行探索。

基金项目：广西教育科学“十四五”规划2023年度课题“初中数学项目式学习的实践与研究”（编号：2023C402）。