基于水下双雷平行航向齐射模型的多参数自适应寻优方法研究

摘 要： 为提升水下目标捕获概率，双雷平行航向齐射方式得到广泛采用，而该齐射模型中打击提前角、展开系数、展开散角均对目标捕获概率产生影响，相关领域之前的研究主要聚焦双雷展开系数与展开散角对目标捕获概率的影响，存在一定局限性。针对双雷平行航向齐射射击方式，首先给出了一种提升双雷捕获概率的平行航向齐射模型，理论推导了模型中多参数最优解方程，给出了一种多参数自适应寻优方法用以求解方程;其次结合仿真实验，基于蒙特卡洛方法，通过对比双雷齐射传统模型与优化模型的目标捕获概率，验证了多参数自适应寻优方法的可行性。研究成果为进一步使用鱼雷齐射战术提供了有效参考。

关键词：平行航向齐射;自适应优化;打击提前角;展开系数;展开散角

中图分类号：TJ630 文献标志码：A DOI：10.3969/j.issn.1673-3819.2024.04.007

引用格式：

史旭峰，李谦，李彦，等.

基于水下双雷平行航向齐射模型的多参数自适应寻优方法研究

.指挥控制与仿真，2024，46（4）：53-59.

SHI X F，LI Q，LI Y，et al.

Study on multi parameters adaptive optimization based on double torpedoes salvo in parallel mode

.Command Control & Simulation，2024，46（4）：53-59.

Study on multi parameters adaptive optimization based on double torpedoes salvo in parallel mode

SHI Xufeng， LI Qian， LI Yan， XIA Qianxin

（The 705 Research Institute， China Shipbuilding Industry Corporation， Xian 710077， China）

Abstract：In order to improve the probability of underwater target capture， the double-mine parallel heading salvo method has been widely adopted， and the strike advance angle， deployment coefficient and spread angle of the salvo model all affect the target capture probability， and previous research in related fields mainly focuses on the influence of double mine deployment coefficient and spread scatter angle on target capture probability， which has certain limitations. In this paper， a parallel heading salvo model to improve the probability of double mine capture is given， and a multi-parameter optimal solution equation is theoretically derived， and a multi-parameter adaptive optimization method is given to solve the equation. Combined with simulation experiments， based on Monte Carlo method， the feasibility of multi-parameter adaptive optimization method is verified by comparing the target capture probability of the traditional double-ray salvo model with the optimization model. The results of the study provide an effective reference for the further use of torpedo salvo tactics.

Key words：torpedoes salvo in parallel course mode; adaptive optimization method; strike advance angle; spread coefficient; spread dispersion angle

收稿日期： 2023-06-12

修回日期： 2023-06-29

作者简介：

史旭峰（1990—），男，硕士，工程师，研究方向为水下攻防体系研究。

李 谦（1992—），男，博士，工程师。

随着我国海军军事实力不断提升，水面舰艇编队日趋庞大，现代海战中，敌方潜艇作为水下主要武器，仍对水面舰艇编队安全产生重要威胁，这就要求水面舰艇必须充分发挥其携带反潜武器的作战效能，提升对水下目标的捕获概率。

受限于分辨率和建设成本，当前的侦察星座难以实现对目标的连续侦察，星座建设效果通常受重访时间、响应时间、覆盖持续时间、覆盖时间及建设成本等多方面影响。这些指标间存在诸多冲突，无法同时达到最优状态，需要设计者进行折中权衡，这是一种典型的多目标优化问题。

近年来，针对星座多目标优化问题，研究者们已设计出多种星座优化方案。文献[1]提出一种分层染色体编码方法，在不限制特定几何形状的情况下，对不同大小的星座进行编码，该方法能快速生成数量充足的观测卫星星座，在保证时效性的同时提供最大的覆盖性能；文献[2]对标准PSO（Particle Swarm Optimization，粒子群）算法的收敛速度和全局搜索能力做出了改进，设计优化了高时间分辨率全球覆盖和区域覆盖遥感卫星星座；文献[3]利用免疫算法设计每天重访次数不小于规定值的侦察星座；文献[4]利用基于精英优化选择策略的动态多目标差分进化算法对星座进行优化。上述方案在对侦察卫星星座进行优化时所采用目标维数不足3项。随着技术的发展，航天侦察在情报侦察中所占比重的上升，研究人员需要对侦察星座的多个指标进行优化，由于目标维数往往较大，侦察星座优化逐渐演变为一个高维多目标优化问题。在此情况下，传统的进化算法会出现选择压力丧失，多样性无法维护等问题，优化效果较差[5]。

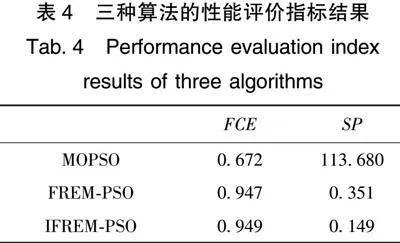
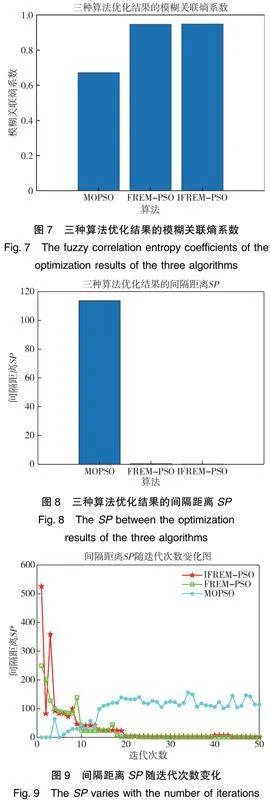
本文在建立侦察卫星星座优化指标体系基础上，建立五目标优化的侦察星座优化模型，并提出改进的基于模糊关联熵的粒子群算法（Improved Particle Swarm Optimization Algorithm Based on Relative Entropy of Fuzzy Sets， IFREM-PSO）[6]。该算法利用模糊关联熵系数对种群中的个体进行排序，改进自适应惯性权重策略及外部档案维护策略提高收敛速度、收敛精度与多样性。该算法引入变异策略，避免陷入局部最优解。研究人员采用IFREM-PSO算法对面向区域目标的成像侦察星座进行优化，以更好地解决侦察星座的高维多目标优化问题。

1 侦察星座优化模型

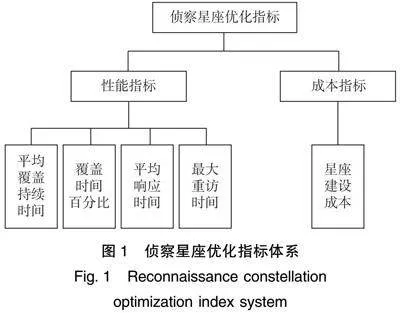
研究人员设计面向区域的成像侦察星座需要考虑到星座的最大重访时间、平均覆盖持续时间和平均响应时间，以实现对目标接近实时的侦察，便于判断目标的运动态势。目标的运动特性和出现位置的不确定性对星座覆盖时间百分比提出了更高要求。卫星的造价与发射成本高昂，因此，研究人员需要在满足性能指标要求前提下，尽可能节约成本。综上，研究人员选择平均覆盖持续时间、覆盖时间百分比、平均响应时间、最大重访时间和星座建设成本作为侦察星座的优化目标，并建立侦察星座的优化指标体系如图1所示。

侦察星座的优化模型包括目标函数与决策变量两方面。

1.1 目标函数

研究人员将平均覆盖持续时间、覆盖时间百分比、平均响应时间、最大重访时间和星座建设成本作为优化指标。其中，平均覆盖持续时间、覆盖时间百分比、平均响应时间和最大重访时间需要通过计算星座中的每颗卫星对目标区域的覆盖情况得出。

侦察卫星星座拓扑结构不断变化，星座覆盖区域亦动态变化，同时，侦察星座对区域的覆盖具有非对称性[7]。这些因素导致很难通过解析方法对星座的覆盖性能进行求解。目前求解星座覆盖性能主要采用网格点法[8]，即以一定经纬度间隔对地表区域进行网格划分，将落在目标区域内的网格点作为特征点，利用目标区域内所有样本点的平均覆盖特性来代表整个目标区域的覆盖特性，从而将星座对地覆盖情况进行简化。

平均覆盖持续时间f1表示在一次侦察任务中，目标区域平均每次被覆盖到的时间。平均覆盖持续时间f1可表示为

f1=1M∑M∑Nm（tenm-tsnm）Nm（1）

其中，M为网格点的个数，Nm为在整个侦察持续时间内对点m的访问次数，tsnm为对网格点m的第n次访问的开始时间，tenm为对网格点m的第n次访问的结束时间。

覆盖时间百分比f2为目标区域至少被星座中一颗卫星覆盖的时间占整个侦察任务总时间的百分比，反映星座的利用效率。覆盖时间百分比越大说明星座中卫星的利用率越高。则网格点m的覆盖时间百分比f2（m）可表示为

f2（m）=∑Nm（tenm-tsnm）T（2）

其中，T为侦察任务总时间。

平均响应时间f3是指整个侦察持续时间中，从对某一个点提出侦察请求到开始侦察该点所经历时间T的平均值。平均响应时间f3可表示为

f3=1M∑M∑Nm（tsn+1m-tenm）22Nm（3）

其中，tsn+1m为对网格点m的第n+1次访问的开始时间。

最大重访时间f4是指星座连续两次开始访问某一目标的时间间隔的最大值。这个指标反映星座的连续覆盖能力以及星座对地覆盖的最差情况，最大重访时间值越小表示星座连续对地覆盖的能力越强。最大重访时间f4可表示为

f4=max{（tsn+1m-tsnm）|m∈［1，M］，n∈［1，Nm-1］}（4）

星座建设成本f5分为生产成本和发射成本。生产成本主要由星座中的卫星总数决定；发射成本的计算主要影响因素为星座轨道面数量、每个轨道面内卫星数、卫星轨道高度和轨道倾角。星座建设成本f5采用文献[5]所定义的公式。

根据选取指标建立多目标优化模型，模型的数学表示如下：

min F（x）=min（-f1（x），-f2（x），f3（x），f4（x），f5（x））（5）

gi（x）<0，i=1，2，…，k（6）

hi（x）=0，i=1，2，…，l（7）

其中，x=（x1，x2，…，xv）为决策向量，它在决策空间内，fi（x）为指标i的目标函数，gi（x）为不等式约束，hi（x）为等式约束。

1.2 决策变量

侦察星座是由一组人造侦察卫星为了获取情报信息而协同工作组成的系统[9]。侦察星座的性能主要受星座构型和卫星轨道影响[10]。当前主流的星座构型包括Walker星座、Flower星座、共地面轨迹星座和太阳同步轨道星座。Walker星座空间分布均匀，覆盖性能较好，适合于对全球进行侦察，经过设计的Flower星座和共地面轨迹星座对某个特定区域的覆盖性能可以达到最优[11]，太阳同步轨道星座可以提供独特的可见光观察特性，适合光学成像卫星进行侦察，但覆盖性能欠佳。

可见光成像侦察分辨率高，易于判读[12]，是当前进行航天侦察的主要手段。因此，本研究采用可见光成像卫星对目标区域进行侦察。考虑我国周边所需关注的区域分布较为广阔，因此采用具有良好的均匀覆盖特性的Walker星座，便于实现对所有关注区域的均匀覆盖。Walker星座的示意图如图2所示。

Walker星座是一个圆轨道星座，在Walker星座中，每颗卫星都具有相同的轨道高度、轨道倾角和偏心率，Walker星座由轨道面数P、每个轨道面内卫星数S和相位因子F决定。由于侦察星座工作持续时间长cd5dbc59a2294b4ad63e49b51c9b5d30ca0f3b4e7dbef1396696e9d4abdf5c89达数年，相位因子F对于星座的影响可忽略不计。因此，选择轨道面数P、每个轨道面内卫星数S作为决策变量。

卫星轨道确定参数包括轨道高度h、轨道倾角inc、偏心率e、升交点赤经Ω、近地点辐角ω和真近点角υ。由于升交点赤经Ω、近地点辐角ω和真近点角υ对需要优化的目标影响较小，选择轨道高度h和轨道倾角inc作为决策变量。

综上，采用轨道面数P、每个轨道面所含卫星数S、轨道高度h和轨道倾角inc作为模型的决策变量。根据已有理论和先验知识，将它们的含义和变化范围如表1所示。

2 基于模糊关联熵的粒子群算法

传统的进化算法多采用Pareto支配对算法中的个体进行排序，这种支配方式只适合目标维数低于3的多目标优化问题，在对侦察星座进行高维多目标优化时，传统的基于Pareto支配的进化算法会出现选择压力不足，难以对种群中个体的优劣做出区分的问题。为了增强算法的收敛性，实现对侦察星座更好的优化，本文引入了FREM-PSO算法，并对算法的自适应惯性权重与外部档案维护策略进行改进，增强算法的收敛速度、收敛精度和多样性，引入变异策略，避免算法陷入局部最优解。本文提出的IFREM-PSO算法流程如图3所示，概述如下：

Step1：分别对每个子目标进行单目标优化，得到每个子目标的最优值和最劣值；

Step2：分别对子目标的最优值和最劣值进行处理，得到fbi和fwi，将每个子目标的fbi组合，建立理想解fb1，fb2，fb3，fb4，fb5，之后，对其进行隶属度映射；

Step3：令迭代次数t=0，随机生成初始化种群并对种群中所有粒子进行隶属度映射，之后，将FCE最大的个体设为种群最优个体gb0，将当前得到的初始化种群设为初始的外部档案Archive0和个体历史最优解pb0；

Step4：更新每个粒子的自适应惯性权重wi与速度vt，之后根据上一次迭代的位置xt-1与本次迭代的速度vt计算得到位置x*；

Step5：生成变异位置x′；

Step6：对于每一个粒子，在位置x*与变异位置x′中，选择FCE更大的一个作为临时位置xt；

Step7：对于每一个粒子，在临时位置xt与上一次迭代产生的位置xt中，选择FCE更大的一个作为本次迭代生成的位置xt，对种群中所有粒子均执行此操作，直到所有粒子均得到迭代后的位置xt；

Step8：将本次迭代完成后生成的新种群Populationt与原外部档案Archivet-1合并；

Step9：在合并后的种群中，根据外部档案维护策略选择出新的外部档案Archivet；

Step10：令迭代次数t加1，若当前迭代次数达到规定的最大迭代次数N，则停止迭代，输出外部档案Archivet+1中存储的粒子作为最终解集；否则，进入Step4。

2.1 PSO算法

PSO算法是一种模拟鸟类群体社会行为的智能搜索算法，算法易于实现，参数空间小，搜索效率高[13]，收敛速度快，是当前被广泛应用的一种优化算法。

PSO算法实现简单，参数较少，研究人员在使用PSO算法时，只需确定种群数量pop、迭代次数N、目标函数维度M、决策变量维度V、学习因子c1和c2、惯性系数w即可。其中，种群数量pop即为PSO算法中包含的粒子个数，由使用者希望获得的最优解集中解的个数决定；迭代次数N代表算法经过N次位置更新，得到最终结果；目标函数维度M由优化的子目标个数决定；决策变量维度V由决策变量个数决定；学习因子c1和c2与惯性系数w是在进行速度更新时用于平衡速度大小、帮助粒子更好地找到最优解的参数，可根据经验进行设置。

由于多目标优化问题不存在一个令所有优化目标都达到最优的解，只能找到一个在各目标之间折中调和后的最优解集，在使用优化算法进行求解时，通常使用一个种群对问题的解进行搜索，从而保证优化结果能够为使用者提供多样化的解决方案。在PSO算法中，种群包含pop个粒子，每个粒子代表一个解决方案。粒子具有两种属性：位置和速度。位置代表当前的决策变量方案，速度决定下一步搜索的方向与步长。每经过一次迭代，粒子的位置与速度都会进行更新，第t+1次迭代时，粒子的速度vt+1i由粒子上一次迭代的速度vti、当前的种群历史最优粒子gbt、当前的粒子历史最优位置pbti以及粒子第t次迭代所生成的位置xti决定，对于编号为i的粒子，它在第t+1次迭代时的速度vt+1i计算方式如下：

vt+1i=wi*vti+c1*r1*（pbti-xti）+c2*r2*（gbt-xti）（8）

其中，wi为粒子i的惯性系数，c1、c2为学习因子，r1、r2为两个随机数。

粒子i第t+1次迭代完成后所处的位置xt+1i由该粒子上一次迭代所生成的位置xti与本次迭代的速度vt+1i决定：

xt+1i=xti+vt+1i（9）

2.2 自适应惯性权重

在粒子群算法中，速度用于调整粒子的搜索方向与步长，而惯性权重是影响速度大小的一个重要因素。在FREM-PSO算法中，惯性权重采用了根据迭代次数自适应变化的策略，认为搜索会随着迭代次数逐步向Pareto前沿靠近，因此，令惯性权重随迭代次数的增长逐渐减小。这种方法对于搜索精度有一定改善，但迭代次数无法准确反映当前粒子与Pareto前沿之间的收敛程度。

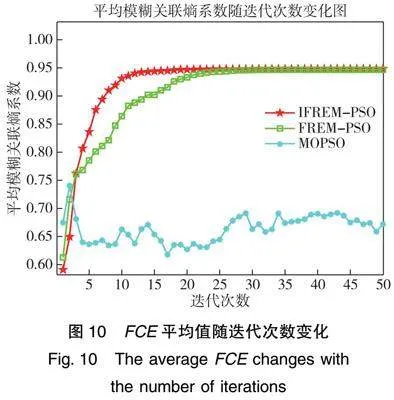
基于此，本文提出基于模糊关联熵系数的自适应惯性权重，令惯性权重的取值与模糊关联熵系数成负相关。当模糊关联熵系数在0附近时，认为当前解与真实Pareto前沿距离较远，令惯性权重尽可能大，并随模糊关联熵系数变化缓慢，从而帮助种群尽快摆脱质量不佳的搜索空间，加快向真实Pareto前沿收敛；当模糊关联熵系数接近1时，认为此时粒子在真实Pareto前沿附近，减小惯性权重取值，使搜索步长减小，从而更精确地逼近真实Pareto前沿。令自适应惯性权重策略如下式所示：

wi=（wini-wend）*（1-e3（1-1FCEi）-1）+wini（10）

其中，wi为粒子i当前惯性权重，wini和wend分别为惯性权重的上限和下限，FCEi（Fuzzy Correlation Entropy Coefficient， 模糊关联熵系数）为粒子i对应的模糊关联熵系数。改进的自适应惯性权重随FCEi变化的曲线如图4所示。

2.3 变异策略

由于FREM-PSO是在粒子群算法的基础上进行的改进，算法存在容易陷入局部最优解的情况[14]。为帮助算法摆脱局部最优解，算法在迭代过程中引入变异策略。种群中的粒子在受速度vt影响生成位置x*的同时，按照概率p生成一个变异个体x′，之后，通过比较x*与x′之间的FCE值确定粒子的临时位置xt，从而为算法提供更多进化方向，并引导种群向更好的方向收敛，避免陷入局部最优。变异策略的流程如图5所示。

自适应变异概率p计算方式为

p=1-（t-1N-1）1μ（11）

其中，t为当前迭代代数，N为迭代总代数，μ为变异系数，其值设为0.1。

2.4 适应度函数计算

适应度函数是评价种群中粒子优劣的关键依据，决定了算法运行速度的快慢以及能否收敛到真实Pareto前沿。算法采用隶属度映射后的当前解与理想解之间的模糊关联熵系数作为算法的适应度函数。

模糊关联熵是衡量两个模糊集之间相似程度的一种度量，模糊关联熵系数是由模糊关联熵导出的，刻画两个模糊集之间相似程度的度量[13]。两个模糊集之间相似度越高，模糊关联熵系数越大。因此，研究人员将理想模糊集作为评价标准，就可以通过计算其他模糊集与理想模糊集之间的模糊关联熵系数来判断其他模糊集之间的优劣。

多目标优化问题中每个子目标都存在一个最优解，研究人员将每个子目标的最优解进行组合，就可以形成一个现实中无法达到的理想解。基于模糊关联熵的算法表明当前解与理想解之间相似程度越高，则当前解的质量越好，反之则认为越差。因此，本文可以通过计算当前解与理想解之间的相似程度区分当前解的优劣情况，进而引导算法选择更优的解进行进化。而隶属度映射可以将多目标解转化为隶属度模糊集，从而引入模糊关联熵的概念，对当前解和理想解之间的相似程度进行度量，引导种群进化。

综上，基于模糊关联熵的进化算法首先通过单目标优化算法分别求得每一个子目标的最优解和最劣解，并经过处理作为子目标的上下限，之后令所有子目标的最优解组合形成理想解，将当前解与理想解映射为模糊集，并计算两个模糊集之间的模糊关联熵系数，进而判断当前解与理想解之间的相似程度，从而实现对种群个体优劣的判断，选择优秀个体引导进化，解决算法选择压力下降的问题，引导种群向真实Pareto前沿收敛。

1）编码

侦察星座优化模型的决策变量中同时存在离散变量和连续变量。每个轨道面内卫星数和轨道面数都是离散变量，而常见的对于离散变量的处理中，去圆整的方法会导致决策变量变化速度过快，难以对接空间充分搜索，转化为约束的方式又会导致算法的复杂度急剧上升[15]。因此，作者在编码时将所有决策变量进行实数编码，在解码时通过映射使离散变量取值可行。设P为轨道面个数，S为每个轨道面内卫星数，h为轨道高度，inc为轨道倾角。编码格式如图6所示。

2）理想解

理想解是多目标优化问题中，每个子目标所能达到的最优状态的组合。对于M维多目标优化问题，本文分别将每个子目标作为唯一优化目标，通过多次单目标优化算法进行优化，并取其多次优化中所能达到的最优状态为有效解idj，将M个子目标的有效解组合，即可形成理想解ideal=id1，id2，…idM。

3）隶属度映射

隶属度刻画的是隶属程度，经过隶属度映射，可以有效避免量纲和数量级带来的影响。本文采用相对隶属度函数对算法中的解进行映射。对于子目标j，它的隶属度uj可表示为

uj=1，xij≤yj1xij-yj1yj2-yj1，yj1<xij<yj20，xij≥yj2（12）

其中，xij为第i个粒子的第j个子目标的值，yj1为第j个子目标的下限，通过多次进行单目标优化后取最小值得到。yj2为第j个子目标的上限，通过多次进行单目标优化后取最大值得到。为了避免出现某个子目标映射后的隶属度为0或1，导致后续无法计算模糊关联熵系数的情况，对求解的上限与下限进行处理，处理系数设为0.01。