基于有限元仿真结果识别的建筑物目标毁伤评估

摘 要：针对建筑物目标准确毁伤评估需求，提出一种基于有限元仿真结果识别的毁伤评估新方法。利用结构动力有限元分析软件SAP-2000进行目标毁伤数值模拟与分析，通过数值模拟结果的图像变化特征识别与指标量化，结合目标功能与物理毁伤等级判别准则，实现打击前的目标毁伤预评估。利用实例进行了仿真验证，结果表明，该方法在仿真条件下能够合理、有效实现建筑物目标的毁伤评估。

关键词：有限元仿真;建筑物;毁伤评估;数值模拟;特征识别

中图分类号：E920.8 文献标志码：A DOI：10.3969/j.issn.1673-3819.2024.04.020

引用格式：

王俊，雷宏宇.

基于有限元仿真结果识别的建筑物目标毁伤评估

.指挥控制与仿真，2024，46（4）：150-155.

WANG J，LEI H Y.

Building damage assessment based on finite element simulation results recognition

.Command Control & Simulation，2024，46（4）：150-155.

Building targets damage assessment based on

finite element simulation results recognition

WANG Jun， LEI Hongyu

（Beijing Aeronautical Technology Research Center， Nanjing 210028， China）

Abstract：Aiming at the demand for accurate damage assessment of building targets， a new damage assessment method based on finite element simulation results recognition is proposed. The structural dynamic finite element analysis software SAP-2000 is used for numerical simulation and analysis of target damage， and the pre-assessment of target damage before attack is realized by numerical simulation images feature recognition and quantization combined with the target functional and physical damage level discrimination criteria. The rationality and availability of the method are verified by the simulation of examples.

Key words： finite element; building; damage assessment; numerical simulation; feature recognition

收稿日期： 2023-06-03

修回日期： 2023-08-27

作者简介：

王 俊（1987—），男，工程师，博士，研究方向为毁伤效应研究。

雷宏宇（1995—），女，助理实验师。

地面建筑物目标作为潜在打击对象，打击前研究如何实现其有效、准确毁伤预评估具有重要军事价值与意义，能够为火力筹划、任务规划等提供必要的支撑。

目前，针对建筑物目标毁伤评估的研究主要包括以下两种：一是采用有限元软件实现战斗部对目标毁伤的全过程高精度仿真，该方法侧重于毁伤机理研究;二是合理简化建筑物和毁伤过程，通过建立工程计算模型实现毁伤评估。

国外对于建筑物毁伤评估的研究主要采用仿真与试验相结合的方法，研究弹药对建筑物预测毁伤评估方法。Bogosian等提出了一种框架结构的复杂ADINA模型与简化工程模型相结合的方法［1］，建立了建筑物对载荷响应的快速计算模型;Remennikov研究了几种可用于预测复杂几何结构建筑物承受爆炸载荷的分析方法［2］，分析了建筑群在受爆炸载荷时相邻建筑的影响;Magnusson等通过试验测试了高强度和普通强度钢筋混凝土梁受到爆炸载荷和静态加载下的性能［3］; Krauthammer等通过试验研究了载荷与结构特性对 P-I曲线的影响，评估了脉冲形状、上升时间与阻尼等对P-I曲线的影响［4］。国内对于建筑物毁伤评估研究多数基于有限元仿真与工程计算模型。李伟等基于峰值超压分布模型，提出了建筑物体积毁伤概率的概念及相关计算方法［5］;肖黎等通过流固耦合算法模拟了建筑物在内爆载荷作用下的破坏过程，得到了建筑物框架结构的毁伤范围［6］;李恩奇、陈旭光等对建筑物在多发弹药打击下的累积毁伤效果进行了仿真分析［7-8］;张重阳等提出了通过爆炸试验与试验原型数值模拟，研究了侵爆弹对框架类建筑物毁伤效果的评估方法［9］;周阳等基于工程计算模型建立了弹药打击下钢筋混凝土楼房的毁伤评估方法［10］;曹宇航等采用数值计算方法，开展了典型工况、爆炸作用下迎爆方向砌体墙的连续毁伤效应与房间内冲击波传播规律的研究［11］。

第二步：专家主观评判。专家根据个人主观经验对每个抽样点合格、不合格和不确定的可能性进行评判，同一点三类可能性之和必须等于1。

第三步：利用证据理论综合处理。对于同一组抽样点，不同专家的评判结果可能得到不同的隶属度分配函数。按照证据理论方法，计算这些隶属度分配函数的正交和，将多个专家的评判结果进行综合。

第四步：三隶属度支持向量机模型处理。根据三隶属度支持向量机模型方法，利用Matlab工具，对所有抽样点综合后的结果进行处理，生成分类超面K。超面K与坐标轴包围的范围就是所求的需求空间。位于超面K内的点都合格，位于超面外的点都不合格。

第五步：测试验证并调整。第四步得到的只是初步的需求空间，还需进行测试验证，误差的阈值根据需求进行调整，本文定为0.1，即随机采用生成的需求空间与专家评判结果进行比对，误判率不大于0.1。如果存在较大误差，则要分析以上哪个环节存在问题。一是检查抽样点是否足够，如果抽样点过少且抽样点间距离未达到最小分辨率，则考虑插入新增抽样点进行细化。二是验证专家评判情况是否合理和专家人数是否足够，如果某专家评判出现矛盾现象较多，则考虑更换专家；如果专家人数过少，则考虑增加专家数量。三是验证三隶属度支持向量机分类错误量与点到超面距离之间的关系是否合理，可由常量C来调整。通过上述三方面的验证和调整，便可得到最终需求空间。

3 方法原理

3.1 评判表的生成

评判表建立的前提是在确定了评估指标。生成评判表分为以下两步：

1）设定各指标的抽样取值范围。每个能力指标都有一个取值范围，根据具体问题将其取值范围设定为一个合理的区间。

2）选取抽样点。选取抽样点的方法有全排列抽样、正交抽样、拉丁方抽样和均匀设计等。指标取值范围的两个端点包含在需选取的抽样点之内，但通常情况下，只有这两个端点是不够的，需在取值范围内根据需要增选一定数量的抽样点。本文采用全排列抽样，新增抽样点在原两抽样点距离等分处选取。如选取1个新增抽样点时，新增抽样点选在12处；选取2个新增抽样点时，新增抽样点选在13、23处。若某指标体系W共有N个指标w1，w2，…，wN，指标wi在其取值范围内插入了mi个新增抽样点，因此评判表全排列抽样点共有m1+2m2+2…mN+2个。当指标数较少时，可以选取多个抽样点。但指标数大于3时，选取多个抽样点时可能会带来维度灾难，数量巨大的抽样点会使专家难以完成评判。因此，在指标数大于3时，每个指标通常在取值范围内取不多于2个抽样点。

在完成以上两步后，可能会存在抽样点数量不够的情况。如果某指标相邻抽样点间距离大于专家可区分的最小分辨率时，则考虑插入一定数量的新增抽样点进行细化。如图2，经过全排列抽样得到a1、a2、a3、a4、b1、b2、b3、b4等8个点，但是相邻点间距离未达到最小分辨率，则分别在三个指标区间内插入一个点进行全排列抽样。

3.2 抽样点细化区的筛选

由于复杂系统指标空间的非线性和不均匀性，有些区域必须要细化，有些区域可保持原状，因此只需对前者进行细化处理，就可以减少一些不必要的计算量。特别是对于多维指标空间，尤为重要。

本文建立的指标需求空间是单调的。如果某一点符合要求，那么数值优于该点的所有点都符合要求；如果某一点不符合要求，那么数值劣于该点所有点都不符合要求。

如图3，在a、b和d方格中，四个顶点全为合格，根据单调性，这方格中所有点都合格。同样，i方格内所有点都合格。在a、b、d、i这4个方格内不存在分类的交界面，对其细化对找到分类超面没有意义。因此，只保留其原顶点信息而不进行下一步细化。只需在合格点与不合格点共存的g、h、e、f、c等5个方格进行细化即可。不难发现，需要细化的5个方格有一个共同的特点，就是最优点与最劣点分类相异。据此，形成如下原则：

细化原则对N维单调指标空间中单元格进行细化时，如某一N维单元格中最优点与最劣点分别属两类，则需作进一步细化；如该单元格的最优点与最劣点同属一类，则不需再作细化。

关于是否同类的判断可以采取以下简单原则：比较各个点合格的可能性减去不合格的可能性的值，如果结果都大于某一指定的正数，则认为它们属合格类，如果都小于某一指定的负数，则认为属不合格类。其他情况都判为不确定类。指定的数可以根据决策问题与决策者偏好来确定。

3.3 专家评判

3.3.1 专家的选择

规模合理、结构科学、权威性强的专家群体是保证评估正确性的基础。选择专家时，必须要遵循以下三个原则：

1）权威原则

参加评判的专家必须长期从事被评估内容所属的领域工作，经验丰富，领域情况熟悉，在评估对象领域内有较高的理论造诣和实践经验，具有较高的知名度。

2）多资历原则

不同资历的专家思维特点不同。一般而言，资历长的专家考虑问题全面，但易偏于谨慎；资历短的专家勇于开拓，看待问题角度新颖，但易存在片面性。因此，选择专家群应包括不同资历的专家，以形成优势互补。

3）人数适度原则

专家数量只需使评估达到客观性、全面性即可。专家人数过多，会增加工作的时间和费用，难以形成一致的评价结果；过少，则会导致最终结论的片面性和主观性。

3.3.2 评判方式

每名专家对评判表上每一个抽样点都要给出相应的评判。评判要遵循以下原则：

1）评判选项分为合格、不合格和不确定三类；

2）评判结果根据专家个人知识与经验给出；

3）每名专家要给出每个抽样点的合格、不合格和不确定的可能性，可能性的取值范围为[0，1]，同一点的三类可能性之和等于1。

3.4 基于证据理论的专家判断综合

证据理论比概率论更合适于专家系统推理方法，具体算法可参考文献[7]。下面对如何运用该算法对专家评判结果进行综合处理进行示例说明。

设D＝{合格，不合格}，M1、M2是两个专家对某抽样点的判断，通过证据推理算法合并专家判断。

M1合格，不合格，合格，不合格，={0.3，0.5，0.2，0}

M2合格，不合格，合格，不合格，={0.6，0.3，0.1，0}

K=1-∑X∩Y=φM1X×M2（Y）=

1-［M1合格×M2不合格+M1不合格×M2合格］＝

1-［0.3×0.3+0.5×0.6］=0.61

M合格=K-1×∑X∩Y=φM1X×M2Y=

10.61×［M1合格×M2合格+M1合格×M2合格，不合格+M1合格，不合格×M2合格］=

10.61×［0.3×0.6+0.3×0.1+0.2×0.6］＝0.54

同理可得

M不合格＝0.43M合格，不合格＝0.03

所以，经对M1与M2进行组合后得到的隶属度分配函数为

M合格，不合格，合格，不合格，={0.54，0.43，0.03，0}

3.5 三隶属度支持向量机

为提高分类的精确性，文献[8]引入隶属度的概念，提出了模糊支持向量机。其主要思想是，如果发现训练点远离所属类中心区，就降低输入点划分为其中一类的隶属度。本文对该方法作了改进，提出一种新的模糊支持向量机。即在发现训练点远离而降低输入点划分为其中一类的隶属度的同时，也要提高该点划分为相反一类的隶属度。此外，训练点还存在不确定的可能，即该点既可能属于其中一类，又可能属于相反的一类，也被赋了一个隶属度，这三个隶属度就是3.4中证据理论结果的三个主观隶属度。需要注意的是，三个隶属度之和等于1。普通模糊支持向量机的抽样点只有一种隶属度，本文的模糊支持向量机有三种隶属度。因此，权且将本文提出的向量机称为三隶属度支持向量机。

普通模糊支持向量机中，每个学习点是以

{xk，yk，sk}，k=1，2，…，N（1）

的方式给出，每个点只属于两类中的其中一类，隶属度为sk。

基于三隶属度支持向量机原理，对于每一个点，应当给出该点分别属于两类以及不确定分类的隶属度。不确定分类的隶属度等于1减去两类隶属度之和，因此只需给出该点分别属于两类的隶属度即可。数据量由以前的N个变成了2*N个。每个点是以

xk，1，mk，xk，-1，nk，k=1，2，…，Nmk+nk≤1，0≤mk≤1，0≤nk≤1（2）

的方式给出。其中，{xk，yk，mk}中，xk是给每点输入的k维向量，yk是观察结果，mk是xk划分为1的隶属度，nk是xk划分为-1的隶属度。

分类问题可以表示为

minω，α，ξk，ηkζω，b，ξk，ηk=12ωTω+C∑Nk=1［mkξk+nkηk］

Subject to：ωTφxk+b≥1-ξk k=1，2，…，N

ωTφxk+b≤-1+ηk k=1，2，…，N

ξk≥0 k=1，2，…，N

ηk≥0 k=1，2，…，N（3）

给约束条件αk，βk，μk和υk引入相应的拉格朗日多项式，我们建立相应的拉格朗日方程式：

Min Jω，b，ξk，ηk，αk，βk，μk，υk＝12ωTω+

C∑Nk=1mkξk+C∑Nk=1nkηk-∑Nk=1αk（ωTφxk+b-1+ξk）+

∑Nk=1βk（ωTφxk+b+1-ηk）-∑Nk=1μkξk-∑Nk=1υkηk（4）

对ω、b、ξk、ηk进行求导

ddωJ=ω-∑Nk=1αkφ（xk）+∑Nk=1βkφ（xk）=0

ddbJ=-∑Nk=1αk+∑Nk=1βk=0

ddξkJ=Cmk-αk-μk=0 k=1，2，…，N

ddηkJ=Cnk-βk-υk=0 k=1，2，…，N（5）

然后根据文献[7]的学习算法，我们得到以下分类函数：

yx=signωTφx+b= sign∑Nk=1αk-βkKx，xk+b（6）

本文将式（6）作为三隶属度模糊支持向量机得出的最终评判结果。

4 案例分析

本文以某虚拟的战斗机作战指标主观需求空间的生成为例，对所提方法的使用过程进行说明。

4.1 初步全排列抽样，专家进行评判

4.1.1 建立指标空间，生成全排列评判表

假定某战斗机在突击某类目标时的关键突防能力指标可由RCS值、最大巡航速度V、自卫干扰系数W三者构成。通过调查，当RCS大于1时，几乎所有专家都认为此种战斗机的RCS值已经超出可接受范围，即100%不合格；而目前技术力量又无法让RCS值小于0.1，因此，RCS的取样范围为0.1～1，可以初步将取样点定为0.5。同理，最大巡航速度V的取样范围为0.8～2.5Ma，取样点定为1.6；自卫干扰系数W的取样范围为0.1～1，自卫干扰系数是以基于自卫干扰功率、增益等指标综合而成的一个系数，取样点定为0.5。

由以上可知，抽样点定为由上述取样点构成的全排列组合，共有3*3*3＝27个，抽样点表示方式为（RCS，V，W），如下所示：

0.1，0.8，0.10.1，0.8，0.50.1，0.8，1

0.1，1.6，0.10.1，1.6，0.50.1，1.6，1

0.1，2.5，0.10.1，2.5，0.50.1，2.5，1

0.5，0.8，0.10.5，0.8，0.50.5，0.8，1

0.5，1.6，0.10.5，1.6，0.50.5，1.6，1

0.5，2.5，0.10.5，2.5，0.50.5，2.5，1

1，0.8，0.11，0.8，0.51，0.8，1

1，1.6，0.11，1.6，0.51，1.6，1

1，2.5，0.11，2.5，0.51，2.5，1

4.1.2 多个专家评判，形成评判结果

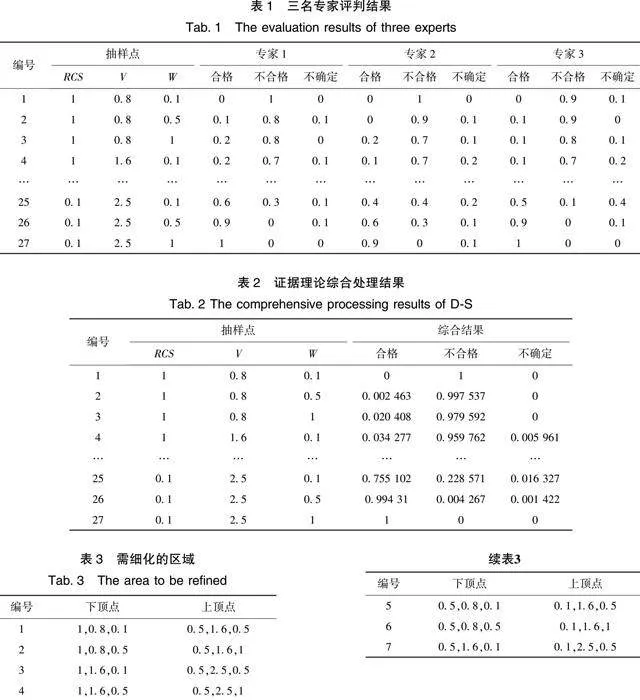
假定邀请3名专家进行评判，得到结果如表1所示。

4.2 利用证据理论综合结果

运用证据理论综合所有专家的评判数据，得到每个抽样点的处理结果，如表2所示。

4.3 筛选需细化的区域

通过部分测试，抽样点还不充分，需要进一步增加抽样点。由4.1.1可知，RCS取值范围为[0.1，1]，V的取值范围为[0.8，2.5]，W的取值范围为[0.1，1]，后来RCS、V、W分别加入了1个抽样点，因此RCS、V、W组成的三维空间被分成了2*2*2＝8个方格。

经过筛选之后，按照细化原则，留下7对顶点，即7个方格，为了叙述方便，本文将距离坐标原点最远的点称为上顶点，将距离坐标原点最近的点称为下顶点。7对顶点分别如表3。

4.4 对新增抽样点进行全排列、评判和综合处理

4.4.1 细化筛选区域

在上一步得到的7个方格再插入取样值进行等分，得到一系列抽样点，并对抽样点进行选择。

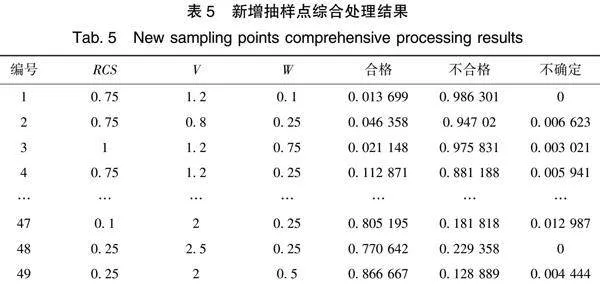
例如，在下顶点为（1，0.8，0.1）、上顶点为（0.5，1.6，0.5）的方格中，RCS、V、W分别插入0.75、1.2、0.25便可等分。插值后，方格被分为了8个小方格，共有27个点，除去原有8个点，插值后新产生了19个点。在这19个点中，一些位于原方格边上的点，如（1，1.2，0.1）（0.75，0.8，0.1）（1，0.8，0.25）等，使专家在评判时很难准确地进行分辨，因此在选择时，将这些点舍去，只留下与大方格的8个点不在同一边上的点，如（0.75，1.2，0.1）。经过选择，得到以下7个点，7个方格共选择得到49个点。

4.4.2 评判新增抽样点

三位专家对新增的49个点进行评判，结果如表4所示。

4.4.3 数据综合处理

利用数据理论对49个新增抽样点数据进行综合处理，结果如表5所示。

4.4.4 对两次评判综合结果进行合并

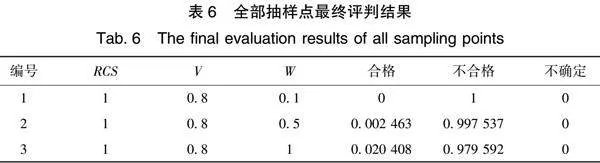
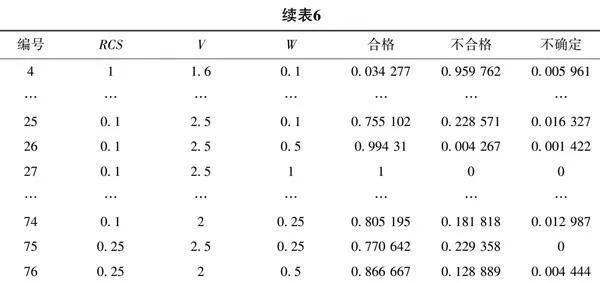
初步评判时有27个点，再次评判时新增49个点，合并之后便有76个点的评判结果，如表6所示。

4.5 利用三隶属度模糊支持向量机方法生成需求空间

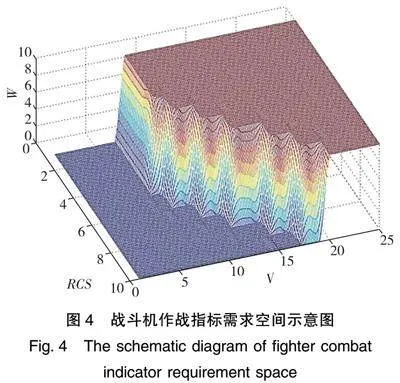
通过Matlab 软件编程，由76个抽样点评判结果，可以求出分类的支持向量，然后运用SVM画图命令“svmplot”画出某型战斗机作战指标主观需求空间的示意图，为了便于显示，三个指标都做了整数化处理（扩大10倍显示），如图4所示。

图4中，被包围部分就是所求的战斗机作战指标需求空间，只要战斗机的三个指标落在需求空间内，便认为该战斗机满足作战需求。该需求空间可以作为后续各类型能力指标分析与设计的基础[5]。该案例中战斗机的RCS值、最大巡航速度V、自卫干扰系数W都属于抽象指标，直接受到评判主体认知水平、个人好恶等主观因素的影响，使用客观方法难以建立相应的需求空间。本文方法不仅可以对上述类似案例进行效能评估，也可以运用到多指标复杂系统问题中，这为复杂系统效能评估提供可量化准则。

5 结束语

本文对无法采用传统方法和借助仿真实验获取需求空间的复杂系统抽象问题进行了探索。通过实验设计、专家评判、证据理论综合和三隶属度模糊支持向量机处理等步骤，可以获得一些复杂系统抽象问题的需求空间。本文提出的主观需求空间生成方法，对于基于需求空间能力指标论证问题有支撑作用。但该方法与其他客观方法一样，在生成需求空间的过程都面临难以减少计算量的困难。下一步主要的研究工作，一是深入研究抽样实验方法，即如何用最少的抽样判断点获取最准确的主观需求空间。二是如何运用粗集与模糊集工具，进一步深入标度主观需求空间。

参考文献：

[1] 何能波， 吴红朴， 孙金， 等. 基于模糊层次分析法的ADC模型导弹部队装备保障效能评估[J]. 指挥控制与仿真， 2022， 44（6）： 41-45.

HE N B， WU H P， SUN J， et al. Evaluation of missile force equipment support effectiveness based on ADC model[J]. Command Control & Simulation， 2022， 44（6）： 41-45.

[2] HU J W， HU X F， ZHANG W M， et al. Monotonic indices space method and its application in the capability indices effectiveness analysis of a notional antistealth information system[J]. IEEE Transactions on Systems， Man， and Cybernetics-Part A： Systems and Humans， 2009， 39（2）： 404-413.