基于稳态系数的装备维修器材库存调剂方法研究

摘 要：针对目前不同装备维修器材保障节点库存积压和缺货等待并存、库存量在整个保障网络中分布不均等问题，将同级保障网络中的单个保障节点按照库存水平、保障节点之间的支持度、保障节点所在保障区域的需求状况、发生需求不能满足时的风险成本等相关参数生成描述其调剂能力的稳态系数，在此基础上生成全网的稳态系数。根据稳态系数与设定阈值之间的差距，按照相应算法流程进行主动调剂，同时结合缺货引发的被动调剂，可极大提高器材调剂工作的科学化、自动化、智能化水平，进而提高维修保障成功率。

关键词：维修器材；调剂；库存；稳态

中图分类号：E921；TP18

文献标志码：A DOI：10.3969/j.issn.1673-3819.2024.04.004

Research on inventory adjustment method of maintenance

equipment based on steady-state coefficient

引用格式：

鱼静，施宁，方星星.基于稳态系数的装备维修器材库存调剂方法研究

.指挥控制与仿真，2024，46（4）：28-34.

YU J，SHI N，FANG X X.Research on inventory adjustment method of maintenance equipment based on steady-state coefficient

.Command Control & Simulation，2024，46（4）：28-34.

YU Jing， SHI Ning， FANG Xingxing

（PLA Army Academy of Artillery and Air Defense， Hefei 230031， China）

Abstract： Arming at the coexistence dilemma of inventory overhang and shortage of different maintenance equipment supply nodes， a steady-state coefficient of a supply node has been described with which contains inventory level， the support degree between nodes each other， the demand status of the area guaranteed by the node and the cost of risk when the demand cannot be met. The steady-state coefficient of the inventory network was calculated on the base of all of support nodes. The active adjustment is carried out flowing the corresponding algorithm according to the gap between the steady-state coefficient and the threshold which has been set before. The scientific， automatic and intelligent level of equipment adjustment can be greatly improved， consequently the success rate of maintenance support is improved if the passive stock adjustment is combined because of out of stock at the same time.

Key words：maintenance equipment; adjust; inventory; steady state

收稿日期： 2023-07-18修回日期： 2023-11-07

作者简介：

鱼 静（1976—），女，博士，副教授，研究方向为军事运筹分析，系统仿真。

施 宁（1981—），男，硕士，讲师。

装备维修器材（以下简称“器材”）作为实施装备维修保障的重要物质基础，在装备维修保障流程中具有重要的地位和作用。当前，装备维修保障节点间库存积压和缺货等待问题两者并存，原因主要有：1）装备更新换代速度加快，不断有老旧型号装备退出现役，其关联的器材产生呆滞和积压，而新列装的装备关联器材容易产生短缺；2）需求的复杂性使得维修器材的消耗规律愈发难以把握，单纯依靠历史数据和人工经验的需求预测方法越来越难以应对库存的变化；3）部分基层单位没有严格落实修理规范，致使按照维修计划申领的器材没有按照计划消耗掉，造成积压。这些因素相互交织叠加，致使库存活力变差，高库存与高库龄在部分保障点矛盾突出。调剂是在保持库存总量不变的前提下优化库存结构的有效手段，其目标是运用调入调出完成各保障节点库存数量重组和全局库存结构性重塑。装备维修器材中占比最大的是通用器材，这一部分是供应节点之间完全可以无差别共享的，也是调剂关注的重点对象。其余的专用器材也可进行互通有无，甲的淘汰或停用器材可能是乙目前有需求的缺货器材。当前迫切需要具有科学性、前瞻性的智能辅助调剂方法来协助人工完成调剂方案的生成与决策。

1）运输机无法中途停留。

2）运输机速度取固定值。

3）运输机在各前线阵地之间按照直线飞行。

4）物资进行标准化打包，取值为离散变量，采用空投方式进行补给。

5）运输机数量和库存物资数量不设上限约束。

6）各点位对物资的需求小于单架运输机的载荷能力。

1.3 数学模型

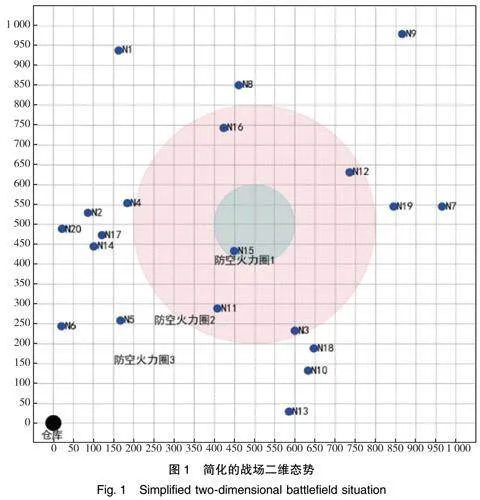
本文将待补给点位简化为平面上的坐标点，设为{N1，N2，…，N20}，将参与任务的运输机群设为一个集合{V1，V2，…，Vs}，下标s表示出动的运输机数量。运输机的飞行速度设为v，最大载货量设为30，单机最大航程设为30 000（数据均为无量纲值）。

本文任务规划模型将任务分配与路径规划合并，目标是为每一架出动的运输机规划一个任务序列，同时确定该运输机的具体装载以及出发时间。在完成投送补给任务时，模型希望能够平衡运输机的损失、运输机总航程、各点位的按时受补给率。模型的目标函数由以下三部分组成：

1）总航程为全部运输机在执行任务过程中的总通过距离。

2）运输机损失为完成任务后损失的运输机数量。

3）未按时受补率，表示补给点位是否能够按时收到补给。

总航程由所有运输机的航程构成，对于任意指定的运输机Vk，其任务序列表示为Mk：{Tk | Nk0， Nk1， Nk2， …， Nkl， Nk0}。Mk表示运输机在Tk时刻从仓库出发，依次途经k个前沿补给基地后返回仓库。如果在任务执行过程中未被击落，则单个运输机的总航程为上述各点之间欧拉距离d的累加，表示为

Dk=dNk0，Nk1+dNk1，Nk2+…+Nkl，Nk0（1）

由于后续设计了运输机战损作为目标函数的子项，因此为了避免重复统计，若运输机在飞行过程中遭到击落，则不再统计该机被击落前的航程。假设共出动s架运输机，最终成功返回t架，则总航程可以表示为

f1=∑ti=1Di（2）

运输机的战损由被击落的运输机数量来表示，即

f2=s-t（3）

未按时受补率由未能及时送达的补给数量和偏离时间构成，若某前沿补给阵地需在时间窗口[Ta，Tb]之间补给p个物资，但实际补给中存在q个物资未能按时到达，总任务持续时间为To，则该阵地单个未按时到达的物资可用如下公式表示：

完成了投送但未按时投送：

Oq=min（absT-Ta，absT-Tb）To（4）

未能在总任务持续时间内完成投送：

Oq=1（5）

对于到达时刻为T，但未能按时抵达的物资，需要按照迟到或者早到的时间计算惩罚函数，该值位于（0，1）区间内。若未能完成补给，其目标惩罚函数记为1。因此所有阵地的未按时受补率是所有未按时到达物资惩罚函数的累加：

f3=∑20i=1∑qj=1Oij（6）

为三个目标函数分别赋权重α1，α2，α3，得到整个优化问题的数学描述：

min α1f1+α2f2+α3f3（7）

s.t. Dk≤30 000，k∈1，s

上述问题为组合优化问题，考虑采用启发式算法进行全局优化。

2 优化算法构建

2.1 基础遗传算法

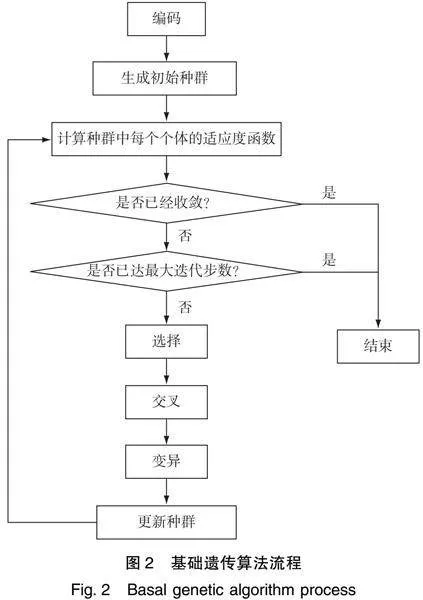
遗传算法是一种基于直观经验构造的经典启发式算法，在处理解决多旅行商类问题时，可利用程序模拟生物染色体执行交叉变异等操作，通过种群迭代的过程来实现最终寻优。算法通用流程如图2所示。

利用遗传算法解决问题的关键是建立有效的编码和解码方案，同时设计合适的选择、交叉和变异算子。具体编码方案如下：初始种群中的一个初始解由s条染色体构成，表示出动s架次运输机执行s个任务序列。每条染色体为包含21个变量的数组，前20个整数表示途径的路径，第21个实数变量表示出动时间。任一初始解中包含的变量共21*s个，s取[1，20]范围内的任意整数。

适应度的计算采用建立的目标函数，选择操作采用轮盘赌法和精英策略，保留每轮迭代过程中表现最佳的前10%的个体，确保遗传算法最终能够收敛。交叉算子为初始解内部变异，即按照预设的交叉因子概率性交叉初始解内部的两条染色体。变异算子则在单个染色体上进行局部突变，防止遗传算法过早陷入局部最优解，同时增加运输机架次的变异。

2.2 融合先验知识的改进遗传算法

由于通用遗传算法求解效率较低，考虑采用将先验知识融入遗传算法，用以改善收敛的速度和精度。算法改进的主要思路是在生成初始种群、交叉和变异的完全随机方法中融合“任务合并”和“饱和补给”的思想。“任务合并”指的是将若干个投送任务安排到一架运输机的任务序列中。“饱和补给”是指考虑到运输机有被击落的风险，考虑同时出动若干架冗余运输机对其进行重复补给。

首先，定义补给点位之间的空间距离和时间距离，空间距离即欧拉距离，用函数d表示，时间距离e定义如下：

e（Nx，Ny）=absTax，Tbx+dNx，Nyv∩［Tay，Tby］（8）

时间距离e具有有向性，表示时间窗口x与时间窗口y之间的重叠范围。算法分别建立两张20*19的表格，存储各阵地之间空间距离和时间距离，以供查询使用，避免后续重复计算。

随后，算法新增3个超参数，即空间距离阈值，时间距离阈值和按时投送期望阈值，用于调整搜索空间的大小。改进后的遗传算法流程如图3所示。

融合先验知识生成初始种群/个体的方法步骤，如图4所示。

Step1：随机生成一个[1，20]之间的整数i，用于确定初始个体第一条染色体中数值1的位置。计算i阵地与仓库之间的空间距离、飞行所需的时间与出发时间。如果该值小于零，则令出发时间等于0，如式（9）所示。

Ti=max（Tai-dNi，N0v，0）（9）

Step2：按照生成的空间距离和时间距离阈值，对比查表获得的i阵地到达其他阵地的时间/空间距离，同时满足小于空间距离阈值并且大于时间距离阈值的阵地将被筛选出来，可供后续继续随机选择。

Step3：根据该阵地对物资的需求计算运输机剩余载荷，同时根据该阵地与仓库之间的距离计算运输机的剩余航程，一旦剩余载荷等于0或者剩余航程不足以支持返航，则放弃本次抽取。

Step4：依据上述3个步骤完成一个初始解中第一条染色体的生成，第二条染色体在抽取第一个目标阵地时，需要排除上一条染色体中除最后一个抵达阵地以外的所有已达阵地。

Step5：当所有的阵地点都已经出现在了染色体的非最后一位非零值中，则表示所有点已补给完毕。此时原则上停止生成新的染色体，但考虑到可能存在无法按照预期完成投送的情况，因此需要额外生成数条冗余任务序列。

Step6：针对已生成的所有染色体中的飞行路线和击落概率计算每个阵地的按时补给期望，然后按照设定的按时补给期望阈值进行筛选，将所有小于该阈值的m个阵地挑出来。按照Step1—Step3的方式重新生成m条独立的冗余染色体，与之前第4步中已经生成的染色体构成一个完整的初始个体。

Step1—Step6多次重复，即可生成一个完整的初始种群。

3 优化结果与分析

3.1 实验参数设定

算法将上述数学模型中的符号参数进行数值化，如表1所示。

此外，随机生成一组各补给点位的物资需求和时间窗口，时间窗口的持续时长取值范围[0.5，2]，物质需求数量均为整数，取值范围[5，15]，具体数值如表2所示。

3.2 不同优化算法的对比

作者选取基础遗传算法、改进的遗传算法和基准投送策略分别进行对比。基准投送策略指的是对每一个补给点位出动一架运输机进行补给的策略。基础遗传算法和改进遗传算法，均设定最大迭代步数为1 000代，初始种群规模为100，变异率0.1，交叉率0.2。

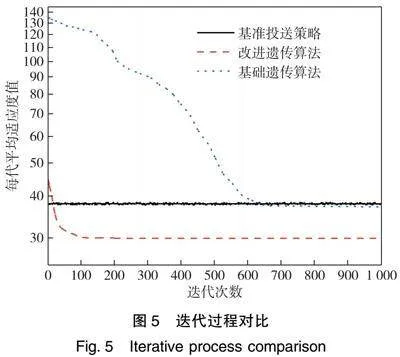
改进的遗传算法，设置3个超参数的取值范围如表3所示，其优化过程如图5所示。

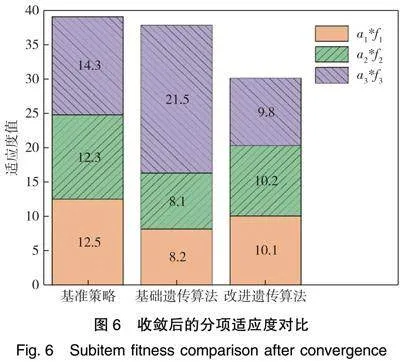
由图5可知，基准投送策略不存在迭代，目标函数值基本稳定在38.1。基础遗传算法起始的种群平均适应度值在130以上，且收敛较慢，直到550代之后才能逐渐收敛至基准投送策略的水平，最终收敛获得的结果为37.8。改进后算法由于在生成初始种群时就已经限定了生成范围，起始的种群平均适应度值为45，且在60代即可收敛至30.1。这一结果与基准策略取得的38.1相比，适应度值下降了21%。而与基础遗传算法相比，其收敛速度则提高了10倍。算法收敛后获得的3个适应度值，具体的分项适应度对比如图6所示。

3.3 优化结果分析

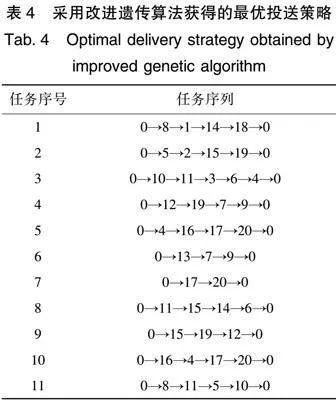
表4包含11条任务序列，即代表出动了11架运输机执行补给任务，比基准策略中的20架运输机减少了近一半，完整的补给路线如图7所示。

由图7可以看出，大部分的阵地受到了两次补给，尤其是位于防空火力圈2和防空火力圈1中的阵地，受补给的次数甚至超过2次，确保了高风险航线上的阵地能够接受补给。

3.4 超参数的影响

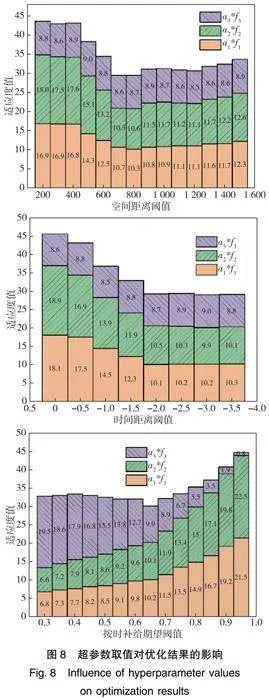
根据改进遗传算法的优化结果可知，3个超参数最终收敛于[734.8，-1.95，0.63]，因此后续以这一组超参数作为基准，进一步深入分析3个超参数对优化结果的具体影响，如图8所示。

由图8可以看出，在空间距离阈值小于500时，由航程带来的适应度分项值α1f1 始终较大，这是由于难以找到可供合并的任务，因此绝大部分的任务序列都只能对一个阵地进行投送，导致总航程较长。由于总航程较长，运输机被击落的概率也会随之增加，α2f2也较大。此外，由于存在冗余任务序列，未按时受补带来的适应度分项值α3f3始终变化不大。由于按时补给期望阈值影响的是冗余任务序列的数量，如果该值设得较小，则意味着冗余任务序列较少，那么α1f1和α2f2都会比较小，而α3f3则会变得较大。如果该值设得较高，则冗余任务序列则会变得过多，α1f1和α2f2都会变得较大，从而抵消了α3f3减小带来的收益。

总之，适当放宽阈值可以有效改善收敛结果，但并非越高越好，一旦越过某个界限后，继续放宽阈值带来的收益就会变小，甚至会降低，且算法收敛的速度会变得更慢。

4 结束语

本文针对存在干扰源和时效性要求的多运输机物资投送任务规划问题进行了研究，在求解总航程、投送战损以及未按时受补率的目标函数时，提出并验证了融合“任务合并”和“饱和补给”先验知识的改进遗传算法的优化效果，最终收敛的优化结果不仅令目标函数值下降了20%，而且令收敛速度提高了10倍，且进一步通过对模型超参数的分析，提出合理设置参数值的可行建议。上述结果表明融合了先验知识的进化算法在求解大搜索空间的复杂问题中的明显优势，但本文获得的优化结果仍然是一个集中式控制和离线的优化方案，后续可结合实际场景，针对时间窗口多次打开、动态投送需求、分布式控制和在线实时优化等问题展开进一步的深入研究。

参考文献：

[1] 戴健， 许菲， 陈琪锋. 多无人机协同搜索区域划分与路径规划[J]. 航空学报， 2020， 41（S1）： 149-156.

DAI J， XU F， CHEN Q F. Multi-UAV cooperative search on region division and path planning[J]. Acta Aeronautica et Astronautica Sinica， 2020， 41（S1）： 149-156.

[2] 张安， 杨咪， 毕文豪， 等. 基于多策略GWO算法的不确定环境下异构多无人机任务分配[J]. 航空学报， 2023， 44（8）： 148-164.

ZHANG A， YANG M， BI W H， et al. Task allocation of heterogeneous multi-UAVs in uncertain environment based on multi-strategy integrated GWO[J]. Acta Aeronautica et Astronautica Sinica， 2023， 44（8）： 148-164.

[3] 张安， 毕文豪， 邱鹏， 等. 基于改进合同网的多UAV打击地面TST任务重分配[J]. 战术导弹技术， 2019（2）： 39-46.

ZHANG A， BI W H， QIU P， et al. Mission re-assignment for attacking ground TSTs with multi-UAVs based on improved CNP[J]. Tactical Missile Technology， 2019（2）： 39-46.

[4] 凌富园， 杜承烈， 孙宝亮， 等. 基于不规则障碍物环境下无人机的改进几何路径规划算法[J]. 航空电子技术， 2019， 50（4）： 40-46.

LING F Y， DU C L， SUN B L， et al. An improved geometrical path planning algorithm for UAV in irregular-obstacle environment[J]. Avionics Technology， 2019， 50（4）： 40-46.

[5] 张富震， 朱耀琴. 复杂环境中多无人机协同侦察的任务分配方法[J]. 系统仿真学报， 2022， 34（10）： 2 293-2 302.

ZHANG F Z， ZHU Y Q. Task allocation method for multi-UAV cooperative reconnaissance in complex environment[J]. Journal of System Simulation， 2022， 34（10）： 2 293-2 302.

[6] KUMAR S， PANDEY K K， MUNI M K， et al. Path planning of the mobile robot using fuzzified advanced ant colony optimization[C]//DEEPAK B， PARHI D， JENA P. Innovative Product Design and Intelligent Manufacturing Systems. Singapore： Springer， 2020： 1 043-1 052.

[7] 刚桂虎， 赵显. 多旋翼无人机在战术后勤中的应用分析[J]. 国防科技， 2016， 37（5）： 56-59， 75.

GANG G H， ZHAO X. Application and analysis of multi-rotor UAV in tactical logistics[J]. National Defense Science & Technology， 2016， 37（5）： 56-59， 75.

[8] 王国陈. 空中联合投送任务规划仿真与效能评估系统[J]. 系统仿真学报， 2022， 34（11）： 2 497-2 506.

WANG G C. Simulation and effectiveness evaluation system for joint delivery mission planning of airlift fleets[J]. Journal of System Simulation， 2022， 34（11）： 2 497-2 506.

[9] 刘佳明. “中转站+无人机空运”在战术投送保障中的运用[J]. 军事交通学院学报， 2019， 21（1）： 60-64.

LIU J M. Application of transit station and unmanned aerial vehicle transport modes in tactical delivery support[J]. Journal of Military Transportation University， 2019， 21（1）： 60-64.

[10]杨海根， 孙旺， 李禄阳， 等. 一种基于禁忌搜索算法的空中物资投送路径规划方法： CN111898818A[P]. 2020-11-06.

YANG H G， SUN W， LI L Y， et al. Aerial material delivery path planning method based on tabu search algorithm： CN111898818A[P]. 2020-11-06.

[11]李绍斌， 姜大立， 方海洋， 等. 基于车载模式的战场物资多无人机联合配送任务分配研究[J]. 军事运筹与系统工程， 2020， 34（3）： 19-25.

LI S B， JIANG D L， FANG H Y， et al. Research on task assignment of multi-UAVs joint distribution of battlefield materials based on vehicle-mounted mode[J]. Military Operations Research and Systems Engineering， 2020， 34（3）： 19-25.