考虑RMS因素的装备论证多方案分析方法

摘 要：提出一种考虑RMS因素的装备论证多方案分析方法。建立装备论证过程中的多方案分析框架，并给出装备论证多方案分析指标体系。通过分析对多方案具有影响的RMS和费用因素建立这些因素的量化模型。结合基于数据包络法的多方案分析模型及应用示例，说明方法的可行性和有效性。

关键词：可靠性;维修性;保障性;装备论证;多方案分析;数据包络法

中图分类号：E242 文献标志码：A DOI：10.3969/j.issn.1673-3819.2024.04.003

引用格式：

吕学志，冯晓容，谢智歌.

考虑RMS因素的装备论证多方案分析方法

.指挥控制与仿真，2024，46（4）：22-27.

LYU X Z，FENG X R，XIE Z G.

Analysis of alternatives for equipment demonstration considering RMS factors

.Command Control & Simulation，2024，46（4）：22-27.

Analysis of alternatives for equipment demonstration considering RMS factors

LYU Xuezhi1， FENG Xiaorong2， XIE Zhige3

（1. Unit 32179 of PLA， Beijing 100021， China; 2. Unit 32180 of PLA， Beijing 100072， China;

3. Military Science Academy， Beijing 100091， China）

Abstract：This paper presents a method of equipment demonstration AoA method considering RMS factors. It puts forward the equipment demonstration AoA framework， and elaborates equipment demonstration AoA measure system. It analyses the RMS and cost factors， and establishes their quantitative models. An AoA model based on Data Envelopment Analysis （DEA） and an application example are given to illustrate the feasibility and effectiveness of the method.

Key words：reliability; maintainability; supportability; equipment demonstration; analysis of alternatives; data envelopment analysis

收稿日期： 2023-06-14修回日期： 2023-07-20

*基金项目：中国博士后科学基金（2017M613360）

作者简介： 吕学志（1979—），男，博士，副研究员，研究方向为作战指挥。

冯晓容（1986—），男，硕士，助理研究员。

多方案分析（Analysis of Alternatives， AoA）是针对指定的某个或某些需求，研究各种可能方案的费用、效能和风险的客观分析活动。多方案分析是武器装备系统论证过程中的一个关键阶段，主要目的是确定装备备选方案是否具有完成任务的能力，其本质上是一个涉及多个利益相关者的多准则决策过程。

国内外学者的多方案分析方法研究可分为以下几个方面：一是框架研究。陈白雪分析了面向装备论证的多方案分析内涵，并从需求分析、可行性分析阶段和方案分析及优选三个阶段构建了面向装备论证的多方案分析基本框架［1］。KRESS和MORGAN针对装备论证多方案分析给出了具有广泛适用性的分析框架［2］。二是方法研究。国内学者采用的方法主要包括数据包络法［3-7］、博弈论［8］、粗糙集［9］、模糊综合评判［10］、协同论证［11］、层级分析法［12］。三是指标体系研究。蒋铁军针对舰船装备论证方案的综合评估问题，提出了一种较为系统而全面的综合评估方法，建立了论证方案的评价指标体系［13］。

根据研究现状的分析，目前的装备论证多方案分析方法在作战效能分析中，通常将装备固有能力作为其系统效能，没有充分考虑装备的可用性和任务成功性，而可用度和任务成功度与装备可靠性（Reliability， R）、维修性（Maintainability， M）和保障性（Supportability， S）密切相关。因此，需要在多方案分析中充分考虑RMS因素。本文首先介绍装备论证过程中的多方案分析框架，并给出装备论证多方案指标体系，然后介绍对多方案分析具有影响的RMS和费用的因素及其量化模型，最后给出基于数据包络法的多方案分析模型及应用示例，说明方法的可行性和有效性。

1 装备论证多方案分析

多方案分析是对所提出的装备备选方案的效能、费用和风险的分析比较，以解决作战能力上的差距和不足。装备论证过程中的多方案分析基本框架如图1所示。因为系统效能和费用是装备研制、采购及维修保障决策的重要目标或制约条件，所以，多方案分析通常采用效用-费用分析框架，主要包括作战效能分析和费用分析两部分。

以上研究从资源约束、评价函数、任务时序等不同角度对CMTAP进行改进，但仍存在异构型无人机及不同类型目标间的差异刻画较为简单的问题，同时，模型中目标的设定规模往往较小，难以充分体现多机相较于单机执行多任务目标时的效率优势。且由于多机协同任务分配的NP-Hard特性，随着目标规模的增加，传统启发式算法搜索结果质量差，易陷入局部最优的缺陷将愈发明显［16］。

2020年，学者Khishe通过模拟黑猩猩捕猎行为，提出一种新型启发式算法黑猩猩算法（Chimp Optimization Algorithm， ChOA）［17］。ChOA根据个体能力的差异将黑猩猩群体划分为不同角色，进而使用不同的搜索策略使得整个群体在求解空间中快速寻优，具有原理简单，搜索效率高，擅长高维问题求解的特点，因此在异构多无人机协同任务分配这一典型的高维优化问题求解方面具有很大的应用潜力。同时，由于算法提出较晚，ChOA在很多方面仍有很大的改进空间，如在求解复杂多维目标函数时依然存在局部易收敛、全局与局部搜索不平衡的问题。

基于上述分析，本文使用CMTAP对异构无人机执行地面多类型固定目标的场景进行刻画，使用改进黑猩猩算法（Modified Chimp Optimization Algorithm， MChOA）进行求解。在模型构建中，将任务收益、威胁代价、总航程三个优化目标按权重纳入评价函数，以更好地反映执行不同任务分配方案时的总收益、危险系数和能耗三项指标。

1 异构多无人机协同任务分配模型

本节将设计一个可更好刻画异构无人机执行地面多类型固定目标场景的CMTAP。为更好地体现差异性，本文首先使用六元组对每一架无人机及每一个目标的多方面信息进行设定，然后，设置了相应的约束条件以确保任务分配方案的可行性，最后，设计了评价函数以衡量任务分配方案的优劣。

1.1 问题描述

CMTAP中，可将任务分配问题用一个四元组｛E，V，T，C｝表示，其中，E为任务区域，V为无人机集合，T为任务集合，C为约束集合，通过对四元组集合内的元素进行调整以刻画不同的任务需求。

无人机集合为V=｛V1，V2，…，VNV｝，本文为更好地体现无人机的异构性，设定无人机Vi均可由六元组〈LVi，SVi，RVi，AVi，Pi，WVi〉进行描述，其中，LVi=｛xVi，yVi｝为无人机Vi的当前位置坐标;SVi为无人机Vi的类型，SVi=1表示可实施打击的战斗无人机，SVi=2表示可实施侦测的侦察无人机，SVi=3表示可实施侦测和打击的多功能无人机;RVi为无人机Vi的侦察能力;AVi为无人机Vi的攻击能力;Pi为无人机Vi携带的武器数目;WVi为无人机Vi的价值。

目标集合为T=｛T1，T2，…，TN｝，设定目标Tj均可由六元组〈LTj，Dj，Sj，Rj，Aj，Wj〉表示，其中，LTj=｛xTj，yTj｝为目标Tj的位置坐标;Dj为目标Tj的防空威胁;Sj为目标Tj的类型，Sj=1表示打击目标，Sj=2表示侦察目标;Rj为目标Tj的侦察需求;Aj为目标Tj的攻击需求;Wi为目标Tj的价值。

在确保模型有效性的前提下，为降低求解难度，本文假设模型中所有目标的地理坐标已通过前期各种侦察手段得到，所有无人机在执行任务过程中为定高匀速直线飞行，任务执行完毕后返回原出发位置。

1.2 约束条件

在构建CMTAP时，通常需要设置约束条件以确保任务的可行性。本文约束设置环节主要考虑无人机资源约束和任务协同约束，其中无人机资源约束包含最大航程约束和载弹量约束，具体内容如下：

1）最大航程约束。为确保无人机的安全，各架无人机执行任务期间的总飞行距离应小于该无人机的最大航程。无人机Vi所执行任务序列为SeqVi=｛TVij1，TVij2，…，TVijN｝，dist（TVik，TVik+1）表示无人机Vi从第k个任务到第k+1个任务的飞行距离，即

dist（LVi，TVij1）+dist（TVijN，LVi）+∑TVik ∈SeqVidist（TVik，TVik+1）≤max distVi （1）

2）载弹量约束。受载荷限制，无人机只能携带一定数量的导弹。因此，单个无人机执行任务使用的导弹数目不能高于其携带的武器数目。CVi为无人机Vi任务序列中攻击目标的数量，即

CVi≤Pi （2）

3）任务协同约束。为了避免任务重复执行和无人机空置问题的发生，要求目标集合里的每个目标只能被执行一次，无人机集合里的每架无人机至少分配一个目标，且无人机具有执行对应分配目标的能力。

1.3 评价函数

无人机协同多任务分配的原则是在满足约束的条件下，实现整体作战效率最高的同时所付出的代价最小，而多无人机执行所有任务的任务收益、威胁代价和总航程是评价任务分配方案质量的重要指标。因此，本文衡量无人机协同多任务分配方案优劣的评价函数由以下三部分组成：

1）任务收益。rewardVi（Tj）表示无人机Vi完成目标Tj的任务收益，其值由目标价值、目标需求和无人机能力共同决定，在任务分配中的作用是促使高价值目标和高需求目标倾向于分配给能力强的无人机执行，以提升重点目标的任务执行成功率，对侦察目标和打击目标的任务收益计算分别为：

rewardVi（Tj）=RVi*Rj*Wj （3）

rewardVi（Tj）=AVi*Aj*Wj （4）

2）威胁代价。riskVi（Tj）表示无人机Vi完成目标Tj所承担的风险代价，其值由目标的防空威胁和无人机的价值共同决定，其在任务分配中的作用是促使高价值无人机倾向于执行较安全的目标，以减小无人机被防空火力击落造成损失，其表达式如下所示：

riskVi（Tj）=Dj*WVi （5）

3）无人机航程。distVi（Tj）表示无人机Vi前往目标Tj的航程代价，所有无人机的总航程之和反映了当前任务分配的资源消耗情况，其在任务分配中的作用是减少多无人机执行任务的资源消耗，其表达式如下所示：

distVi（Tj）=（xVi-xTj）2+（yVi-yTj）2 （6）

根据以上优化指标，得到无人机Vi执行目标Tj的任务评价函数如下：

JVi（Tj）=w1*rewardVi（Tj）+w2*riskVi（Tj）+w3*distVi（Tj） （7）

其中，w1、w2、w3分别为以上三项指标的权重值，且w1+w2+w3=1，具体数值由指挥中心根据任务需要设定，计算时需要确保各指标量纲统一。

2 基于改进黑猩猩算法的多机协同任务分配算法

对异构多无人机协同任务分配的求解本质上是多约束下的多目标优化求解问题，为此本节采用了基于改进黑猩猩算法的多机协同任务分配算法。

2.1 标准黑猩猩算法

ChOA可由以下三个方面描述：

1）等级制度。ChOA模拟自然界中黑猩猩群体的等级系统与捕猎机制，在完成种群初始化后，依据适应度的大小将群体划分为两层：领导层和基础层。领导层中包括攻击者、追逐者、障碍者和驱赶者四只黑猩猩，他们依次是本次计算中适应度最好的四个解。其他黑猩猩统一作为基础层，依据与领导层黑猩猩的距离来更新自身位置。在黑猩猩群体不断迭代的过程中，基础层的黑猩猩也会不断择优替补以更新领导层。

2）驱赶、包围猎物。黑猩猩驱赶、包围猎物的数学模型为：

d=|C·xprey（t）-m·xchimp（t）| （8）

xchimp（t+1）=xprey（t）-A·d （9）

其中，t为当前迭代次数，d为黑猩猩距猎物的距离，A、C、m为系数向量，xprey（t）为猎物位置，xchimp（t）为当前黑猩猩所在位置。A、C、m由式（10）～（12）计算得出。

A=2·f·r1-f （10）

C=2·r2 （11）

m=chaotic_value （12）

其中，f为收敛因子，其值从2.5随迭代过程非线性减小至0，算法通过不同类型的黑猩猩采用不同策略更新f的方式，赋予了黑猩猩群体用多种方式搜索解空间的能力。A为［-f，f］之间的随机数，当|A|>1时，黑猩猩远离猎物开展全局搜索，反之，靠近猎物进行局部搜索。r1和r2是［0，1］间的随机向量。m为混沌映射，代表黑猩猩在捕猎过程中抢食行为的影响。

3）攻击猎物。在捕猎过程中，位于领导层的黑猩猩能够更好地了解猎物的所在位置，其他黑猩猩依据领导层黑猩猩的位置更新自身位置，最后由攻击者黑猩猩完成捕猎。这种行为可用数学公式（13）～（15）表示：

dAttacker=|C1·xAttacker-m1·x|dBarrier=|C2·xBarrier-m2·x|dChaser=|C3·xChaser-m3·x|dDriver=|C4·xDriver-m4·x| （13）

x1=xAttacker-A1·dAttackerx2=xBarrier-A2·dBarrierx3=xChaser-A3·dChaserx4=xDriver-A4·dDriver （14）

x（t+1）=（x1+x2+x3+x4）／4 （15）

在捕猎的最后阶段，食物的吸引力会导致黑猩猩暂时忘记它们的捕猎责任，试图在混乱中获取食物。ChOA使用混沌映射对这种抢食行为进行描述，并设定在优化过程中有50％的概率在正常位置和混沌位置之间选择，这种行为有助于避免算法陷入局部最优和求解高维问题，是区分ChOA与其他启发式算法最重要的因素。抢食行为可用数学公式（16）表示：

xchimp（t+1）=xprey（t）-A×di，μ<0.5chaotic_value，μ≥0.5 （16）

其中，μ是［0，1］间的随机值。

2.2 混沌反向学习策略的种群初始化

初始化阶段，初始种群的生成质量对启发式算法的求解速度和最终结果有很大影响。ChOA采用的纯随机初始化方式易造成黑猩猩初始种群分布过于集中或分散，导致算法局部收敛和搜索效率低下等缺陷。为提升算法的全局寻优性能，在保证随机性的同时应使初始种群尽可能均匀分布。为此，本文使用混沌反向学习策略完成MChOA的种群初始化。

混沌映射生成的混沌序列是一种由确定性规则产生的随机序列，该序列能够在一定范围内根据规则遍历解空间而不发生重复。使用混沌映射取代纯随机的方式完成初始化环节，结合其遍历性和非重复性的特点，可提升黑猩猩初始种群分布的多样性，改善算法的全局寻优能力。

本文首先引入Tent混沌映射，其形式如下：

zk+1=zk／β，zk∈（0，β］（1-zk）／（1-β），zk∈（β，1］ （17）

该映射结构简单，在[0，1]区间内产生的混沌序列分布较均匀，设β取值0.7，此时映射具有较好的混沌特性。

其次，在使用混沌映射生成初始种群的基础上，ChOA通过领导层四只黑猩猩（历次计算中适应度最好的四个解）的分布来估计猎物的位置，进而影响种群中个体的迭代方向，初始种群中个体的分布距全局最优解越近，则算法的寻优速度越快。由于种群中的个体黑猩猩和其反向个体更靠近全局最优解的概率是50％，因此，在MChOA的种群初始化中考虑每个个体的反向个体，选择更靠近全局最优解的个体黑猩猩组成更高质量的初始种群，通过减少低效搜索的次数进一步加快算法的寻优进程。数学表达式如下所示：

X′（1）=lb+ub-X（1）X（1）=X（1）， J（1）>J′（1）X′（1）， J（1）<J′（1） （18）

式中，ub、lb是种群X的上下界，X（1）是种群该次迭代中的第一个粒子。

2.3 抢食行为动态调整策略

ChOA在收敛阶段设置了抢食行为，通过以固定跳变概率μ在正常位置迭代和混沌位置迭代间切换的方式达到跳出局部最优的目的。但是，由于收敛阶段不同适应度的个体陷入局部最优的风险并不相同，如能对不同风险陷入局部最优的个体施加相对应的跳变概率，可进一步提高算法在收敛阶段的搜索性能，为此本文引入抢食行为动态调整策略。

启发式算法收敛阶段陷入局部最优解，往往是因为种群中个体随迭代逐渐聚集到当前最优解（非全局最优解）。在迭代中，适应度值越高的个体陷入局部最优解的风险越大。在收敛阶段，可将适应度值较高个体的跳变概率增大，使其更多地担负寻找更优解的责任，增强其规避局部最优的能力。同时，由于黑猩猩算法记录的是历史最佳四个解并将其定义为领导层黑猩猩，因此，即使适当增大适应度值较高个体的跳变概率，在未寻找到更优解的情况下，也不影响种群主体向最优解靠拢的趋势。对适应度值较低的个体，通过降低其跳变概率，可使其按照正常模式更新并尽快向历史最优解靠拢，若此时历史最优解位于全局最优解附近，基于该模式下A、C、m系数本身的随机性，可通过种群在历史最优解周围更密集地探索提升全局最优解的发现概率。

假设经过k次迭代，当前粒子i的适应度为Jk（i），种群X的平均适应度为Jkavg，种群X中高于平均适应度的所有粒子的平均适应度为Jkabove_avg，种群X中低于平均适应度的所有粒子的平均适应度为Jklow_avg，种群X的最大适应度为JkAttacker，种群X的最低适应度为Jkmin，则将跳变概率μ按如下方式设置：

1）Jk（i）>Jkabove_avg 时

此时粒子的适应度值处于较高水平，为此应在合理区间内加大该粒子的跳变概率μ，以减小领导层黑猩猩的影响，从而增强该粒子的全局寻优能力，防止陷入局部最优。数学表达式如下所示：

μ=μavg+（Jk（i）-Jkabove_avg）（μmax-μmin）JkAttacker-Jkmin （19）

2）Jklow_avg <Jk（i）<Jkabove_avg 时

当粒子适应度值介于中间值时，粒子抢食行为跳变概率μ设置为固定值，数学表达式如下所示：

μ=0.5 （20）

3）Jk（i）<Jklow_avg 时

此时粒子的适应度值较低，应减小该粒子的跳变概率μ，以增大领导层黑猩猩对其下次位置更新的影响。数学表达式如下所示：

μ=μmin-（Jklow_avg-Jk（i））（μmax-μmin）JkAttacker-Jkmin （21）

3 仿真实验及分析

3.1 仿真参数设置

本次实验采用Windows 11操作系统，仿真平台使用Matlab R2020a。设定任务区域为100 km*100 km，任务区域内目标为随机生成。

为进一步验证本文提出的MChOA在多无人机协同任务分配中的性能，使用经典启发式算法——遗传算法（Genetic Algorithm， GA）［18］、新型启发式算法——灰狼优化算法（Grey Wolf Optimizer， GWO）［19］以及ChOA作为对照组，算法的种群规模均设置为50，迭代次数为200，其他各项初始参数如表1所示。本文CMTAP评价函数中的三项指标权重值w1、w2、w3分别设置为0.6、0.3、0.1。

3.2 仿真结果及分析

为减少随机因素的影响，确保对比结果的准确性，各算法均重复运行20次，对比实验的结果以本文CMTAP的评价函数作为衡量指标。

1）UAV数量为6，目标数量为20

UAV和目标的设定如表2和表3所示。MChOA所得最佳任务分配方案如表4所示，该方案满足CMTAP中各约束条件，表明该异构多无人机协同任务分配方案的结果符合实验想定，具备可行性。

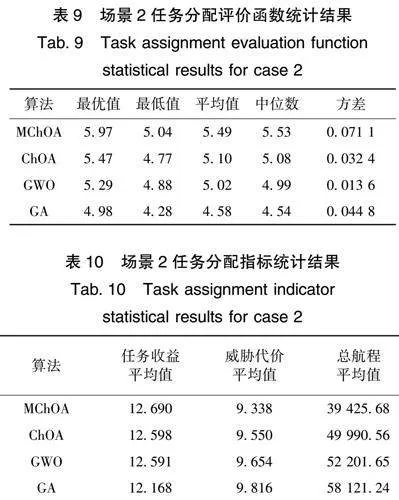
从表5的统计结果可以得出，在符合CMTAP约束的要求下，MChOA所得任务分配方案的评价函数值在最优值、最低值、平均值和中位数四项指标中均取得了最好的结果。相较于ChOA、MChOA的最优值、最低值、平均值、中位数分别提升了3.69％、 7.46％、7.66％、8.03％，这是因为抢食行为动态调整策略的引入使得MChOA具有更强的全局搜索能力，有效避免了陷入局部最优;MChOA的方差指标相较ChOA减小了30.89％，表明算法具有更好的收敛性，这是因为初始化阶段的混沌反向学习策略使得初始种群分布更加均匀，一定程度上减少了启发式算法的随机性对最终结果的影响。

为进一步探究评价函数值在衡量无人机集群执行任务分配方案中的实际影响，对比各算法20次仿真中评价函数加权前的各指标，结果如表6、图1和图2所示。从表6可以看出，MChOA之所以在评价函数中获得了最好的结果，是因为其所得任务分配方案在保持较高任务收益和较低威胁代价的同时，无人机总航程大幅度降低，其总航程平均值相较ChOA、GWO、GA分别降低了22.6％、37.4％、43.4％。在图1和图2任务分配方案的指标分布中也可以看出，MChOA的历次任务分配方案在保持了较高任务收益值和较低威胁代价的同时，在总航程代价方面始终分布在较低区域。

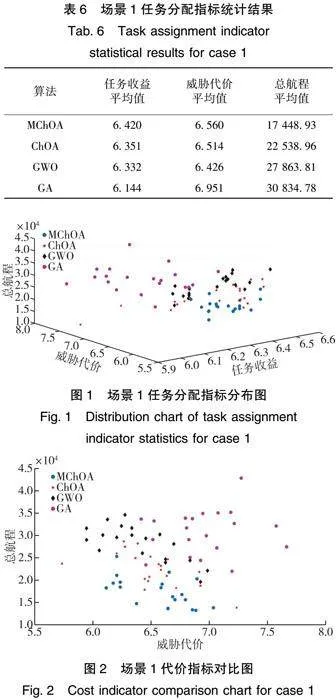
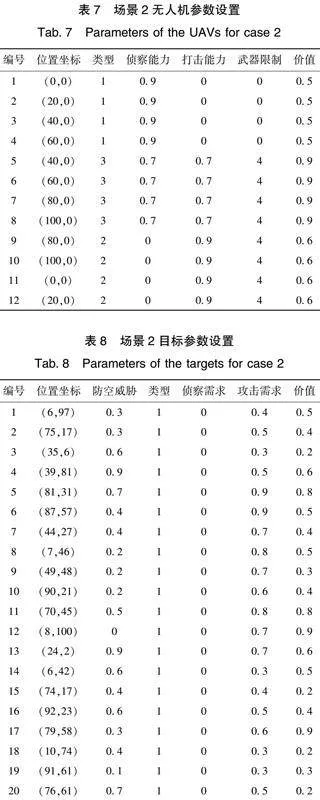
2）UAV数量为12，目标数量为40

根据多机协同任务分配问题的NP-Hard特性，问题维度越高，寻找全局最优解的难度越大。为验证更高维度下MChOA的性能，将UAV和目标的数量规模扩充一倍，具体参数设定如表7和表8所示，各算法20次任务分配结果的评价函数统计如表9所示。可以看出，MChOA在最优值、最低值、平均值、中位数四个指标方面依旧取得了算法对比中的最好值，相较于ChOA，MChOA在最优值、最低值、平均值、中位数指标方面分别提升了9.14％、 5.66％、7.65％、8.86％，表明其在求解问题维度升高时依旧可以保持较好的寻优性能。此时，

高维问题下的全局最优解搜索难度加大导致MChOA的方差增加，但结合统计数据可以看出，ChOA及其他对比算法所得任务分配方案的最优值仍低于MChOA的平均值，表明方差指标增大并未影响MChOA给出的方案始终稳定在一个较高水平。

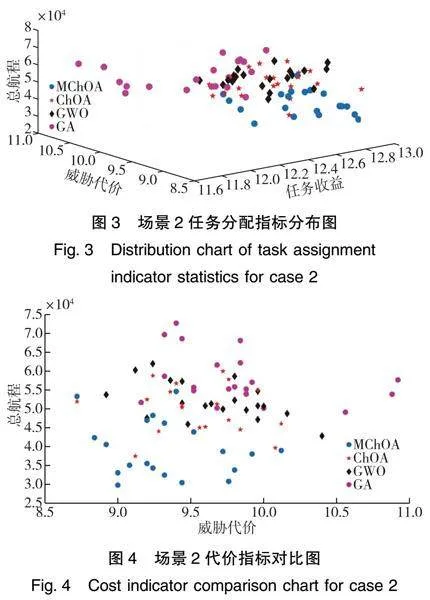
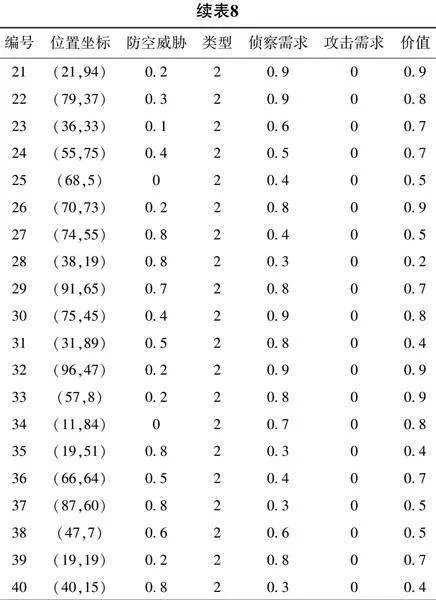
进一步对比各算法评价函数加权前的各指标，结合表10、图3和图4可知，MChOA所得20次任务分配方案在取得最高平均任务收益及最低平均威胁代价的基础上，总航程平均值相较ChOA、GWO、GA分别降低了21.1％、24.5％、32.2％，取得了高评价函数值，证明了MChOA所得任务分配方案的优越性。

4 结束语

本文利用CMTAP和MChOA解决了异构多无人机对地面多类型固定目标的协同任务分配问题。首先，通过对四元组内元素的设定完成模型构建，更好地体现了异构无人机、多类型目标间的差异性。其次，引入混沌反向学习策略和抢食行为动态调整策略对ChOA的初始化阶段和迭代阶段进行改进。两种不同规模下的仿真实验中，MChOA仿真结果的评价函数的最优值、最低值、平均值、中位数均取得了最好的结果，其所得任务分配方案在保持较高的任务收益和较低威胁代价的同时，相较于原算法，两种规模场景下的平均总航程分别降低了22.6％和21.1％，验证了算法的有效性。但本文在计算航路代价时使用了欧氏距离，在航路中间存在绕行障碍时可能导致预估误差较大，会影响任务分配方案的实际优化效果，下一步可在衡量航路代价时引入新的计算方式，以快速且更加准确地完成障碍环境下的航路代价预估。

参考文献：

[1] YANG W Z， XIN Y. Multi-UAV task assignment based on quantum genetic algorithm［J］. Journal of Physics： Conference Series， 2021， 1824（1）： 012 010.

［2］ 樊鹏辉， 宋国鹏， 孟博， 等. 多无人机协同作战应用研究［C］／／中国航天电子技术研究院科学技术委员会2020年学术年会论文集. 北京， 2020： 54-60.

FAN P H， SONG G P， MENG B， et al. Research on the application of multi-UAV cooperative operations［C］／／Proceedings of the 2020 Academic Annual Meeting of the Science and Technology Committee of the China Academy of Aerospace Electronics Technology.Beijing，2020：54-60.

［3］ 康瑞梦. 基于群智能算法的无人机群协同任务分配研究［D］. 成都：电子科技大学， 2023.

KANG R M. Research on the multi-UAV cooperative task assignment method based on the swarm intelligence algorithm［D］. Chengdu： University of Electronic Science and Technology of China， 2023.

［4］ 张力升， 郑明发， 钟海涛. 不确定环境下无人机多目标任务分配问题研究［J］. 计算机仿真， 2022， 39（9）： 68-73， 100.

ZHANG L S， ZHENG M F， ZHONG H T. Research on multi-target assignment of UAV under uncertain environment［J］. Computer Simulation， 2022， 39（9）： 68-73， 100.

［5］ 彭鹏菲，龚雪，姜俊，等.基于改进多维粒子群的多无人机任务分配方法［J］.兵器装备工程学报，2023，44（7）： 227-236.

PENG P F， GONG X， JIANG J， et al. An improved multi-dimensional particle swarm-based approach to multi-UAV mission assignment[J］. Journal of Ordnance Equipment Engineering， 2023，44（7）： 227-236.