基于学科融合的高中数学教学

《普通高中数学课程标准（2017年版2020年修订）》中强调，数学教学需要重视与学生生活以及其他学科的联系，重视培养学生运用数学知识解决实际问题的能力。本文以高中数学“直线和圆的位置关系”的教学为例，探讨如何在高中数学中融合少数民族文化。

一、高中数学融合人文学科可行性分析

学科融合是实现学生学科核心素养培养、知识迁移和创新应用的重要途径。在教学中，教师可以通过改革教材内容和教材呈现方式改进学生的原有认知结构变量，以达到迁移的目的。因此，在数学教学中，教师可以利用人文学科知识建立数学知识与现实生活的联系，在学生已有的生活认知基础上讲解数学知识，为学生创设情境，促使学生发现新知识与旧知识之间的联系，鼓励学生系统性学习，帮助学生构建清晰的知识网络。

二、高中数学学科融合教学“四阶段”

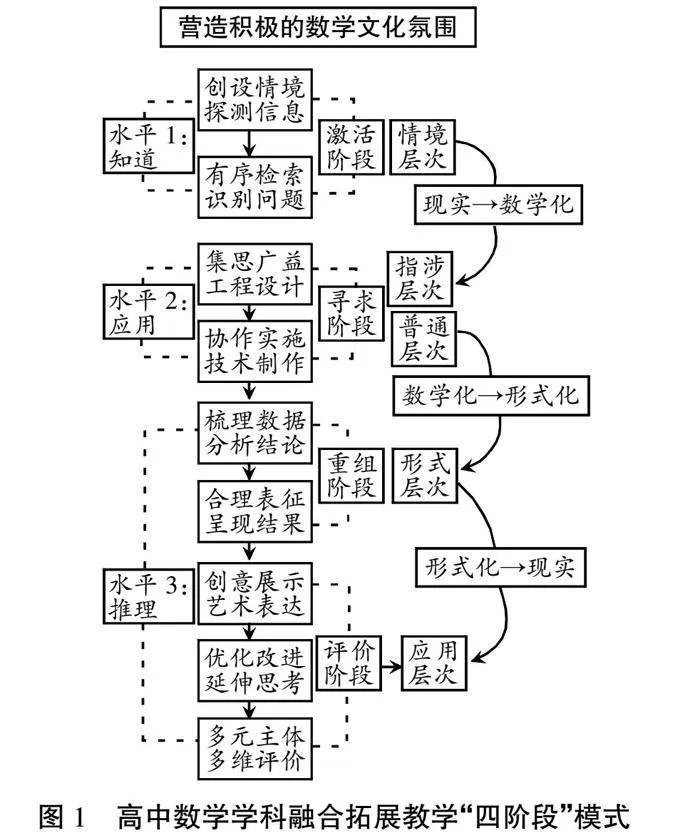
学科融合教学作为一种拓展型教学新范式，为学生联系真实生活情境、解决生活中遇到的问题提供了阶段性帮助，主要包括四个阶段（见图1）。

1.激活阶段。教师通过整合数学知识与人文科学中的实际情境，设计“情境创设，识别问题”的教学环节，创设数学学习情境。

2.寻求阶段。教师通过引导学生打开已有的认知结构，从已有的认知结构中连接数学知识，调动学生已有的知识，整体处于知识的应用水平。

3.重组阶段。在该阶段，教学主要涉及“梳理数据，分析结论”等学习环境，实现知识间存在的既有联系梳理。这部分知识的重组和应用层面要求，本质上指的是归纳和梳理已有的教学成果，实现教学容量和教学需求调整。

4.评价阶段。该阶段是对学生应用数学知识与其他学科融合的创意展示和艺术表达，综合考虑优化学生思维，改善和改良学生的多元主体，实现教学评价行为。在评价阶段，教师对学生知识的重组进行分析、整合和评估。学生的认知情况发展到具体的“推理应用”水平。

三、高中数学融合少数民族文化情境教学

少数民族文化与数学学科知识具有一定的联系，抓住少数民族文化与数学学科知识之间的联结点，将少数民族文化融入数学教学中，帮助学生在已有的对于少数民族文化了解的基础上创设学习数学的情境。布依铜鼓是布依文化中不可缺失的一部分，铜鼓整体呈现圆柱形结构，与骨架交错呈现了圆与直线的位置关系。基于此，以高中数学“直线与圆的位置关系”教学中融合布依族文化中的“布依铜鼓”文化知识为例，教师以一个引导者的角色进行教学，创设“布依铜鼓”文化背景的数学教学情境，以“四阶段”教学模式为基础，通过情境教学的方式引导学生自主探索“布依铜鼓”中直线与圆的位置关系。

【教学目标】

1.以布依族文化为背景，融合其他学科的文化知识，通过“布依铜鼓”创设教学情境，在具体的实物图形中展现圆和直线的位置关系，以真实情境引导学生了解三种位置关系，并且可以通过代数法判断三种位置关系。

2.以少数民族文化为背景，为学生创设学习数学的实际情境，通过融合跨学科知识，激发学生思维，从知识的联系中提升学生对知识的兴趣和探究动力。少数民族文化知识与数学专业知识相结合，让学生从生活实际中观察、总结数学规律以及培养直观思维和抽象思维，提升学生的数学核心素养。

3.通过设计的教学四阶段结合少数民族文化背景，提升学生的数学抽象、逻辑推理、直观想象以及数据分析和数学运算等数学核心素养，培养学生数学学习的自信心。

【教学过程】

1.课堂导入

★激活阶段

教师可以通过课堂提问的形式创设学习情境，引入课堂学习新知识。

师：班上有哪些同学是布依族的？有的话老师想采访一下你，你会你们民族的哪些乐器呢？或者你知道你们民族有哪些乐器吗？

通过问题，教师引导学生说出“布依铜鼓”这一文化背景，以“布依铜鼓”文化为背景，播放相关的视频和图片为学生创设新知的学习情境。

★寻求阶段

师：我国古代有很多乐器，一部分随着社会的发展而消失了，但是“布依铜鼓”是保存至今为数不多的乐器，它承载着布依族的少数民族文化流传至今。同学们，通过观察老师给的铜鼓图片说一下铜鼓的平面是哪一种几何图形。

生：圆。

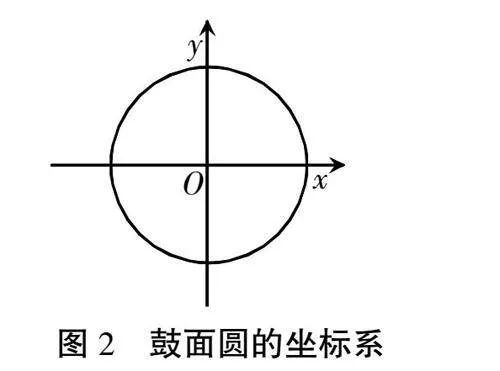
教师为学生展示目前最大的“布衣神鼓”图片，并且介绍铜鼓的高度及鼓面直径等数据，引导学生通过建立坐标系来写出铜鼓鼓面圆的两种形式的方程式。

师：观察图片上这个独一无二的“布衣铜鼓”，鼓面半径为55 cm，同学们可以写出该铜鼓的圆坐标方程吗？

★重组阶段

教师通过引导学生复习圆的标准方程知识，即圆的标准方程为（x-a）2+（y-b）2=r2，其中圆心为（a，b），r为半径。则圆的标准方程为x2+y2+Dx+Ey+F=0，其中D2+E2-4F>0，则圆心为（-，-）；半径为r=。

在教师带领学生复习之后，学生通过思考和观察，以鼓面的中心为原点O（0，0）建立坐标系（如图2所示），圆的半径r=55 cm，则可以写出圆的一般方程和标准方程：

（1）标准方程：x2+y2=3025

（2）一般方程：x2+y2-3025=0

★评价阶段

创设“生生互评”和“师生评价”结合的实践讨论活动，学生对彼此写出的一般方程和标准方程进行互评，并且在课堂上阐述学生在写方程时遇到的问题。最后由教师进行总结评价，深化学生对所学知识的印象。

（设计意图：以“布衣铜鼓”文化背景的相关视频、图片和问题导入新课，让学生在欣赏布依族音乐文化的同时，激发学生的学习兴趣。）

2.直线与圆的位置关系探究

★“激活+寻求”阶段

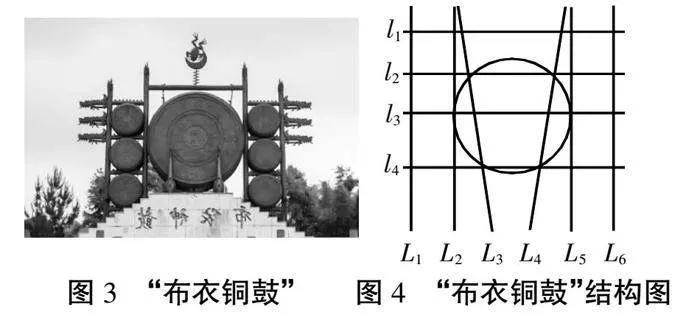
通过课程导入，学生对所学新知有了初步的了解和认识，教师通过明确学生的学习任务和目标，让学生运用代数法、几何总结直线和圆的位置关系，并且判断圆和直线的位置关系。教师通过展示“布衣铜鼓”的图片（如图3所示），将图片中布衣铜鼓的骨架看为直线、主鼓鼓面直观想象为圆（如图4所示），并引导学生回答问题：

问题1：图4中的鼓面和10条吊绳（l1、l2、l3、l4、L1、L2、L3、L4、L5、L6）有什么样的位置关系？

★重组阶段

通过观察图4，学生回答：

直线L1、L6和l1与圆相离，无公共点；L2、L5与圆相切只有一个公共点；l2、l4、L3、L4与圆相交有两个公共点。

★评价阶段

教师对学生阐述的观点进行评价，对学生提供及时性反馈，帮助学生构建正确的知识结构。

（设计意图：以“布衣铜鼓”作为吸引学生探究所学知识的研究对象，引导学生判断两者之间的关系。）

3.直线和圆的位置关系判断

★激活阶段

教师播放视频资料，并向学生抛出问题，询问学生使用什么方法判断直线和圆的位置关系，并提出只给出直线和圆的方程，学生如何通过圆和直线方程判断两者之间的关系。

★寻求阶段

教师引导学生通过代数法来完成上面的知识梳理，让学生通过分组完成问题，分组在讲台上向同学们展示他们的演算过程，以此提升学生的交流能力以及学习自信心。

教师在引导学生代数法的过程中，将图4中的l3作为x轴，L2作为y轴建立直角坐标系，由此可以得出圆C的方程：（x-2）2+y2=4

并且创设问题情境：布依族为了节日喜庆，布依族人民想在铜鼓鼓架上挂一条红绸，设定红绸装扮的直线l的方程为2x-y-2=0，请大家判断二者的位置关系，若是两者相交，求出交点坐标。

★重组阶段

学生分组讨论之后，小组推选代表到讲台上展示他们的演算过程，A组学生的验算过程如下：

∵圆C（2，0），半径r=2，圆心到直线的距离：d==<2

∴直线和圆相交

则联立方程组：（x-2）2+y2=42x-y-2=0

得5x2-12x+4=0

解得这两个公共点的坐标分别是：A（2，2），B（，）。

★评价阶段

教师通过对小组代表分享的验算过程进行评价，提供学生积极的正向反馈，以此激发学生积极思考，勇于表达自我、敢于挑战新知的勇气和积极性。

（设计意图：在数学学习中融入对少数民族文化的探究，引导学生针对数学知识展开自主探究和讨论，让学生在题目讲解过程中以运输铜鼓为背景，了解数学来源于生活。）

【课后作业】

问题1：以O（0，0）为圆心的圆与直线4x+3y-35=0相切，计算圆的方程。

问题2：判断直线3x+4y+2=0和圆x2+y2-2x=0的位置关系。

问题3：已知直线与圆交于A，B两点，过A作l的垂线与x轴交于C，过B作l的垂线与x轴交于D，若AB=2，则CD= 。

（设计意图：通过开放性习题的设置，鼓励学生应用本节课的知识，实现数学知识的迁移和提升。）

（作者单位：广西柳州铁一中学）

编辑：温雪莲