挖掘试题条件·关注图形特征·探寻解题路径

摘 要：解决几何问题时需要挖掘试题条件、关注图形特征、关联核心知识. 参照波利亚解题四步法，重点探寻如何抓住图形特征，多角度分析试题；总结如何挖掘条件，理解题目；关注图形特征，拟订方案；回顾反思，总结提升.

关键词：波利亚解题四步法；解法探寻；图形特征；关联分析

中图分类号：G633.6 文献标识码：A 文章编号：1673-8284（2024）09-0059-06

引用格式：王静. 挖掘试题条件·关注图形特征·探寻解题路径：以一道中考几何试题为例［J］. 中国数学教育（初中版），2024（9）：59-64.

《义务教育数学课程标准（2022年版）》（以下简称《标准》）指出，要组织学生经历图形的分析与比较的过程，引导学生学会关注图形的共性与区别，理解几何问题的本质. 在教学中，教师要引导学生剖析几何图形的特征，根据特征挖掘、筛选、重组、关联条件，并抓住未知元素特征，联想核心知识，探索解题路径. 实际上，将一道试题分析透彻有利于培养学生分析问题和解决问题的能力. 以2023年中考江苏南京卷第16题为例，借助波利亚解题四步法，搭建已知与未知的桥梁，探索该题的解题路径.

一、试题呈现与分析

题目 如图1，在菱形纸片ABCD中，点E在边AB上，将纸片沿CE折叠，点B落在点B′处，[CB′⊥][AD]，垂足为点F，若CF = 4 cm，FB′ = 1 cm，则BE的长为___________.（设EB′与边AD交于点N.）

1. 素养分析

该题是试卷中填空题的压轴题，是在菱形的基础上进行翻折变换形成的图形，题干简洁，图形优美，其中蕴含的知识点较多. 试题考查了勾股定理，相似三角形的性质与判定，平行四边形、矩形的性质与判定，菱形的性质，平行线分线段成比例的基本事实，一次函数的相关知识，方程（组）等知识点，同时，考查了空间观念、抽象能力、几何直观、推理能力、运算能力等数学核心素养. 解决该题，要用数学的眼光观察问题，即从复杂的图形中抽象出基本图形，对基本图形进行条件分析、筛选、重组后进行条件的再发现、再创造. 同时，要用数学的思维思考问题，即抓住图形特征拟订方案，确定合理的解题路径.

该题适用于九年级二轮几何专题复习. 通过对该题的教学，能够帮助学生打通几何知识的脉络，使知识网络化、系统化，提高学生的综合分析能力，同时培养学生从数学角度、用数学思维进行问题求解，逐步养成有条理思考的思维品质.

2. 条件分析

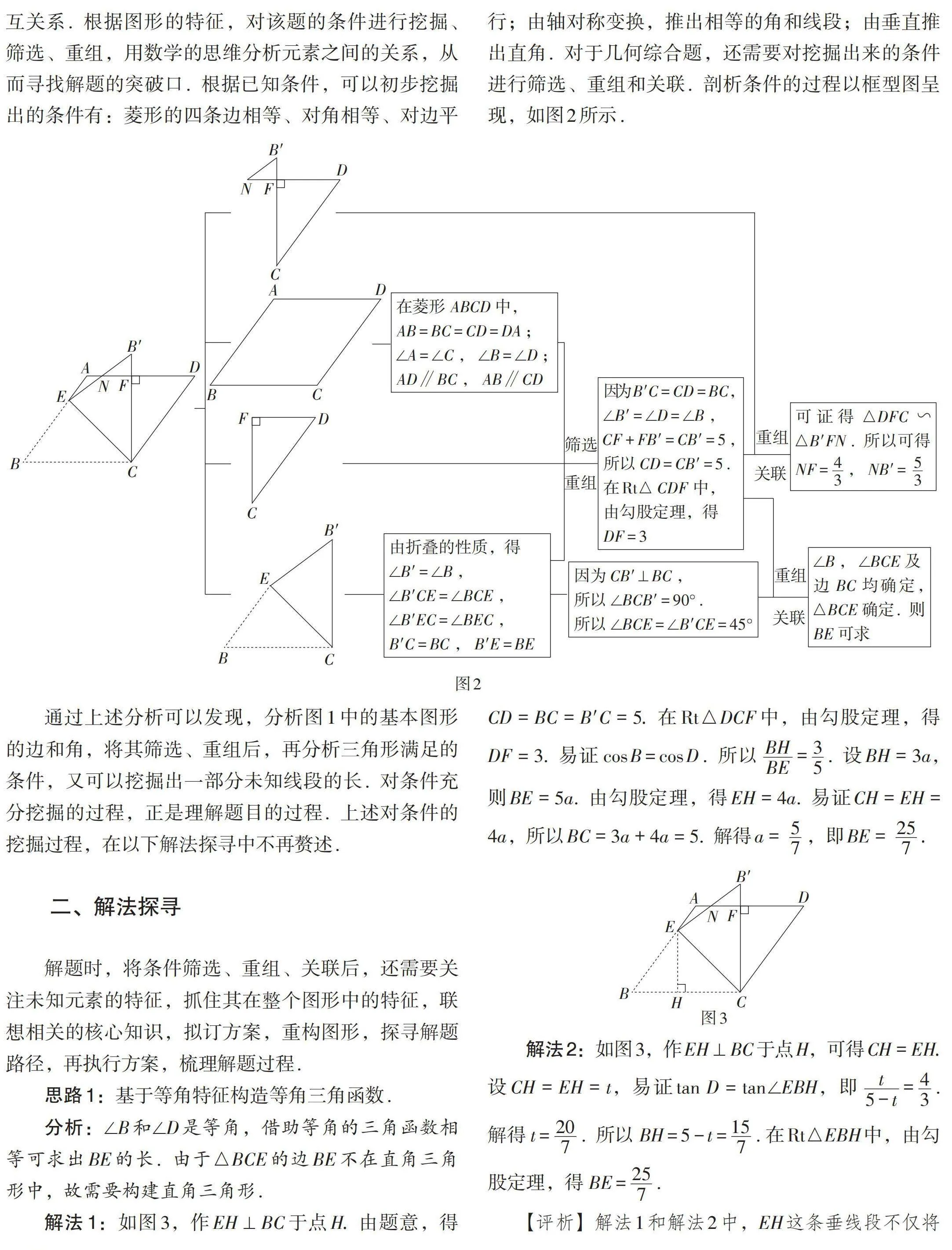
《标准》指出，要认识图形变化的基本特征，体会运动前后图形的变与不变，关注图形的基本性质和相互关系. 根据图形的特征，对该题的条件进行挖掘、筛选、重组，用数学的思维分析元素之间的关系，从而寻找解题的突破口. 根据已知条件，可以初步挖掘出的条件有：菱形的四条边相等、对角相等、对边平行；由轴对称变换，推出相等的角和线段；由垂直推出直角. 对于几何综合题，还需要对挖掘出来的条件进行筛选、重组和关联. 剖析条件的过程以框型图呈现，如图2所示.

通过上述分析可以发现，分析图1中的基本图形的边和角，将其筛选、重组后，再分析三角形满足的条件，又可以挖掘出一部分未知线段的长. 对条件充分挖掘的过程，正是理解题目的过程. 上述对条件的挖掘过程，在以下解法探寻中不再赘述.

二、解法探寻

解题时，将条件筛选、重组、关联后，还需要关注未知元素的特征，抓住其在整个图形中的特征，联想相关的核心知识，拟订方案，重构图形，探寻解题路径，再执行方案，梳理解题过程.

思路1：基于等角特征构造等角三角函数.

分析：∠B和∠D是等角，借助等角的三角函数相等可求出BE的长. 由于△BCE的边BE不在直角三角形中，故需要构建直角三角形.

解法1：如图3，作EH ⊥ BC于点H. 由题意，得CD = BC = B′C = 5. 在Rt△DCF中，由勾股定理，得DF = 3. 易证[cosB=cosD]. 所以[BHBE=35]. 设BH = 3a，则BE = 5a. 由勾股定理，得EH = 4a. 易证CH = EH = 4a，所以BC = 3a + 4a = 5. 解得a = [57]，即BE = [257].

解法2：如图3，作EH ⊥ BC于点H，可得CH = EH. 设CH = EH = t，易证tan D = tan∠EBH，即[t5-t=43]. 解得[t=207]. 所以[BH=5-t=157]. 在Rt△EBH中，由勾股定理，得[BE=257].

【评析】解法1和解法2中，EH这条垂线段不仅将∠B置于直角三角形中，更充分利用了“∠BCE = 45°”这个条件，产生共有直角边EH的两个直角三角形，且其中一个是等腰直角三角形（Rt△CEH）. 共边直角三角形是锐角三角函数这一章的基本图形. 解法1和解法2的不同之处是：解法1先利用等角三角函数得出线段之间的比，再按比例设未知数，最后利用线段之间的关系建立方程（[BH+CH=BC]）；解法2是先设未知数，并把相关线段用未知数表示，再利用等角三角函数建立方程. 两种解法都充分利用了等腰直角三角形CEH中“EH = CH”的条件. 也就是说，通过添加辅助线，又可以挖掘出新的角相等和线段相等，这个条件对该题的求解起着推动的作用.

思路2：基于边角特征“化斜为直”，构造相似三角形.

分析：要求线段的长度常用的方法就是构造相似三角形. 图1中Rt△CDF的三边长确定，联想构造与Rt△CDF相似的直角三角形. 因为BE是△BCE的一边，其中[∠BCE=45°]，基于线段BE和∠BCE的特征，故作[EH⊥CB]，将△BCE转化为有公共边的两个直角三角形，再利用相似三角形的对应边成比例，求出BE的长.

解法3：如图3，作[EH⊥CB]于点H，易证[EH=CH]. 设[EH=CH=t]，则[BH=5-t]. 易证[△BHE∽△DFC]. 所以[EHCF=BHDF]. 解得[t=207]. 下同解法2.

【评析】思路2与思路1的不同之处是：思路1利用锐角三角函数建立等量关系式求线段的长；思路2利用三角形相似建立等量关系式求线段的长. 两者本质是一样的，都是求线段的长的通法. 两种思路具有异曲同工之妙.

思路3：基于[AEBE]构造相似三角形.

分析：因为线段BE是线段AB的一部分，基于[AEBE]联想“X型”或“A型”相似三角形，利用相似三角形的对应边成比例求解BE的长.

解法4：如图4，延长DA交CE的延长线于点T，易证[TF=CF=4]. 因为[AF=AD-DF=2]，所以[AT=2]. 易证[△TEA∽△CEB]. 所以[ATBC=AEBE]，即[25=][5-BEBE]. 解得[BE=][257].

解法5：如图5，延长B′E交CB的延长线于点M，易证[△B′CM∽△DFC]. 易得[MC=203]，[BM=53]. 易证[△B′FN∽△DFC]. 易得[NF=43]. 所以[AN=23]. 易证[△AEN∽△BEM]. 所以[ANBM=AEBE]. 解得[BE=257].

解法6：如图6，延长CF交BA的延长线于点R，作[EM⊥CR]于点M. 易求得[AF=2]. 易证[△RFA∽][△CFD]. 易得[RF=83]，[RA=103]，[RC=203]，[RB=253]. 易证[CM=EM]. 设[CM=EM=a]，易证[△REM∽][△RBC]. 所以[EMBC=RMRC]. 解得[a=207]. 易求得[BE=257].

解法7：如图7，作[AQ⊥BC]于点Q，作[EP⊥B′C]于点P，AQ与EP相交于点M，易证四边形AMPF和四边形QMPC为矩形. 易知PE = PC，设PE = PC = a. 由已知，易证[△AEM∽△ABQ]. 所以[EMBQ=AMAQ]. 解得[a=207]. 所以FP = AM = [4-a =87]. 易证[AEBE=AMMQ]，解得[BE=257].

【评析】解法4和解法5分别是以△BCE和△AEN为基准构造“X型”相似三角形，解法6和解法7分别是以边BC和AB为基准在图形外和图形内构造“A型”相似三角形. 解法4、解法6和解法7在构造基本图形的同时，都产生了等腰直角三角形，借助等腰直角三角形腰相等的条件，使得求解过程顺利.

思路4：基于翻折特征等量代换构造相似三角形.

分析：图形翻折后，B′E是BE的对应边. 要求BE的长，可以等量转换为求B′E的长，而B′E又可以通过构造“A型”相似三角形求得.

解法8：如图8，作[EH⊥CB′]于点H，易证[EH=][CH]. 设[EH=CH=t]. 易证[△B′FN∽△DFC]，易求得[NF=43]. 易证[△B′NF∽△B′EH]. 所以[B′FB′H=NFEH]. 解得[t=207]. 所以[B′H=5-t =157]. 在Rt△B′EH中，由勾股定理，得[EB′=257].. 所以[BE=B′E=257].

【评析】将所求线段转换为等量线段进行求解是求线段长常用的方法. 此法可以拉近未知和已知的距离，已经挖掘出来的条件大部分集中在图形的右侧，等量转换后的线段EB′与已知条件间的联系更密切，可以构造以△B′NF为基准的“A型”相似三角形. 同时，也产生了共直角边EH的两个直角三角形，挖掘等腰直角三角形EHC的腰相等的条件，结合相似三角形，线段EB′可求，即线段BE可求.

思路5：基于平行特征补全平行四边形，构造相似三角形.

分析：因为菱形ABCD的对边平行，所以[BE∥CD]. 由BE为CD的平行线段，联想到以BC，BE为边构造平行四边形，通过求出此平行四边形的对边，进而求出BE的长.

解法9：如图9，作[EM∥BC]交B′C于点H. 易证[EH=HC]，四边形AEMD和四边形BEMC均为平行四边形. 设[EH=HC=a]，易证[△CHM∽△CFD]. 所以[CHCF=][HMFD]. 解得[a=207]. 所以[HF=4-a =87]. 易证[MDMC=][HFHC]. 解得[MC=257]. 所以[BE=257].

【评析】解法9构造平行四边形的方法也是将所求线段向图形的右侧平移转换，使未知和已知更靠拢. 与解法8的不同之处是，解法9是以△CFD为基准在图形内构造“A型”相似三角形.

思路6：基于图形确定性巧妙建系.

分析：线段BE的端点E是EB′与AB的交点，由于交点确定，联想构造平面直角坐标系，借助两个一次函数，求出交点E的坐标，进而求出线段BE的长度.

解法10：如图10，以点C为坐标原点，以边BC所在直线为x轴，以FC所在直线为y轴，建立平面直角坐标系，易证[△B′NF∽△DCF]. 易得[NF=43]. 易得点N，B′，A，B的坐标分别为[-43，4]，[0，5]，[-2，4]，[-5，0]. 易求直线AB的方程为[y=43x+][203]，直线NB′的方程为[y=34x+5]. 联立两直线方程，求得点E的坐标为[-207， 207]. 由勾股定理易求得[BE=257].

解法11：如图11，以点F为坐标原点，以边AD所在直线为x轴，以边B′C所在直线为y轴，建立平面直角坐标系. 同解法10，得[NF=43]. 易得点N，B′，A，B的坐标分别为[-43，0]，[0，1]，[-2，0]，[-5，-4]. 易求直线AB的方程为[y=43x+83]，直线NB′的方程为[y=34x+1]. 联立两直线方程，求得点E的坐标为[-207， -87]. 由勾股定理易求[BE=257].

【评析】解法10和解法11都采用了建系法. 此法思路简洁，是几何问题的代数解法，考查了数形结合思想. 建系的方法有很多，分别以点A，B，D，N，B′为坐标原点建系，均可以求出两条直线交点E的坐标，进而求出BE的长. 但是这几种建系方法的求解过程稍显烦琐.

三、教学启示

以上对试题的剖析过程遵循了波利亚的解题步骤. 波利亚的解题步骤是：（1）理解题目；（2）拟订方案；（3）执行方案；（4）回顾. 在这四个步骤中，“拟订方案”是解题的关键，“理解题目”是解题的前提.“拟订方案”往往是在不断深入理解题目中进行的，“执行方案”是解题的具体操作呈现，较前两个步骤容易一些，“回顾”是解题的必要步骤，检查结果的同时，更应该关注解题的回顾、提炼与拓展.

1. 挖掘条件，理解题目

对于一道几何题，要想快速破解，不仅要分析基本图形中的边、角元素，还要分析基本图形之间的关系，甚至在添加辅助线之后，还需要继续挖掘条件. 例如，该题的多种解法中，构造辅助线后产生了等腰直角三角形和共边直角三角形. 也就是说，对构图以后的图形，可以继续挖掘边和角的条件，条件越多，解题过程就越简洁. 有的学生抱怨做不出来题目，其实是对题目条件的挖掘不到位，找不到条件之间的联系，不能对已挖掘的条件进行再发现、再创造. 因此，只有充分挖掘题目条件，弄清题意，才能快速找到解题的突破口.

2. 关注特征，拟订方案

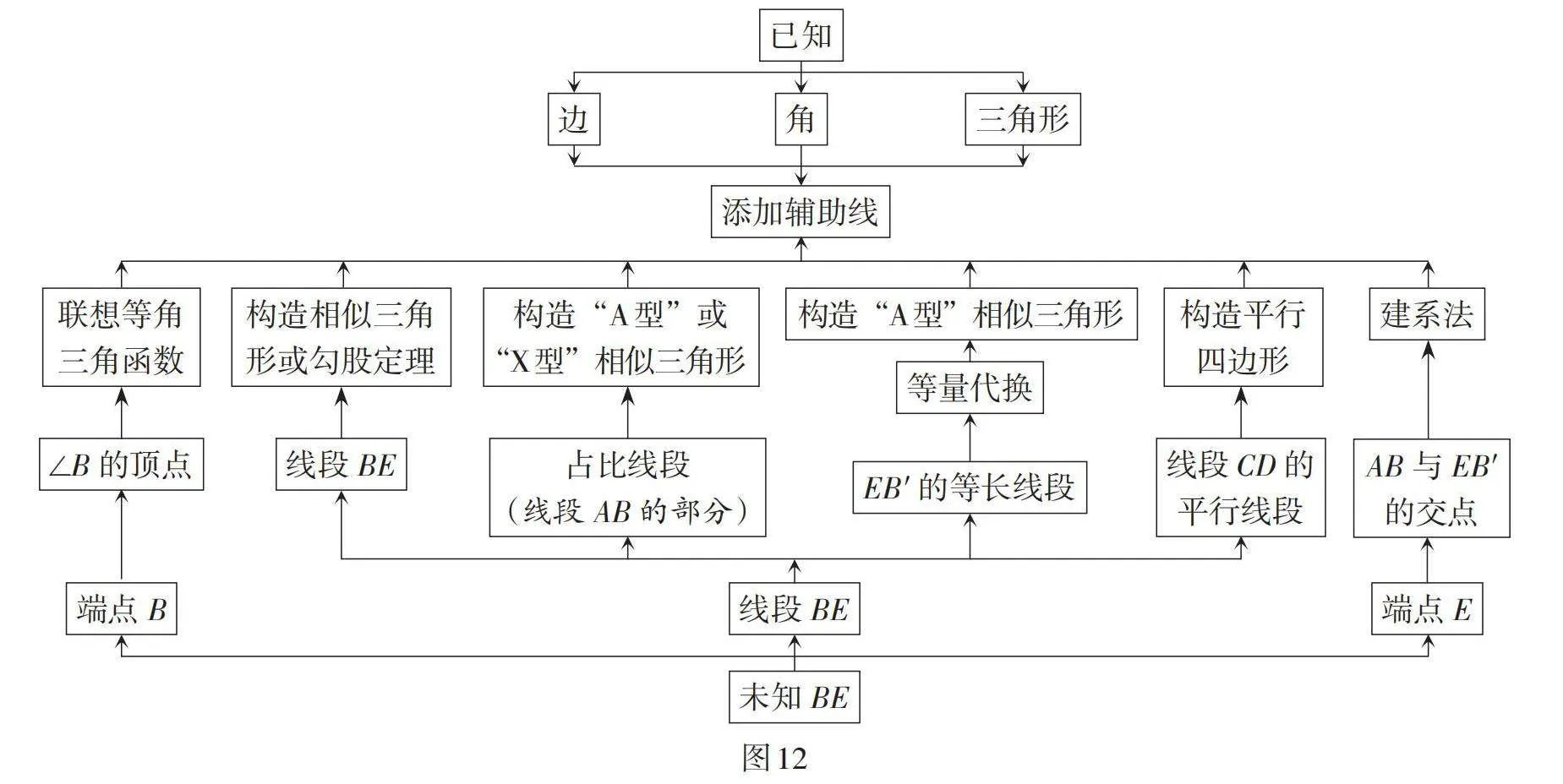
在解题时，首先要关注图形中未知元素的特征，如此题中的BE既是一条线段，更是占比线段（线段AB的一部分），线段的两个端点分别为两条线段的交点和某个角的顶点. 其次，剖析完元素的特征，针对相应的特征，就近联想采用何种解题思路，如该题的解法中关注等角特征、线段BE的位置特征、占比线段、平行线段、交点的确定性，分别采用了构建等角三角函数、“化斜为直”构造相似三角形、“A型”或“X型”相似三角形、平行四边形、平面直角坐标系等方法. 根据元素的特征，就近联想核心知识，探索解题思路，其本质就是拟订解题方案，这是解题的关键. 在探索解题思路的过程中，还要使未知尽可能向已知靠拢，如解法8和解法9的辅助线添加方法缩小了已知与未知的距离. 图12是该题多种解法的分析图，直观呈现了如何分析一道几何题，如何抓住未知元素特征拟订方案，打通未知与已知的联结通道. 通道打通后，执行方案则水到渠成.

3. 回顾反思，总结提升

波利亚曾说：如果你希望从自己的努力中取得最大的收获，就要从已经解决了的问题中找出那些对处理将来的问题可能有用的特征. 在解题教学中，并不是给出解法就意味着此题的解题过程结束，还需要回顾反思解法的异同、优劣，以及其中涉及的知识点、辅助线添加的切入点；还要思考是否有其他解法，以及解该题运用了什么思想方法，考查了什么核心素养. 在解法探析中，针对每一种解法进行了反思，只有不断回顾反思解题过程，在遇到难题时，才会知道如何分析、如何构造、如何关联核心知识，探索出解题的破解之道，才能提升学生分析问题和解决问题的能力. 通过引导学生归纳解题方法、技巧、规律和思想方法，能够促进知识向能力的转变，助力学生实现自我完善，争取达到“解一题，通一法，会一类，通一片”的效果.

解法探析中遵循“挖掘条件，理解题目—关注特征，拟订方案—整理思路，执行方案—回顾反思，总结提升”的解题流程，能让解题教学有章可循、有法可依.

参考文献：

［1］中华人民共和国教育部. 义务教育数学课程标准（2022年版）［M］. 北京：北京师范大学出版社，2022.

［2］波利亚. 怎样解题：数学思维的新方法［M］. 涂泓，冯承天，译. 上海：上海科技教育出版社，2011.

［3］杭秉全. 从“怎样解题”到“学会解题”［J］. 中学数学教学参考（中旬），2015（12）：23-26.

［4］波利亚. 数学的发现：对解题的理解、研究和讲授［M］. 刘景麟，曹之江，邹清莲，译. 北京：科学出版社，2006.

［5］李学军. 用本促真贴地前行：一道高二考题的思考历程［J］. 中学教研（数学），2016（4）：27-30.